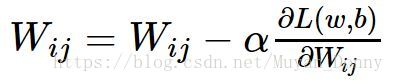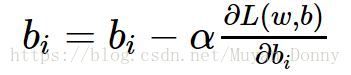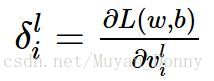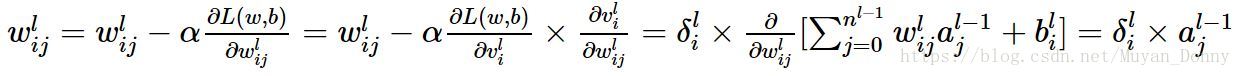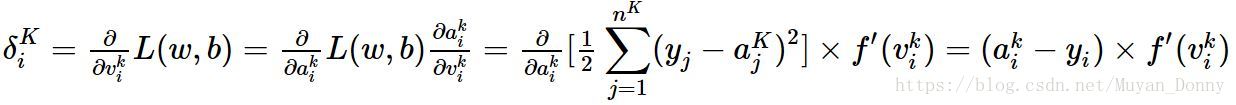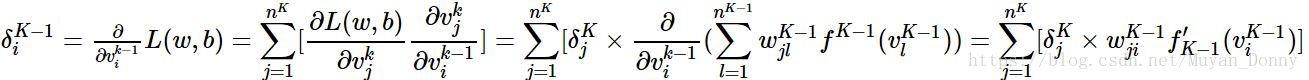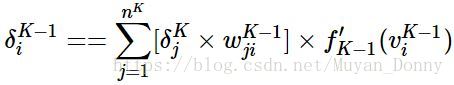梯度下降方法是常用的参数优化方法,经常被用在神经网络中的参数更新过程中。
神经网络中,将样本中的输入X和输出Y当做已知值(对于一个样本[X,Y],其中X和Y分别是标准的输入值和输出值,X输入到模型中计算得到Y,但是模型中的参数值我们并不知道,所以我们的做法是随机初始化模型的参数,不断更新迭代这些参数,使得模型的输出与Y接近),将连接权和偏置值当做自变量,误差L(损失函数的值)作为因变量。梯度下降的目的是找到全部连接权和偏置值在取何值的情况下误差最小。
经常有人把梯度下降的过程比作从山顶走到谷底,一次走多远比作“学习率”。那么,它 的数学表现形式是什么呢?
这就是梯度下降算法的迭代公式,当梯度下降为零时,w、b收敛,训练结束。
反向传播思想可以用来方便的求出损失函数对每个参数的导数,其基本原理是求导数时的链式法则。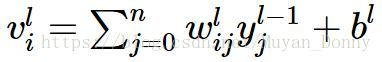
其中,Vil表示第l层第i个节点的值,yj(l-1)表示第(l-1)层第几个节点输出的值(也即激活值aj(l-1))
定义残差为:
则迭代公式根据链式法则可改写为 :
这两个公式写的都有点错误,前面两个等号内容是连接权和偏置值迭代的演算;后两个等号内容是损失函数对连接权和偏置值的偏导。
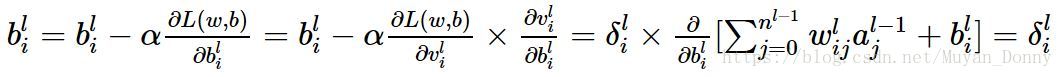
是表示第(l-1)层的第 j 个节点的激活值,即
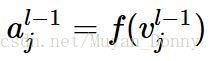
利用残差可以以统一的形式表示各层节点的连接权和偏置值的迭代公式。那么,各层节点处的残差是怎么计算的呢?
这就是反向传播算法设计的内容,反向传播过程的细节如下:
(1)随机初始化网络中各层的参数:连接权和偏置值,通常将它们随机初始化为均值为0、方差为0.01的随机数
(2)对输入数据进行前向计算,从输入层到输出层,依次计算每一层的每个节点的值v以及激活值a
(3)计算最后一层节点的“残差”。对于神经网络的最后一层输出层,因为可以直接算出网络产生的激活值与实际值之间的差距,所以很容易计算损失函数对最后一层的偏导数。假设第K层为输出层,则:
即输出层的第 i 个节点的残差为:(该点的激活值-该点的真实值)*该点激活函数对该点值得导数
(4)对于第K-1层的残差,可以根第K层的残差计算出来:
简而言之:
(多打了一个“=”)
也就是说,前一层某个神经元的残差 是由后一层中每个神经元贡献的,其贡献的份额是由二者之间的连接权决定的,并且作用上前一层激活函数的导数。
(5)逐层计算每个节点的残差值,根据(4)中的结果,用 K-2 代替 K-1,用 K-1 代替 K 则得到 K-2 层的残差。以此类推可以得到前面各层的连接权和偏置值得残差。
(6)根据连接权和偏置值的梯度下降法迭代公式即可得到其新的迭代值。
(7)当我们输入一个训练样本室,就可以根据(2)-(6),对W和b进行更新。