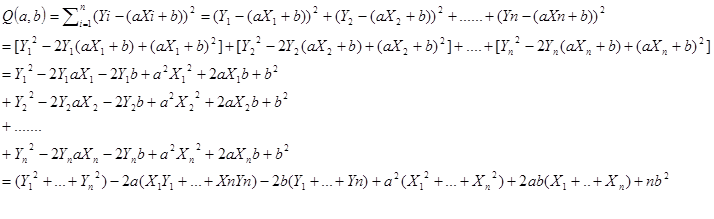回归分析的目的

回归分析的目的大致可分为两种：
第一，预测。预测目标变量，求解目标变量y和说明变量(x1，x2，…)的方程。
$y=a_0+b_1{x}_1+b_2{x}_2+\dots +b_k{x}_k+误差$

把上述方程叫做(多元)回归方程或者(多元)回归模型。a0是y截距，b1，b2，…，bk是回归系数。当k=1时，只有1个说明变量，叫做一元回归方程。根据最小平方法求解最小误差平方和，非求出y截距和回归系数。若求解回归方程．分別代入x1，x2，…xk的数值，预测y的值。

第二，因子分析。因子分析是根据回归分析结果，得出各个自变量对目标变量产生的影响，因此，需要求出各个自变量的影响程度。

这里介绍一下，最小平方法：
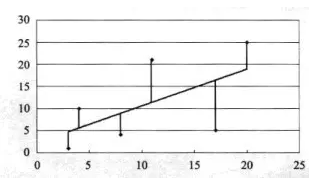
分别从散点图的各个数据标记点，做一条平行于y轴的平行线，相交于图中直线(如下图)

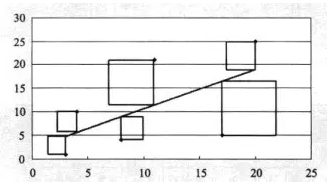
平行线的长度在统计学中叫做“误差”或者‘残差”。误差(残差)是指分析结果的运算值和实际值之间的差。接这，求平行线长度曲平方值。可以把平方值看做边长等于平行线长度的正方形面积(如下图)

最后，求解所有正方形面积之和。确定使面积之和最小的a(截距)和b(回归系数)的值(如下图)。

线性回归步骤

线性回归的步骤不论是一元还是多元相同，步骤如下：
1、散点图判断变量关系（简单线性）；
2、求相关系数及线性验证；
3、求回归系数，建立回归方程；
4、回归方程检验；
5、参数的区间估计；
6、预测；

一元线性回归操作和解释

在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。举个例子来说吧：
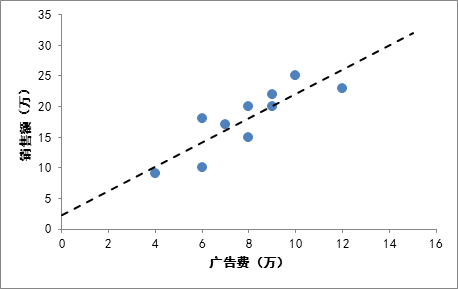
比方说有一个公司，每月的广告费用和销售额，如下表所示：

如果我们把广告费和销售额画在二维坐标内，就能够得到一个散点图，如果想探索广告费和销售额的关系，就可以利用一元线性回归做出一条拟合直线：

• 这条线是怎么画出来的？

对于一元线性回归来说，可以看成Y的值是随着X的值变化，每一个实际的X都会有一个实际的Y值，我们叫Y实际，那么我们就是要求出一条直线，每一个实际的X都会有一个直线预测的Y值，我们叫做Y预测，回归线使得每个Y的实际值与预测值之差的平方和最小，即$（Y1实际-Y1预测{）}^2+（Y2实际-Y2预测{）}^2+\dots \dots +（Yn实际-Yn预测{）}^2$的和最小
用数学符号来表示就是：
$Q(a,b)={\sum }_{i-1}^n(Y_i-(a{X}_i+b))$
只需要求出让Q最小的a和b的值，那么回归线的也就求出来了。那么，要求a，b的值，就是求a，b等于多少的时候，这个函数Q最小。对于函数Q，分别对于a和b求偏导数，然后令偏导数等于0，就可以得到一个关于a和b的二元方程组，就可以求出a和b了。这个方法被称为最小二乘法。
该函数展开式为：

然后利用平均数，把上面式子中每个括号里的内容进一步化简。例如下面的公式：
$(Y_1^2+...Y_n^2)/n=\overline{Y^2}$

所以原式可以化为：
$Q(a,b)=n\overline{Y^2}-2an\overline{XY}-2b\overline{Y}+a^{2}n\overline{X^2}+2abn\overline{X}+n{b}^2$

然后对于展开式，分别对a和b求偏导，并令其为0。
$\frac{\partial Q}{\partial a}=-2n\overline{XY}+2an\overline{X^2}+2bn\overline{X}=0$

$\frac{\partial Q}{\partial b}=-2n\overline{Y}+2ab\overline{X}+2nb=0$

进一步化简，可以消掉2n。
最后得出a、b的求解公式为：

$a=\frac{\overline{X}\cdot \overline{Y}-\overline{XY}}{(\overline{X}{)}^2-\overline{X^2}}$

$b=\overline{Y}-a\overline{X}$

而$\overline{X}$和$\overline{Y}$和$\overline{XY}$很容易根据已知数据求出来。
有了这个公式，对于上述广告费和销售额的栗子，我们可以算出$a=1.98$，$b=2.25$，最终回归拟合的直线为$Y=1.98X+2.25$。所以，根据这个直线很容易作出预测，当投入广告为2万的时候，预计销售额为6.2万。

评价回归线拟合程度的好坏

我们画出的拟合直线只是一个近似，因为肯定很多的点都没有落在直线上，那么我们的直线拟合程度到底怎么样呢？在统计学中有一个术语叫做$R^2$（coefficient ofdetermination，中文叫判定系数、拟合优度），用来判断回归方程的拟合程度。
首先要明确一下如下几个概念：
总偏差平方和（又称总平方和，SST，Sum of Squaresfor Total）：是每个因变量的实际值（给定点的所有Y）与因变量平均值（给定点的所有Y的平均）的差的平方和，即，反映了因变量取值的总体波动情况。如下：
$SST={\sum }_{i-1}^n(Y_i-\overline{Y}{)}^2$
回归平方和（SSR，Sum of Squares forRegression）：因变量的回归值（直线上的Y值）与其均值（给定点的Y值平均）的差的平方和，即，它是由于自变量x的变化引起的y的变化，反映了y的总偏差中由于x与y之间的线性关系引起的y的变化部分，是可以由回归直线来解释的。
$SSR={\sum }_{i-1}^n(\widetilde{Y_i}-\overline{Y}{)}^2$

残差平方和（又称误差平方和，SSE，Sum of Squaresfor Error）:因变量的各实际观测值(给定点的Y值)与回归值（回归直线上的Y值）的差的平方和，它是除了x对y的线性影响之外的其他因素对y变化的作用，是不能由回归直线来解释的。

就拿广告费和销售额的例子来说，其实广告费只是影响销售额的其中一个比较重要的因素，可能还有经济水平、产品质量、客户服务水平等众多难以说清的因素在影响最终的销售额，那么实际的销售额就是众多因素相互作用最终的结果，由于销售额是波动的，所以用上文提到的每个月的销售额与平均销售额的差的平方和（即总平方和）来表示整体的波动情况。
也就是说：
$SST（总偏差）=SSR（回归线可以解释的偏差）+SSE（回归线不能解释的偏差）$

拟合程度的判断就由如下的公式得到：
$R^2=SSR/SST$
$R^2$的取值在0，1之间，越接近1说明拟合程度越好
假如所有的点都在回归线上，说明SSE为0，则$R^2=1$，意味着Y的变化100%由X的变化引起，没有其他因素会影响Y，回归线能够完全解释Y的变化。如果$R^2$很低，说明X和Y之间可能不存在线性关系
还是回到最开始的广告费和销售额的例子，这个回归线的$R^2$为0.73，说明拟合程度还凑合。

变量的显著性检验

变量的显著性检验的目的：剔除回归系数中不显著的解释变量（也就是X），使得模型更简洁。在一元线性模型中，我们只有有一个自变量X，就是要判断X对Y是否有显著性的影响；多元线性回归中，验证每个Xi自身是否真的对Y有显著的影响，不显著的就应该从模型去掉。

检测的方式将在以后的文章中提到。

对于所有的回归模型的软件，最终给出的结果都会有参数的显著性检验，忽略掉难懂的数学，我们只需要理解如下几个结论：

• T检验用于对某一个自变量Xi对于Y的线性显著性，如果某一个Xi不显著，意味着可以从模型中剔除这个变量，使得模型更简洁。
• F检验用于对所有的自变量X在整体上看对于Y的线性显著性
• T检验的结果看P-value，F检验看Significant F值，一般要小于0.05，越小越显著（这个0.05其实是显著性水平，是人为设定的，如果比较严格，可以定成0.01，但是也会带来其他一些问题，不细说了）
• 一般来说，只要F检验和关键变量的T检验通过了，模型的预测能力就是OK的。