scipy中线性规划的标准表达形式

现在来解决一个实际的问题

python代码

用scipy求解

# -*- coding: utf-8 -*-
"""
Created on Sun Sep 26 10:21:41 2021
@author: songyuhui
function： 利用scipy实现最优化问题
        eg：目标函数：max z = 2x1 + 3x2- 5x3
            约束条件： x1 + x2+ x3 = 7
                     2x1 - 5x2 + x3 >= 10
                     x1 + 3x2 + x3 <= 12
                     x1,x2,x3 >=0
        用optimize库在求解时全部都要转化成标准形式：
        目标函数：min c^T x 
        约束条件： Ax <= B
                  Aeq*x =Beq
                  LB<= x <=UB
        求解代码为：
        求解函数：res=optimize.linprog(C,A,B,Aeq,Beq,LB,UB,Xo,options)
        结果：         res
        目标函数最小值：res.fun 
        最优解         res.x
        
"""

#用scipy解上面的例题，用optimize解标准形式是最小值，要通过添加负号变为标准式
#导入包
from scipy import optimize
import numpy as np

#确定C,A,B,Aeq,beq
C=np.asarray([2,3,-5]) #目标函数系数
A=np.asarray([[-2,5,-1],[1,3,1]])#不等式左边系数，注意>=的式子要转化为<=的式子，故前面2,-5,1要加负号，
B=np.asarray([-10,12]) #不等式右边的数
Aeq=np.asarray([[1,1,1]])#等式左边系数，这里是两个方括号，因为要写为一维行矩阵，列表默认的是按列排
Beq=np.asarray([7])# 等式右边的数

#求解
res=optimize.linprog(-C,A,B,Aeq,Beq)#调用optimize类里面的linprog方法计算最小值，算最大值要写-c，返回结果给res
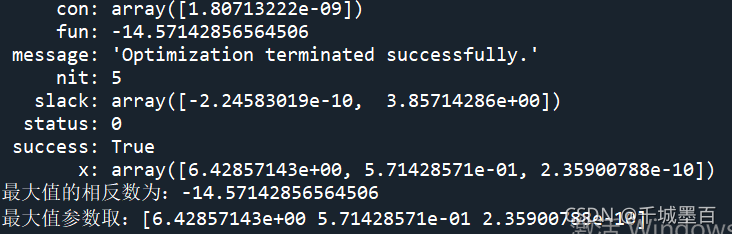
print(res)
print('最大值的相反数为：{}'.format(res.fun))
print('最大值参数取：{}'.format(res.x))

结果展示

用pulp包求解

############用pulp求解#############
import pulp
#目标函数系数
z=[2,3,-5]
#约束
a=[[2,-5,1],[-1,-3,-1]] #不等式约束的系数，全部写成>=,或者全部写成<=，注意符号
b=[10,-12]
aeq=[[1,1,1]]
beq=[7]
#确定最大化最小化，最大化用LPMaximize 最小化用LPMinimize
m=pulp.LpProblem(sense=pulp.LpMaximize)

#定义三个变量放到变量列表中
x=[pulp.LpVariable(f'x{i}',lowBound=0)for i in [1,2,3]]
#定义目标函数，lpDot可以将两个列表的对应位相乘再加
m+= pulp.lpDot(z,x)#结果为z[1]*x[1]+z[2]*x[2]+z[3]*x[3]

#设置不等式约束
for i in range(len(a)):
    m+=(pulp.lpDot(a[i],x)>=b[i])

#设置等式约束
for i in range(len(aeq)):
    m+=(pulp.lpDot(aeq[i],x)==beq[i])
#求解
m.solve()
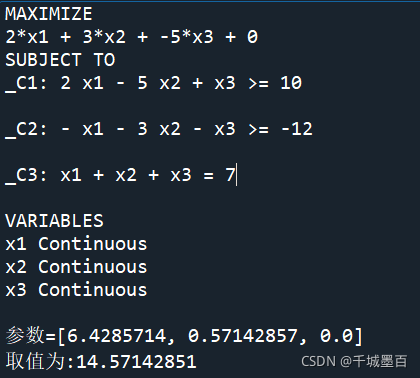
print(m)
print("参数={}".format([pulp.value(var)for var in x]))
print(f'取值为:{pulp.value(m.objective)}')

结果展示