往期
- 【用deepseek和chatgpt做算法竞赛】——华为算法精英实战营第十九期-Minimum Cost Trees_0:介绍了题目和背景
- 【用deepseek和chatgpt做算法竞赛】——华为算法精英实战营第十九期-Minimum Cost Trees_1:题目输入的格式说明,选择了邻接表来表示图
0 邻接表是如何表示图的
邻接表是一种常用的图的存储结构,主要用于存储稀疏图(即边较少的图)。它的核心思想是用一个数组 + 链表的结构来存储图中的顶点和它们的邻接关系。
0.1 邻接表的结构
- 顶点数组(Vertex Array): 存储所有顶点,每个顶点指向一个链表。
- 邻接链表(Adjacency List):存储与该顶点直接相连的所有顶点(即邻居)。
0.2 邻接表的示例
无向图:
A
/ \
B - C
邻接表: (ABC都是互通的,所有每个顶点都可以抵达其他两点)
A → B → C
B → A → C
C → A → B
有向图:
A → B
A → C
B → C
邻接表:(A可以通向BC,但BC则不可以)
A → B → C
B → C
C → ∅
0.3 邻接表的特点
✅ 节省空间:对于稀疏图,邻接表比邻接矩阵节省空间,因为它只存储实际存在的边。
✅ 遍历某个顶点的邻居速度快:访问某个顶点的所有相邻顶点时,时间复杂度是 O(度数)。
✅ 适用于存储无向图、有向图和带权图:可以额外在链表中存储权重信息。
⚠ 不适合查找是否有某条边:判断两个顶点是否直接相连的时间复杂度是 O(度数),比邻接矩阵的 O(1) 要慢。
0.4 邻接表的应用
😊社交网络(每个人的朋友关系) 😊网络路由(存储节点的连通信息)
😊游戏地图(存储不同地点之间的通路) 😊搜索引擎的网页链接关系
1 输出格式介绍
- 在第一行,打印一个整数 f,表示找到的有向树的数量(1 ≤ f ≤ 2)。
- 接下来,打印 f 棵有向树。每棵树需要按照以下格式描述:
在每棵树的第一行,打印一个整数 w,表示该树中的有向边数量。
在接下来的 w 行中,按照以下格式输出树的边:
第 (i + 1) 行打印两个整数 (aᵢ, bᵢ),表示一条有向边的起点 aᵢ 和终点 bᵢ。
该边 (aᵢ, bᵢ) 必须存在于输入图中,并且只能被打印一次。
所有打印的边必须构成一个有效的有向树,该树以 s 为根,能够到达所有 tᵢ。
1.1 例子解释
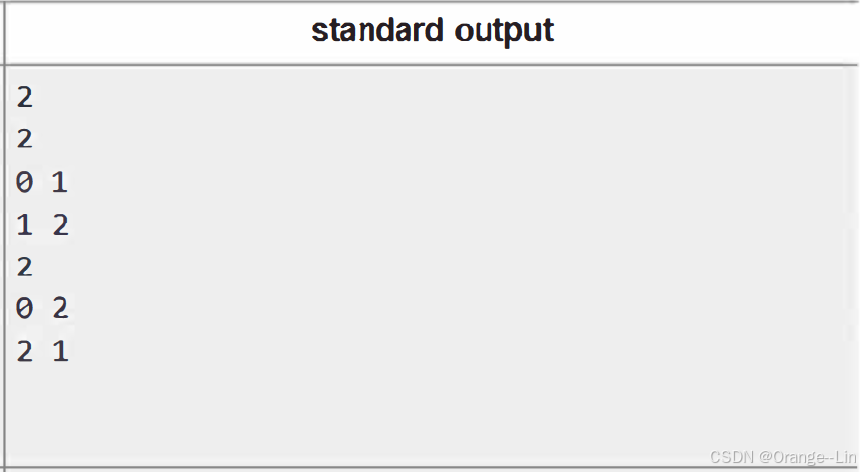
下图是规则里的一个标准输出
我们逐行解析它的含义
- 第一行”2“:这个数字 2 表示找到了 2 棵有向树。
- 第一棵树
2
0 1
1 2
2 表示该树有 2 条有向边。
0 1 表示存在一条 从 0 到 1 的有向边。
1 2 表示存在一条 从 1 到 2 的有向边。
0
↓
1
↓
2
这棵树满足有向树的定义:无环、无多余边、从根可达所有节点。
- 第二棵树
2
0 2
2 1
0
↓
2
↓
1
这份标准输出描述了 两个不同的有向树,它们都是从 0 作为根节点,连接了图中的所有节点:
第一棵树的结构:0 → 1 → 2
第二棵树的结构:0 → 2 → 1