诸神缄默不语-个人CSDN博文目录
cs224w（图机器学习）2021冬季课程学习笔记集合

colab 3 文件原始下载地址

我将写完的colab 3文件发到了GitHub上，有一些个人做笔记的内容。地址：cs224w-2021-winter-colab/CS224W_Colab_3.ipynb at master · PolarisRisingWar/cs224w-2021-winter-colab

本colab主要实现：
实现GraphSAGE和GAT模型，应用在Cora数据集上。
使用DeepSNAP包切分图数据集、实现数据集转换，完成边属性预测（链接预测）任务。

1. 实现GraphSAGE和GAT

在colab 2¹ 中，我们是直接使用PyG内置的GCNConv来建模。在本colab中，我们将自己设计message-passing模型，建立单层GNN，并实现一个可泛化的堆叠GNN模型，应用在CORA数据集上。
CORA数据集是一张引用网络，节点是文档，无向边是引用关系。每个节点有所隶属类标签。节点特征是文档 词包BoW 表示的元素。数据集中共2708个节点，5429条边（注意PyG中无向边的edge_index的第二维是2倍边数），7类标签，每个节点有1433维特征。
在本colab中，CORA数据集通过PyG的Planetoid加载。
对PyG数据集的介绍可参考我之前写的博文：PyTorch Geometric (PyG) 入门教程
针对Planetoid有时可能无法直接下载数据的问题，可参考我写的博文：Planetoid无法直接下载Cora等数据集的3个解决方式

呃……顺带再提一嘴，这里的实现逻辑都是transductive的，至于怎么搞inductive的我还不知道。
我已经很累了，我的脑子不支持这么复杂的东西。

1.1 可泛化的GNN堆叠模型

GNN模型，可以直接应用自己写的GraphSAGE、GAT等单层模型。
由 message-passing + post-message-passing（即 Lecture 7² 中讲的post-process layers）2部分组成。
注意，在代码中 x = F.dropout(x, p=self.dropout,training=self.training) 这一句，在原代码中是没有加 self.training 的。我用我的代码常识认为是老师写错了³。而且我发现增加 self.training 后结果确实有了提升⁴，所以我觉得确实大概是老师写错了。

import torch
import torch_scatter
import torch.nn as nn
import torch.nn.functional as F

import torch_geometric.nn as pyg_nn
import torch_geometric.utils as pyg_utils

from torch import Tensor
from typing import Union, Tuple, Optional
from torch_geometric.typing import (OptPairTensor, Adj, Size, NoneType,
                                    OptTensor)

from torch.nn import Parameter, Linear
from torch_sparse import SparseTensor, set_diag
from torch_geometric.nn.conv import MessagePassing
from torch_geometric.utils import remove_self_loops, add_self_loops, softmax

class GNNStack(torch.nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, args, emb=False):
    	#emb参数如果置False，将返回分类结果（经softmax后的结果）；反之直接输出最后一层的表示向量
    	#跟 colab 2 的return_embeds参数差不多
        super(GNNStack, self).__init__()

		#message-passing部分
        conv_model = self.build_conv_model(args.model_type)  #单层GNN（GraphSAGE或GAT）
        self.convs = nn.ModuleList()
        self.convs.append(conv_model(input_dim, hidden_dim))
        assert (args.num_layers >= 1), 'Number of layers is not >=1'
        #如果args.num_layers不河狸（<1）时报错
        for l in range(args.num_layers-1):
            self.convs.append(conv_model(args.heads * hidden_dim, hidden_dim))  
            #args.heads在GAT模型中是设置attention头数的参数

        #post-message-passing部分
        self.post_mp = nn.Sequential(
            nn.Linear(args.heads * hidden_dim, hidden_dim),  #GAT输出的特征维度就是args.heads*hidden_dim
            nn.Dropout(args.dropout),   #args.dropout参数是dropout的概率
            nn.Linear(hidden_dim, output_dim))

        self.dropout = args.dropout
        self.num_layers = args.num_layers

        self.emb = emb

    def build_conv_model(self, model_type):
        if model_type == 'GraphSage':
            return GraphSage
        elif model_type == 'GAT':
            return GAT

    def forward(self, data):
        x, edge_index, batch = data.x, data.edge_index, data.batch
          
        for i in range(self.num_layers):
        	#单层卷积网络
            x = self.convs[i](x, edge_index)
            x = F.relu(x)
            #x = F.dropout(x, p=self.dropout) 这个是原代码
            x = F.dropout(x, p=self.dropout,training=self.training)

		#post-message-passing
        x = self.post_mp(x)

        if self.emb == True:
            return x

        return F.log_softmax(x, dim=1)
        #总之是softmax→取对数，具体细节还没看

    def loss(self, pred, label):
        return F.nll_loss(pred, label)
        #总之是适用于训练分类问题的损失函数，具体细节还没看

1.2 单层GNN在PyG中的实现

PyG官方文档：Creating Message Passing Networks — pytorch_geometric 1.7.2 documentation

（虽然官方文档中讲了边和EdgeConv的事，但是课程中没讲，所以我在这里也只提一下，我就不去研究了）

图卷积神经网络可泛化为信息传递或邻居聚合模型，即如下公式：
$${\mathbf{x}}_i^{(k)}={\gamma }^{(k)}\left({\mathbf{x}}_i^{(k-1)},{\square }_{j\in \mathcal{N}(i)}{\varphi }^{(k)}({\mathbf{x}}_i^{(k-1)},{\mathbf{x}}_j^{(k-1)},{\mathbf{e}}_{j,i})\right)$$
下标是节点索引，上标是网络层数。
${\mathbf{x}}_i^{(k)}\in {\mathbb{R}}^F$ 是节点 $i$ 在第 $k$ 层的节点特征（即该节点的表示向量）。
${\mathbf{e}}_{j,i}\in {\mathbb{R}}^D$（可选）是 $j\to i$ 这条边的特征。
$\square$ 是一个可微分的、且 permutation invariant⁵ 的函数，用于聚合邻居信息，如sum、mean、max等。
$\gamma$ 和 $\varphi$ 都是可微分的函数，如MLP等。
（这个公式有点跟课上讲的不太一样，一是这里带上了边特征，二是在信息转换和聚合邻居的时候也把自己带上了（当然我理解就是说，以 $\varphi$ 为例，里面有 ${\mathbf{x}}_i$、${\mathbf{x}}_j$、${\mathbf{e}}_{j,i}$，但是可以不全用，比如本colab中就只对 ${\mathbf{x}}_j$ 做信息转换）。但是也可以说差不多，都是message+aggregation，事都是这么一回事儿）

1.2.1 MessagePassing 基类

MessagePassing官方文档

就用这个的话，就可以自动做聚合（即公式中的 $\square$ ）工作，用户只需要考虑 $\varphi$（如使用 message() 方法）和 $\gamma$（如使用 update() 方法）。
聚合scheme可选：aggr="add", aggr="mean" or aggr="max"
（但是在本colab中的选择是手动写了 aggregate() 函数。呃……其实我猜噢，大概是因为以前版本的MessagePassing没有这个功能。我觉得应该用处一样，以后有时间或许可以试验一下）

大致运行逻辑是：

1. 在 forward() 函数中运行主要功能（跟普通Module一样），并调用 propagate() 函数。
   普适范式：pre-processing → propagate → post-processing

2. propagate() 函数内置自动调用 message()、aggregate() 和 update() 函数。就有什么要用的参数（如 x）直接传到 propagate() 函数中即可。

1.2.1.2 定义类

MessagePassing(aggr="add", flow="source_to_target", node_dim=-2)
aggr参数：选择聚合scheme。
flow参数：message passing的flow direction，“source_to_target” or “target_to_source”。区别见下述 message 方法。
node_dim参数：聚合维度。这个默认的-2就是节点数量的那个维度（x的尺寸是 [|V|,d] 嘛），就是对邻居节点进行聚合的这个维度嘛。

1.2.1.3 propagate() 方法

MessagePassing.propagate(edge_index, size=None, **kwargs)
传播信息。
不止允许对称邻接矩阵⁶（尺寸为 [N, N] ）的情况（size为None时的默认情况），也接受 general sparse assignment matrices（如 bipartite graph）的情况，如尺寸为 [N, M]，需要传入参数 size=(N, M)。
对于有两组节点和索引、且分别拥有自己信息的bipartite graph，这种切分可通过传入tuple格式信息来进行标记：x=(x_N, x_M)（对这一点的理解可见GraphSAGE部分的代码注释）

1.2.1.4 message() 方法

MessagePassing.message(...)
信息转换，类似于公式中的 $\varphi$。
具体来说，是用于构建传播至节点 $i$ 的信息，如果 flow="source_to_target" 就指考虑所有 $(j,i)\in ϵ$ 的边（就是，一般来说都是这样的嘛），如果 flow="target_to_source" 就考虑所有 $(i,j)\in ϵ$ 的边。
能使用所有传入 propagate() 的参数。
此外，对传入 propagate() 的Tensor（如 x），可以通过在变量名后分别加 _i 和 _j 来将其映射到不同的节点组上（如 x_i 和 x_j）。一般 $i$ 指聚合信息的中心节点，$j$ 指邻居节点，如公式所用。（每个Tensor都能这么分，只要有source或destination的节点特征）

1.2.1.5 update() 方法

MessagePassing.update(aggr_out, ...)
对所有节点更新节点嵌入，类似于公式中的 $\gamma$。
以聚合过程的输出作为第一个入参，也能使用所有传入 propagate() 的参数。

1.2.2 官方文档示例：Implementing the GCN Layer

GCN公式：
x i ( k ) = ∑ j ∈ N ( i ) ∪ { i } 1 deg ⁡ ( i ) ⋅ deg ⁡ ( j ) ⋅ ( Θ ⋅ x j ( k − 1 ) ) \mathbf{x}_i^{(k)} = \sum_{j \in \mathcal{N}(i) \cup \{ i \}} \frac{1}{\sqrt{\deg(i)} \cdot \sqrt{\deg(j)}} \cdot \left( \mathbf{\Theta} \cdot \mathbf{x}_j^{(k-1)} \right) xi(k)​=j∈N(i)∪{i}∑​deg(i) ​⋅deg(j) ​1​⋅(Θ⋅xj(k−1)​)
message passing：权重矩阵 $\mathbf{\Theta }$ → 归一化（度数）→ 聚合邻居信息
（这个归一化方式和课程中² 讲的也不太一样，课程中归一化使用的是中心节点的度数）

这个公式可以被拆分成如下步骤：

1. 在邻接矩阵中增加自环（说起来课程中也没有自环这回事……到底加不加自环？是各种论文/实现方式本来就是画风不一样吗还是因为啥啊？）
2. 对节点特征矩阵进行线性转换（$\mathbf{\Theta }$）
3. 计算归一化系数
4. 归一化节点特征（$\varphi$）
5. 加总邻居节点特征（"add" aggregation）

前三步一般在message passing前进行（也就是在forward中直接调用），4-5步可在MessagePassing基类中处理。

创建 message passing 层的代码：

import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree

class GCNConv(MessagePassing):
    def __init__(self, in_channels, out_channels):
        super(GCNConv, self).__init__(aggr='add')  # "Add" aggregation (Step 5).
        self.lin = torch.nn.Linear(in_channels, out_channels)

    def forward(self, x, edge_index):
        # x has shape [N, in_channels]
        # edge_index has shape [2, E]

        # Step 1: Add self-loops to the adjacency matrix.
        edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))

        # Step 2: Linearly transform node feature matrix.
        x = self.lin(x)

        # Step 3: Compute normalization.
        row, col = edge_index  #这个row和col是COO格式储存邻接矩阵的edge_index的坐标
        #也就是每个边的起点和终点
        deg = degree(col, x.size(0), dtype=x.dtype)  #得到各节点的度数
        deg_inv_sqrt = deg.pow(-0.5)
        deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0  #这句话有点没搞懂，会出现这种情况吗？
        norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]  #尺寸为[num_edges, ]

        # Step 4-5: Start propagating messages.
        return self.propagate(edge_index, x=x, norm=norm)

    def message(self, x_j, norm):
        # x_j has shape [E, out_channels]
        #x_j包含了每个边的source node的特征（节点邻居特征）

        # Step 4: Normalize node features.
        return norm.view(-1, 1) * x_j
        #https://pytorch.org/docs/stable/generated/torch.mul.html
        #把norm拉成[E,1]尺寸,这两个矩阵就broadcastable了，就可以进行乘法运算了
        #对每个边，norm与x_j逐元素相乘。结果的尺寸是[E,out_channels]        

在文档中说 message() 里的 x_j 是一个lifted tensor……这又是什么玩意啊？

直接调用 message passing 网络层的代码：

conv = GCNConv(16, 32)
x = conv(x, edge_index)

1.2.3 在本colab中的应用

不显示调用 update()，而在 forward() 中实现其功能。

1.2.3.1 GraphSAGE

PyG对GraphSAGE的官方实现内置函数SAGEConv文档

在本colab中，对GraphSAGE增加了skip connections²。

GraphSAGE公式：
h v ( l ) = W l ⋅ h v ( l − 1 ) + W r ⋅ AGG ( { h u ( l − 1 ) , ∀ u ∈ N ( v ) } ) h_v^{(l)} = W_l\cdot h_v^{(l-1)} + W_r \cdot\text{AGG}\left(\{h_u^{(l-1)}, \forall u \in N(v) \}\right) hv(l)​=Wl​⋅hv(l−1)​+Wr​⋅AGG({hu(l−1)​,∀u∈N(v)})
简化的AGG函数：
AGG ( { h u ( l − 1 ) , ∀ u ∈ N ( v ) } ) = 1 ∣ N ( v ) ∣ ∑ u ∈ N ( v ) h u ( l − 1 ) \text{AGG}\left(\{h_u^{(l-1)}, \forall u \in N(v) \}\right) = \frac{1}{|N(v)|} \sum_{u\in N(v)} h_u^{(l-1)} AGG({hu(l−1)​,∀u∈N(v)})=∣N(v)∣1​u∈N(v)∑​hu(l−1)​
在每次迭代后增加了L2正则化。

代码：

class GraphSage(MessagePassing):
    
    def __init__(self, in_channels, out_channels, normalize = True,
                 bias = False, **kwargs):
        #bias这个参数没用的样子
        super(GraphSage, self).__init__(**kwargs)

        self.in_channels = in_channels
        self.out_channels = out_channels
        self.normalize = normalize

        self.lin_l=Linear(in_channels,out_channels)  #W_l，对中心节点应用
        self.lin_r=Linear(in_channels,out_channels)  #W_r，对邻居节点应用

        self.reset_parameters()

    def reset_parameters(self):
        self.lin_l.reset_parameters()
        self.lin_r.reset_parameters()

    def forward(self, x, edge_index, size = None):
        # message-passing + post-processing
        out=self.propagate(edge_index,x=(x,x),size=size)  #message passing
        #(x,x)见后文讲解
        x=self.lin_l(x)  #自环
        out=self.lin_r(out)  #邻居信息
        out=out+x
        if self.normalize:  #L2
            out=F.normalize(out)
		
		return out

    def message(self, x_j):
		out=x_j
		return out

    def aggregate(self, inputs, index, dim_size = None):
        # The axis along which to index number of nodes.
        node_dim = self.node_dim
        
		out=torch_scatter.scatter(inputs,index,node_dim,dim_size=dim_size,reduce='mean')
		#这个函数我也还没看懂，以后再研究吧
		
		return out

本colab中类的 reset_parameters() 方法好像跟colab 2里的一样都没什么用的样子。

关于 out=self.propagate(edge_index,x=(x,x),size=size) 中的入参 x：
这个在原代码中要求传入(x,x)，但是我只传了x试了一下（参考GCN那个示例），也能跑，而且对应结果的最大accuracy跑了两次分别是0.8和0.782，参考⁴的结果，总之就跟(x,x)的结果差不多。
我对此的理解就是：两种写法都可以。colab中说是因为对中心节点和邻居节点的表示是相同的，但我没搞懂这是指啥。
但是确实在PyG自己对GraphSAGE的实现（SAGEConv）代码中也是用的(x,x)：

图片截自：torch_geometric.nn.conv.sage_conv — pytorch_geometric 1.7.2 documentation

就我思索了一下，这种级别的问题非看源码或问作者不可解决了，但我没看懂MessagePassing的源代码，所以算了。我就说明一下这个情况：直接用x的典例当属在本笔记中也写过的GCN的代码，用(x,x)的典例就是这块了。

顺带一提，那个 message() 的源代码里本来就是返回 x_j 的：

图片来源：torch_geometric.nn.conv.message_passing — pytorch_geometric 1.7.2 documentation

所以我觉得其实应该不用专门再重写一遍 message()？但是还是跟上面的(x,x)一样，就是SAGEConv的官方实现里面确实也是这么写的就是了……

1.2.3.2 GAT

PyG对GAT的官方实现内置函数GATConv文档

单层GAT实现逻辑：

1. 对每个节点应用线性转换（一个共享参数 $\mathbf{W}\in {\mathbb{R}}^{F^{\prime }\times F}$，其中 $F$ 是输入特征维度，$F^{\prime }$ 是输出特征维度）

2. 在所有节点上应用一个共享的注意力机制 $a$（在本colab中是对两个节点分别应用一个单层前馈神经网络，输出都是标量；然后加总这一标量；经 LeakyReLU（negative input slope 0.2） 这一激活函数，得到最后输出）：${\mathbb{R}}^{F^{\prime }}\times {\mathbb{R}}^{F^{\prime }}\to \mathbb{R}$

3. 通过注意力机制 $a$ 计算得到attention coefficient $e_{ij}=a({\mathbf{W}}_{\mathbf{l}}\overrightarrow{h_i},{\mathbf{W}}_{\mathbf{r}}\overrightarrow{h_j})$，$e_{ij}$ 捕捉到的是节点 $j$ 对节点 $i$ 的重要性。
   （注意虽然这两个权重矩阵写起来不一样，但是根据课程² 和原论文（Veličković P, Cucurull G, Casanova A, et al. Graph attention networks[J]. arXiv preprint arXiv:1710.10903, 2017. ），这两个矩阵可以是同一个矩阵，而且最后的实现以及GAT官方实现中确实也都是同一个矩阵⁷……所以我觉得下标是扯淡来的）
   （跟学长讨论了一下，这里共享参数应该是考虑到GAT参数太多，所以这么干的）
   （对于这两个权重是不是确实应该是同一个权重，我也做了下实验，即更换代码中的 self.lin_r = self.lin_l 此句和 self.lin_r=Linear(in_channels,heads*out_channels)，分别计算其对应的GAT计算出的最大accuracy和训练用时。
   实验结果是用时和最大accuracy的结果差不多。
   呃，可能数据量大的话会体现出代价上的差距？）

4. 在普适的self-attention模型中，每个节点是计算对其他全部节点的重要性的，这也就没有了图结构信息。为了应用图结构信息，可以用masked attention，即只计算某节点邻居对其重要性。⁸

5. 为便于比较不同节点间的attention coefficient，在所有邻居节点上通过softmax对其正则化：${\alpha }_{ij}={\text{softmax}}_j(e_{ij})=\frac{\exp (e_{ij})}{{\sum }_{k\in {\mathcal{N}}_i}\exp (e_{ik})}$

6. 设注意力机制的权重参数为 $\overrightarrow{a}\in {\mathbb{R}}^{F^{\prime }}$，则最终权重的计算公式可以写成：
   ${\alpha }_{ij}=\frac{\exp \left(\text{LeakyReLU}\right({\overrightarrow{a_l}}^T{\mathbf{W}}_{\mathbf{l}}\overrightarrow{h_i}+{\overrightarrow{a_r}}^T{\mathbf{W}}_{\mathbf{r}}\overrightarrow{h_j}\left)\right)}{{\sum }_{k\in {\mathcal{N}}_i}\exp \left(\text{LeakyReLU}\right({\overrightarrow{a_l}}^T{\mathbf{W}}_{\mathbf{l}}\overrightarrow{h_i}+{\overrightarrow{a_r}}^T{\mathbf{W}}_{\mathbf{r}}\overrightarrow{h_k}\left)\right)}$
   在代码中用 ${\alpha }_i$ 表示 ${\overrightarrow{a_l}}^T{\mathbf{W}}_{\mathbf{l}}\overrightarrow{h_i}$，${\alpha }_j$ 表示 ${\overrightarrow{a_r}}^T{\mathbf{W}}_{\mathbf{r}}\overrightarrow{h_j}$

7. 通过权重计算聚合值：$h_i^{\prime }={\sum }_{j\in {\mathcal{N}}_i}{\alpha }_{ij}{\mathbf{W}}_{\mathbf{r}}\overrightarrow{h_j}$

8. 应用多头机制：${\overrightarrow{h_i}}^{\prime }=|{|}_{k=1}^K({\sum }_{j\in {\mathcal{N}}_i}{\alpha }_{ij}^{(k)}{{\mathbf{W}}_{\mathbf{r}}}^{(k)}\overrightarrow{h_j})$（${\mathbf{h}}^{\prime }\in {\mathbb{R}}^{K{F}^{\prime }}$）
   上标 $k$ 指对应的头

以下代码有部分内容经评论区读者提醒修正。但是GitHub项目里的colab没有改，因为我懒

代码：

class GAT(MessagePassing):

    def __init__(self, in_channels, out_channels, heads = 2,
                 negative_slope = 0.2, dropout = 0., **kwargs):
        super(GAT, self).__init__(node_dim=0, **kwargs)

        self.in_channels = in_channels
        self.out_channels = out_channels
        self.heads = heads
        self.negative_slope = negative_slope
        self.dropout = dropout

        self.lin_l=Linear(in_channels,heads*out_channels)  #W_l
        #根据GNNStack()，这里的in_channels除第一层外就都是已经乘过heads的数字
        
        self.lin_r = self.lin_l  #W_r

        self.att_l = Parameter(torch.Tensor(1, heads, out_channels))  #\overrightarrow{a_l}
        self.att_r = Parameter(torch.Tensor(1, heads, out_channels))  #\overrightarrow{a_r}
        #我抄的代码就是用的Parameter，我看了一下PyG的GATConv源码也用的是Parameter
        #至于为什么不用Linear可能是因为Linear不方便这么处理三维张量？

        self.reset_parameters()

    def reset_parameters(self):
        nn.init.xavier_uniform_(self.lin_l.weight)
        nn.init.xavier_uniform_(self.lin_r.weight)
        nn.init.xavier_uniform_(self.att_l)
        nn.init.xavier_uniform_(self.att_r)

    def forward(self, x, edge_index, size = None):
        H, C = self.heads, self.out_channels

        #线性转换
        x_l=self.lin_l(x)  #W_l*h_i [N,H*C]
        #x就是h的转置        
        x_r=self.lin_r(x)  #W_r*h_j
        
        x_l=x_l.view(-1,H,C)  #[N,H,C]
        x_r=x_r.view(-1,H,C)
        alpha_l = (x_l * self.att_l).sum(axis=-1)
        #\overrightarrow{a_r}^T * Wl * hi
        #沿C汇总。这部分是经评论区读者发现，然后我看了一下PyG自己的GATConv是这么实现的
        #我想了一下确实应该是沿特征汇总才对，因为矩阵运算就是加起来嘛……
        #代码中点乘部分就是矩阵乘法中逐元素相乘的过程，沿特征求和就是矩阵乘法中对这些相乘元素求和的过程
        #不过这个虽然我或许是搞懂了，但要我自己整出这个玄学Parameter那是不太可能……我搞不出来的
        alpha_r = (x_r * self.att_r).sum(axis=-1)
        
        out = self.propagate(edge_index, x=(x_l, x_r), alpha=(alpha_l, alpha_r),size=size)  #[N,H,C]
        out = out.view(-1, H * C)  #[N,d=H*C]
        
        return out


    def message(self, x_j, alpha_j, alpha_i, index, ptr, size_i):
    	#alpha：[E,H]
    	#x:[N,H,C]
    	#那个ptr和index反正是那个我看不懂的softmax里面的参数

		#步骤：
        #在message而非aggregate函数中应用attention
        #attention coefficient=LeakyReLU(alpha_i+alpha_j)
        #attention weight=softmax(attention coefficient)（就这两步都是alpha，就在代码里没区分e和alpha）
        #embeddings * attention weights
        
        alpha = alpha_i + alpha_j
        alpha = F.leaky_relu(alpha,self.negative_slope)
        alpha = softmax(alpha, index, ptr, size_i)
        #这个softmax是PyG而非torch的内置函数
        #但是反正参数是这些参数
        #可参考：
        #https://pytorch-geometric.readthedocs.io/en/latest/modules/utils.html#torch-geometric-utils
        #https://github.com/rusty1s/pytorch_geometric/blob/master/torch_geometric/utils/softmax.py
        
        alpha = F.dropout(alpha, p=self.dropout, training=self.training).unsqueeze(-1)  #[E,H,1]
        out = x_j * alpha  #[E,H,C]

		return out
		

    def aggregate(self, inputs, index, dim_size = None):
        out = torch_scatter.scatter(inputs, index, dim=self.node_dim, dim_size=dim_size, reduce='sum')
        return out

1.3 建立优化器

（本colab中用于评分的优化器是Adam optimizer）

import torch.optim as optim

def build_optimizer(args, params):
    weight_decay = args.weight_decay
    filter_fn = filter(lambda p : p.requires_grad, params)
    #过滤掉不需要梯度的参数，只将需要计算梯度的参数传入各优化器
    if args.opt == 'adam':
        optimizer = optim.Adam(filter_fn, lr=args.lr, weight_decay=weight_decay)
    elif args.opt == 'sgd':
        optimizer = optim.SGD(filter_fn, lr=args.lr, momentum=0.95, weight_decay=weight_decay)
    elif args.opt == 'rmsprop':
        optimizer = optim.RMSprop(filter_fn, lr=args.lr, weight_decay=weight_decay)
    elif args.opt == 'adagrad':
        optimizer = optim.Adagrad(filter_fn, lr=args.lr, weight_decay=weight_decay)
    if args.opt_scheduler == 'none':
        return None, optimizer
    elif args.opt_scheduler == 'step':
        scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=args.opt_decay_step, gamma=args.opt_decay_rate)
    elif args.opt_scheduler == 'cos':
        scheduler = optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=args.opt_restart)
    return scheduler, optimizer

1.4 构建 train() 和 test() 函数

import time

import networkx as nx
import numpy as np
import torch
import torch.optim as optim

from torch_geometric.datasets import TUDataset
from torch_geometric.datasets import Planetoid
from torch_geometric.data import DataLoader

import torch_geometric.nn as pyg_nn

import matplotlib.pyplot as plt


def train(dataset, args):
    
    print("Node task. test set size:", np.sum(dataset[0]['train_mask'].numpy()))
    #我也不知道为啥它说test set size，但是数训练集的数目，就挺奇怪的，搞不懂
    
    test_loader = loader = DataLoader(dataset, batch_size=args.batch_size, shuffle=True)

    # build model
    model = GNNStack(dataset.num_node_features, args.hidden_dim, dataset.num_classes, 
                            args)
    scheduler, opt = build_optimizer(args, model.parameters())

    # train
    losses = []
    test_accs = []
    for epoch in range(args.epochs):
        total_loss = 0
        model.train()
        for batch in loader:
            opt.zero_grad()
            pred = model(batch)
            label = batch.y
            pred = pred[batch.train_mask]
            label = label[batch.train_mask]
            loss = model.loss(pred, label)
            loss.backward()
            opt.step()
            total_loss += loss.item() * batch.num_graphs
            #这个batch.num_graphs整啥啊，CORA数据集不是就这一张图吗……
        total_loss /= len(loader.dataset)
        losses.append(total_loss)

        if epoch % 10 == 0:
          test_acc = test(test_loader, model)
          test_accs.append(test_acc)
        else:
          test_accs.append(test_accs[-1])
    return test_accs, losses

def test(loader, model, is_validation=True):
    model.eval()

    correct = 0
    for data in loader:
        with torch.no_grad():
            pred = model(data).max(dim=1)[1]
            label = data.y

        mask = data.val_mask if is_validation else data.test_mask
        # node classification: only evaluate on nodes in test set
        pred = pred[mask]
        label = data.y[mask]
            
        correct += pred.eq(label).sum().item()

    total = 0
    for data in loader.dataset:
        total += torch.sum(data.val_mask if is_validation else data.test_mask).item()
    return correct / total
  
class objectview(object):
    def __init__(self, d):
        self.__dict__ = d  #在下一节解释

1.5 训练

呃就是我也不知道怎么会用这种形式来写的，就我也不知道这么写跟直接跑有什么区别。

def main():
    for args in [
        {'model_type': 'GraphSage', 'dataset': 'cora', 'num_layers': 2, 'heads': 1, 'batch_size': 32, 'hidden_dim': 32, 'dropout': 0.5, 'epochs': 500, 'opt': 'adam', 'opt_scheduler': 'none', 'opt_restart': 0, 'weight_decay': 5e-3, 'lr': 0.01},
    ]:
        args = objectview(args)  #见代码下面解释
        for model in ['GraphSage', 'GAT']:
            args.model_type = model

            # Match the dimension.
            if model == 'GAT':
              args.heads = 2
            else:
              args.heads = 1

            if args.dataset == 'cora':
                dataset = Planetoid(root='/tmp/cora', name='Cora')
            else:
                raise NotImplementedError("Unknown dataset") 
            test_accs, losses = train(dataset, args) 

            print("Maximum accuracy: {0}".format(max(test_accs)))
            print("Minimum loss: {0}".format(min(losses)))

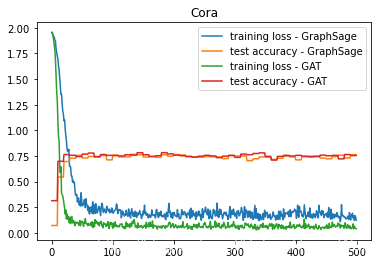
            plt.title(dataset.name)
            plt.plot(losses, label="training loss" + " - " + args.model_type)
            plt.plot(test_accs, label="test accuracy" + " - " + args.model_type)
        plt.legend()
        plt.show()

if __name__ == '__main__':
    main()

就是专门提一下这个objectview函数，就是将args的__dict__属性置为args（就是那个超参字典）。
就是，我试了一下，字典的话就只能靠key来获取value，如 args['model_type']，但是如果用了objectview函数，就可以直接将超参视同args的属性，如可以通过 args.model_type 来获取值。
……
……
……所以我也不知道为什么要专门跑这一步，完全没看出来意义在哪里呢。

输出：
注意这个结果是我修改之前的结果。之所以改了之后就不跑了是因为我报了一个比较邪门的bug导致没法用GPU来跑，就是我也不知道具体是为什么，好像是因为cuda版本不对，但是我觉得我cuda版本是对的。就很邪门一个bug，我不想弄它了。就因为这个很邪门的bug所以我只能用CPU跑，太久了算了。有缘分的话再来研究重跑一遍的事。

Node task. test set size: 140
Maximum accuracy: 0.766
Minimum loss: 0.10853853076696396
Node task. test set size: 140
Maximum accuracy: 0.782
Minimum loss: 0.028875034302473068

可以看出来，在这个任务上是GAT的表现要好一些的。

2. DeepSNAP

DeepSNAP GitHub项目
DeepSNAP 文档

2.1 导包

import torch
import networkx as nx
import matplotlib.pyplot as plt

from deepsnap.graph import Graph
from deepsnap.batch import Batch
from deepsnap.dataset import GraphDataset
from torch_geometric.datasets import Planetoid, TUDataset

from torch.utils.data import DataLoader

2.2 可视化函数

用于可视化NetworkX图格式数据的函数。

def visualize(G, color_map=None, seed=123):
  if color_map is None:
    color_map = '#c92506'
  plt.figure(figsize=(8, 8))
  nodes = nx.draw_networkx_nodes(G, pos=nx.spring_layout(G, seed=seed), \
                                 label=None, node_color=color_map, node_shape='o', node_size=150)
  edges = nx.draw_networkx_edges(G, pos=nx.spring_layout(G, seed=seed), alpha=0.5)
  if color_map is not None:
    plt.scatter([],[], c='#c92506', label='Nodes with label 0', edgecolors="black", s=140)
    plt.scatter([],[], c='#fcec00', label='Nodes with label 1', edgecolors="black", s=140)
    plt.legend(prop={'size': 13}, handletextpad=0)
  nodes.set_edgecolor('black')
  plt.show()

2.3 DeepSNAP的图数据格式

deepsnap.graph.Graph 是DeepSNAP的核心类。
在本colab中将使用NetworkX作为其后台图操作包。

2.3.1 NetworkX图转化示例

创造一个随机的NetworkX图，并将其转换为DeepSNAP图：

num_nodes = 100
p = 0.05
seed = 100

#创建一个随机的NetworkX图G
G = nx.gnp_random_graph(num_nodes, p, seed=seed)

#生成随机的节点特征和节点标签
node_feature = {node : torch.rand([5, ]) for node in G.nodes()}
node_label = {node : torch.randint(0, 2, ()) for node in G.nodes()}

#将节点特征和节点标签赋到G上
nx.set_node_attributes(G, node_feature, name='node_feature')
nx.set_node_attributes(G, node_label, name='node_label')

#打印一个节点作为示例
for node in G.nodes(data=True):
  print(node)
  break

(0, {‘node_feature’: tensor([0.6622, 0.7196, 0.9278, 0.5127, 0.1430]), ‘node_label’: tensor(0)})

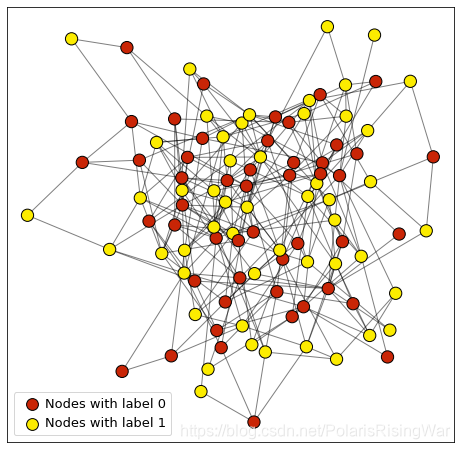
可视化G

color_map = ['#c92506' if node[1]['node_label'].item() == 0 else '#fcec00' for node in G.nodes(data=True)]
visualize(G, color_map=color_map)

将NetworkX图G转换为DeepSNAP图graph

graph = Graph(G)
print(graph)

Graph(G=[], edge_index=[2, 524], edge_label_index=[2, 524], node_feature=[100, 5], node_label=[100], node_label_index=[100])

DeepSNAP会将节点属性转化为Tensor

print("Node feature (node_feature) has shape {} and type {}".format(graph.node_feature.shape, graph.node_feature.dtype))

Node feature (node_feature) has shape torch.Size([100, 5]) and type torch.float32

print("Node label (node_label) has shape {} and type {}".format(graph.node_label.shape, graph.node_label.dtype))

Node label (node_label) has shape torch.Size([100]) and type torch.int64

DeepSNAP还会创造edge_index这一Tensor
（当然按照惯例这个无向图的edge_index的第二维度长度会是边数的两倍，不赘了）

print("Edge index (edge_index) has shape {} and type {}".format(graph.edge_index.shape, graph.edge_index.dtype))

Edge index (edge_index) has shape torch.Size([2, 524]) and type torch.int64

DeepSNAP还能追溯到后台的NetworkX图

print("The DeepSNAP graph has {} as the internal manupulation graph".format(type(graph.G)))

The DeepSNAP graph has <class ‘networkx.classes.graph.Graph’> as the internal manupulation graph

2.4 将PyG数据集转化为一系列DeepSNAP图

root = '/tmp/cora'
name = 'Cora'

# The Cora dataset
pyg_dataset= Planetoid(root, name)

# PyG dataset to a list of deepsnap graphs
graphs = GraphDataset.pyg_to_graphs(pyg_dataset)

# Get the first deepsnap graph (CORA only has one graph)
graph = graphs[0]
print(graph)

Graph(G=[], edge_index=[2, 10556], edge_label_index=[2, 10556], node_feature=[2708, 1433], node_label=[2708], node_label_index=[2708])

2.5 DeepSNAP属性

DeepSNAP具有节点、边、图三种级别的属性。
node_feature node_label
edge_feature edge_label
graph_feature graph_label


通过类属性可获得图基本信息：

1. 节点数：graph.num_nodes
2. 边数：graph.num_edges
3. 标签类数：graph.num_node_labels
4. 特征维度：graph.num_node_features

2.6 DeepSNAP的Dataset

deepsnap.dataset.GraphDataset
官方文档

除了一系列图，还包含这个数据集用于什么任务（task=node / link_pred / graph），以及一些在初始化或其他操作时的实用参数。

示例：以COX2数据集（图级别任务）为例

root = './tmp/cox2'
name = 'COX2'

# Load the dataset through PyG
pyg_dataset = TUDataset(root, name)

# Convert to a list of deepsnap graphs
graphs = GraphDataset.pyg_to_graphs(pyg_dataset)

# Convert list of deepsnap graphs to deepsnap dataset with specified task=graph
dataset = GraphDataset(graphs, task='graph')
print(dataset)

GraphDataset(467)

以打印第一张图为例：

graph_0 = dataset[0]
print(graph_0)

Graph(G=[], edge_index=[2, 82], edge_label_index=[2, 82], graph_label=[1], node_feature=[39, 35], node_label_index=[39], task=[])

2.7 DeepSNAP进阶

2.7.1 导包

import torch
import networkx as nx
import matplotlib.pyplot as plt

from deepsnap.graph import Graph
from deepsnap.batch import Batch
from deepsnap.dataset import GraphDataset
from torch_geometric.datasets import Planetoid, TUDataset

from torch.utils.data import DataLoader

2.7.2 用DeepSNAP进行transductive / inductive的数据集切分

2.7.2.1 Inductive Split

将不同的图切分为训练集 / 验证集 / 测试集。

图分类任务切分数据集示例：

root = './tmp/cox2'
name = 'COX2'

pyg_dataset = TUDataset(root, name)

graphs = GraphDataset.pyg_to_graphs(pyg_dataset)

# Here we specify the task as graph-level task such as graph classification
task = 'graph'
dataset = GraphDataset(graphs, task=task)

# Specify transductive=False (inductive)
dataset_train, dataset_val, dataset_test = dataset.split(transductive=False, split_ratio=[0.8, 0.1, 0.1])

print("COX2 train dataset: {}".format(dataset_train))
print("COX2 validation dataset: {}".format(dataset_val))
print("COX2 test dataset: {}".format(dataset_test))

COX2 train dataset: GraphDataset(373)
COX2 validation dataset: GraphDataset(46)
COX2 test dataset: GraphDataset(48)

2.7.2.2 Transductive Split

在同一张图上进行切分。
默认随机切分数据集，可以通过从PyG加载数据集时直接置 fixed_split=True 或直接修改 node_label_index（应该指的是3种split的 node_label_index 属性）来获取固定的切分。（但是我还没试）

节点分类任务数据集切分示例：

root = '/tmp/cora'
name = 'Cora'

pyg_dataset = Planetoid(root, name)

graphs = GraphDataset.pyg_to_graphs(pyg_dataset)

# Here we specify the task as node-level task such as node classification
task = 'node'

dataset = GraphDataset(graphs, task=task)

# Specify we want the transductive splitting
dataset_train, dataset_val, dataset_test = dataset.split(transductive=True, split_ratio=[0.8, 0.1, 0.1])

print("Cora train dataset: {}".format(dataset_train))
print("Cora validation dataset: {}".format(dataset_val))
print("Cora test dataset: {}".format(dataset_test))

print("Original Cora has {} nodes".format(dataset.num_nodes[0]))

# The nodes in each set can be find in node_label_index
print("After the split, Cora has {} training nodes".format(dataset_train[0].node_label_index.shape[0]))
print("After the split, Cora has {} validation nodes".format(dataset_val[0].node_label_index.shape[0]))
print("After the split, Cora has {} test nodes".format(dataset_test[0].node_label_index.shape[0]))

Cora train dataset: GraphDataset(1)
Cora validation dataset: GraphDataset(1)
Cora test dataset: GraphDataset(1)
Original Cora has 2708 nodes
After the split, Cora has 2166 training nodes
After the split, Cora has 270 validation nodes
After the split, Cora has 272 test nodes

2.7.2.3 边级别的数据集切分

流程：
抽样负边 → 切分正边到训练集 / 验证集 / 测试集 → 将训练集切分为 message passing edges and supervision edges → 在训练阶段重抽样负边等⁹

2.7.2.3.1 All Mode

默认设置

root = '/tmp/cora'
name = 'Cora'

pyg_dataset = Planetoid(root, name)

graphs = GraphDataset.pyg_to_graphs(pyg_dataset)

# Specify task as link_pred for edge-level task
task = 'link_pred'

# Specify the train mode, "all" mode is default for deepsnap dataset
edge_train_mode = "all"

dataset = GraphDataset(graphs, task=task, edge_train_mode=edge_train_mode)

# Transductive link prediction split
dataset_train, dataset_val, dataset_test = dataset.split(transductive=True, split_ratio=[0.8, 0.1, 0.1])

print("Cora train dataset: {}".format(dataset_train))
print("Cora validation dataset: {}".format(dataset_val))
print("Cora test dataset: {}".format(dataset_test))

Cora train dataset: GraphDataset(1)
Cora validation dataset: GraphDataset(1)
Cora test dataset: GraphDataset(1)

message passing edge：edge_index
supervision edge：edge_label_index

print("Original Cora graph has {} edges".format(dataset[0].num_edges))
print("Because Cora graph is undirected, the original edge_index has shape {}".format(dataset[0].edge_index.shape))

print("The training set has message passing edge index shape {}".format(dataset_train[0].edge_index.shape))
print("The training set has supervision edge index shape {}".format(dataset_train[0].edge_label_index.shape))

print("The validation set has message passing edge index shape {}".format(dataset_val[0].edge_index.shape))
print("The validation set has supervision edge index shape {}".format(dataset_val[0].edge_label_index.shape))

print("The test set has message passing edge index shape {}".format(dataset_test[0].edge_index.shape))
print("The test set has supervision edge index shape {}".format(dataset_test[0].edge_label_index.shape))

Original Cora graph has 5278 edges
Because Cora graph is undirected, the original edge_index has shape torch.Size([2, 10556])
The training set has message passing edge index shape torch.Size([2, 8444])
The training set has supervision edge index shape torch.Size([2, 16888])
The validation set has message passing edge index shape torch.Size([2, 8444])
The validation set has supervision edge index shape torch.Size([2, 2108])
The test set has message passing edge index shape torch.Size([2, 9498])
The test set has supervision edge index shape torch.Size([2, 2116])

在all mode中，训练阶段和测试阶段的message passing edge是相同的。
在训练集中，正supervision edges (edge_label_index) 和 message passing edges 是相同的（应该意思是 edge_label_index 同时包含了正负一样多的supervision edges）。
在训练集中，message passing edges 是训练和验证阶段 message passing edges 的加总。
注意，edge_label 和 edge_label_index 这两个属性都是包含负边的。默认负边和正边一样多。

2.7.2.3.2 验证两数据集间是否disjoint

此处disjoint意为两个数据集之间没有相同的边。
不用考虑无向边情况，即认为 (a,b) 和 (b,a) 就是两组边。

函数edge_indices_disjoint，入参为两个数据集的edge_index

def edge_indices_disjoint(edge_index_1, edge_index_2):
  #试过用遍历，特别慢，所以用集合
  
  #代码逻辑是将一个数据集的tuple形式的边储存进集合中
  #然后将第二个数据集的边逐一验证是否在集合中
  edge_set=set()
  for i in range(edge_index_1.shape[1]):
    e=tuple(edge_index_1[:,i].numpy())
    edge_set.add(e)
  for j in range(edge_index_2.shape[1]):
    e=tuple(edge_index_2[:,j].numpy())
    if e in edge_set:
      return False
  disjoint=True
  return disjoint

num_train_edges = dataset_train[0].edge_label_index.shape[1] // 2
train_pos_edge_index = dataset_train[0].edge_label_index[:, :num_train_edges]
train_neg_edge_index = dataset_train[0].edge_label_index[:, num_train_edges:]
print("3.1 Training (supervision) positve and negative edges are disjoint = {}"\
        .format(edge_indices_disjoint(train_pos_edge_index, train_neg_edge_index)))

num_val_edges = dataset_val[0].edge_label_index.shape[1] // 2
val_pos_edge_index = dataset_val[0].edge_label_index[:, :num_val_edges]
val_neg_edge_index = dataset_val[0].edge_label_index[:, num_val_edges:]
print("3.2 Validation (supervision) positve and negative edges are disjoint = {}"\
        .format(edge_indices_disjoint(val_pos_edge_index, val_neg_edge_index)))

num_test_edges = dataset_test[0].edge_label_index.shape[1] // 2
test_pos_edge_index = dataset_test[0].edge_label_index[:, :num_test_edges]
test_neg_edge_index = dataset_test[0].edge_label_index[:, num_test_edges:]
print("3.3 Test (supervision) positve and negative edges are disjoint = {}"\
        .format(edge_indices_disjoint(test_pos_edge_index, test_neg_edge_index)))

print("3.4 Test (supervision) positve and validation (supervision) positve edges are disjoint = {}"\
        .format(edge_indices_disjoint(test_pos_edge_index, val_pos_edge_index)))
print("3.5 Validation (supervision) positve and training (supervision) positve edges are disjoint = {}"\
        .format(edge_indices_disjoint(val_pos_edge_index, train_pos_edge_index)))

3.1 Training (supervision) positve and negative edges are disjoint = True
3.2 Validation (supervision) positve and negative edges are disjoint = True
3.3 Test (supervision) positve and negative edges are disjoint = True
3.4 Test (supervision) positve and validation (supervision) positve edges are disjoint = True
3.5 Validation (supervision) positve and training (supervision) positve edges are disjoint = True

2.7.2.3.3 Disjoint Mode

edge_train_mode=“disjoint”
课程中讲的transuctive链接预测任务切分方式（算了，我也还没搞懂）。

edge_train_mode = "disjoint"

dataset = GraphDataset(graphs, task='link_pred', edge_train_mode=edge_train_mode)
orig_edge_index = dataset[0].edge_index
dataset_train, dataset_val, dataset_test = dataset.split(
    transductive=True, split_ratio=[0.8, 0.1, 0.1])

train_message_edge_index = dataset_train[0].edge_index
train_sup_edge_index = dataset_train[0].edge_label_index
val_sup_edge_index = dataset_val[0].edge_label_index
test_sup_edge_index = dataset_test[0].edge_label_index

print("The edge index of original graph has shape: {}".format(orig_edge_index.shape))
print("The edge index of training message edges has shape: {}".format(train_message_edge_index.shape))
print("The edge index of training supervision edges has shape: {}".format(train_sup_edge_index.shape))
print("The edge index of validation message edges has shape: {}".format(dataset_val[0].edge_index.shape))
print("The edge index of validation supervision edges has shape: {}".format(val_sup_edge_index.shape))
print("The edge index of test message edges has shape: {}".format(dataset_test[0].edge_index.shape))
print("The edge index of test supervision edges has shape: {}".format(test_sup_edge_index.shape))

The edge index of original graph has shape: torch.Size([2, 10556])
The edge index of training message edges has shape: torch.Size([2, 6754])
The edge index of training supervision edges has shape: torch.Size([2, 3380])
The edge index of validation message edges has shape: torch.Size([2, 8444])
The edge index of validation supervision edges has shape: torch.Size([2, 2108])
The edge index of test message edges has shape: torch.Size([2, 9498])
The edge index of test supervision edges has shape: torch.Size([2, 2116])

2.7.2.3.4 训练时每次迭代后重抽样负边

代码示例是2次迭代时输出的训练集和验证集的负边，可以从输出看到确实是不一样的，有重抽样过的。

dataset = GraphDataset(graphs, task='link_pred', edge_train_mode="disjoint")
datasets = {}
follow_batch = []
datasets['train'], datasets['val'], datasets['test'] = dataset.split(
    transductive=True, split_ratio=[0.8, 0.1, 0.1])
dataloaders = {
  split: DataLoader(
    ds, collate_fn=Batch.collate(follow_batch),
    batch_size=1, shuffle=(split=='train')
  )
  for split, ds in datasets.items()
}
neg_edges_1 = None
for batch in dataloaders['train']:
  num_edges = batch.edge_label_index.shape[1] // 2
  neg_edges_1 = batch.edge_label_index[:, num_edges:]
  print("First iteration training negative edges:")
  print(neg_edges_1)
  break
neg_edges_2 = None
for batch in dataloaders['train']:
  num_edges = batch.edge_label_index.shape[1] // 2
  neg_edges_2 = batch.edge_label_index[:, num_edges:]
  print("Second iteration training negative edges:")
  print(neg_edges_2)
  break

neg_edges_1 = None
for batch in dataloaders['val']:
  num_edges = batch.edge_label_index.shape[1] // 2
  neg_edges_1 = batch.edge_label_index[:, num_edges:]
  print("First iteration validation negative edges:")
  print(neg_edges_1)
  break
neg_edges_2 = None
for batch in dataloaders['val']:
  num_edges = batch.edge_label_index.shape[1] // 2
  neg_edges_2 = batch.edge_label_index[:, num_edges:]
  print("Second iteration validation negative edges:")
  print(neg_edges_2)
  break

First iteration training negative edges:
tensor([[ 253, 2478, 2559, …, 541, 1078, 815],
[ 88, 1827, 2098, …, 2234, 1832, 114]])
Second iteration training negative edges:
tensor([[2631, 2113, 2693, …, 1990, 2241, 821],
[2699, 2557, 1234, …, 810, 233, 461]])
First iteration validation negative edges:
tensor([[2568, 2657, 1968, …, 508, 2315, 763],
[2135, 818, 1366, …, 1795, 1421, 1999]])
Second iteration validation negative edges:
tensor([[2568, 2657, 1968, …, 508, 2315, 763],
[2135, 818, 1366, …, 1795, 1421, 1999]])

2.7.3 Graph Transformation and Feature Computation

在DeepSNAP中，graph transformation / feature computation 分成两类，一类是在训练前的转换（对整个数据集），一类是在训练过程中的转换（对图的一个batch）。

以下代码示例：用NetworkX后台计算PageRank值，在训练前将该特征赋予整个数据集。

def pagerank_transform_fn(graph):

  # Get the referenced networkx graph
  G = graph.G

  # Calculate the pagerank by using networkx
  pr = nx.pagerank(G)

  # Transform the pagerank values to tensor
  pr_feature = torch.tensor([pr[node] for node in range(graph.num_nodes)], dtype=torch.float32)
  pr_feature = pr_feature.view(graph.num_nodes, 1)

  # Concat the pagerank values to the node feature
  graph.node_feature = torch.cat([graph.node_feature, pr_feature], dim=-1)

root = './tmp/cox2'
name = 'COX2'
pyg_dataset = TUDataset(root, name)
graphs = GraphDataset.pyg_to_graphs(pyg_dataset)
dataset = GraphDataset(graphs, task='graph')
print("Number of features before transformation: {}".format(dataset.num_node_features))
dataset.apply_transform(pagerank_transform_fn, update_tensor=False)
print("Number of features after transformation: {}".format(dataset.num_node_features))

Number of features before transformation: 35
Number of features after transformation: 36

从输出可以发现图特征多了一维，即PageRank特征添加成功。

此外，DeepSNAP还支持后台图数据格式（如NetworkX图）和Tensor表示格式之间修改的同步，如可以仅手动更新NetworkX图，通过指定 update_tensor=True 使Tensor格式自动更新。

2.8 Edge Level Prediction

2.8.1 建立模型

使用DeepSNAP和PyG建立一个链接预测模型。
直接应用PyG内置的SAGEConv模型。

import copy
import torch
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt

from deepsnap.graph import Graph
from deepsnap.batch import Batch
from deepsnap.dataset import GraphDataset
from torch_geometric.datasets import Planetoid, TUDataset

from torch.utils.data import DataLoader

import torch.nn.functional as F
from torch_geometric.nn import SAGEConv

class LinkPredModel(torch.nn.Module):
    def __init__(self, input_dim, hidden_dim, num_classes, dropout=0.2):
        super(LinkPredModel, self).__init__()

        self.conv1 = SAGEConv(input_dim, hidden_dim)
        self.conv2 = SAGEConv(hidden_dim, num_classes)
        self.loss_fn =nn.BCEWithLogitsLoss()
		self.dropout = dropout

    def reset_parameters(self):
        self.conv1.reset_parameters()
        self.conv2.reset_parameters()

    def forward(self, batch):
        node_feature, edge_index, edge_label_index = batch.node_feature, batch.edge_index, batch.edge_label_index
        
        pred=self.conv1(node_feature,edge_index)
        pred=F.relu(pred)
        pred=F.dropout(pred,self.dropout,self.training)
        pred=self.conv2(pred,edge_index)  #[节点数,num_classes]
        sp_edges=pred[edge_label_index]  #[2,supervision边数,num_classes]
        #这个索引感觉还挺tricky的，但是总之就是这么一回事
        source_nodes=sp_edges[0]  #[supervision边数,num_classes]
        destination_nodes=sp_edges[1]
        pred=(source_nodes*destination_nodes).sum(axis=1)
        #点积计算相似性，就相似性越高认为两点之间越有边嘛
        return pred
    
    def loss(self, pred, link_label):
        return self.loss_fn(pred, link_label)

2.8.2 构建 train() 和 test() 函数

from sklearn.metrics import *

def train(model, dataloaders, optimizer, args):
    val_max = 0
    best_model = model

    for epoch in range(1, args["epochs"]):
        for i, batch in enumerate(dataloaders['train']):
            
            batch.to(args["device"])

            model.train()
            optimizer.zero_grad()
            p=model(batch)
            loss=model.loss(p,batch.edge_label.float())  #第二个参数也可以用type_as(pred))，这个写法好tricky啊
            loss.backward()
            optimizer.step()

            log = 'Epoch: {:03d}, Train: {:.4f}, Val: {:.4f}, Test: {:.4f}, Loss: {}'
            score_train = test(model, dataloaders['train'], args)
            score_val = test(model, dataloaders['val'], args)
            score_test = test(model, dataloaders['test'], args)

            print(log.format(epoch, score_train, score_val, score_test, loss.item()))
            if val_max < score_val:
                val_max = score_val
                best_model = copy.deepcopy(model)
    return best_model

def test(model, dataloader, args):
    model.eval()

    score = 0
    
    for batch in dataloader:
        batch.to(args["device"])
        p=model(batch)
        #p=nn.Sigmoid(p)不能直接这样写，因为这是一个Module，不是一个直接可用的方法
        p=torch.sigmoid(p)
        p=p.cpu().detach().numpy()  #这后面跟的一堆是输出让我这么干的……
        label=batch.edge_label.cpu().detach().numpy()
        score+=roc_auc_score(label,p)
    score=score/len(dataloader)
 
    return score

2.8.3 设置超参

args = {
    "device" : 'cuda' if torch.cuda.is_available() else 'cpu',
    "hidden_dim" : 128,
    "epochs" : 200,
}

2.8.4 训练

pyg_dataset = Planetoid('/tmp/cora', 'Cora')
graphs = GraphDataset.pyg_to_graphs(pyg_dataset)

dataset = GraphDataset(
        graphs,
        task='link_pred',
        edge_train_mode="disjoint"
    )
datasets = {}
datasets['train'], datasets['val'], datasets['test']= dataset.split(
            transductive=True, split_ratio=[0.85, 0.05, 0.1])
input_dim = datasets['train'].num_node_features
num_classes = datasets['train'].num_edge_labels

model = LinkPredModel(input_dim, args["hidden_dim"], num_classes).to(args["device"])
model.reset_parameters()

optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9, weight_decay=5e-4)

dataloaders = {split: DataLoader(
            ds, collate_fn=Batch.collate([]),
            batch_size=1, shuffle=(split=='train'))
            for split, ds in datasets.items()}
best_model = train(model, dataloaders, optimizer, args)
log = "Train: {:.4f}, Val: {:.4f}, Test: {:.4f}"
best_train_roc = test(best_model, dataloaders['train'], args)
best_val_roc = test(best_model, dataloaders['val'], args)
best_test_roc = test(best_model, dataloaders['test'], args)
print(log.format(best_train_roc, best_val_roc, best_test_roc))

全部输出不赘。
最好模型的最终结果：

Train: 0.8857, Val: 0.8044, Test: 0.8090

3. 其他正文与脚注中未提及的参考资料

1. cs224w-winter-2021/CS224W_Colab_3.ipynb at main · xieck13/cs224w-winter-2021
2. CS224W_Winter2021/CS224W_Colab_3.ipynb at main · hdvvip/CS224W_Winter2021
3. CS224w/CS224W_Colab_3.ipynb at main · fanyun-sun/CS224w