Every day a leetcode
题目来源:202. 快乐数
解法1:hash
根据几个例子,我们发现只有2种结果:
- 最终会得到1
- 最终进入一个循环
其实得到1后,继续计算(将该数替换为它每个位置上的数字的平方和)也是得到1,相当于进入1的循环。
由此可以看出,计算结果一定得到一个循环。
一个数是否是快乐数,取决于循环的入口是不是1。
我们使用STL容器unordered_map作为哈希表。
代码:
/*
* @lc app=leetcode.cn id=202 lang=cpp
*
* [202] 快乐数
*/
// @lc code=start
class Solution
{
public:
int getNext(int n)
{
int sum = 0;
while (n > 0)
{
int x = n % 10;
sum += x * x;
n /= 10;
}
return sum;
}
bool isHappy(int n)
{
unordered_map<int, bool> umap;
while (n != 1 && umap.find(n) == umap.end())
{
umap.insert(pair<int, bool>(n, true));
n = getNext(n);
}
return n == 1;
}
};
// @lc code=end
结果:
复杂度分析:
解法2:快慢指针
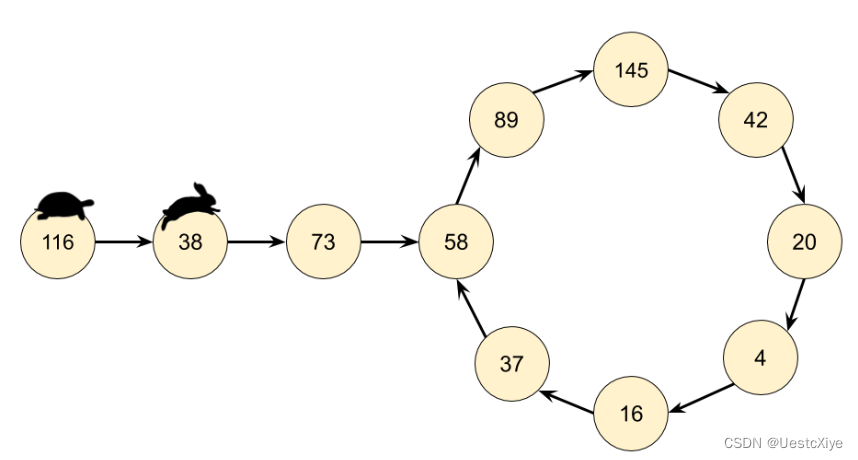
通过反复调用getNext(n)得到的链是一个隐式的链表。隐式意味着我们没有实际的链表节点和指针,但数据仍然形成链表结构。起始数字是链表的头 “节点”,链中的所有其他数字都是节点。next指针是通过调用 getNext(n) 函数获得。
意识到我们实际有个链表,那么这个问题就可以转换为检测一个链表是否有环。因此我们在这里可以使用弗洛伊德循环查找算法。这个算法是两个奔跑选手,一个跑的快,一个跑得慢。在龟兔赛跑的寓言中,跑的慢的称为 “乌龟”,跑得快的称为 “兔子”。
不管乌龟和兔子在循环中从哪里开始,它们最终都会相遇。这是因为兔子每走一步就向乌龟靠近一个节点(在它们的移动方向上)。
使用 “快慢指针” 思想,找出循环:“快指针” 每次走两步,“慢指针” 每次走一步,当二者相等时,即为一个循环周期。此时,判断是不是因为 1 引起的循环,是的话就是快乐数,否则不是快乐数。
注意:此题不建议用集合记录每次的计算结果来判断是否进入循环,因为这个集合可能大到无法存储;另外,也不建议使用递归,同理,如果递归层次较深,会直接导致调用栈崩溃。不要因为这个题目给出的整数是 int 型而投机取巧。
初始化快指针fast为n,慢指针slow为n。
fast = getNext(getNext(fast));
slow = getNext(slow);
最后判断fast是否为1。
代码:
class Solution
{
public:
int getNext(int n)
{
int sum = 0;
while (n > 0)
{
int x = n % 10;
sum += x * x;
n /= 10;
}
return sum;
}
bool isHappy(int n)
{
int fast = n, slow = n;
do
{
fast = getNext(getNext(fast));
slow = getNext(slow);
} while (fast != slow);
return fast == 1;
}
};
结果:
复杂度分析: