题目1:计算布尔二叉树的值
2331. 计算布尔二叉树的值 - 力扣(LeetCode)
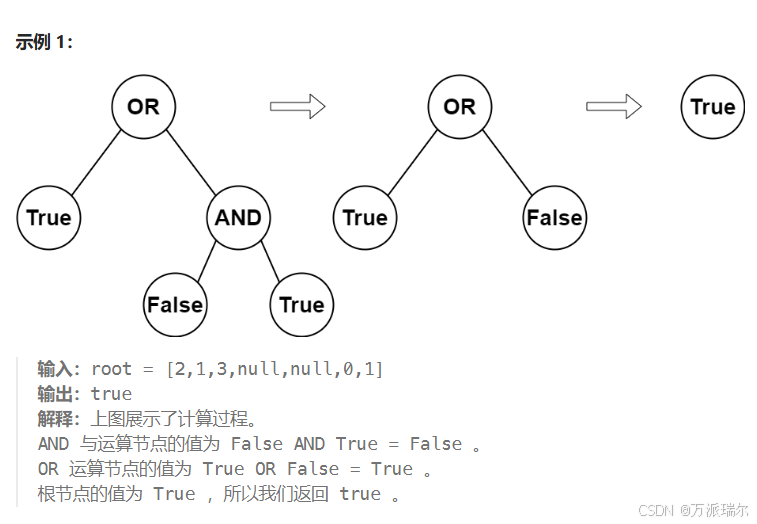
思路:先递归左子树,再递归右子树,将左右子树递归的结果整合然后返回
class Solution {
public boolean evaluateTree(TreeNode root) {
if (root.left == null) {
return root.val == 1 ? true : false;
}
//先计算左边的值
boolean leftRet = evaluateTree(root.left);
//再计算右边的值
boolean rightRet = evaluateTree(root.right);
return root.val == 2 ? leftRet | rightRet : leftRet & rightRet;
}
}
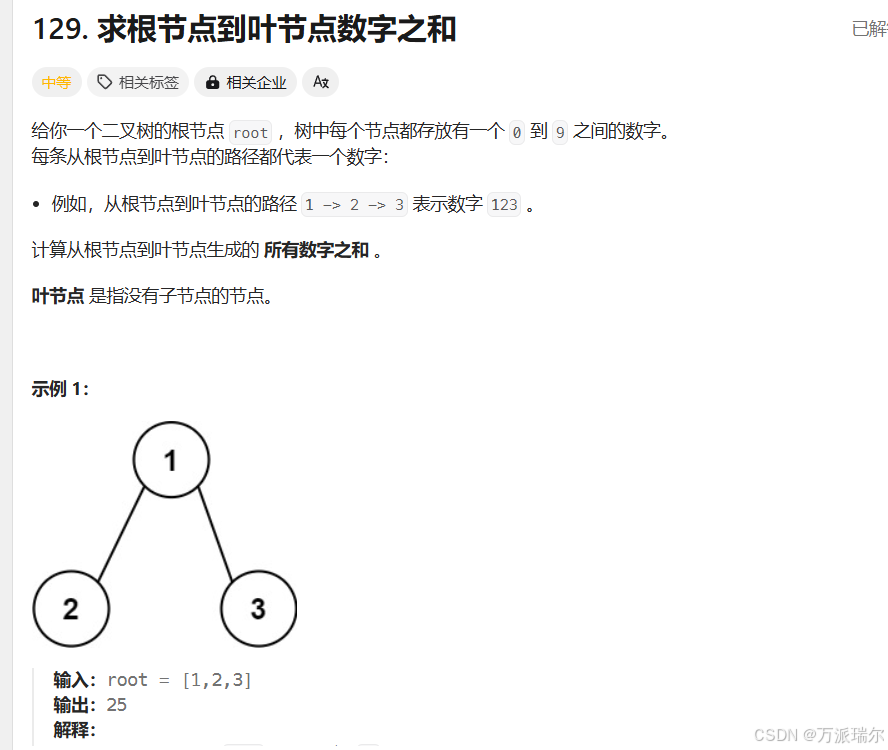
题目2:求根节点到叶子结点数字之和
129. 求根节点到叶节点数字之和 - 力扣(LeetCode)
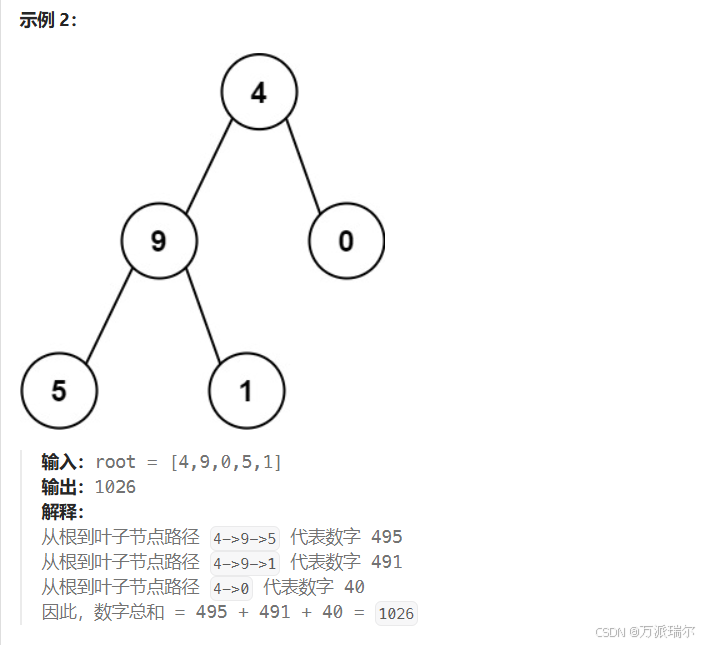
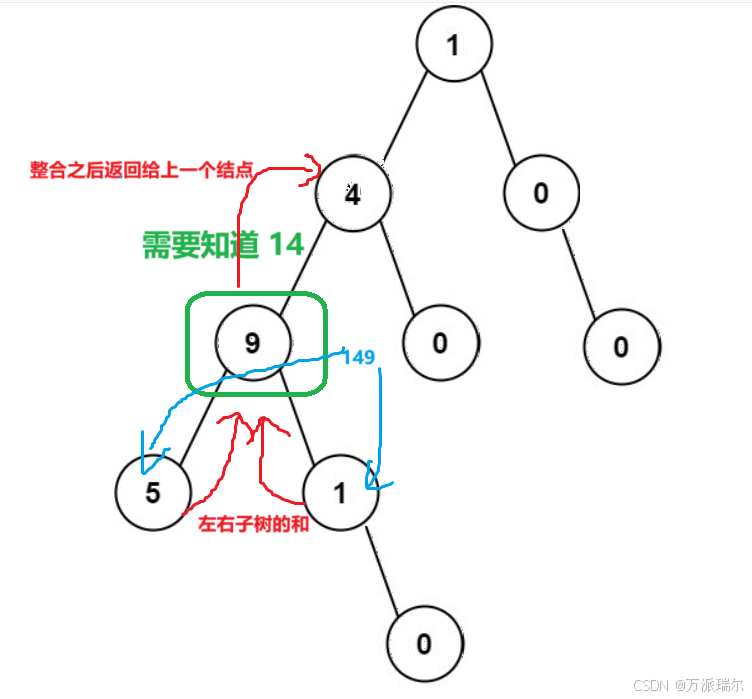
思路:拿中间的某一个小的分支来分析,看看这一步要做什么,以及需要什么
当遍历到图中9这个结点,此时前缀和14是需要知道的,同时14和9相加之后的前缀和,也要交给9结点的左右孩子,计算左右子树的和,将左右子树与根节点的值整合之后,还要返回给4这个结点。因此设计递归函数的时候,参数需要TreeNode以及前缀和,返回值是数字之和
class Solution {
public int sumNumbers(TreeNode root) {
return dfs(root, 0);//根节点,前缀的和为0
}
public int dfs(TreeNode root, int preSum) {
if (root == null) {
return 0;
}
preSum = preSum * 10 + root.val;// 更新前缀和
// 如果是叶子结点,直接返回更新后的前缀和
if (root.left == null && root.right == null) {
return preSum;
}
int ret = 0;
// 计算左边的和
if (root.left != null) {
ret += dfs(root.left, preSum);
}
// 计算右边的和
if (root.right != null) {
ret += dfs(root.right, preSum);
}
return ret;
}
}
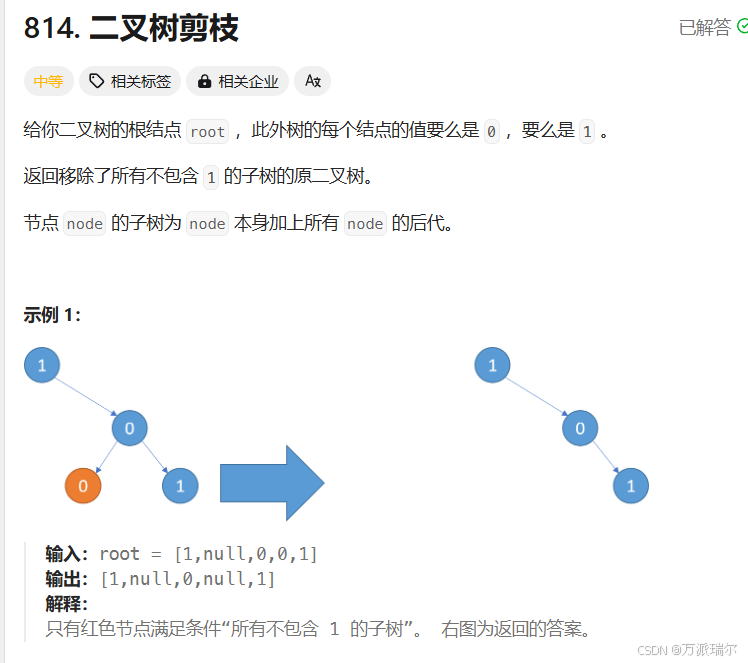
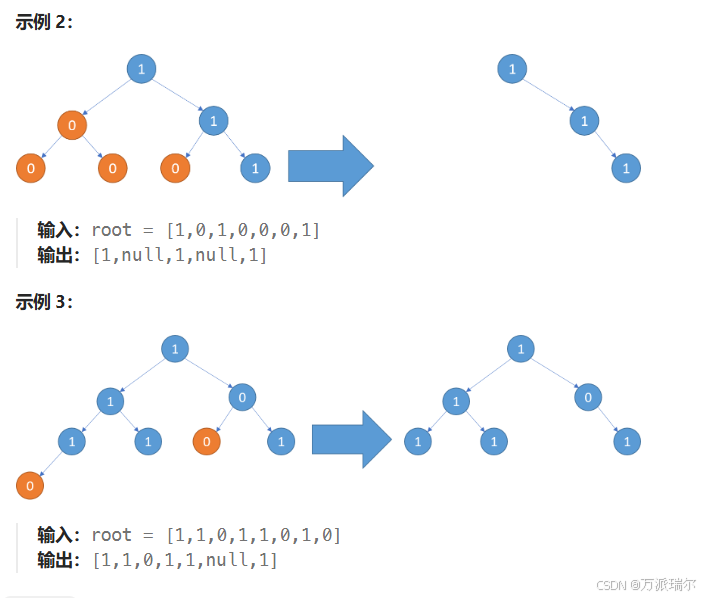
题目3:二叉树剪枝
题目说人话就是:把结点的值全是0的子树给干掉
思路:先处理左子树,再处理右子树,最后返回根结点,如何处理?当遍历到叶子结点时,并且这个叶子结点的值是0,就把这个结点置空,置空后返回,递归的出口:当root为空
class Solution {
public TreeNode pruneTree(TreeNode root) {
return dfs(root);
}
private TreeNode dfs(TreeNode root) {
if (root == null) {
return null;
}
root.left = dfs(root.left);// 左子树处理完之后的值赋值给左结点
root.right = dfs(root.right);// 右子树处理完之后的值赋值给右结点
if (root.left == null && root.right == null && root.val == 0) {
root = null;
return root;
}
return root;
}
}
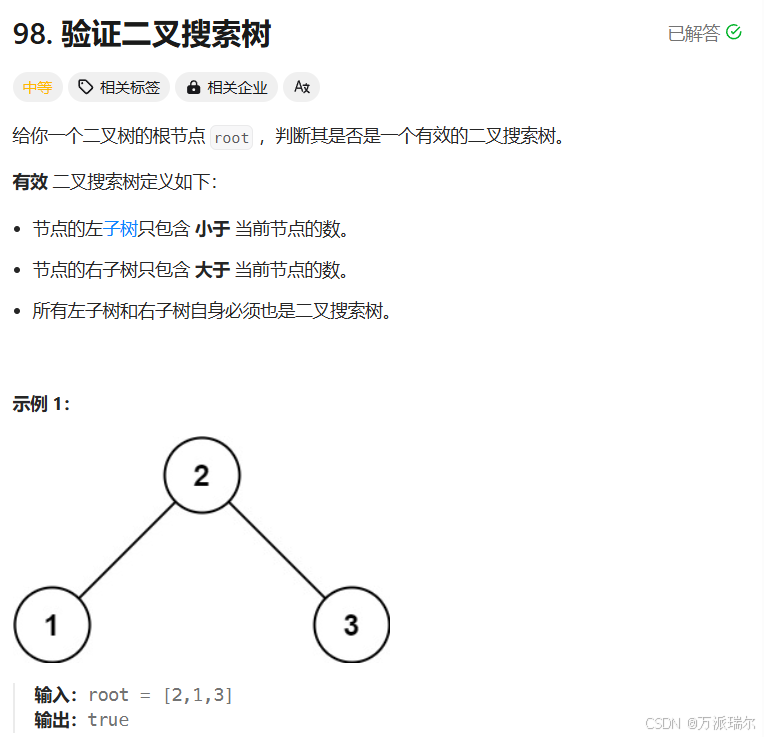
题目4:验证二叉搜索树
关于二叉搜索树有一个结论:二叉搜索树中序遍历的结果是有序的,所以我们可以采取中序遍历的方法,另外定义一个全局变量prev,表示遍历到某一个结点的前驱的值,此时只需比较当前结点的值和这个prev的大小就能知道是否符合二叉搜索树的要求。此外递归过程中,可以进行剪枝,如果左子树都不是二叉搜索树,那么这整个树都不是二叉搜索树,因此右子树就不需要再去递归了,可以直接返回
class Solution {
private long prev = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
return dfs(root);
}
private boolean dfs(TreeNode root) {
if (root == null) {
return true;
}
// 递归左子树
boolean l = dfs(root.left);
// 剪枝
if (l == false) {
return false;
}
// 根
boolean cur = false;
if (prev < root.val) {
cur = true;
prev = root.val;
}
// 剪枝
if (cur == false) {
return false;
}
// 递归右子树右
boolean r = dfs(root.right);
return l && cur && r;
}
}
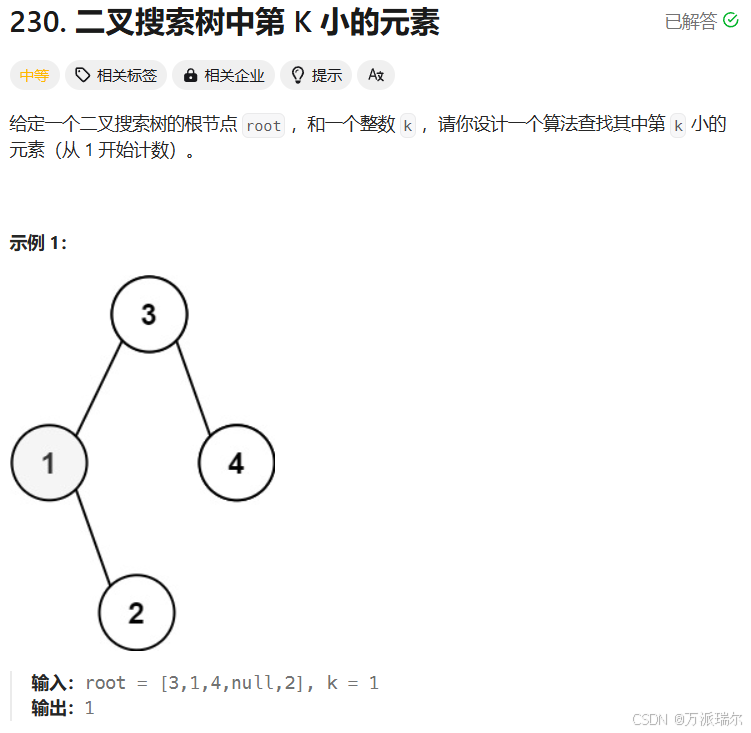
题目4:二叉搜索树中第 K 小的元素
定义两个全局变量,count、ret,count初始值为k,同样的我们采用中序遍历,遍历完结点count就-1,当count为0时,此时当前的结点就是目标值,把这个结点的值赋值给ret然后返回即可
class Solution {
int count = 0;
int ret = 0;
public int kthSmallest(TreeNode root, int k) {
count = k;
dfs(root);
return ret;
}
public void dfs(TreeNode root) {
if(root==null||count==0) {
return;
}
//中序遍历
//左
dfs(root.left);
count--;
if(count==0) {
//如果count=0,说明当前根节点是目标值
ret = root.val;
return;
}
//右
dfs(root.right);
}
}
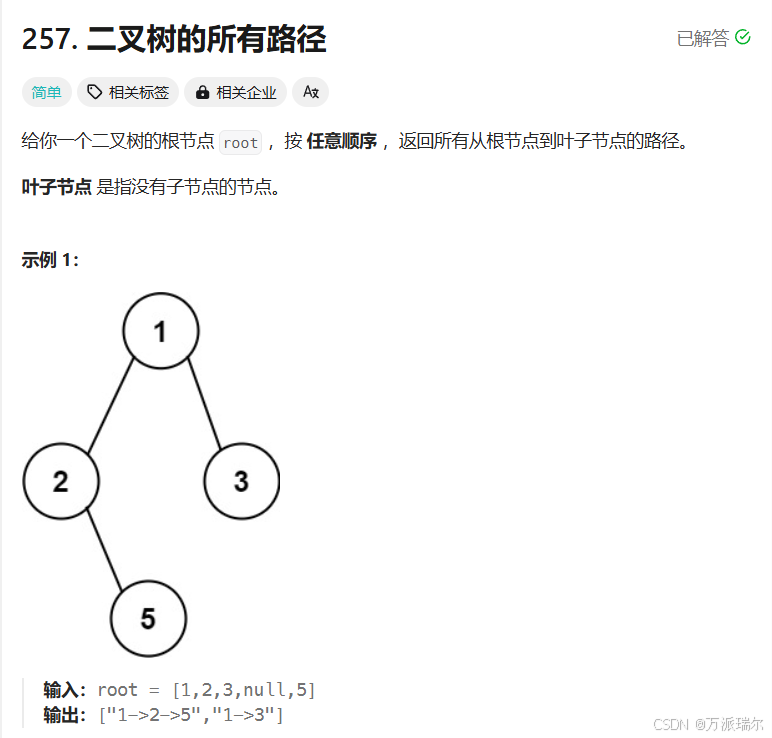
题目5:二叉树的所有路径
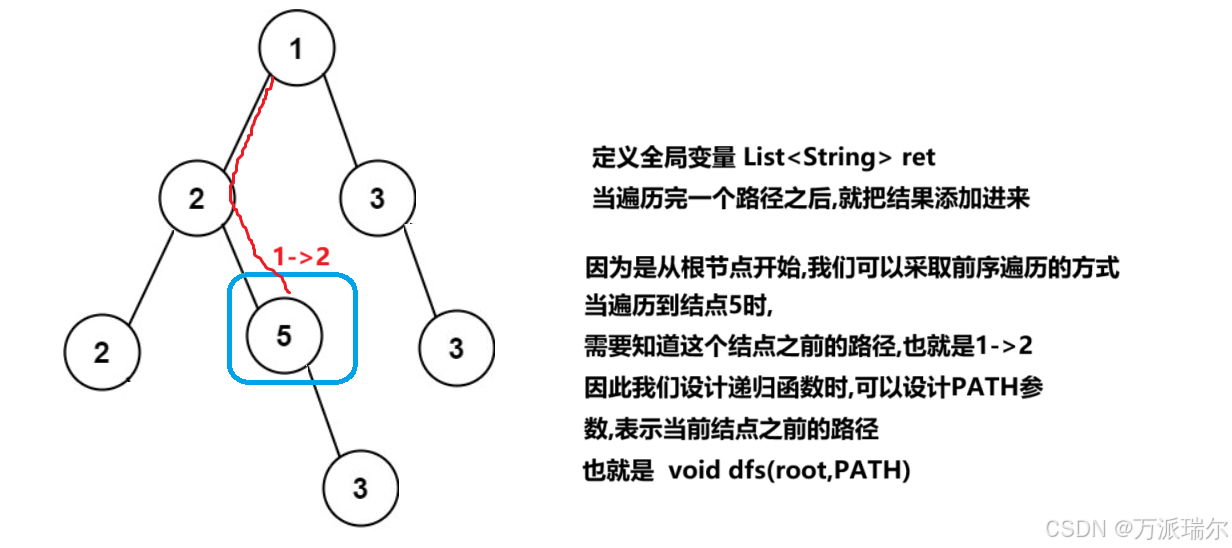
思路:
另外注意一点,如果使用String作为PATH,后续会频繁的进行字符串拼接操作,比较耗时,可以使用StringBuffer
class Solution {
List<String> ret = new ArrayList<String>();
public List<String> binaryTreePaths(TreeNode root) {
StringBuffer sb = new StringBuffer("");
dfs(root, sb);
return ret;
}
public void dfs(TreeNode root, StringBuffer PATH) {
if(root==null) {
return;
}
StringBuffer path = new StringBuffer(PATH);
if (root.left == null && root.right == null) {
path.append(Integer.toString(root.val));
ret.add(path.toString());
return;
}
// path += root.val+"->";
path.append(Integer.toString(root.val));
path.append("->");
dfs(root.left,path);
dfs(root.right,path);
}
}