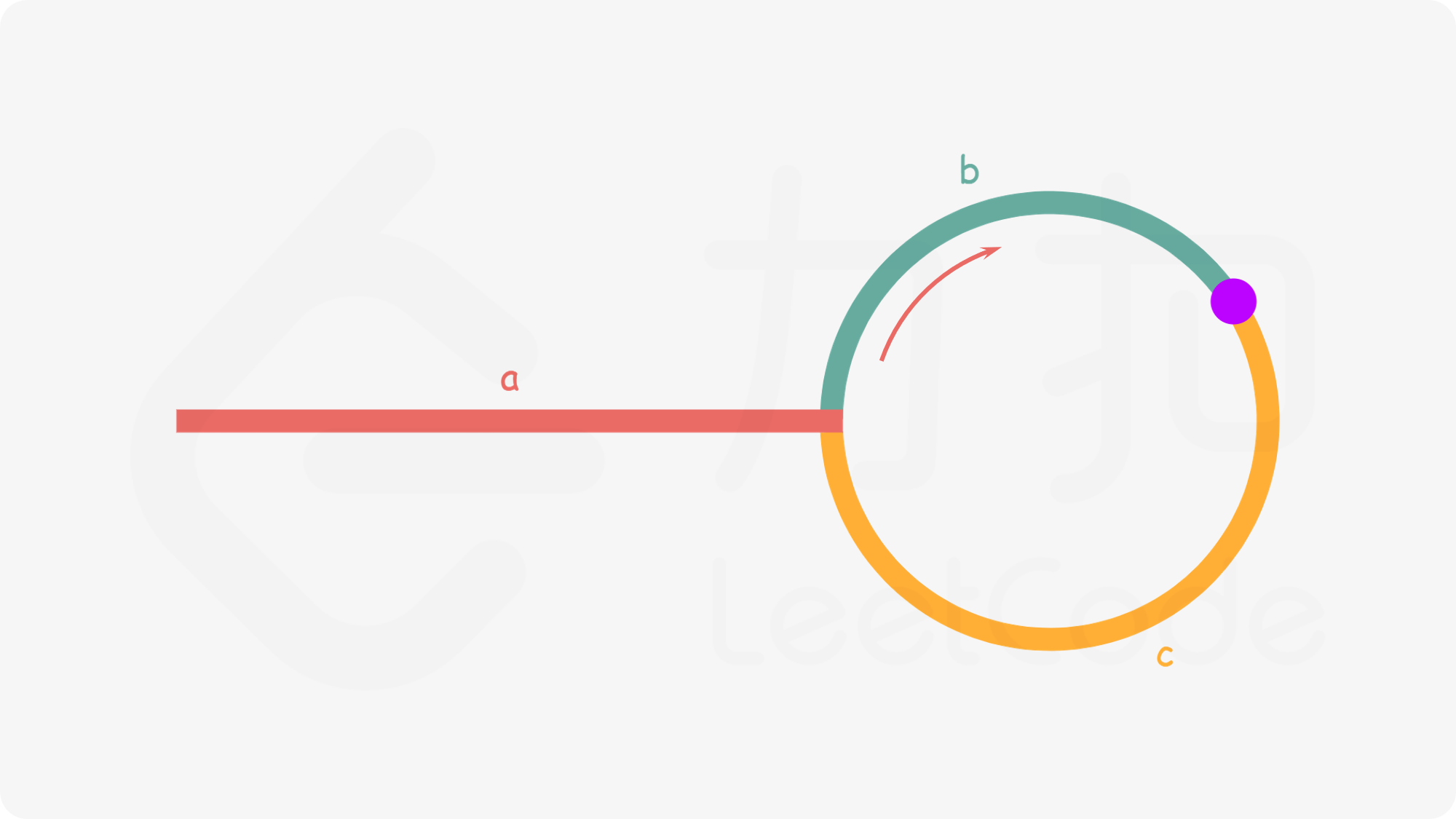11.200.岛屿数量
本题是图论中经典的连通分量问题,可以用bfs/dfs解决。
class Solution {
int[][] directions = new int[][]{
{-1,0},{0,-1},{1,0},{0,1}};
public int numIslands(char[][] grid) {
boolean visited[][] = new boolean[grid.length][grid[0].length];
int result = 0 ;
for(int i = 0 ; i < grid.length ; i++){
for(int j = 0 ; j < grid[0].length ; j++){
if(grid[i][j] == '1' && !visited[i][j]){
visited[i][j] = true;
result++;
dfs(i,j,grid,visited);
}
}
}
return result;
}
public void dfs(int x , int y , char[][] grid , boolean[][] visited){
for(int i = 0 ; i < 4 ; i++){
int nextX = x + directions[i][0];
int nextY = y + directions[i][1];
if(nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) continue;
if(grid[nextX][nextY] == '1' && !visited[nextX][nextY]){
visited[nextX][nextY] = true;
dfs(nextX,nextY,grid,visited);
}
}
}
}使用bfs的话要注意一点:在加入队列的时候做visited标记,而不是在出队列时,否则会造成重复入队。
int[][] directions = new int[][]{
{-1,0},{0,-1},{1,0},{0,1}};
public int numIslands(char[][] grid) {
boolean visited[][] = new boolean[grid.length][grid[0].length];
int result = 0 ;
for(int i = 0 ; i < grid.length ; i++){
for(int j = 0 ; j < grid[0].length ; j++){
if(grid[i][j] == '1' && !visited[i][j]){
visited[i][j] = true;
result++;
bfs(i,j,grid,visited);
}
}
}
return result;
}
public void bfs(int x, int y , char[][] grid, boolean[][] visited){
Deque<int[]> queue = new ArrayDeque<>();
visited[x][y] = true;
queue.add(new int[]{x,y});
while(!queue.isEmpty()){
int[] node = queue.poll();
int nodeX = node[0];
int nodeY = node[1];
for(int i = 0 ; i < 4 ; i++){
int nextX = nodeX + directions[i][0];
int nextY = nodeY + directions[i][1];
if(nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) continue;
if(grid[nextX][nextY] == '1' && !visited[nextX][nextY]){
visited[nextX][nextY] = true;
queue.add(new int[]{nextX,nextY});
}
}
}
}12.198.打家劫舍
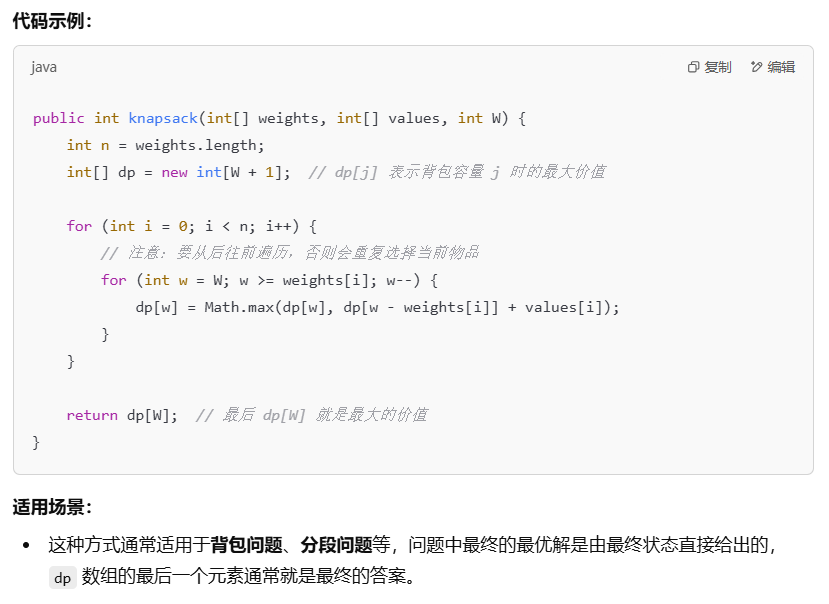
本题是动态规划问题,回顾动态规划五部曲:
(1)确定dp数组及下标含义
(2)确定递推方程
(3)确定如何初始化
(4)确定遍历顺序
(5)dp模拟
(1)dp[i] : 考虑前i家,所能盗取的最大金额
(2)递推方程:结合递推顺序,从前往后递推,dp[i]应该来源于前面已经计算出来的。又因为不能偷盗相邻的房屋,因此对于当前的第i间房屋,分成两种情况考虑:
不偷,那么最大金额为dp[i-1]
偷,那么最大金额为dp[i-2] + nums[i]
二者取最大值,dp[i] = Math.max(dp[i-1] , dp[i-2] + nums[i])
(3)确定如何初始化:根据递推方程,需要初始化dp[0]和dp[1]
根据定义,dp[0] = num[0] , dp[1] = Math.max(dp[0],dp[1])
(4)确定遍历顺序 从前往后遍历
(5)dp模拟
public int rob(int[] nums){
int[] dp = new int[nums.length];
if(nums.length == 1) return nums[0];
dp[0] = nums[0];
dp[1] = Math.max(nums[0],nums[1]);
for(int i = 2 ; i < nums.length ; i++){
dp[i] = Math.max(dp[i-1],dp[i-2] + nums[i]);
}
return dp[nums.length-1];
}13.169.多数元素
(1)简单的统计
public int majorityElement(int[] nums) {
int border = nums.length/2;
int result = 0;
Map<Integer,Integer> map = new HashMap<>();
for (int num : nums) {
map.put(num,map.getOrDefault(num,0)+1);
}
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
int num = entry.getKey();
int cnt = entry.getValue();
if(cnt > border){
result = num;
}
}
return result;
}(2)排序
(3)随机化算法
(4)分治
(5)Boyer-Moore 投票算法
该算法做到了时间复杂度O(n),空间复杂度O(1)
class Solution {
public int majorityElement(int[] nums) {
int count = 0;
Integer candidate = null;
for(int num : nums){
if(count == 0){
candidate = num;
}
count += (num == candidate) ? 1 : -1;
}
return candidate;
}
}以上若干解法在本题的leetcode官方题解中有详细介绍
本题不允许使用除法,同时除法也无法解决0的问题。
(1)前后缀之积
和前面和后面元素有关系的问题,考虑使用前后缀(和接雨水有点神似)
分别用两个数组计算出前缀之积和后缀之积,再相乘,就得到了结果。
这种解法时间上进行了三次顺序遍历,空间上使用了2长度为nums.length的数组,时间复杂度为 O(n),空间复杂度为O(n)
public int[] productExceptSelf(int[] nums) {
int[] pre = new int[nums.length];
int[] sur = new int[nums.length];
pre[0] = 1;
for(int i = 1 ; i < nums.length ; i++){
pre[i] = pre[i-1] * nums[i-1];
}
sur[nums.length-1] = 1;
for(int i = nums.length-2 ; i >= 0; i++){
sur[i] = sur[i+1]*nums[i+1];
}
int[] res = new int[nums.length];
for(int i = 0; i < nums.length ;i++){
res[i] = pre[i] * sur[i];
}
return res;
}进阶要求:在常数空间复杂度内完成题目
前后缀实际上用完了就不再需要了,可以即时地计算使用。
时间复杂度O(n),空间复杂度除了返回结果以外,为O(1)
class Solution {
public int[] productExceptSelf(int[] nums){
int[] res = new int[nums.length];
res[0] = 1;
int pre = 1;
for(int i = 1 ; i < nums.length ; i++){
pre *= nums[i-1];
res[i] = pre;
}
int sur = 1;
for(int i = nums.length-2 ; i >= 0 ; i--){
sur *= nums[i+1];
res[i] *= sur;
}
return res;
}
}或者理解为,在第一轮中直接将pre存储到ans里,第二轮倒着的时候ans直接乘sur。(更进一步的话,pre和sur其实可以用一个变量表示)
15.155.最小栈
(1)使用辅助栈
定义数据栈支持基本的push、pop、top操作
定义辅助栈支持常数时间内确定最小值操作
class MinStack {
Deque<Integer> dataStack;
Deque<Integer> minStack;
public MinStack() {
dataStack = new ArrayDeque<>();
minStack = new ArrayDeque<>();
}
public void push(int val) {
dataStack.push(val);
minStack.push((minStack.isEmpty() || minStack.peek()> val) ? val : minStack.peek());
}
public void pop() {
dataStack.pop();
minStack.pop();
}
public int top() {
return dataStack.peek();
}
public int getMin() {
return minStack.peek();
}
}
/**
* Your MinStack object will be instantiated and called as such:
* MinStack obj = new MinStack();
* obj.push(val);
* obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.getMin();
*/压minStack的时候也可以简化判断逻辑,那么需要实现压入一个Integer.MAX_VALUE作为标志,以防minStack为空
class MinStack {
Deque<Integer> dataStack;
Deque<Integer> minStack;
public MinStack() {
dataStack = new ArrayDeque<>();
minStack = new ArrayDeque<>();
minStack.push(Integer.MAX_VALUE);
}
public void push(int val) {
dataStack.push(val);
minStack.push(( minStack.peek()> val) ? val : minStack.peek());
}
public void pop() {
dataStack.pop();
minStack.pop();
}
public int top() {
return dataStack.peek();
}
public int getMin() {
return minStack.peek();
}
}
/**
* Your MinStack object will be instantiated and called as such:
* MinStack obj = new MinStack();
* obj.push(val);
* obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.getMin();
*/时间复杂度O(1),空间复杂度O(n)
(2)使用一个栈,但是栈保存元素的数据结构不是基础类型,而是本身的值和对应的最小值。相当于把原来两个栈“垂直”合并了。
只需要保持一个当前的min,同时根据push和pop更新min即可。
或者:
时间复杂度O(1),空间复杂度O(n)
(3)自定义一个栈
时间复杂度O(1),空间复杂度O(n)
16.152. 乘积最大子数组
(1)暴力
时间复杂度O(n^2),会时间超限
class Solution {
public int maxProduct(int[] nums) {
int[] product = new int[nums.length];
int res = Integer.MIN_VALUE ;
for(int i = 0 ; i < nums.length ;i++){
product[i] = nums[i];
res = Math.max(res,product[i]);
for(int j = i+1 ; j < nums.length ; j++){
product[j] = product[j-1] * nums[j];
res = Math.max(res,product[j]);
}
}
return res;
}
}(2)动态规划
与最大子序和的递推方程不同的是,这里当前位置的最优解未必是由前一个位置转移得来的,原因在于乘法乘子有负数不是越乘越小的,而加法里的负数是越加越小的。
即负数的乘法具有“逆转”的可能性,基于这种逆转的可能性,我们需要维护一个未来可能逆转为最大值的负数,并且我们希望他“越小越好”(因为这样逆转之后会更大)。从这个角度出发,我们在维护max的同时还要维护一个min.
在max和min的dp方程里,他们交叉存在,这是因为基于当前数字的正负,他们随时有交换逆转的可能。
回顾动态规划五部曲:
(1)确定dp数组及下标含义
dpmax[i]:考虑以i结尾的子数组,能够达到的最大乘积
dpmin[i]:考虑以i结尾的子数组,能够达到的最小乘积
(2)递推方程
dpmax[i] = Math.max(dpmax[i-1]*nums[i],nums[i],dpmin[i-1]*nums[i])
dpmin[i] = Math.min(dp[min[i-1]*nums[i[,nums[i],dpmax[i-1]*nums[i])
(3)初始化
根据递推方程和递推顺序,dpmax[0],dpmin[0]需要初始化
根据dp数组及下标含义,dpmax[0] = dpmin[0] = nums[0];
(4)递推顺序
从前往后
(5)dp模拟
class Solution {
public int maxProduct(int[] nums){
int[] dpmax = new int[nums.length];
int[] dpmin = new int[nums.length];
dpmax[0] = dpmin[0] = nums[0];
for(int i = 1 ; i < nums.length ; i++){
dpmax[i] = Math.max(dpmax[i-1]*nums[i],Math.max(dpmin[i-1]*nums[i],nums[i]));
dpmin[i] = Math.min(dpmin[i-1]*nums[i],Math.min(dpmax[i-1]*nums[i],nums[i]));
}
int res = Integer.MIN_VALUE;
for (int i : dpmax) {
res = Math.max(res,i);
}
return res;
}
}考虑空间优化的话,dpmax,dpmin数组只在从前往后推导的时候用到,并且是相邻用到的,实际上用两个变量(但是由于for循环逻辑里dp递推关系是交叉的,还要区分过去的dpmax和现在dpmax,这里容易混淆)就可以替换。
class Solution {
public static int maxProduct(int[] nums){
int dpmax = nums[0];
int dpmin = nums[0];
int res = nums[0];
for(int i = 1 ; i < nums.length; i++){
int dpmaxCur = Math.max(dpmax*nums[i],Math.max(dpmin*nums[i],nums[i]));
int dpminCur = Math.min(dpmin*nums[i],Math.min(dpmax*nums[i],nums[i]));
res = Math.max(res,dpmaxCur);
dpmax = dpmaxCur;
dpmin = dpminCur;
}
return res;
}
}17.148.排序链表
(1)纯暴力法
遍历了三次O(n),排序O(nlogn),空间复杂度O(n)
总时间复杂度O(nlogn),空间复杂度O(n)
ublic ListNode sortList(ListNode head) {
ListNode node = head;
List<Integer> list = new ArrayList<>();
int size = 0 ;
while(node != null){
size++;
node = node.next;
}
int[] arr = new int[size];
node = head;
int i = 0;
while(node != null){
arr[i++] = node.val;
node = node.next;
}
Arrays.sort(arr);
node = head;
i = 0;
while(node != null){
node.val = arr[i++];
node = node.next;
}
return head;
}(2)进阶要求:你可以在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序吗?
这样就没办法复制链表到数组里排序了,只能从链表自身排序,才能够保持常数级空间复杂度。
对链表本身使用归并排序。
题目:
lastSorted.next = curr.next
curr.next = prev.next
prev.next = curr/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode insertionSortList(ListNode head) {
//判断链表是否为空
if(head == null) return head;
//创建dummyNode 便于在头节点之前插入节点
ListNode dummyNode = new ListNode();
dummyNode.next = head;
//原来控制循环次数的i,现在有cur != null控制
//lastSorted记录有序区的位置
ListNode lastSorted = head;
ListNode cur = head.next;
while(cur != null){
if(cur.val >= lastSorted.val){
lastSorted = lastSorted.next;
}else{
ListNode prev = dummyNode;
while(prev.next.val < cur.val){
prev = prev.next;
}
lastSorted.next = cur.next;
cur.next = prev.next;
prev.next = cur;
}
cur = lastSorted.next;
}
return dummyNode.next;
}
}时间复杂度O(n^2),空间复杂度O(1).
使用插入排序达到了空间复杂度的要求,但没有达到时间复杂度的要求。
用递归法实现归并排序,空间复杂度是O(nlogn);自下而上实现归并排序,空间复杂度是O(1),满足题目要求。
1.递归实现归并排序
这里使用递归法实现归并排序中,使用快慢指针找到中间节点,需要在节点数是偶数的时候选择左边的,因此需要让fast先走一步。否则找到的中间节点是右边的。
如果找到的节点是右边的,这将导致当链表节点只有两个的时候,分割得到的始终是2和0,2的一侧永远是2,无法满足递归终止条件,会StackOverFlow.
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode sortList(ListNode head) {
if(head == null || head.next == null) return head;
ListNode slow = head, fast = head.next;
while(fast != null && fast.next != null){
slow = slow.next;
fast = fast.next.next;
}
ListNode tmp = slow.next;
slow.next = null;
ListNode left = sortList(head);
ListNode right = sortList(tmp);
ListNode h = mergeTwoLists(left, right);
return h;
}
public static ListNode mergeTwoLists(ListNode list1, ListNode list2) {
ListNode newList = new ListNode();
ListNode head = newList;
while(list1 != null && list2 != null){
if(list1.val < list2.val){
head.next = list1;
list1 = list1.next;
}else{
head.next = list2;
list2 = list2.next;
}
head = head.next;
}
head.next = list1 != null ? list1 : list2;
return newList.next;
}
}2.自底向上直接合并 实现归并排序,达到空间复杂度O(1)的要求
将归并排序改造成迭代实现,可以通过一个变量维护需要排序的子链表的长度,这样就知道该在哪里cut、该在哪里merge,当该变量>=链表长度时,排序完成。
class Solution {
public ListNode sortList(ListNode head) {
if (head == null || head.next == null) return head;
// 统计链表长度
int length = 0;
ListNode node = head;
while (node != null) {
length++;
node = node.next;
}
ListNode dummy = new ListNode(0, head);
// 子链表长度,从 1 开始合并,每次翻倍。(这个 for 循环主要是增大两个合并数组的数组长度)
for (int subLength = 1; subLength < length; subLength <<= 1) {
ListNode prev = dummy; // prev 用于连接合并后排序好的链表,相当于记录结果
ListNode cur = dummy.next; // cur 记录拆分链表的位置
// 每次遍历整条链表,将链表拆分成若干个长度为 subLength 的子链表,然后合并。(这个 while 循环才是真正的拆分合并)
while (cur != null) {
// 1. 拆分subLength长度的链表1
ListNode head_1 = cur; // 第一个链表的头节点
// 找到第一个链表的尾结点,拆分出长度为subLength的链表1,
// cur.next != null是为了防止下面的head_2 = cur.next(cur=null报错),或者也可以像下面next一样先判断一下cur != null
for (int i = 1; i < subLength && cur != null && cur.next != null; i++) {
cur = cur.next;
}
// 2. 拆分subLength长度的链表2
ListNode head_2 = cur.next; // 第二个链表的头结点,即链表1尾部的next
cur.next = null; // 断开第一个链表和第二个链表的连接
cur = head_2; // 第二个链表的头节点,重新赋给cur,继续寻找第二个链表的尾结点
// 寻找第二个链表的尾结点,再拆分出长度为subLen的链表2
for (int i = 1; i < subLength && cur != null && cur.next != null; i++) {
cur = cur.next;
}
// 3. 断开第二个链表和剩下链表的连接
ListNode next = null; // next 为剩下链表的头结点(即拆分完两个链表后第二个链表结束位置的next)
// 第二个链表的尾结点可能为空,不为空时才能更新next,所以不能直接 next = cur.next;
if (cur != null) {
next = cur.next;
cur.next = null; // 断开第二个链表和剩下链表的连接
}
// 到这里,已经拆分完毕了,head_1、head_2 都为一条单独的链表,next 为剩下未拆分的链表
// 4. 合并两个subLength长度的有序链表
ListNode merged = mergeTwoLists(head_1, head_2);
prev.next = merged; // prev.next 指向排序好的链表,连接结果
// 将prev移动到subLength × 2 的位置,以连接下一次合并的结果
while (prev.next != null) {
prev = prev.next;
}
cur = next; // 将剩余链表next赋给cur,继续下一次的拆分(循环合并剩下的链表)
}
}
return dummy.next;
}
// 题21. 合并两个有序链表
private ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode(0);
ListNode cur = dummy;
while (l1 != null && l2 != null) {
if (l1.val < l2.val) {
cur.next = l1;
l1 = l1.next;
} else {
cur.next = l2;
l2 = l2.next;
}
cur = cur.next;
}
cur.next = l1 == null ? l2 : l1;
return dummy.next;
}
}(该代码来自leetcode题解评论区,注释详尽)
18.146.LRU缓存
模式识别:出现键和值,且时间复杂度要求O(1),考虑使用哈希表。
为了实现O(1)时间内插入、删除,需要使用双向链表。
为了实现O(1)时间内查找,需要使用到哈希表,且哈希表的key应当存储链表的位置,便于在O(1)时间内定位。
Java中有类似的数据结构,LinkedHashMap,但面试时一般期望面试者自己实现,而不是使用已有的api
class LRUCache extends LinkedHashMap<Integer,Integer>{
private final int capacity;
public LRUCache(int capacity) {
super(capacity,0.75F,true);
this.capacity = capacity;
}
public int get(int key) {
return super.getOrDefault(key,-1);
}
public void put(int key, int value) {
super.put(key,value);
}
@Override
protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
return size() > capacity;
}
}
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache obj = new LRUCache(capacity);
* int param_1 = obj.get(key);
* obj.put(key,value);
*/自定义链表节点实现
class LRUCache {
private int size;
private int capacity;
Map<Integer,DLinkedNode> cache = new HashMap<>();
DLinkedNode head;
DLinkedNode tail;
class DLinkedNode{
DLinkedNode prev;
DLinkedNode next;
int key;
int value;
DLinkedNode(){}
DLinkedNode(int key,int value){
this.key = key;
this.value = value;
}
}
public LRUCache(int capacity) {
this.size = 0;
this.capacity = capacity;
head = new DLinkedNode();
tail = new DLinkedNode();
head.next = tail;
tail.prev = head;
}
public int get(int key) {
DLinkedNode node = cache.get(key);
if(node == null){
return -1;
}else{
removeNode(node);
addToHead(node);
return node.value;
}
}
public void put(int key, int value) {
DLinkedNode node = cache.get(key);
if(node == null){
DLinkedNode newNode = new DLinkedNode(key,value);
cache.put(key,newNode);
addToHead(newNode);
size++;
if(size > capacity){
DLinkedNode tail = removeTail();
cache.remove(tail.key);
size--;
}
}else{
node.value = value;
removeNode(node);
addToHead(node);
}
}
public void removeNode(DLinkedNode node){
node.prev.next = node.next;
node.next.prev = node.prev;
}
public void addToHead(DLinkedNode node){
node.prev = head;
node.next = head.next;
head.next.prev = node;
head.next = node;
}
public DLinkedNode removeTail(){
DLinkedNode node = tail.prev;
removeNode(node);
return node;
}
}
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache obj = new LRUCache(capacity);
* int param_1 = obj.get(key);
* obj.put(key,value);
*/HashMap的查找、链表的增加、删除时间复杂度均为O(1),总的时间复杂度O(1)
空间复杂度O(n)
19.环形链表II
1、使用HashMap记录所有访问到的节点,当遇到第一个重复的节点时,这个节点就是入环结点。
时间复杂度O(n),空间复杂度O(n)
2、快慢指针
快慢指针同时出发,如果有环,最终在环内相遇
假设在紫色处相遇,那么慢指针走了a+b步,快指针走了a+b+n*(b+c)步。
又由于 2*(a+b) = a+b+n*(b+c)
得到 a = (n-1) * (b+c) + c
从相遇点到入环点的距离 再加上若干倍环长,恰好等于从出发点到入环点的距离。那么从相遇开始,派出一个慢指针2从出发点出发,最终两个慢指针会在入环点相遇。
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while(fast != null && fast.next != null){
slow = slow.next;
fast = fast.next.next;
if(fast == slow) {
ListNode slow2 = head;
while(slow != slow2){
slow = slow.next;
slow2 = slow2.next;
}
return slow;
}
}
return null;
}
}20.141.环形链表
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public boolean hasCycle(ListNode head) {
ListNode fast = head, slow = head;
while(fast != null && fast.next != null){
fast = fast.next.next;
slow = slow.next;
if(fast == slow){
return true;
}
}
return false;
}
}