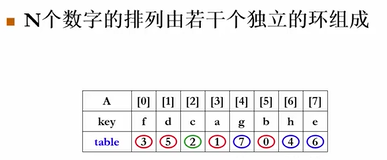
相关群的概念:
对称群(symmetric group),设X是一个集合(可以是无限集),X上的一个双射:a:X→X(即是置换)。集合X上的所有置换构成的族记为S(x),S(x)关于映射的复合运算构成了一个群,当X是有限集时,设X中的元素个数为n,则称群S(x)为n次对称群。
将S(x)的子群统称为变换群(transformation group)。
置换群
一类具体的有限群。有限集合到自身的一一映射称为一个置换。由全排列知识可知,这样的置换共有
n
!
n!
n!个。
研究置换群的性质和构造的理论称为置换群论.凯莱(Cayley,A.)证明:任何一个有限群都同构于一个置换群.因此,可以把一切有限群都看成置换群.由于置换群比抽象群更为直观,而一些数学对象的自同构群是以置换群的面貌出现的,所以,在历史上对置换群的研究先于对抽象群的研究.著名的伽罗瓦理论就是把高次方程的根式可解性的研究转化成为对置换群的研究的,事实上,伽罗瓦(Galois,E.)本人就曾得到有关置换群的一些深刻定理。
特殊的置换:轮换
两个元素的轮换:对换
置换与轮换的性质
(1)如果 [公式] 和 [公式] 是 [公式] 中的两个不相交的轮换,则 [公式]
(2)除恒等置换外, [公式] 中的任何一个置换都可以(不计顺序的意义下)唯一地分解为不相交的轮换的乘积。
(3)任何一个轮换都可以分解为若干个对换的乘积。从而任何一个置换都可以分解为若干个对换的乘积。
(4)任一给定的置换分解为对换的乘积时,无论何种分解方式,得到的对换个数奇偶性不变。
交错群
如果一个置换等于偶数个对换的乘积,则称之为偶置换;否则称为奇置换。所有偶置换构成的集合,按照置换的复合运算构成一个群,称为n次交错群(alternating group),记作 An,则有|An|=n!/2 。
以{1,2,3}为例,集合 [公式] 中的置换有6种情况,读者可以自行列出这6种置换。易知,这6种置换都是轮换,因此可以得到S3={(1),(1,2),(1,3),(2,3),(1,2,3),(1,3,2)}。请注意,(1,2,3) 和 (2,3,1) 还有 (3,1,2) 表示的是同一个置换。
(1,3,2)=(1 2 3;3 1 2)
3次对称群S3是非交换群。事实上,S3是最小的非交换群。
数字华容道
任一给定的置换分解为对换的乘积时,无论何种分解方式,得到的对换个数奇偶性不变。
数字华容道的通解
15数码问题与A*算法
https://github.com/AChep/15puzzle/releases或至谷歌应用商店下载
表排序(现实世界物体的排序)
先编好顺序,
置换
每个环(轮换)只需置换一次