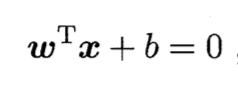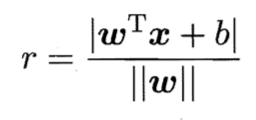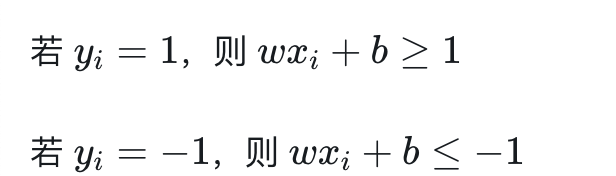支持向量机
0. 本质和概述
0.1 本质
核心:最大化分类间隔的线性分类器(不考虑核函数)
支持向量机(简称SVM)是一种二分类模型,它的基本模型是定义在特种空间上的间隔最大的线性分类器。支持向量机还包括核技巧,这使它成为实质上的非线性分类器。
0.2 概念/术语
-
超平面
不考虑空间维数,二维里的直线、三维里的平面等线性函数统称为超平面。 -
支持向量
在寻找最佳分界线的过程中起了支持作用的数据点。 -
硬间隔、软间隔
硬间隔:正负样本之间的间隔(在这个“隔离带”里面,肯定不会出现任何训练样本)
软间隔:允许个别样本出现在“隔离带”里面在Scikit-Learn的SVM类中,可以通过超参数C来控制这个平衡:
C值越小,边界线比较“软”,间隔带越宽,有一些数据点就可以穿越边界线;若C 很大,边界就会很“硬”,数据点便不能在边界内“生存”
如果SVM模型过度拟合,可以试试通过降低C来进行正则化。
-
决策边界
-
线性分类器
在数学意义上,将线性可分的样本用超平面分隔开的分类模型,叫做线性分类模型,或线性分类器。 -
线性SVM
软间隔的 SVM = 线性 SVM弥补了硬间隔分类的两个主要问题:
- 只在数据是线性可分离的时候才有效;
- 对异常值非常敏感。
小结:
支持向量——决策边界对支持向量位置敏感——缓冲带(软间隔)——惩罚参数(惩罚参数越大,宽容度就越大,缓冲带也就越宽。)
支持向量机其实就是一个边界最大化评估器。
1. 目标函数(损失函数)
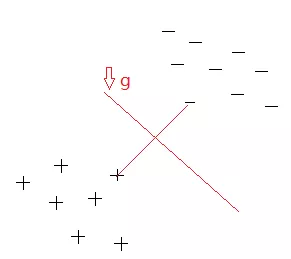
SVM建立决策边界时,只关心距离决策边界最近的那两个样本点,然后取距离它们都最远的决策边g ,认为g就是最佳决策边界。
- 超平面方程
其中 w = (ω1,ω2,… ,ωd) 为法向量决定了超平面的方向 ; b 为位移项,决定了超平面与原点之间的距离。 - 样本空间任意点x到超平面的距离
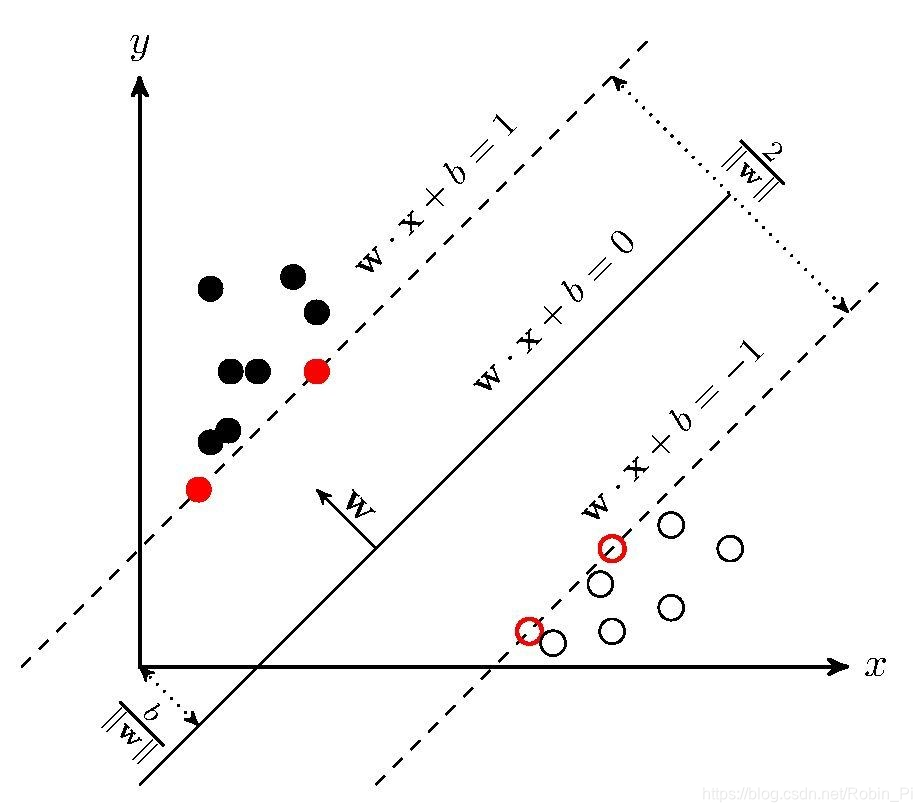
SVM目标函数的结构:max ( r ),即
SVM添加了一个约束,得到的好处是目标函数更精简了:
arg max 1/||w||
s.t., y*f(x)≥1
机器学习中,遇到目标函数求最大值的,都会转化为求最小值,常规套路,SVM也不例外。
它也很简单,分母最小,原式便能最大,即:
arg min ||w||
s.t., y * f(x)>=1
为了后面好算,我们用 (1/2*||w||^2来代替 ||w||,即:
arg min 1/2*||w||2
s.t., y * f(x)>=1
这就是支持向量机的学习目标,其中 min 1/2*||w||2 为目标函数。
注:① 等号右边的1是取的一个值 (为什么这里取 1,因为一般y∈{-1, 1},进一步可以点击
)
② 约束条件的解释:这个条件表示的意思是没有样本点处在超平面1和超平面2中间,且所有点都在正确的那一侧。
上面为约束条件(定义)。
yi 的取值要么是1,要么是-1。yi 为 xi 的标签,当 yi=1 时, xi 为正例;当 yi=−1 时, xi 为负例。
2. 优化算法(求解)
SVM 基本型的目标函数是二次的,约束条件是线性的的凸二次规划问题。
啥是凸?什么是凸优化?
凸优化说的是这么一回事情, X⊂Rn X⊂Rn 为一凸集,f:X→Rf:X→R
为一凸函数,凸优化就是要找出一点x∗∈X,x∗∈X,使得任意x∈X,x∈X,都满足f(x∗)≤f(x)
可以想象成给我一个凸函数,我要去找到最低点。当然凸优化是一个很大很厉害的领域,在这里,我们只需要知晓这个问题是这么一回事。然后,这回事要怎么样求解,就好,有兴趣的朋友可以参考凸优化的概念或者Stephen Boyd & Lieven Vandenberghe 的《Convex Optimization》。
为啥叫二次规划问题呢?
目标函数和约束条件都为变量的线性函数,叫做-----线性规划问题。
目标函数为变量的二次函数和约束条件为变量的线性函数,叫做-----二次规划问题。
目标函数和约束条件都为非线性函数,叫做-----非线性规划问题。
更多参考优秀博文:点击
拉格朗日乘子法
3. SVM软间隔
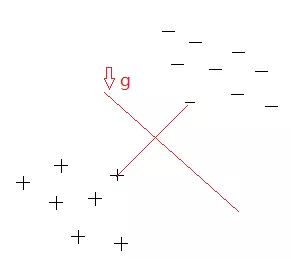
支持向量机能在已知样本点很少情况下,获得很好的分类效果。
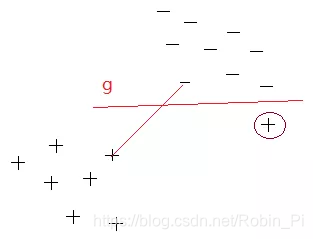
然而,这种对数据点子集的依赖也有缺点,这是因为决策边界对支持向量的位置比较敏感,选取不同的数据点作为训练数据,相应支持向量的位置也不同,而且容易受到噪声点的干扰。(下图,多了一个噪声点会导致产生不好的决策边界)
SVM适当地放宽了约束条件,将 yi*f(xi) >=1,放宽为 yi * f(xi) >=1-ei,这个间隔ei就是软间隔。(它允许一定数量的训练数据点位于错误的一边)
ei在SVM中称为松弛因子,SVM中用控制因子C来控制ei,当C很大时,ei发挥的作用很小,也就是松弛的很小;C很小时,ei发挥的作用很大,可能松弛的作用更强些。
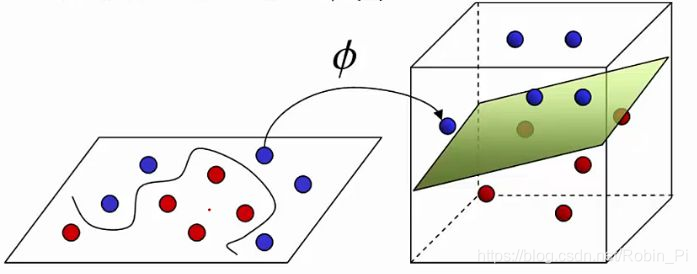
4. 核函数SVM模型
支持向量机还有一个重要的优点是可以使用核函数(Kernel Function)隐式地将样本从原始特征空间映射到更高维的空间, 并解决原始特征空间中的线性不可分问题.
核函数是添加的一个映射,将低维空间下的数据映射到高维下,并且计算的时间复杂度几乎未改变,这是核函数顺利实施的前提。
对于对偶问题中的 xTixj,我们可以将其替换成合适的核函数 k(xTixj),实现非线性数据的高维线性可分。
一般使用以下几种核函数:
序列最小最优化算法SMO可以实现SVM的高效学习。
他将凸二次规划的对偶问题不断的分解为子问题并求解,进而达到求解原问题的目的。
小结:三种支持向量机
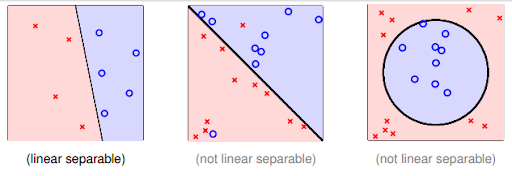
一般支持向量机可以分为三类:
线性可分支持向量机(support vector machine in linearly separable case)、线性支持向量机(linear support vector machine )以及非线性支持向量机(non-linear support vector machine)。
这三个由简至繁的模型分别解决训练数据的三个不同情况。当训练数据线性可分时,训练一个线性可分支持向量机,也称硬间隔支持向量机,当训练数据近似线性可分时,通过软间隔最大化,训练一个线性支持向量机,当数据线性不可分,我们通过核技巧(核技巧由Boser,Guyon等引入)及软间隔最大化学习非线性支持向量机。
5. 代码
5.1 理解 SVM
5.1.1 由来/本质:边界最大化评估器
- 导入模块
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# use seaborn plotting defaults
import seaborn as sns; sns.set()
- 准备数据
from sklearn.datasets.samples_generator import make_blobs # 聚类数据生成器模块
X, y = make_blobs(n_samples=50, centers=2, # 生成50个样本,2类数据
random_state=0, cluster_std=0.60)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn');
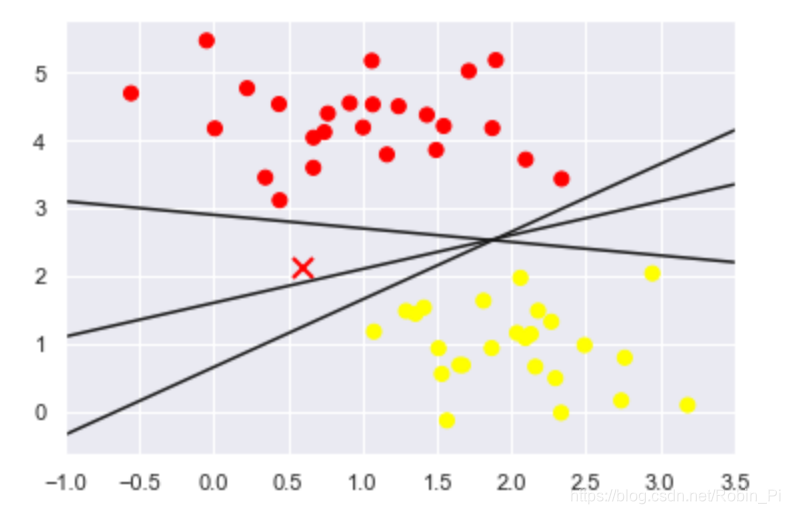
- 尝试普通线性分类器
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn') # 散点图
plt.plot([0.6], [2.1], 'x', color='red', markeredgewidth=2, markersize=10) # 新的数据点
for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]: # 直线参数
plt.plot(xfit, m * xfit + b, '-k')
plt.xlim(-1, 3.5)
问题:
这三个不同的分割器都能完美地判别这些样本,但是选择不同的分割线,可能会让新的数据点分配到不同的标签。
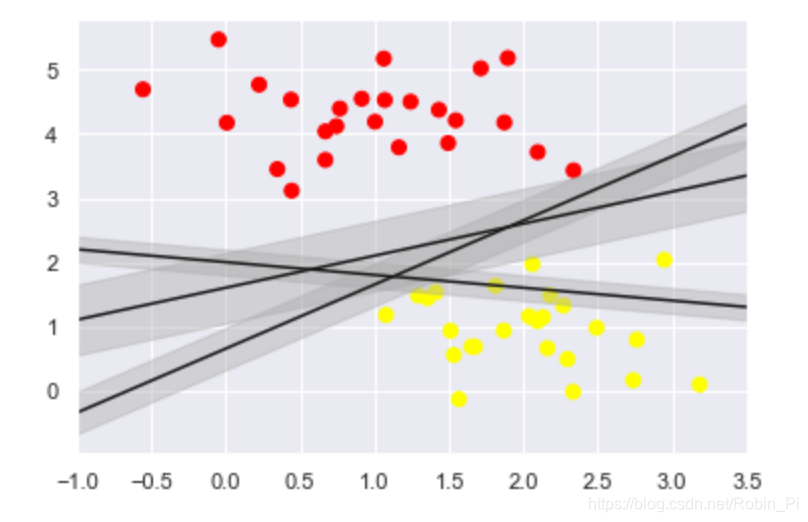
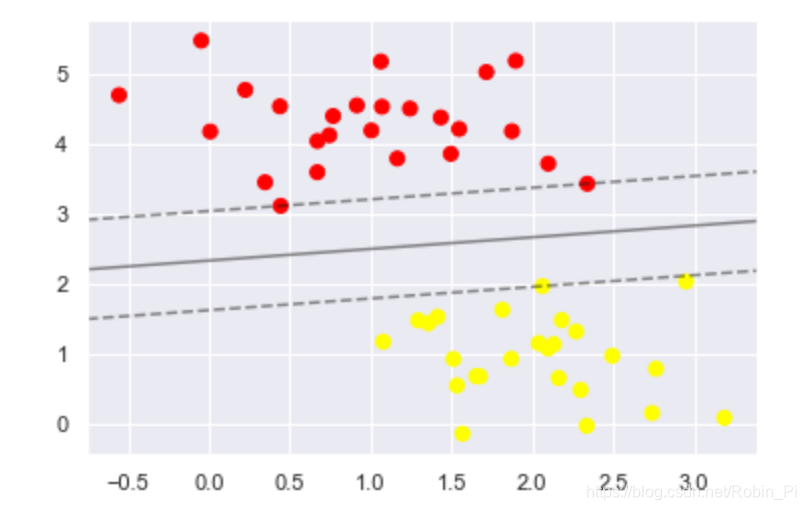
- SVM的解决思路:最大化间隔
# 支持向量机:最大化间隔
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.0, 0.2)]:
yfit = m * xfit + b
plt.plot(xfit, yfit, '-k')
plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5)
支持向量机提供了改进这个问题的方法,它直观的解释是:不再画一条细线来区分类型,而是画一条到最近点边界、有宽度的线条。
在支持向量机中,选择边界最大的那条线是模型最优解。支持向量机其实就是一个边界最大化评估器。
5.1.2 可视化SVM
创建一个辅助函数画出 SVM 的决策边界
def plot_svc_decision_function(model, ax=None, plot_support=True):
"""Plot the decision function for a 2D SVC"""
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
x = np.linspace(xlim[0], xlim[1], 30)
y = np.linspace(ylim[0], ylim[1], 30)
Y, X = np.meshgrid(y, x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)
# plot decision boundary and margins
ax.contour(X, Y, P, colors='k',
levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
# plot support vectors
if plot_support:
ax.scatter(model.support_vectors_[:, 0],
model.support_vectors_[:, 1],
s=300, linewidth=1, facecolors='none');
ax.set_xlim(xlim)
ax.set_ylim(ylim)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(model);
5.2 实例:三个特征的分类
- 模块导入
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
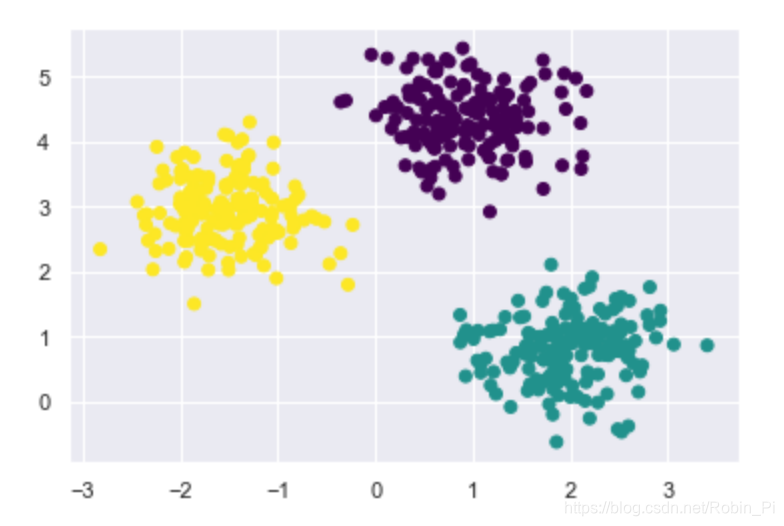
- 准备数据
X, y = make_blobs(n_samples=500, n_features=2, centers=3,
cluster_std=0.5, random_state=0)
print(X.shape)
print(y.shape)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis')
(500, 2)
(500,)
- 拟合模型
svm_model = SVC()
svm_model.fit(X, y)
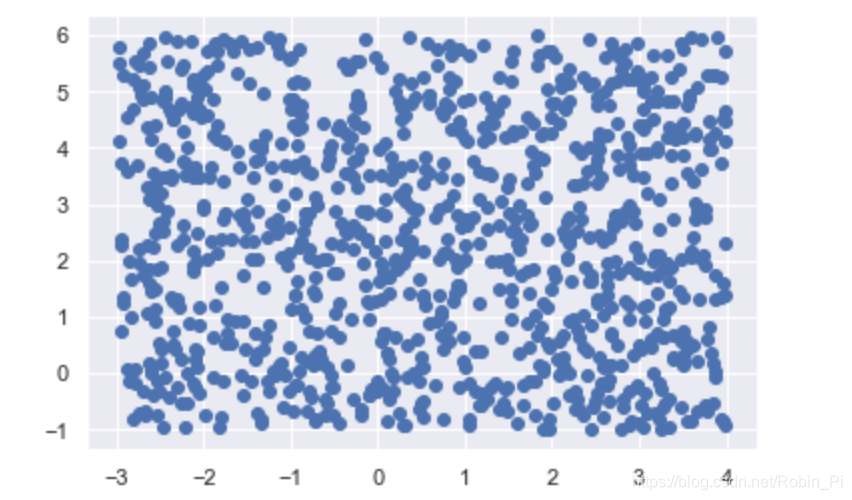
- 新数据 + 预测
# 新数据 + 预测
X_new = [-3, -1] + [7, 7] * np.random.rand(1000, 2)
y_pred = svm_model.predict(X_new)
print(X_new.shape)
print(y_pred.shape)
print(X_new[0:3])
print(y_pred[0:3])
plt.scatter(X_new[:, 0], X_new[:, 1])
(1000, 2)
(1000,)
[[1.99086194 5.70131065]
[0.38723968 2.34514984]
[0.2963255 3.17345496]]
[0 2 0]
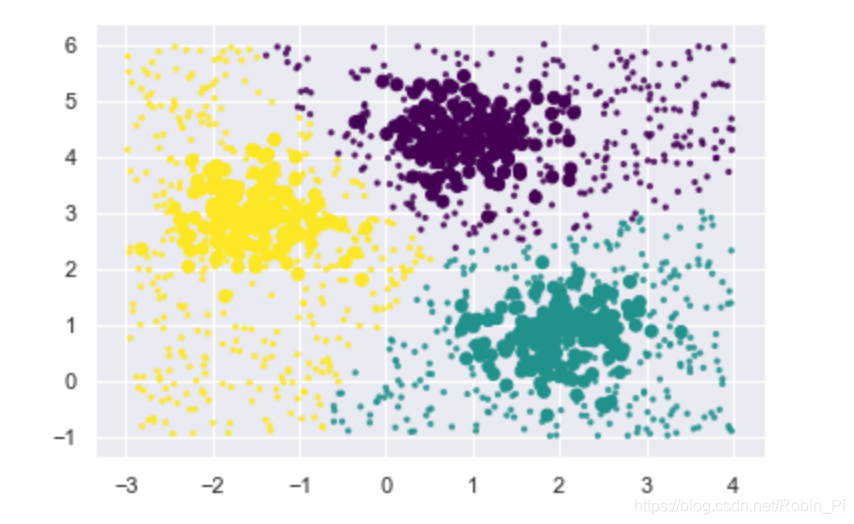
- 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis')
plt.scatter(X_new[:, 0], X_new[:, 1], c=y_pred,
cmap='viridis', s=5, alpha=0.8)
一些疑问
- 为什么不使用函数间隔 margin 而几何间距作为指标
函数间隔、几何间隔、最大间隔分类器
参考: