SVD奇异式分解

SVD是将一个$m\times n$的矩阵分解成三个矩阵的乘积
即$A=U\Sigma V^T$
其中$U,V$分别为$m\times m,n\times nn$的矩阵
$\Sigma$是一个$m\times n$的对角矩阵
其中$U$，是左奇异矩阵，为$A{A}^T$的所有特征向量组成的矩阵，$V$是是右奇异矩阵，为$A^{T}A$的所有特征向量组成的矩阵(按照特征值从大到小排序)
那么奇异值矩阵$\Sigma =U^{-1}AV$

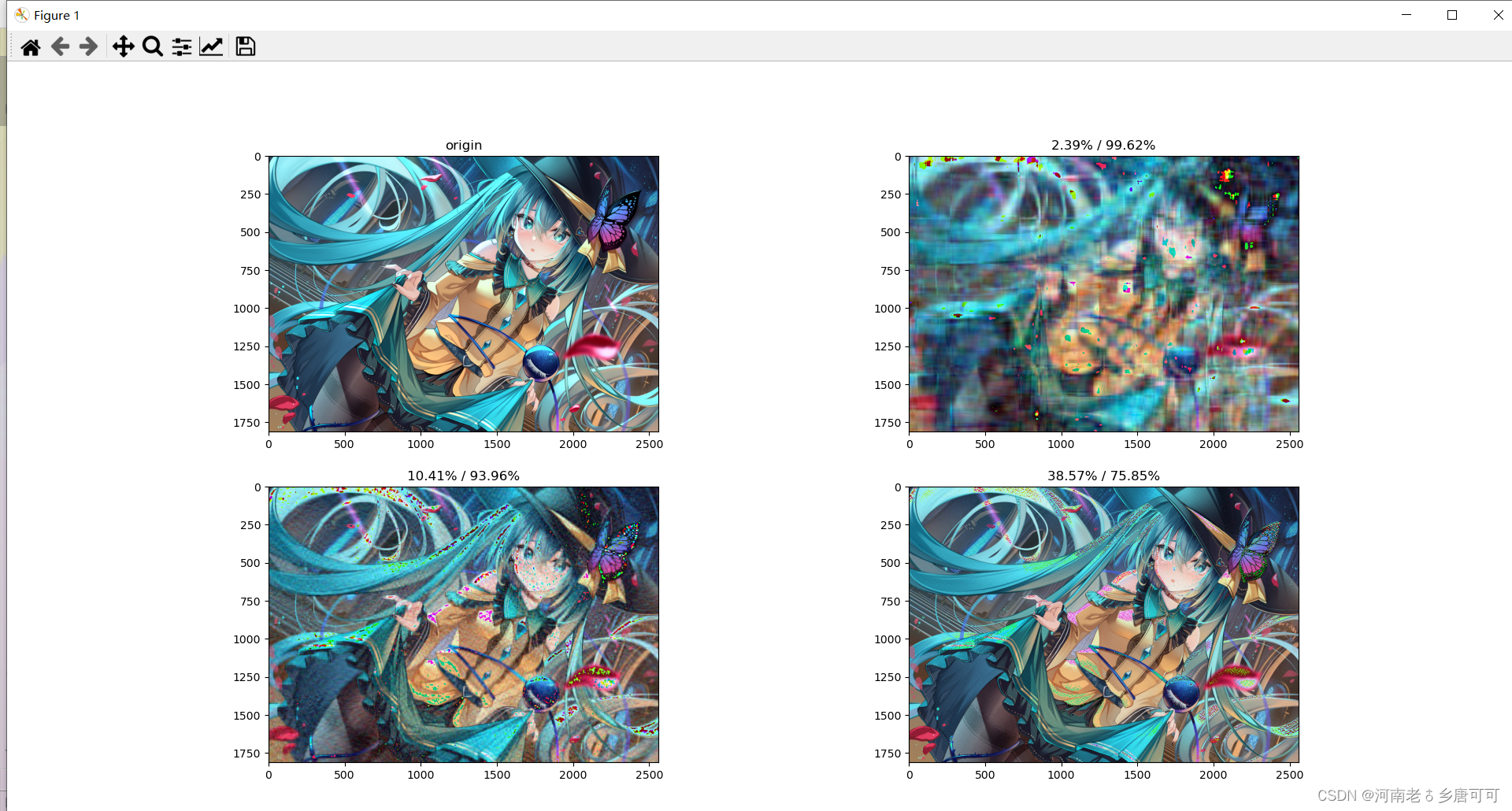
对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：

$$A_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^T\approx U_{m\times k}{\Sigma }_{k\times k}{V}_{k\times n}^T$$

应用在图片压缩中，我们只需要保留分解出的矩阵的前k行（列）的数据，就能够大致还原出图像。
github链接

图片压缩

首先需要明白一点，那就是SVD图片压缩是有损压缩QAQ

那么我们代码思路就是:

1. 载入图片，转化为数值矩阵（R，G，B三种颜色，即三个矩阵，每个像素点的值在[0,255]之间）
2. 对矩阵进行奇异式分解
3. 删除矩阵后面一些行（列），即实现图片压缩
4. 再把删除数据后的矩阵重新相乘，还原图片
5. 计算压缩率，还原程度

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
import pylab

def loadImage(filename): # 1. 载入图片
    image = Image.open(filename)
    return np.array(image)

def svd(A):
    return np.linalg.svd(A)

def reBuildSVD(U, S, V):
    r = len(S)
    return np.dot(U[:,:r] * S, V[:r,:])

def setZero(U, S, V, k): # 把3.部分数据清除
    r = len(S)
    for i in range(k, r):
        U[:, i] = 0
        S[i] = 0
        V[i, :] = 0
    return U, S, V

def totalVariation(S, k): # 计算剩余的数据的比例
    return np.sum(S[:k]) / np.sum(S)

def imageProcess(img, k):
    img2 = np.zeros_like(img) # 构建相同的0矩阵
    tv = 1.0
    for c in range(img.shape[2]): #shape[0]图片高度，shape[1]图片宽度，shape[2]图片通道数(彩色图片是3，即R,G,B)
        A = img[:, :, c]
        U, S, V = svd(A) #2 奇异式分解
        tv *= totalVariation(S, k)
        U, S, V = setZero(U, S, V, k) 
        img2[:, :, c] = reBuildSVD(U, S, V)
    return img2, tv

def Ratio(A, k): #压缩率
    den = A.shape[0] * A.shape[1] * A.shape[2]
    nom = (A.shape[0] * k + k * A.shape[1] + k) * A.shape[2]
    return 1 - nom/den


filname = "./miku.jpg"
miku = loadImage(filname)

plt.figure(figsize=(20, 10))

## 分别放原图，然后从压缩率高往低
#1
plt.subplot(2, 2, 1)
plt.imshow(miku)
plt.title("origin")


# 2
plt.subplot(2, 2, 2)
img, var = imageProcess(miku, 4 ** 2)
ratio = Ratio(miku, 4 ** 1)
plt.imshow(img)
plt.title('{:.2%} / {:.2%}'.format(var, ratio))

# 3
plt.subplot(2, 2, 3)
img, var = imageProcess(miku, 4 ** 3)
ratio = Ratio(miku, 4 ** 3)
plt.imshow(img)
plt.title('{:.2%} / {:.2%}'.format(var, ratio))


# 4
plt.subplot(2, 2, 4)
img, var = imageProcess(miku, 4 ** 4)
ratio = Ratio(miku, 4 ** 4)
plt.imshow(img)
plt.title('{:.2%} / {:.2%}'.format(var, ratio))

pylab.show()

效果

发现压缩率低于$90$%的时候，就能大致还原出图像了
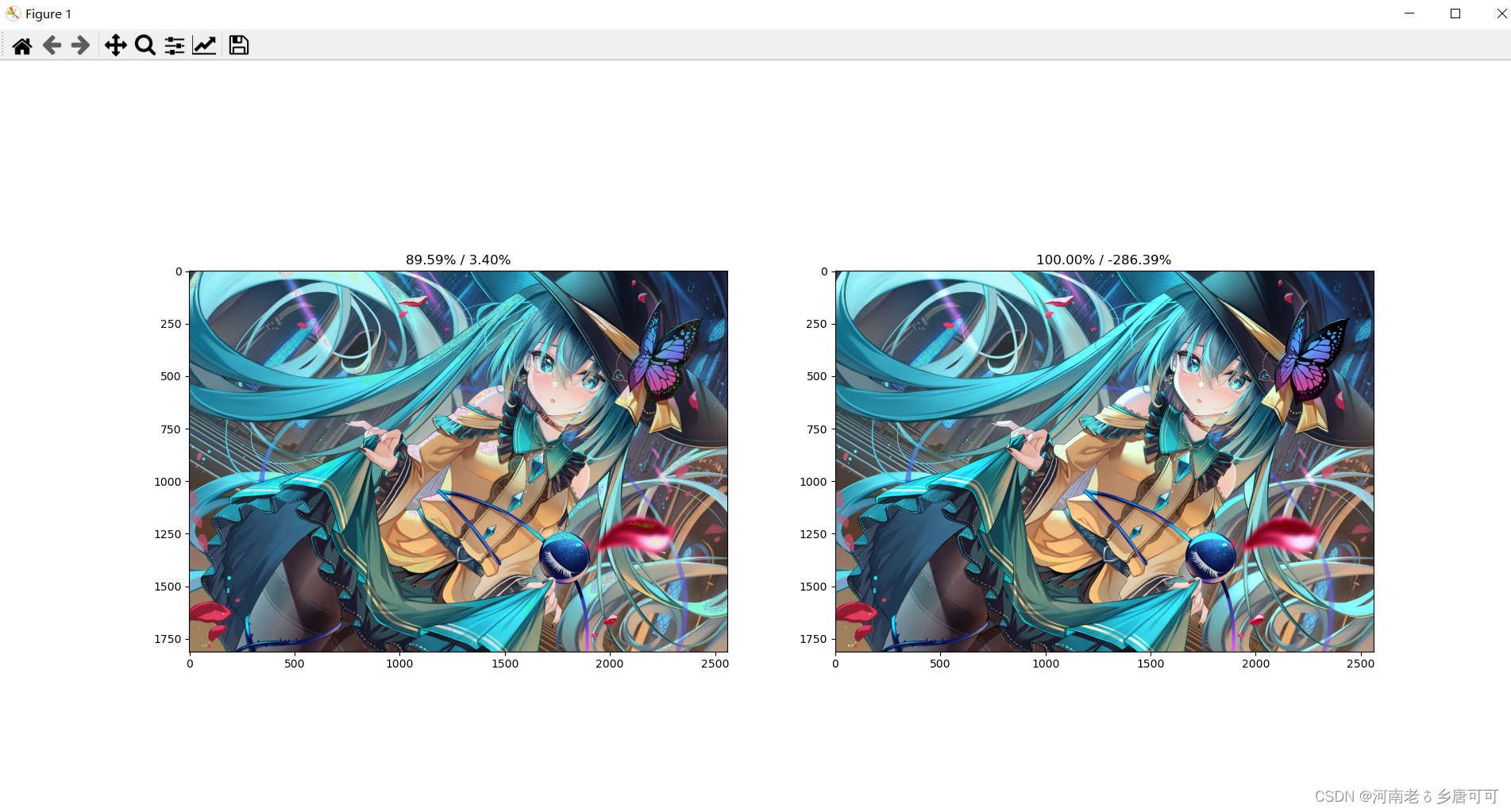
但是想要清晰还原，代价就很大了。甚至还有负压缩（毕竟分解成了三个矩阵）
对二刺螈图片还是别用有损压缩了