机器学习--决策树

决策树模型

决策树基于“树”结构进行决策

· 每个“内部节点”对应于某个属性上的“测试”(test)

` 每个分支对应于该测试的一种可能结果(即该属性的某个取值)

· 每个“叶结点”对应于一个“预测结果”

学习过程：通过对训练样本的分析来确定“划分属性“(即对内部结点所对应的属性)

预测过程：将测试示例从根节点开始，沿着划分属性所构成的”判定测试序列“下行，直到叶结点

决策树基本流程

策略：

“分而治之”(divide-and-conquer)

自根至叶的递归过程

在每一个中间结点寻找一个“划分”(split or test)属性

三种停止条件：

1.当前结点包含的样本全属于同一类别，无需划分 -> 结果为占比较多的类别(把观察到的数据以它的后验概率作为划分)

2.当前属性集为空，或是所有样本在所有属性上取值相同，无法划分->结果为当前属性集类别

3.当前结点包含的样本集合为空，不能划分 -> 结果为父结点中占比较多的类别(把父结点的概率当作以后样本可能的一个先验概率作为划分)

**先验概率 vs 后验概率

先验概率（prior probability）：指根据以往经验和分析。在实验或采样前就可以得到的概率。

后验概率（posterior probability）：是当下由因及果的概率。指某件事已经发生，想要计算这件事发生的原因是由某个因素引起的概率。

其实，先验概率和后验概率的概念是相对的，后验的概率通常是在先验概率的基础上加入新的信息后得到的概率，所以也通常称为条件概率。

决策树算法

基本算法：

属性划分准则

——基于信息量的划分准则

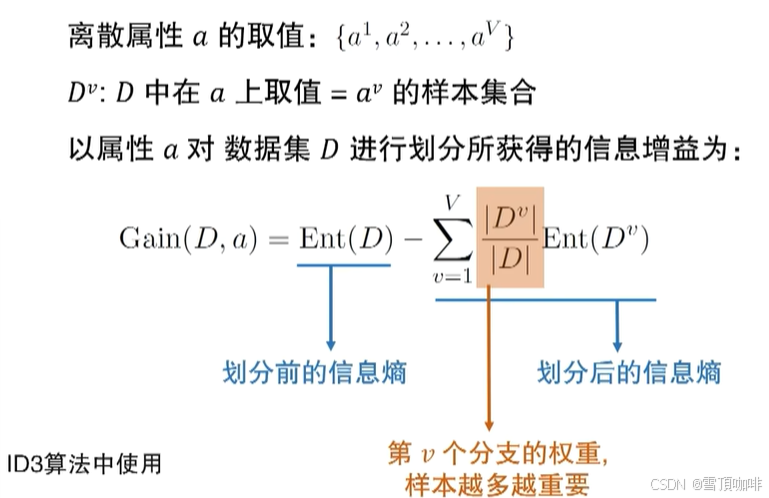
（一）ID3算法 - 以信息增益划分

熵的定义： $P\log_{_{2}}P$

信息熵(entropy)

是度量样本集合“纯度”最常用的一直指标

假定当前样本集合D中第k类样本所占的比例为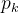 $p_{{k}}$ ,则D的信息熵定义为：

# y为类别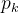， $p_{{k}}$ 为概率，结点的信息熵为该结点所有情况的总和

信息增益(Information Gain)

信息增益直接以信息熵为基础，计算当前划分对信息熵所造成的变化 -> 度量属性划分的价值

->找最优划分属性(信息增益最大的属性)

信息增益的计算：

#划分后的信息熵需乘以分支样本所占权重

## 让信息增益最大化 -> 每一步划分的结果只需要最少的信息就能分干净 -> 只考虑信息量的获得

-> 对可取值数目较多的属性有所偏好，泛化能力较差 (eg.电话号码的划分)

（二）C4.5算法 - 以增益率划分

增益率(Gain Ratio)

C4.5算法中使用

若属性a的可能取值数目越多(即V越大)，则IV(a)的值通常就越大

# Ⅳ(a)实际上是一种规范化(normalizetion)处理

**数据的规范化

规范化的作用：①去掉量纲，使得指标之间具有可比性(即让不可比的东西变得可比)；

②将数据限制到一定区间，使得运算更为便捷。

归一化就是典型的数据规范化方法,归一化即将数据转换到[0,1]的范围

**增益率(Gain Ratio)越高越好？👇

分母： Ⅳ(a)可看成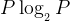 $P\log_{_{2}}P$ (P为分支所占权重) -> 只由分支数造成的熵值减 -> 分支越大，分支数越多，熵值越大 -> 分支越少越好 -> Ⅳ(a)越小越好

分子：信息增益Gain(D,a)越大越好

启发式：

先从后续那划分属性中找出信息增益高于平均水平的，再从中选取增益率最高的

其他属性划分准则

CART算法 - 基于基尼指数(Gini index)的划分

# Gini(D)：所抽取的两个样例不是同一类的概率

划分选择 vs 剪枝

研究表明，划分选择的各种准则虽然对决策时的尺寸有较大影响，但对泛化性能的影响很有限，

剪枝方法和程度对决策树泛化性能的影响更为显著。

**剪枝算法

        剪枝算法的核心思想就是减少网络模型中参数量和计算量，同时尽量保证模型的性能不受影响。

        决策树剪枝的目标是移除不必要的分支，以减少树的复杂性并提高泛化能力。

剪枝方法可以分为以下几种：

        ①基于信息增益的剪枝：在构建决策树时，选择信息增益最高的特征作为分裂基准。当

我们选择信息增益的阈值时，可以通过设置较低的阈值来实现剪枝。
        ②基于复杂度的剪枝：在构建决策树时，为每个节点计算复杂度，并选择复杂度最低的

                特征作为分裂基准。通过设置复杂度阈值，可以实现剪枝。
        ③基于阈值的剪枝：在决策树构建过程中，根据设定的阈值对树进行剪枝，移除信息增

                益或复杂度低于阈值的分支。

决策树的剪枝(pruning)

为什么要剪枝？

为了尽可能正确分类训练样本，有可能造成分支过多 -> 过拟合，所以要对决策树进行“修剪”

## 剪枝(pruning)是决策树对付"过拟合"的主要手段

**过拟合

指的是把训练数据里面不该学的数据的特性错误地当成一般数据

# 通常使用单个决策树的时候，一定是要选择剪枝的

剪枝的基本策略：

· 预剪枝(pre-pruning)：提前终止某些分支的生长

· 后剪枝(post-pruning)：生成一颗完全树，再"回头"剪枝

** 剪枝过程需评估剪枝前后决策树的优劣 => 如何评估？请移步👉《机器学习--模型评估于选择》

缺失值的处理

现实应用中，经常会遇到属性值“缺失”(missing)现象

若仅使用无缺失样例？ -> 对数据的极大浪费

使用带缺失的样例，需解决的问题：

①如何进行属性划分？

②给定划分属性，若样本在该属性上的值缺失，如何进行划分？

基本思路：样本赋权，权重划分

样本赋权

——把样本赋予权重，也可以用其值来作为其权重

权重划分

——把有值的样本进入各个属性的划分结果(后验概率)当作没有值的样本进入分支的先验概率

-> 仅通过无缺失值的样例来判断划分属性的优劣

## 在算总的数据集的信息增益的时候要乘上无缺失值样例占比