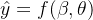什么是神经网络?
“神经网络是由具有适应性的简单单元组成广泛并行互连的网络,它的组织能够模拟生物神经
系统对真实世界物体所作出的交互反应。”
## 神经网络是一个很大的学科领域,此处仅讨论神经网络与机器学习的交集,即“神经网络学习",亦称“连接主义”学习
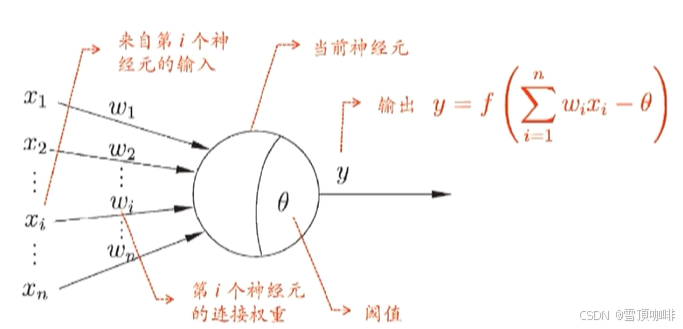
“简单单元”神经元模型
M-P神经元模型
# 神经网络学得的知识蕴藏在连接权和阈值中
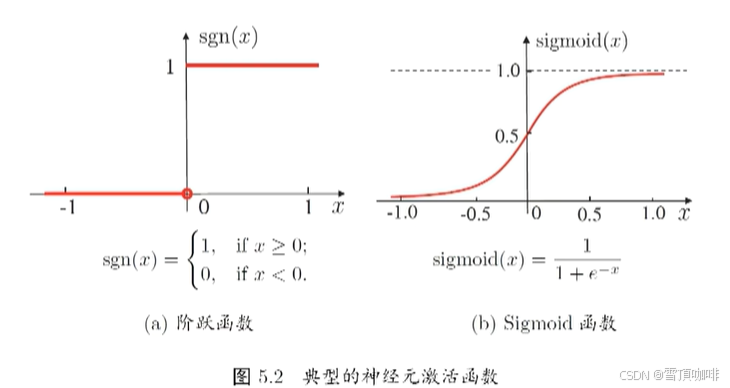
神经元的“激活函数”(Active function)
亦称“响应函数”(给一个数据产生一个输出),“挤压函数”(把负无穷到正无穷的输入挤压到0~1之间)。
# 函数的导数为正负几率的乘积
理想激活函数是介于人函数,0表示一直神经元,而1表示激活神经元
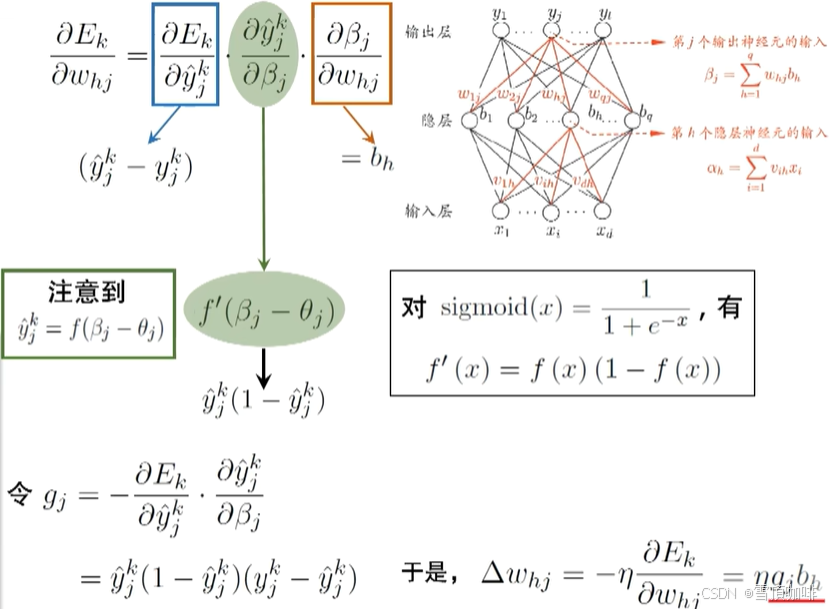
阶跃函数具有不连续、不光滑等不好的性质,常用的是Sigmoid函数
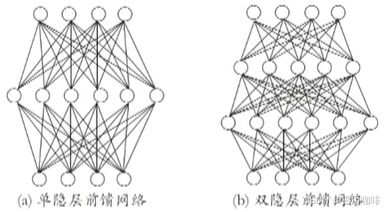
多层前馈网络结构
多层网络
包含隐层的网络
前馈网络
神经元之间不存在同层连接也不存在跨层连接(没有环状的结构)
隐层和输出层神经元亦称“功能单元”(Function Unit)
** 隐层(隐含层):夹在输入和输出神经元(两端)中间的部分
多层前馈神经网络结构如下图👇
万有逼近能力
多层前馈网络有强大的表示能力("万有逼近性")
万有逼近性
仅需一个包含足够多神经元的隐层,多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数
=> 从这个角度来说:任何一个函数逼近问题 ,都可以用单隐层神经网络来解决
-> 延申:任何一个图灵可计算的问题,都可以找到一个神经网络来作为它的求解器
但是,如何设置隐层神经元素是未决问题(Open Problem),现实中常用“试错法”
BP(BackPropagation:误差逆传播算法)
——迄今为止最常用的神经网络算法,可用于多种人物(不仅限于分类)
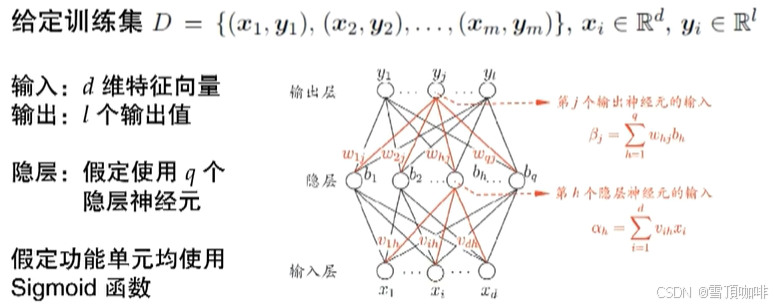
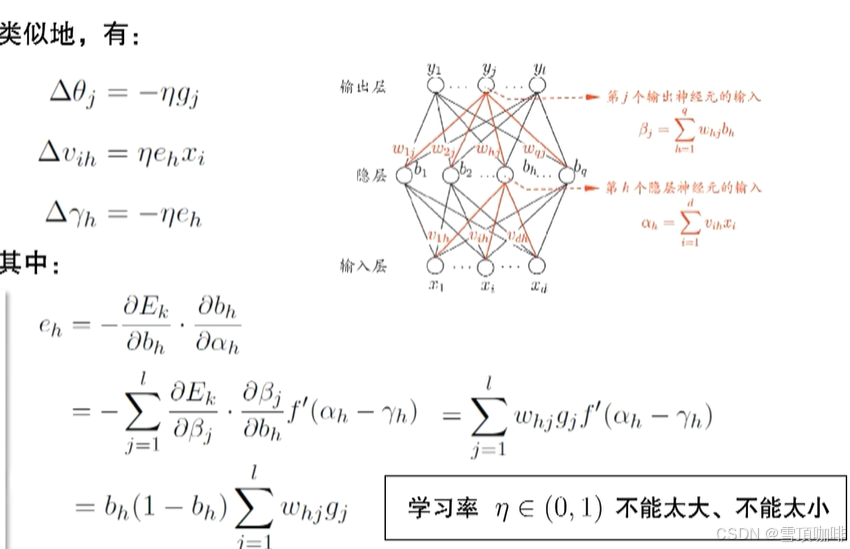
BP算法推导:
#图中为单隐层前馈网络
# β(净输入):等于所有的数加和起来,为了后面表述的方便 ->
# y(输出):ground truth -> (ground truth + error)
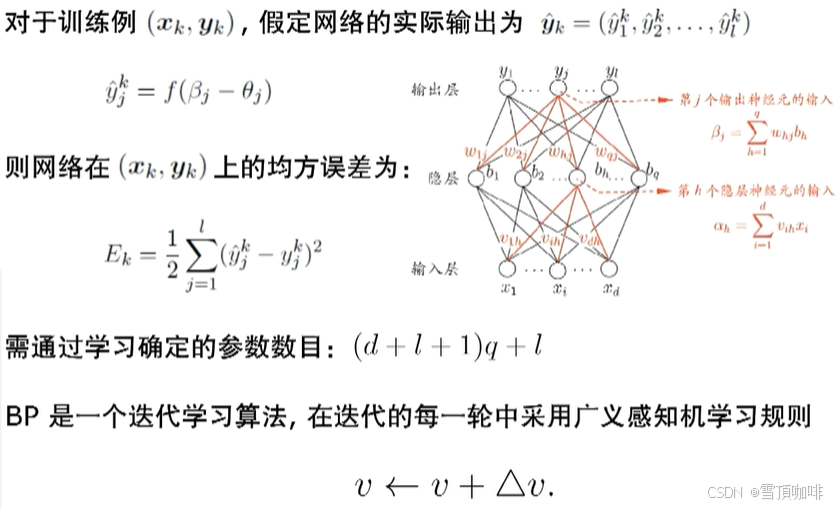
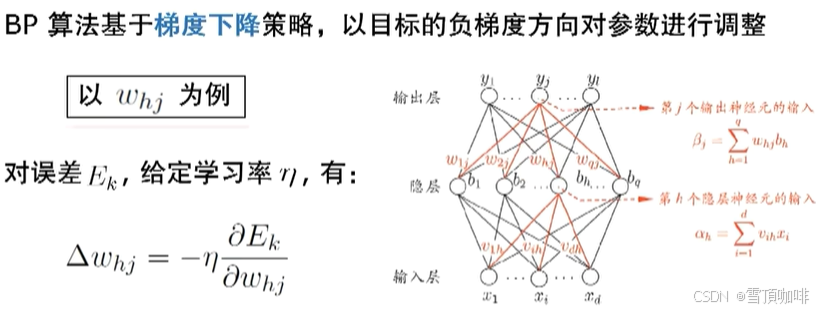
# 梯度:对其求偏导
# η:决定下降的幅度(步长)
# 过程是否收敛取决于训练学习率η
# 振荡:结果一直在不同方向上改变 -> 调整训练的轮数
** η不能太大也不能太小-> Why?👇
η太大时,步长太大 -> 容易产生振荡
η太小时,步长太小 -> 训练时间过长
## 轮(round):学习的轮数,把每一个样本都调过一边为一轮学习