机器学习之逻辑回归原理
1 逻辑回归简介
在机器学习中,逻辑回归在实际上是一种广义线性回归,又略有不同。它同样是求解连续自变量与因变量之间的数学表达式,但这次不用于回归,而是分类。
对于普通的二分类逻辑回归,假设有 n n n个数据, m m m个特征,那么模型公式为:
G ( h w ( x 1 , x 2 . . . x m ) ) = 1 1 + e h w ( x 1 , x 2 . . . x m ) G(h_w(x_1,x_2...x_m)) = \cfrac{1}{1+e^{h_w(x_1,x_2...x_m)}} G(hw(x1,x2...xm))=1+ehw(x1,x2...xm)1
h w ( x 1 , x 2 . . . x m ) = w 0 + w 1 x 1 + w 2 x 2 + . . . w m x m h_w(x_1,x_2...x_m) = w_0+w_1x_1+w_2x_2+...w_mx_m hw(x1,x2...xm)=w0+w1x1+w2x2+...wmxm
2 二元逻辑回归
① sigmoid激活函数
可以看到逻辑回归在基本线性回归的公式上对预测结果进行了非线性变换,这个变换的公式为sigmoid激活函数:
G ( z ) = 1 1 + e z G(z) = \cfrac{1}{1+e^z} G(z)=1+ez1
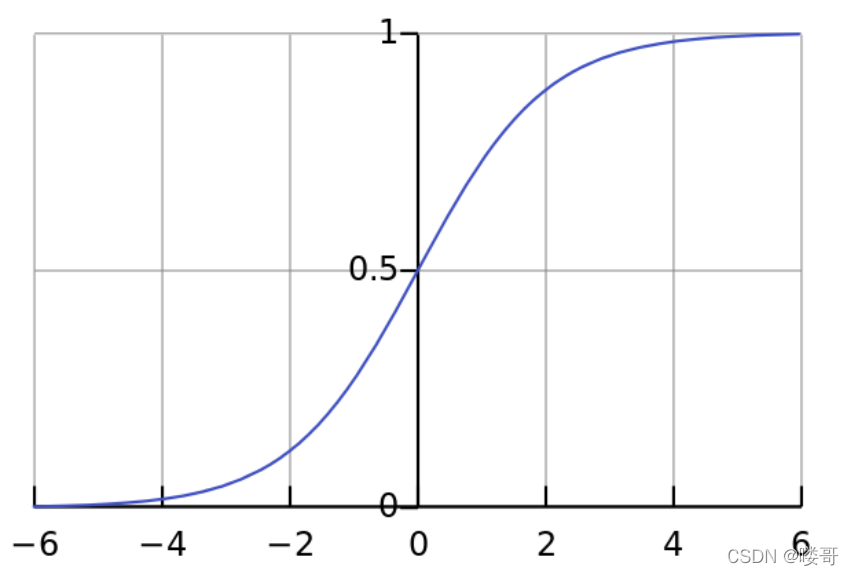
对于为何使用它,这里先放上sigmoid激活函数的图像。
可以看到任何 h w ( x 1 , x 2 . . . x m ) h_w(x_1,x_2...x_m) hw(x1,x2...xm) 的值不管多大大小,在进入 G ( z ) G(z) G(z) 后都会被规整为 ( 0 , 1 ) (0, 1) (0,1) 的区间内。如此针对一个二分类问题,假设类别标签被设置为 0 0 0或 1 1 1,经过该激活函数任何大于等于 0.5 0.5 0.5 的值可被四舍五入归入1类别,小于 0.5 0.5 0.5 则被归入 0 0 0 类别。你可能会有疑问,说我们直接将 h w ( x 1 , x 2 . . . x m ) h_w(x_1,x_2...x_m) hw(x1,x2...xm) 得到的值如果大于等于 0 0 0 就直接归为1类别不就行了,根本用不到激活函数嘛,其实使用激活函数还有一方面是便于损失函数的设计与梯度下降法的迭代。
② 损失函数
逻辑回归损失函数的推导利用的是对数极大似然函数,对于二元逻辑回归,假设类别为1或0,样本数为n(后面为方便推导将 G ( h w ( x 1 , x 2 . . . x m ) ) G(h_w(x_1,x_2...x_m)) G(hw(x1,x2...xm))均写为 G w ( x ) G_w(x) Gw(x)),那么我们有
P ( y = 1 ∣ x ; w ) = G w ( x ) = 1 1 + e h w ( x 1 , x 2 . . . x m ) P(y=1|x;w)=G_w(x)=\cfrac{1}{1+e^{h_w(x_1,x_2...x_m)}} P(y=1∣x;w)=Gw(x)=1+ehw(x1,x2...xm)1
P ( y = 0 ∣ x ; w ) = 1 − G w ( x ) P(y=0|x;w)=1-G_w(x) P(y=0∣x;w)=1−Gw(x)
此时将两个条件概率合并在一起就是
P ( y ∣ x ; w ) = G w ( x ) y ( 1 − G w ( x ) ) 1 − y P(y|x;w)={G_w(x)}^{y}{(1-G_w(x))}^{1-{y}} P(y∣x;w)=