C++---背包模型---有依赖的背包问题（每日一道算法2023.3.24）

注意事项：
本题是"dp动态规划—分组背包"和"背包模型—金明的预算方案"的扩展题，建议先理解，再来做这道会帮助很大。

题目：
有 N 个物品和一个容量是 V 的背包。
物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。

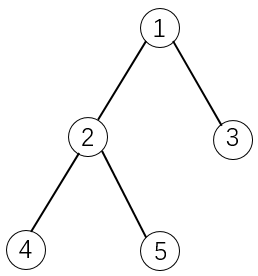
如下图所示：
请添加图片描述
如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。
每件物品的编号是 i，体积是 vi，价值是 wi，依赖的父节点编号是 pi。物品的下标范围是 1…N。
求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行有两个整数 N，V，用空格隔开，分别表示物品个数和背包容量。
接下来有 N 行数据，每行数据表示一个物品。
第 i 行有三个整数 vi,wi,pi，用空格隔开，分别表示物品的体积、价值和依赖的物品编号。
如果 pi=−1，表示根节点。数据保证所有物品构成一棵树。

输出格式
输出一个整数，表示最大价值。

数据范围
1≤N,V≤100
1≤vi,wi≤100

父节点编号范围：
—内部结点：1≤pi≤N;
—根节点 pi=−1;

输出：
11

#include <cmath>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 110;
int n, m;                       //n为物品数量，m为总体积
int v[N], w[N], f[N][N];        //v[i]第i个物品的体积，w[i]第i个物品的价值
int h[N], e[N], ne[N], idx;     //邻接表

void add(int a, int b) {    //邻接表，链表模拟
    e[idx] = b; ne[idx] = h[a]; h[a] = idx++;
}

void dfs(int u) {
    for (int i = h[u]; i != -1; i = ne[i]) {    //循环物品组，遍历树，拿到当前节点u下所有的子节点son
        int son = e[i];
        dfs(son);   //先将以son做为根节点的所有状态求出

        for (int j = m-v[u]; j>=0; j--) {       //循环体积，由于考虑son时，u必须被选取，所以要留出u的体积来
            for (int k = 0; k<=j; k++) {        //循环决策，将体积"0~j"视作物品组，来进行选取
                //f[u][j-k]的含义为以u为根节点，体积为j-k时的最大价值，
                //f[son][k]的含义为以son为根节点，体积为k时的最大价值。
                f[u][j] = max(f[u][j], f[u][j-k] + f[son][k]);
            }
        }
    }
    for (int i = m; i>=v[u]; i--) f[u][i] = f[u][i-v[u]] + w[u];    //将u的价值加到能容下u的方案中，因为上面计算子节点的时候已经给u留过位置了，所以可以直接加
    for (int i = 0; i<v[u]; i++) f[u][i] = 0;                    //所有不能容下u的方案，价值都应该为0，因为不选u代表不选u的所有子节点，那就没有价值
}

int main() {
    //读入，用邻接表存储树
    cin >> n >> m;
    int root, p;
    memset(h, -1, sizeof h);        //邻接表初始化
    for (int i = 1; i<=n; i++) {
        cin >> v[i] >> w[i] >> p;
        if (p == -1) root = i;      //如果p为-1，就是根节点
        else add(p, i);       //不是-1，就是子节点，通过邻接表的方式将点i接在父节点p后面
    }

    dfs(root);

    cout << f[root][m];     //输出以root为根节点并且体积为m时的最大价值
    return 0;
}

思路：
在"背包模型—金明的预算方案"的基础上，本题增加了”子节点的数量“以及”子节点有可能是其他点的父节点“，二进制枚举就不能使用了，因为2^k肯定会超时，所以我们以体积来划分每组背包，还是经典y式dp法。

1.状态表示：
f[i][j]：以i为根节点并且选择i节点时，体积不超过j的所有方案，
属性为Max(最大价值)。

2.状态计算:
还是以 ”选择节点i/不选节点i“ 来做状态转移，

1.不选择节点i的话：那么以i为根节点且体积不超过j的方案的最大价值必然为0，因为不选节点i的话，所有以i为根节点的物品也无法被选择，所以为0。

2.选择节点i的话：
以体积来划分每组背包，
首先i是必选的，所以只需要考虑j-v[i]时的所有体积即可，
f[i][j] = max(i的所有子节点共用体积j-v[i]的所有方案) + w[i]

如果有所帮助请给个免费的赞吧~有人看才是支撑我写下去的动力！

声明：
算法思路来源为y总，详细请见https://www.acwing.com/
本文仅用作学习记录和交流

C++---背包模型---有依赖的背包问题（每日一道算法2023.3.24）

悦读