经过半年呕心沥血的努力,SciSharp STACK终于把Tensorflow .NET绑定升级到可以使用 tensorflow 2.3, 新版本最大的优势是实现了Eager模式, 这个特性是让.NET C#/ F#成为机器学习模型开发工具的重要前置条件。
NugGet包下载:
https://www.nuget.org/packages/TensorFlow.NET/0.20.0 。
欢迎大家入坑体验新版本,提供反馈。
同时作为一个最受欢迎的华人工程师主导开发的.NET机器学习项目,当然要最照顾国内的开发者,所以提供了最详尽的中文开发者文档:
https://github.com/SciSharp/TensorFlow.NET-Tutorials 。
和最实用的完整代码示例:
https://github.com/SciSharp/SciSharp-Stack-Examples 。
微软ML.NET项目组表示会同步跟进:
https://github.com/dotnet/machinelearning/issues/5401。
如果你喜欢我们的项目,请记得收藏和点赞一下哦:
https://github.com/SciSharp/TensorFlow.NET 。
如果有同学对tensorflow运行在龙芯上的事情感兴趣的话,可以一起推进这个事情。
我们目前对龙芯.net还不太了解,希望通过tensorflow .net的移植来加深对龙芯的了解。
为什么说 C# 开发更高效?
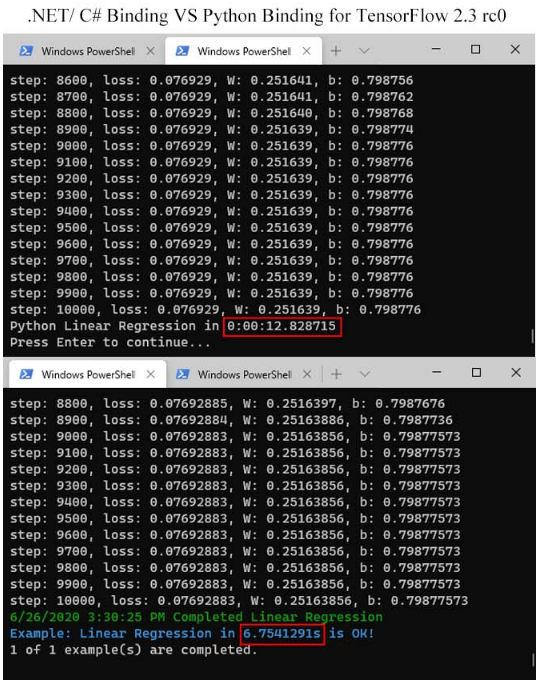
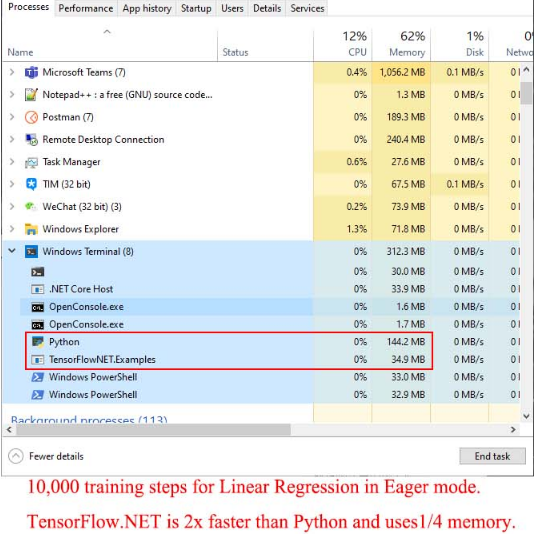
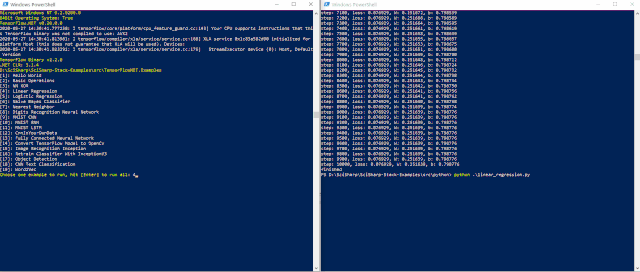
我们通过一个相同数据集的1000轮的线性回归的例子的运行,我们对比 C# 和 Python 的运行速度和内存占用,发现 C# 的速度大约是 Python 的2倍,而内存的使用,C# 只占到 Python 的1/4 ,可以说 TensorFlow 的 C# 版本在速度和性能上同时超过了 Python 版本,因此,在工业现场或者实际应用时,TensorFlow.NET 除了部署上的便利,更有性能上的杰出优势。
下述2个图是具体的对比运行示意图:
我用 C# 写 DNN 案例分享
-- 基于 TensorFlow.NET 2.3 开发
(文章较长,干货较多,读者也可以直接访问GitHub)
1. 深度神经网络(DNN)介绍
2006年, 深度学习鼻祖Hinton在《SCIENCE 》上发表了一篇论文” Reducing the Dimensionality of Data with Neural Networks “,这篇论文揭开了深度学习的序幕。这篇论文提出了两个主要观点:(1)、多层人工神经网络模型有很强的特征学习能力,深度学习模型学习得到的特征数据对原数据有更本质的代表性,这将大大便于分类和可视化问题;(2)、对于深度神经网络很难训练达到最优的问题,可以采用逐层训练方法解决,将上层训练好的结果作为下层训练过程中的初始化参数。
深度神经网络(Deep Neural Networks,简称DNN)是深度学习的基础,想要学好深度学习,首先我们要理解DNN模型。
DNN模型结构:
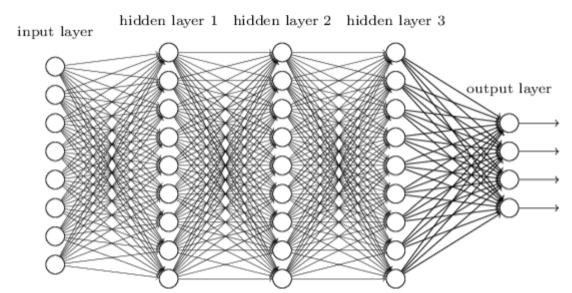
深度神经网络(Deep Neural Networks,DNN)可以理解为有很多隐藏层的神经网络,又被称为深度前馈网络(DFN),多层感知机(Multi-Layer Perceptron,MLP),其具有多层的网络结构,如下图所示:
DNN模型按照层的位置不同,可以分为3种神经网络层:输入层、隐藏层和输出层。一般来说,第一层为输入层,最后一层为输出层,中间为单个或多个隐藏层(某些模型的结构可能不同)。
层与层之间是全连接的,也就是说,第i层的任意一个神经元一定与第i+1层的任意一个神经元相连。虽然DNN看起来很复杂,但是从小的局部结构来看,它还是和普通的感知机一样,即一个线性函数搭配一个激活函数。
DNN前向传播:
利用若干个权重系数矩阵W,偏置向量 b 来和输入向量 X 进行一系列线性运算和激活运算,从输入层开始,一层层地向后计算,一直到运算到输出层,得到输出结果的值。
DNN反向传播:
深度学习的过程即找到网络各层中最优的线性系数矩阵 W 和偏置向量 b,让所有的输入样本通过网络计算后,预测的输出尽可能等于或者接近实际的输出样本,这样的过程一般称为反向传播。
我们需要定义一个损失函数,来衡量预测输出值和实际输出值之间的差异。接着对这个损失函数进行优化,通过不断迭代对线性系数矩阵 W 和 偏置向量 b 进行更新,让损失函数最小化,不断逼近最小极值 或 满足我们预期的需求。在DNN中, 损失函数优化极值求解的过程最常见的一般是通过梯度下降法来一步步迭代完成的。
DNN在TensorFlow2.0中的一般流程:
Step - 1:数据加载、归一化和预处理;
Step - 2:搭建深度神经网络模型;
Step - 3:定义损失函数和准确率函数;
Step - 4:模型训练;
Step - 5:模型预测推理,性能评估。
DNN中的过拟合:
随着网络的层数加深,模型的训练过程中会出现 梯度爆炸、梯度消失、欠拟合和过拟合,我们来说说比较常见的过拟合。过拟合一般是指模型的特征维度过多、参数过多,模型过于复杂,导致参数数量大大高于训练数据,训练出的网络层过于完美地适配训练集,但对新的未知的数据集的预测能力很差。即过度地拟合了训练数据,而没有考虑到模型的泛化能力。
一般的解决方法:
获取更多数据:从数据源获得更多数据,或做数据增强;
数据预处理:清洗数据、减少特征维度、类别平衡;
正则化:限制权重过大、网络层数过多,避免模型过于复杂;
多种模型结合:集成学习的思想;
Dropout:随机从网络中去掉一部分隐藏神经元;
中止方法:限制训练时间、次数,及早停止。
接下来,我们通过2种 TensorFlow2.x 推荐的方式 Eager 和 Keras 的代码来演示 DNN 下的 MNIST 训练集的训练和推理,其中的线性函数和交叉熵损失函数等细节说明,请读者参考“6. MNIST手写字符分类 Logistic Regression”一章节,这里不再赘述。
2. TensorFlow.NET 代码实操 1 - DNN with Eager
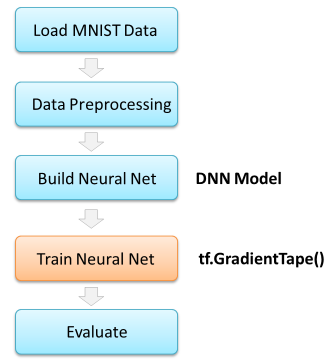
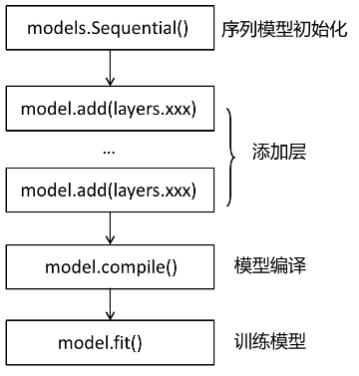
Eager 模式下的 DNN 模型训练流程简述如下:
按照上述流程,我们进入代码实操阶段。
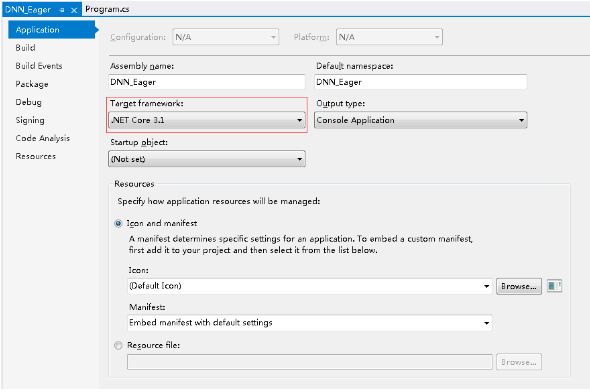
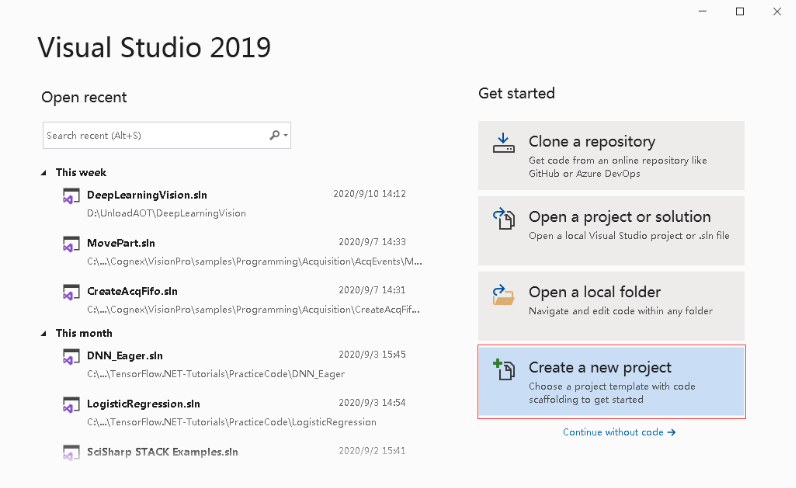
① 新建项目,配置环境和引用:
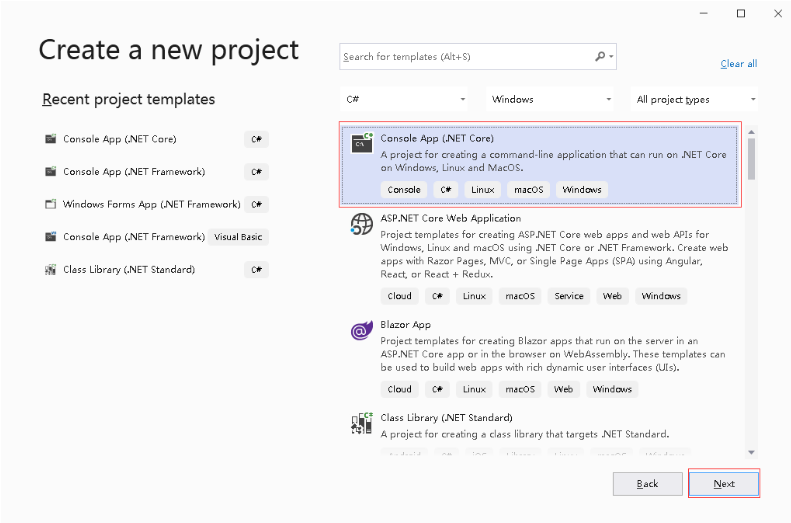
新建项目。
选择 .NET Core 框架。
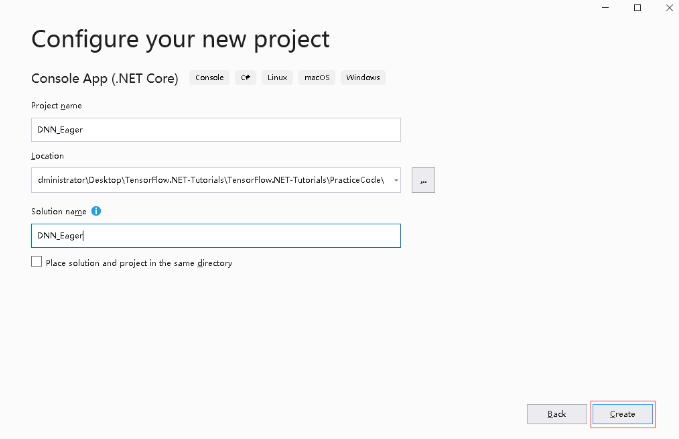
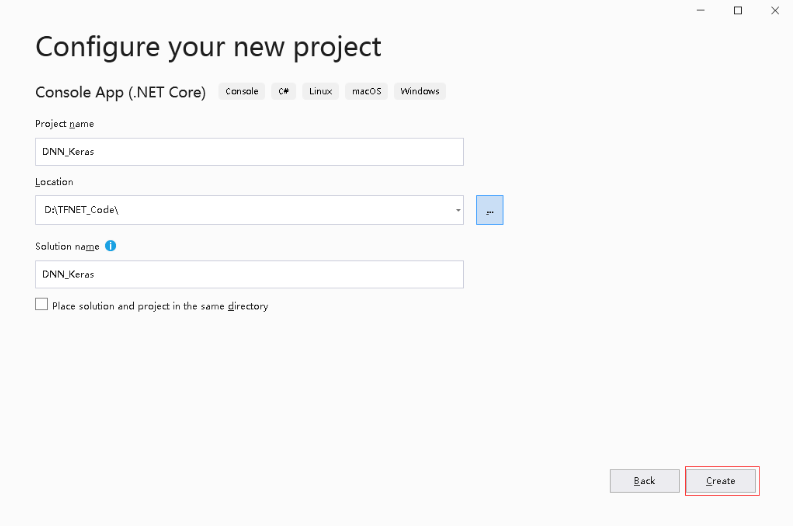
输入项目名,DNN_Eager。
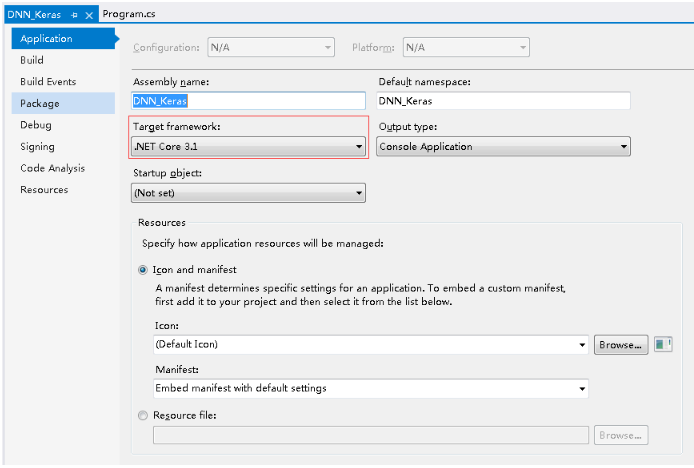
确认 .NET Core 版本为 3.0 及以上。
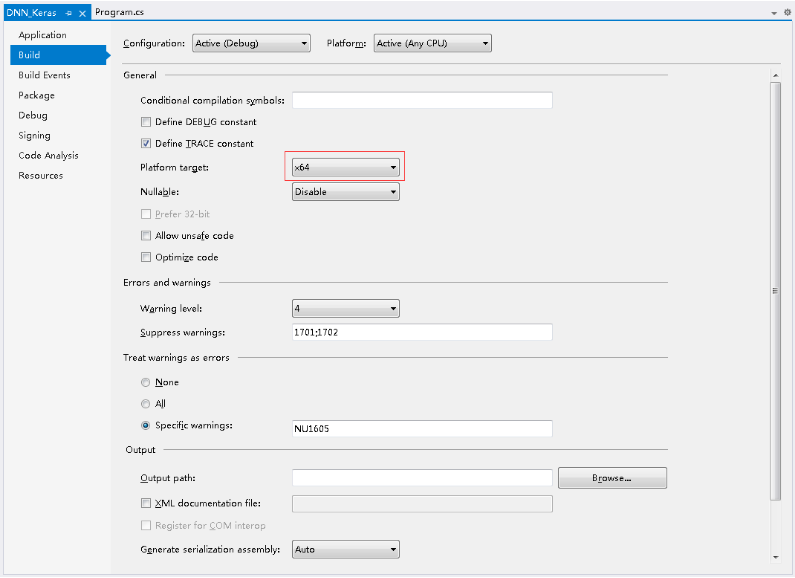
选择目标平台为 x64 。
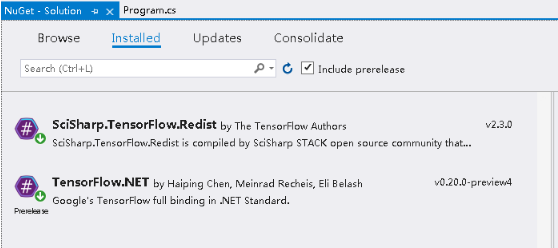
使用 NuGet 安装 TensorFlow.NET 和 SciSharp.TensorFlow.Redist,如果需要使用 GPU,则安装 SciSharp.TensorFlow.Redist-Windows-GPU。
添加项目引用。
using NumSharp;
using System.Linq;
using Tensorflow;
using Tensorflow.Keras.Optimizers;
using static Tensorflow.Binding;② 定义网络权重变量和超参数:
int num_classes = 10; // MNIST 的字符类别 0~9 总共 10 类
int num_features = 784; // 输入图像的特征尺寸,即像素28*28=784
// 超参数
float learning_rate = 0.001f;// 学习率
int training_steps = 1000;// 训练轮数
int batch_size = 256;// 批次大小
int display_step = 100;// 训练数据 显示周期
// 神经网络参数
int n_hidden_1 = 128; // 第1层隐藏层的神经元数量
int n_hidden_2 = 256; // 第2层隐藏层的神经元数量
IDatasetV2 train_data;// MNIST 数据集
NDArray x_test, y_test, x_train, y_train;// 数据集拆分为训练集和测试集
IVariableV1 h1, h2, wout, b1, b2, bout;// 待训练的权重变量
float accuracy_test = 0f;// 测试集准确率③ 载入MNIST数据,并进行预处理:
数据下载 或 从本地加载 → 数据展平 → 归一化 → 转换 Dataset → 无限复制(方便后面take) / 乱序 / 生成批次 / 预加载 → 预处理后的数据提取需要的训练份数。
((x_train, y_train), (x_test, y_test)) = tf.keras.datasets.mnist.load_data();// 下载 或 加载本地 MNIST
(x_train, x_test) = (x_train.reshape((-1, num_features)), x_test.reshape((-1, num_features)));// 输入数据展平
(x_train, x_test) = (x_train / 255f, x_test / 255f);// 归一化
train_data = tf.data.Dataset.from_tensor_slices(x_train, y_train);//转换为 Dataset 格式
train_data = train_data.repeat()
.shuffle(5000)
.batch(batch_size)
.prefetch(1)
.take(training_steps);// 数据预处理④ 初始化网络权重变量和优化器:
随机初始化网络权重变量,并打包成数组方便后续梯度求导作为参数。
// 随机初始化网络权重变量,并打包成数组方便后续梯度求导作为参数。
var random_normal = tf.initializers.random_normal_initializer();
h1 = tf.Variable(random_normal.Apply(new InitializerArgs((num_features, n_hidden_1))));
h2 = tf.Variable(random_normal.Apply(new InitializerArgs((n_hidden_1, n_hidden_2))));
wout = tf.Variable(random_normal.Apply(new InitializerArgs((n_hidden_2, num_classes))));
b1 = tf.Variable(tf.zeros(n_hidden_1));
b2 = tf.Variable(tf.zeros(n_hidden_2));
bout = tf.Variable(tf.zeros(num_classes));
var trainable_variables = new IVariableV1[] { h1, h2, wout, b1, b2, bout };采用随机梯度下降优化器。
// 采用随机梯度下降优化器
var optimizer = tf.optimizers.SGD(learning_rate);⑤ 搭建DNN网络模型,训练并周期显示训练过程:
搭建4层的全连接神经网络,隐藏层采用 sigmoid 激活函数,输出层采用 softmax 输出预测的概率分布。
// 搭建网络模型
Tensor neural_net(Tensor x)
{
// 第1层隐藏层采用128个神经元。
var layer_1 = tf.add(tf.matmul(x, h1.AsTensor()), b1.AsTensor());
// 使用 sigmoid 激活函数,增加层输出的非线性特征
layer_1 = tf.nn.sigmoid(layer_1);
// 第2层隐藏层采用256个神经元。
var layer_2 = tf.add(tf.matmul(layer_1, h2.AsTensor()), b2.AsTensor());
// 使用 sigmoid 激活函数,增加层输出的非线性特征
layer_2 = tf.nn.sigmoid(layer_2);
// 输出层的神经元数量和标签类型数量相同
var out_layer = tf.matmul(layer_2, wout.AsTensor()) + bout.AsTensor();
// 使用 Softmax 函数将输出类别转换为各类别的概率分布
return tf.nn.softmax(out_layer);
}创建交叉熵损失函数。
// 交叉熵损失函数
Tensor cross_entropy(Tensor y_pred, Tensor y_true)
{
// 将标签转换为One-Hot格式
y_true = tf.one_hot(y_true, depth: num_classes);
// 保持预测值在 1e-9 和 1.0 之间,防止值下溢出现log(0)报错
y_pred = tf.clip_by_value(y_pred, 1e-9f, 1.0f);
// 计算交叉熵损失
return tf.reduce_mean(-tf.reduce_sum(y_true * tf.math.log(y_pred)));
}应用 TensorFlow 2.x 中的自动求导机制,创建梯度记录器,自动跟踪网络中的梯度,自动求导进行梯度下降和网络权重变量的更新优化。每隔一定周期,打印出当前轮次网络的训练性能数据 loss 和 accuracy 。关于自动求导机制,请参考“6. MNIST手写字符分类 Logistic Regression”一章节。
// 运行优化器
void run_optimization(OptimizerV2 optimizer, Tensor x, Tensor y, IVariableV1[] trainable_variables)
{
using var g = tf.GradientTape();
var pred = neural_net(x);
var loss = cross_entropy(pred, y);
// 计算梯度
var gradients = g.gradient(loss, trainable_variables);
// 更新模型权重 w 和 b
var a = zip(gradients, trainable_variables.Select(x => x as ResourceVariable));
optimizer.apply_gradients(zip(gradients, trainable_variables.Select(x => x as ResourceVariable)));
}// 模型预测准确度
Tensor accuracy(Tensor y_pred, Tensor y_true)
{
// 使用 argmax 提取预测概率最大的标签,和实际值比较,计算模型预测的准确度
var correct_prediction = tf.equal(tf.argmax(y_pred, 1), tf.cast(y_true, tf.int64));
return tf.reduce_mean(tf.cast(correct_prediction, tf.float32), axis: -1);
}// 训练模型
foreach (var (step, (batch_x, batch_y)) in enumerate(train_data, 1))
{
// 运行优化器 进行模型权重 w 和 b 的更新
run_optimization(optimizer, batch_x, batch_y, trainable_variables);
if (step % display_step == 0)
{
var pred = neural_net(batch_x);
var loss = cross_entropy(pred, batch_y);
var acc = accuracy(pred, batch_y);
print($"step: {step}, loss: {(float)loss}, accuracy: {(float)acc}");
}
}⑥ 测试集上性能评估:
在测试集上对训练后的模型进行预测准确率性能评估。
// 在测试集上对训练后的模型进行预测准确率性能评估
{
var pred = neural_net(x_test);
accuracy_test = (float)accuracy(pred, y_test);
print($"Test Accuracy: {accuracy_test}");
}完整的控制台运行代码如下:
using NumSharp;
using System.Linq;
using Tensorflow;
using Tensorflow.Keras.Optimizers;
using static Tensorflow.Binding;
namespace DNN_Eager
{
class Program
{
static void Main(string[] args)
{
DNN_Eager dnn = new DNN_Eager();
dnn.Main();
}
}
class DNN_Eager
{
int num_classes = 10; // MNIST 的字符类别 0~9 总共 10 类
int num_features = 784; // 输入图像的特征尺寸,即像素28*28=784
// 超参数
float learning_rate = 0.001f;// 学习率
int training_steps = 1000;// 训练轮数
int batch_size = 256;// 批次大小
int display_step = 100;// 训练数据 显示周期
// 神经网络参数
int n_hidden_1 = 128; // 第1层隐藏层的神经元数量
int n_hidden_2 = 256; // 第2层隐藏层的神经元数量
IDatasetV2 train_data;// MNIST 数据集
NDArray x_test, y_test, x_train, y_train;// 数据集拆分为训练集和测试集
IVariableV1 h1, h2, wout, b1, b2, bout;// 待训练的权重变量
float accuracy_test = 0f;// 测试集准确率
public void Main()
{
((x_train, y_train), (x_test, y_test)) = tf.keras.datasets.mnist.load_data();// 下载 或 加载本地 MNIST
(x_train, x_test) = (x_train.reshape((-1, num_features)), x_test.reshape((-1, num_features)));// 输入数据展平
(x_train, x_test) = (x_train / 255f, x_test / 255f);// 归一化
train_data = tf.data.Dataset.from_tensor_slices(x_train, y_train);//转换为 Dataset 格式
train_data = train_data.repeat()
.shuffle(5000)
.batch(batch_size)
.prefetch(1)
.take(training_steps);// 数据预处理
// 随机初始化网络权重变量,并打包成数组方便后续梯度求导作为参数。
var random_normal = tf.initializers.random_normal_initializer();
h1 = tf.Variable(random_normal.Apply(new InitializerArgs((num_features, n_hidden_1))));
h2 = tf.Variable(random_normal.Apply(new InitializerArgs((n_hidden_1, n_hidden_2))));
wout = tf.Variable(random_normal.Apply(new InitializerArgs((n_hidden_2, num_classes))));
b1 = tf.Variable(tf.zeros(n_hidden_1));
b2 = tf.Variable(tf.zeros(n_hidden_2));
bout = tf.Variable(tf.zeros(num_classes));
var trainable_variables = new IVariableV1[] { h1, h2, wout, b1, b2, bout };
// 采用随机梯度下降优化器
var optimizer = tf.optimizers.SGD(learning_rate);
// 训练模型
foreach (var (step, (batch_x, batch_y)) in enumerate(train_data, 1))
{
// 运行优化器 进行模型权重 w 和 b 的更新
run_optimization(optimizer, batch_x, batch_y, trainable_variables);
if (step % display_step == 0)
{
var pred = neural_net(batch_x);
var loss = cross_entropy(pred, batch_y);
var acc = accuracy(pred, batch_y);
print($"step: {step}, loss: {(float)loss}, accuracy: {(float)acc}");
}
}
// 在测试集上对训练后的模型进行预测准确率性能评估
{
var pred = neural_net(x_test);
accuracy_test = (float)accuracy(pred, y_test);
print($"Test Accuracy: {accuracy_test}");
}
}
// 运行优化器
void run_optimization(OptimizerV2 optimizer, Tensor x, Tensor y, IVariableV1[] trainable_variables)
{
using var g = tf.GradientTape();
var pred = neural_net(x);
var loss = cross_entropy(pred, y);
// 计算梯度
var gradients = g.gradient(loss, trainable_variables);
// 更新模型权重 w 和 b
var a = zip(gradients, trainable_variables.Select(x => x as ResourceVariable));
optimizer.apply_gradients(zip(gradients, trainable_variables.Select(x => x as ResourceVariable)));
}
// 模型预测准确度
Tensor accuracy(Tensor y_pred, Tensor y_true)
{
// 使用 argmax 提取预测概率最大的标签,和实际值比较,计算模型预测的准确度
var correct_prediction = tf.equal(tf.argmax(y_pred, 1), tf.cast(y_true, tf.int64));
return tf.reduce_mean(tf.cast(correct_prediction, tf.float32), axis: -1);
}
// 搭建网络模型
Tensor neural_net(Tensor x)
{
// 第1层隐藏层采用128个神经元。
var layer_1 = tf.add(tf.matmul(x, h1.AsTensor()), b1.AsTensor());
// 使用 sigmoid 激活函数,增加层输出的非线性特征
layer_1 = tf.nn.sigmoid(layer_1);
// 第2层隐藏层采用256个神经元。
var layer_2 = tf.add(tf.matmul(layer_1, h2.AsTensor()), b2.AsTensor());
// 使用 sigmoid 激活函数,增加层输出的非线性特征
layer_2 = tf.nn.sigmoid(layer_2);
// 输出层的神经元数量和标签类型数量相同
var out_layer = tf.matmul(layer_2, wout.AsTensor()) + bout.AsTensor();
// 使用 Softmax 函数将输出类别转换为各类别的概率分布
return tf.nn.softmax(out_layer);
}
// 交叉熵损失函数
Tensor cross_entropy(Tensor y_pred, Tensor y_true)
{
// 将标签转换为One-Hot格式
y_true = tf.one_hot(y_true, depth: num_classes);
// 保持预测值在 1e-9 和 1.0 之间,防止值下溢出现log(0)报错
y_pred = tf.clip_by_value(y_pred, 1e-9f, 1.0f);
// 计算交叉熵损失
return tf.reduce_mean(-tf.reduce_sum(y_true * tf.math.log(y_pred)));
}
}
}
运行结果如下:
step: 100, loss: 562.84094, accuracy: 0.2734375
step: 200, loss: 409.87466, accuracy: 0.51171875
step: 300, loss: 234.70618, accuracy: 0.70703125
step: 400, loss: 171.07526, accuracy: 0.8046875
step: 500, loss: 147.40372, accuracy: 0.86328125
step: 600, loss: 123.477295, accuracy: 0.8671875
step: 700, loss: 105.51019, accuracy: 0.8984375
step: 800, loss: 106.7933, accuracy: 0.87109375
step: 900, loss: 75.033554, accuracy: 0.921875
Test Accuracy: 0.8954我们可以看到,loss 在不断地下降,accuracy 不断提高,最终的测试集的准确率为 0.8954,略低于 训练集上的准确率 0.9219,基本属于一个比较合理的训练结果。
3. TensorFlow.NET Keras 模型构建的三种方式
TensorFlow.NET 2.x 提供了3种定义 Keras 模型的方式:
Sequential API (序列模型):按层顺序创建模型
Functional API (函数式模型):函数式API创建任意结构模型
Model Subclassing (自定义模型):Model子类化创建自定义模型
推荐的使用优先级:
优先使用 Sequential API 进行模型的快速搭建,如果无法满足需求(共享层或多输入等),再考虑采用 Functional API 创建自定义结构的模型,如果仍然无法满足需求(需要自定义控制 Train 过程或研发创新想法),最后也可以考虑 Model Subclassing。
针对各种场景,TensorFlow.NET 都提供了对应的快速解决方案,接下来我们来详细说明下这3种模型搭建的方式。
3.1 Sequential API (序列模型)
这是 Keras 最简单的构建模型方式(也许是所有框架中最简单构建方式),它顺序地把所有模型层依次定义,然后使用内置的训练循环 model.fit 对模型进行训练, 搭建模型和训练的过程就像“搭建乐高积木”一样简单。
但序列模型是 layer-by-layer 的,某些场景的使用略有限制:
无法共享网络层
不能创建多分支结构
不能有多个输入
这种方式特别适用于经典网络模型,如:LeNet,AlexNet,VGGNet ,模型结构如图所示:
Sequential 方式一般的代码流程如下:
//TODO: TensorFlow.NET的代码示例待完成后添加
3.2 Functional API (函数式模型)
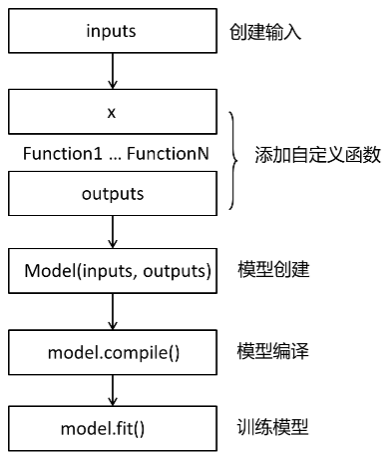
简单的 Sequential 堆叠方式有时候不能表示任意结构的神经网络。为此, Keras 提供了 Functional API, 帮助我们建立更为复杂和灵活的模型,它可以处理非线性拓扑、具有共享层的模型和具有多个输入或输出的模型。其使用方法是将层作为可调用的对象并返回张量,并将输入向量和输出向量提供给 Model 的 inputs 和 outputs 参数。
Functional API 有如下更强的功能:
定义更复杂的模型
支持多输入多输出
可以定义模型分支,比如inception block , resnet block
方便layer共享
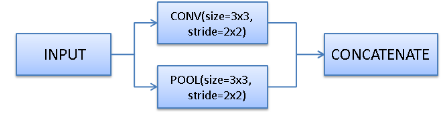
实际上,任意的 Sequential 模型 都可以使用 Functional 方式实现,Functional 方式特别适用于一些复杂的网络模型,如:ResNet,GoogleNet/Inception,Xception,SqueezeNet 等,模型结构如图所示:
Functional 方式一般的代码流程如下:
//TODO: TensorFlow.NET的代码示例待完成后添加
3.3 Model Subclassing (自定义模型)
Functional API 通过继承 Model 来编写自己的模型类,如果仍然无法满足需求,则可以通过 Model 子类化创建自定义模型,主要为自定义层(可以继承 Layer 类)、自定义损失函数(可以继承 Loss 类)和自定义评价函数(可以继承 Metric 类)。
从开发人员的角度来看,这种工作方式是扩展框架定义的模型类,实例化层,然后编写模型的正向传递。TensorFlow.NET 2.x通过 Keras Subclassing API 支持这种开箱即用的方式,在 Keras 中 Model 类作为基本的类,可以在此基础上,进行任意的自定义操作,对模型的所有部分(包括训练过程)进行控制。
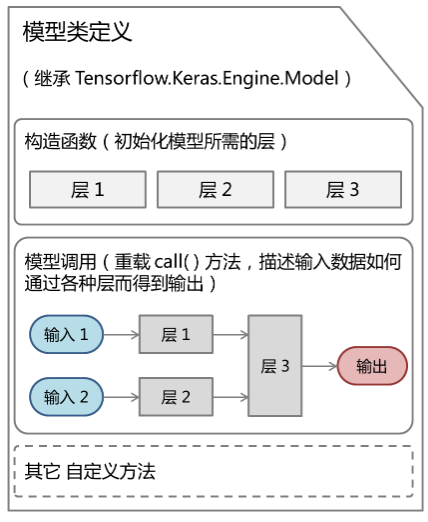
我们先来了解下 Keras 模型类的自定义示意图:
然后,我们通过示例代码来了解 Model Subclassing 方式的具体流程。
自定义模型需要继承 Tensorflow.Keras.Engine.Model 类,然后在构造函数中初始化所需要的层(可以使用 keras 的层或者继承 Layer 进行自定义层),并重载 call() 方法进行模型的调用,建立输入和输出之间的函数关系。
代码结构如下:
public class MyModel : Model
{
Layer myLayer1;
Layer myLayer2;
Layer output;
public MyModel(ModelArgs args) :
base(args)
{
// First layer.
myLayer1 = Layer.xxx;
// Second layer.
myLayer2 = Layer.xxx;
output = Layer.xxx;
}
// Set forward pass.
protected override Tensor call(Tensor inputs)
{
inputs = myLayer1.Apply(inputs);
inputs = myLayer2.Apply(inputs);
inputs = output.Apply(inputs);
return inputs;
}
}以上的代码说明了自定义模型的方法,类似地也可以自定义层、损失函数和评估函数。
ps:实际上,通过Mode Subclassing 方式自定义的模型,也可以使用 Sequential 或者 Functional API,其中自定义的 Layer 需要添加 get_config 方法以序列化组合模型。
4. TensorFlow.NET 代码实操 2 - DNN with Keras
Keras 方式的 DNN 实现流程和上述第2节中的 Eager 方式类似,差异部分主要是使用了 Keras 的全连接层(Dense)替代了 Eager 方式中的 “线性变换+激活函数”。
TensorFlow.NET 2.x 主要推荐使用 Keras 进行模型搭建和训练,Keras 是一个高级神经网络 API,可以实现简单、快速和灵活地搭建网络模型。自从2017年 TensorFlow 1.2 开始,Keras 就从一个独立运行后端,变为 TensorFlow 的核心内置 API,一直到 TensorFlow 2.0 发布后,Keras 由 TensorFlow 官方推荐给广大开发者,替代 TF-Slim 作为官方默认的深度学习开发的首选框架。
Keras 有2个比较重要的概念:模型(Model)和层(Layer)。层(Layer)将常用的神经网络层进行了封装(全连接层、卷积层、池化层等),模型(Model)将各个层进行连接,并封装成一个完整的网络模型。模型调用的时候,使用 y_pred = model (x) 的形式即可。
Keras 在 Tensorflow.Keras.Engine.Layer 下内置了深度学习中常用的网络层,同时也支持继承并自定义层。
模型(Model)作为类的方式构造,通过继承 Tensorflow.Keras.Engine.Model 这个类在定义自己的模型。在继承类中,我们需要重写该类的构造函数进行初始化(初始化模型需要的层和组织结构),并通过重载 call( ) 方法来进行模型的调用,同时支持增加自定义方法。
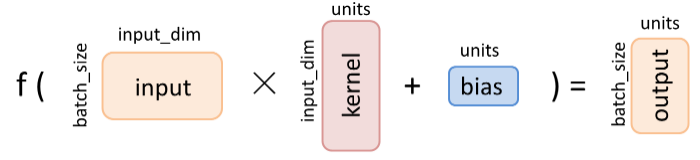
本次 DNN 案例中,我们主要使用 Keras 中的全连接层。全连接层(Fully-connected Layer,Tensorflow.Keras.Engine.Layer.Dense)是 Keras 中最基础和常用的层之一,对输入矩阵 x 进行 f ( x w + b)的线性变换 + 激活函数操作。Dense 层的函数如下图所示:
Dense 层主要有下述2个参数:
参数1:units,int 类型,输出张量的维度;int units, Activation activation;
参数2:activation,Tensorflow.Keras.Activation 类型,激活函数(常用的激活函数有 Linear,Relu,Sigmoid,Tanh)。
接下来我们通过代码来逐步实操 Keras 下的 DNN 。
① 新建项目,配置环境和引用:
新建项目。
选择 .NET Core 框架。
输入项目名,DNN_Keras。
确认 .NET Core 版本为 3.0 及以上。
选择目标平台为 x64 。
使用 NuGet 安装 TensorFlow.NET 和 SciSharp.TensorFlow.Redist,如果需要使用 GPU,则安装 SciSharp.TensorFlow.Redist-Windows-GPU。
添加项目引用。
using NumSharp;
using System;
using System.Linq;
using Tensorflow;
using Tensorflow.Keras;
using Tensorflow.Keras.ArgsDefinition;
using Tensorflow.Keras.Engine;
using static Tensorflow.Binding;② 定义网络层参数、训练数据和超参数:
int num_classes = 10; // 0 to 9 digits
int num_features = 784; // 28*28 image size
// Training parameters.
float learning_rate = 0.1f;
int display_step = 100;
int batch_size = 256;
int training_steps = 1000;
// Train Variables
float accuracy;
IDatasetV2 train_data;
NDArray x_test, y_test, x_train, y_train;③ 载入MNIST数据,并进行预处理:
数据下载 或 从本地加载 → 数据展平 → 归一化 → 转换 Dataset → 无限复制(方便后面take) / 乱序 / 生成批次 / 预加载 → 预处理后的数据提取需要的训练份数。
// Prepare MNIST data.
((x_train, y_train), (x_test, y_test)) = tf.keras.datasets.mnist.load_data();
// Flatten images to 1-D vector of 784 features (28*28).
(x_train, x_test) = (x_train.reshape((-1, num_features)), x_test.reshape((-1, num_features)));
// Normalize images value from [0, 255] to [0, 1].
(x_train, x_test) = (x_train / 255f, x_test / 255f);
// Use tf.data API to shuffle and batch data.
train_data = tf.data.Dataset.from_tensor_slices(x_train, y_train);
train_data = train_data.repeat()
.shuffle(5000)
.batch(batch_size)
.prefetch(1)
.take(training_steps);④ 搭建 Keras 网络模型:
Model Subclassing 方式搭建 Keras 的 DNN 网络模型,输入层参数。
// Build neural network model.
var neural_net = new NeuralNet(new NeuralNetArgs
{
NumClasses = num_classes,
NeuronOfHidden1 = 128,
Activation1 = tf.keras.activations.Relu,
NeuronOfHidden2 = 256,
Activation2 = tf.keras.activations.Relu
});继承 Model 类,搭建全连接神经网络 Dense Neural Net。在构造函数中创建网络的层结构,并重载 call( ) 方法,指定输入和输出之间的函数关系。
// Model Subclassing
public class NeuralNet : Model
{
Layer fc1;
Layer fc2;
Layer output;
public NeuralNet(NeuralNetArgs args) :
base(args)
{
// First fully-connected hidden layer.
fc1 = Dense(args.NeuronOfHidden1, activation: args.Activation1);
// Second fully-connected hidden layer.
fc2 = Dense(args.NeuronOfHidden2, activation: args.Activation2);
output = Dense(args.NumClasses);
}
// Set forward pass.
protected override Tensor call(Tensor inputs, bool is_training = false, Tensor state = null)
{
inputs = fc1.Apply(inputs);
inputs = fc2.Apply(inputs);
inputs = output.Apply(inputs);
if (!is_training)
inputs = tf.nn.softmax(inputs);
return inputs;
}
}
// Network parameters.
public class NeuralNetArgs : ModelArgs
{
/// <summary>
/// 1st layer number of neurons.
/// </summary>
public int NeuronOfHidden1 { get; set; }
public Activation Activation1 { get; set; }
/// <summary>
/// 2nd layer number of neurons.
/// </summary>
public int NeuronOfHidden2 { get; set; }
public Activation Activation2 { get; set; }
public int NumClasses { get; set; }
}⑤ 训练模型并周期显示训练过程:
交叉熵损失函数和准确率评估函数。
// Cross-Entropy Loss.
Func<Tensor, Tensor, Tensor> cross_entropy_loss = (x, y) =>
{
// Convert labels to int 64 for tf cross-entropy function.
y = tf.cast(y, tf.int64);
// Apply softmax to logits and compute cross-entropy.
var loss = tf.nn.sparse_softmax_cross_entropy_with_logits(labels: y, logits: x);
// Average loss across the batch.
return tf.reduce_mean(loss);
};
// Accuracy metric.
Func<Tensor, Tensor, Tensor> accuracy = (y_pred, y_true) =>
{
// Predicted class is the index of highest score in prediction vector (i.e. argmax).
var correct_prediction = tf.equal(tf.argmax(y_pred, 1), tf.cast(y_true, tf.int64));
return tf.reduce_mean(tf.cast(correct_prediction, tf.float32), axis: -1);
};创建随机梯度下降(SDG)优化器和执行方法。
// Stochastic gradient descent optimizer.
var optimizer = tf.optimizers.SGD(learning_rate);
// Optimization process.
Action<Tensor, Tensor> run_optimization = (x, y) =>
{
// Wrap computation inside a GradientTape for automatic differentiation.
using var g = tf.GradientTape();
// Forward pass.
var pred = neural_net.Apply(x, is_training: true);
var loss = cross_entropy_loss(pred, y);
// Compute gradients.
var gradients = g.gradient(loss, neural_net.trainable_variables);
// Update W and b following gradients.
optimizer.apply_gradients(zip(gradients, neural_net.trainable_variables.Select(x => x as ResourceVariable)));
};应用 TensorFlow 2.x 中的自动求导机制,自动求导进行梯度下降和网络权重变量的更新优化。每隔一定周期,打印出当前轮次网络的训练性能数据 loss 和 accuracy 。关于自动求导机制,请参考“6. MNIST手写字符分类 Logistic Regression”一章节。
// Run training for the given number of steps.
foreach (var (step, (batch_x, batch_y)) in enumerate(train_data, 1))
{
// Run the optimization to update W and b values.
run_optimization(batch_x, batch_y);
if (step % display_step == 0)
{
var pred = neural_net.Apply(batch_x, is_training: true);
var loss = cross_entropy_loss(pred, batch_y);
var acc = accuracy(pred, batch_y);
print($"step: {step}, loss: {(float)loss}, accuracy: {(float)acc}");
}
}⑥ 测试集上性能评估:
在测试集上对训练后的模型进行预测准确率性能评估。
// Test model on validation set.
{
var pred = neural_net.Apply(x_test, is_training: false);
this.accuracy = (float)accuracy(pred, y_test);
print($"Test Accuracy: {this.accuracy}");
}完整的控制台运行代码如下:
using NumSharp;
using System;
using System.Linq;
using Tensorflow;
using Tensorflow.Keras;
using Tensorflow.Keras.ArgsDefinition;
using Tensorflow.Keras.Engine;
using static Tensorflow.Binding;
namespace DNN_Keras
{
class Program
{
static void Main(string[] args)
{
DNN_Keras dnn = new DNN_Keras();
dnn.Main();
}
}
class DNN_Keras
{
int num_classes = 10; // 0 to 9 digits
int num_features = 784; // 28*28 image size
// Training parameters.
float learning_rate = 0.1f;
int display_step = 100;
int batch_size = 256;
int training_steps = 1000;
// Train Variables
float accuracy;
IDatasetV2 train_data;
NDArray x_test, y_test, x_train, y_train;
public void Main()
{
// Prepare MNIST data.
((x_train, y_train), (x_test, y_test)) = tf.keras.datasets.mnist.load_data();
// Flatten images to 1-D vector of 784 features (28*28).
(x_train, x_test) = (x_train.reshape((-1, num_features)), x_test.reshape((-1, num_features)));
// Normalize images value from [0, 255] to [0, 1].
(x_train, x_test) = (x_train / 255f, x_test / 255f);
// Use tf.data API to shuffle and batch data.
train_data = tf.data.Dataset.from_tensor_slices(x_train, y_train);
train_data = train_data.repeat()
.shuffle(5000)
.batch(batch_size)
.prefetch(1)
.take(training_steps);
// Build neural network model.
var neural_net = new NeuralNet(new NeuralNetArgs
{
NumClasses = num_classes,
NeuronOfHidden1 = 128,
Activation1 = tf.keras.activations.Relu,
NeuronOfHidden2 = 256,
Activation2 = tf.keras.activations.Relu
});
// Cross-Entropy Loss.
Func<Tensor, Tensor, Tensor> cross_entropy_loss = (x, y) =>
{
// Convert labels to int 64 for tf cross-entropy function.
y = tf.cast(y, tf.int64);
// Apply softmax to logits and compute cross-entropy.
var loss = tf.nn.sparse_softmax_cross_entropy_with_logits(labels: y, logits: x);
// Average loss across the batch.
return tf.reduce_mean(loss);
};
// Accuracy metric.
Func<Tensor, Tensor, Tensor> accuracy = (y_pred, y_true) =>
{
// Predicted class is the index of highest score in prediction vector (i.e. argmax).
var correct_prediction = tf.equal(tf.argmax(y_pred, 1), tf.cast(y_true, tf.int64));
return tf.reduce_mean(tf.cast(correct_prediction, tf.float32), axis: -1);
};
// Stochastic gradient descent optimizer.
var optimizer = tf.optimizers.SGD(learning_rate);
// Optimization process.
Action<Tensor, Tensor> run_optimization = (x, y) =>
{
// Wrap computation inside a GradientTape for automatic differentiation.
using var g = tf.GradientTape();
// Forward pass.
var pred = neural_net.Apply(x, is_training: true);
var loss = cross_entropy_loss(pred, y);
// Compute gradients.
var gradients = g.gradient(loss, neural_net.trainable_variables);
// Update W and b following gradients.
optimizer.apply_gradients(zip(gradients, neural_net.trainable_variables.Select(x => x as ResourceVariable)));
};
// Run training for the given number of steps.
foreach (var (step, (batch_x, batch_y)) in enumerate(train_data, 1))
{
// Run the optimization to update W and b values.
run_optimization(batch_x, batch_y);
if (step % display_step == 0)
{
var pred = neural_net.Apply(batch_x, is_training: true);
var loss = cross_entropy_loss(pred, batch_y);
var acc = accuracy(pred, batch_y);
print($"step: {step}, loss: {(float)loss}, accuracy: {(float)acc}");
}
}
// Test model on validation set.
{
var pred = neural_net.Apply(x_test, is_training: false);
this.accuracy = (float)accuracy(pred, y_test);
print($"Test Accuracy: {this.accuracy}");
}
}
// Model Subclassing
public class NeuralNet : Model
{
Layer fc1;
Layer fc2;
Layer output;
public NeuralNet(NeuralNetArgs args) :
base(args)
{
// First fully-connected hidden layer.
fc1 = Dense(args.NeuronOfHidden1, activation: args.Activation1);
// Second fully-connected hidden layer.
fc2 = Dense(args.NeuronOfHidden2, activation: args.Activation2);
output = Dense(args.NumClasses);
}
// Set forward pass.
protected override Tensor call(Tensor inputs, bool is_training = false, Tensor state = null)
{
inputs = fc1.Apply(inputs);
inputs = fc2.Apply(inputs);
inputs = output.Apply(inputs);
if (!is_training)
inputs = tf.nn.softmax(inputs);
return inputs;
}
}
// Network parameters.
public class NeuralNetArgs : ModelArgs
{
/// <summary>
/// 1st layer number of neurons.
/// </summary>
public int NeuronOfHidden1 { get; set; }
public Activation Activation1 { get; set; }
/// <summary>
/// 2nd layer number of neurons.
/// </summary>
public int NeuronOfHidden2 { get; set; }
public Activation Activation2 { get; set; }
public int NumClasses { get; set; }
}
}
}
运行结果如下:
The file C:\Users\Administrator\AppData\Local\Temp\mnist.npz already exists
step: 100, loss: 0.4122764, accuracy: 0.9140625
step: 200, loss: 0.28498638, accuracy: 0.921875
step: 300, loss: 0.21436812, accuracy: 0.93359375
step: 400, loss: 0.23279168, accuracy: 0.91796875
step: 500, loss: 0.23876348, accuracy: 0.91015625
step: 600, loss: 0.1752773, accuracy: 0.95703125
step: 700, loss: 0.14060633, accuracy: 0.97265625
step: 800, loss: 0.14577743, accuracy: 0.95703125
step: 900, loss: 0.15461099, accuracy: 0.953125
Test Accuracy: 0.9522我们可以看到,loss 在不断地下降,accuracy 不断提高,最终的测试集的准确率为 0.9522,略低于 训练集上的准确率 0.9531,基本属于一个比较合理的训练结果。
5. 代码下载地址
DNN_Eager 代码下载链接地址(或扫描下面的二维码):
https://github.com/SciSharp/TensorFlow.NET-Tutorials/blob/master/PracticeCode/DNN_Eager/DNN_Eager/Program.cs
DNN_Keras 代码下载链接地址(或扫描下面的二维码):
https://github.com/SciSharp/TensorFlow.NET-Tutorials/blob/master/PracticeCode/DNN_Keras/DNN_Keras/Program.cs