【论文解读】ICLR2023 TimesNet: TEMPORAL 2D-VARIATION MODELING FOR GENERAL TIME SERIES ANALYSIS

一、摘要

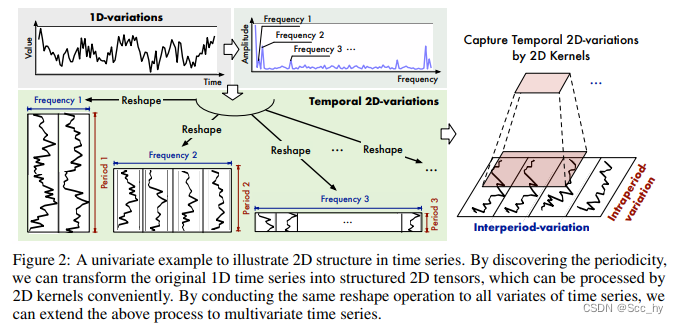
之前的方法都是尝试直接用1维时间序列进行预测序列、分类等任务。本文提出timesNet，基于多周期将时间序列从1维空间扩展到2维空间，这种变换可以将周期内和周期间的变化分别嵌入到2D张量的列和行中，2D张量易于用kernel进行特征提取。

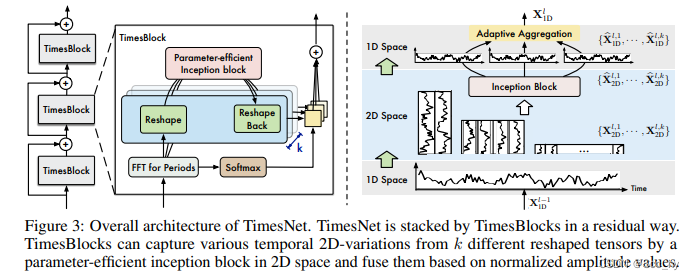
文中提出了将TimesBlock作为时间序列分析的任务通用主干的TimesNet。TimesBlock可以自适应地发现多周期性，并通过参数有效的起始块从变换后的2D张量中提取复杂的时间变化。

并在五个主流任务（包括短期和长期预测、插补、分类、异常检测）中取得sota的结果

二、简介

时序数据分析：

实时序列通常具有多个周期性，如天气观测的日变化和年变化，电力消耗的周变化和季度变化
每个时间点的变化不仅受其相邻区域的时间模式（周期内变化）的影响，而且与相邻周期的变化（周期间变化）高度相关。
对于没有明确周期性的时间序列，其变化将以周期内变化为主，相当于具有无限周期长度的时间序列。（这类数据理论上很难进行长期预测）

贡献：

受多周期性和周期内及周期间复杂相互作用的启发，我们找到了一种时间变化建模的模块化方法。
- 笔者思考：没有考虑到特定的人为因素的影响。
提出了具有TimesBlock的TimesNet来发现多个周期，并通过inceptionV1模块从转换的的2D张量中提取时间2D变化特征。
在五个主流时间序列分析任务中实现一致的SOTA。包括详细而深刻的可视化

三、TimesNet模型框架

3.1 时序从1D转变成2D

在这里插入图片描述
每个时间点都涉及两种类型的时间变化，即期内变化和期间变化。
首先基于傅里叶分析找到序列的多个周期
$\bf{A} = Avg(Amp(FFT(X_{1D}))), \{f_1, f_2, ..., f_k\}=\underset{f_* \in \{1, ..., \lceil \frac{T}{2}\rceil\}}{arg\ Topk} (A), p_i = \lceil \frac{T}{f_i}\rceil, i \in \{1, .., k\} \ \ (1)$
可以简写成
$A, \{f_1, ..., f_k\}, \{p_1, ..., p_k\}=Period(X_{1D}) \ \ \ (2)$

$f_i$ : 频率
$p_i = \lceil \frac{T}{f_i}\rceil$ : 一个周期长度

将 1D 时序 $X_{1D} \in \mathcal{R}^{T \times C}$ 转换成 2D 张量：
$X^{i}_{2D} = Reshape_{p_i, f_i}(Padding(X_{1D})), i \in \{1, ..., k\}$

$Padding(\cdot)$ 是将时间序列沿时间维度扩展0以使其兼容 $Reshape_{p_i, f_i}(\cdot)$
- row: $p_i$
- column: $f_i$
$X^{i}_{2D} \in \mathcal{R}^{T\times C}$ ：基于周期- $f_i$ 装换的第i个时序张量
获取一些列 2D 张量 $\{ X^{1}_{2D}, ..., X^{k}_{2D} \}$

code:

def FFT_for_Period(x, k=2):
    # [B, T, c]
    xf = torch.fft.rfft(x, dim=1)
    # find period by amplitudes
    freq_list = abs(xf).mean(0).mean(-1)
    freq_list[0] = 0
    _, top_list = torch.topk(freq_list, k)
    top_list = top_list.detach().cpu().numpy()
    period = x.shape[1] // top_list
    return period, abs(xf).mean(-1)[:, top_list]


period_list, period_weight = FFT_for_Period(x, 5)
res = []
for i in range(5):
    period = period_list[i]
    ## padding
    if (seq_len + pred_len) % period != 0:
        length = ( ((seq_len + pred_len) // period) + 1) * period
        padding = torch.zeros([x.shape[0], (length - ((seq_len + pred_len))), x.shape[2]]).to(x.device)
        out = torch.cat([x, padding], dim=1)
    else:
        length = seq_len + pred_len
        out = x 

    ## Reshape  1D -> 2D 
    ### [B, one-period series-len, period-dim, N-feature dim] ->
    ### [B, N-feature dim, one-period series-len, period-dim]
    out = out.reshape(B, length // period, period, N).permute(0, 3, 1, 2).contiguous()
    print(f"\n[ {i} (period={period}) ] 1D -> 2D: ", out.shape)

转换成2D后用2D的卷积核来提取特征
在这里插入图片描述

3.2 TimesBlock

基于residual方式构建 timesBlock
在这里插入图片描述
$X_{1D}^0 = Embed(X_{1D}),\ \ X_{1D}^0 \in \mathcal{R}^{T\times d_{model}}$ -->
$X^{l}_{1D} = TimesBlock(X^{l-1}_{1D}) +X^{l-1}_{1D}, \ \ X^{l}_{1D} \in \mathcal{R}^{T\times d_{model}}$

3.2.1 获取2维张量

和3.1中的描述一致

$A^{l-1},\{f_1,...,f_k\},\{p_1, ..., p_k\}=Period(X^{l-1}_{1D})$
$X_{2D}^{l, i}=Reshape_{p_i, f_i}(Padding(X^{l-1}_{1D})), i\in \{1, ..., k\}$
$\hat{X}_{2D}^{l, i}=Inception(X^{l, i}_{2D}), i\in \{1, ..., k\}$
$\hat{X}_{1D}^{l, i}=Trunc(Reshape_{1, p_i\times f_i}(\hat{X}_{2D}^{l, i})), i\in \{1, ..., k\}$
- $X_{2D}^{l, i} \in \mathcal{R}^{p_i \times f_i \times d_{model}}$

seq_len = 96
label_len = 0 
pred_len = 96  

# 1 capturing temporal 2D-varations
## Period
B, T, N = enc_out.size()
x = enc_out
period_list, period_weight = FFT_for_Period(x, 5)
period_list, period_weight.shape

res = []
for i in range(5):
    period = period_list[i]
    ## padding
    if (seq_len + pred_len) % period != 0:
        length = ( ((seq_len + pred_len) // period) + 1) * period
        padding = torch.zeros([x.shape[0], (length - ((seq_len + pred_len))), x.shape[2]]).to(x.device)
        out = torch.cat([x, padding], dim=1)
    else:
        length = seq_len + pred_len
        out = x 

    ## Reshape  1D -> 2D 
    ### [B, one-period series-len, period-dim, N-feature dim] ->
    ### [B, N-feature dim, one-period series-len, period-dim]
    out = out.reshape(B, length // period, period, N).permute(0, 3, 1, 2).contiguous()
    print(f"\n[ {i} (period={period}) ] 1D -> 2D: ", out.shape)
    ## Inception 2D conv: 
    ## channel first   conv on  pic-(one-period series-len, period-dim)
    # channel[d_model] -> 6核-conv, 累加求平均 -> channel[d_ff]  -> GELU
    # channel[d_ff]    -> 6核-conv, 累加求平均 -> channel[d_model] 
    conv = nn.Sequential(
        Inception_Block_V1(configs.d_model, configs.d_ff, num_kernels=configs.num_kernels),
        nn.GELU(),
        Inception_Block_V1(configs.d_ff, configs.d_model, num_kernels=configs.num_kernels)
    ).to(device)
    out = conv(out)
    print(f"[ {i} (Inception 2D) ] 2D -> \hat_2D: ", out.shape)
    # 转回1D -> [B, one-period series-len, period-dim, N-feature dim] -> [B, -1, N]
    out = out.permute(0, 2, 3, 1).reshape(B, -1, N)
    res.append(out[:, :(seq_len + pred_len), :])

print_str = """
[ 0 (period=96) ] 1D -> 2D:  torch.Size([32, 4, 2, 96])
[ 0 (Inception 2D) ] 2D -> \hat_2D:  torch.Size([32, 4, 2, 96])

[ 1 (period=4) ] 1D -> 2D:  torch.Size([32, 4, 48, 4])
[ 1 (Inception 2D) ] 2D -> \hat_2D:  torch.Size([32, 4, 48, 4])

[ 2 (period=13) ] 1D -> 2D:  torch.Size([32, 4, 15, 13])
[ 2 (Inception 2D) ] 2D -> \hat_2D:  torch.Size([32, 4, 15, 13])

[ 3 (period=2) ] 1D -> 2D:  torch.Size([32, 4, 96, 2])
[ 3 (Inception 2D) ] 2D -> \hat_2D:  torch.Size([32, 4, 96, 2])

[ 4 (period=3) ] 1D -> 2D:  torch.Size([32, 4, 64, 3])
[ 4 (Inception 2D) ] 2D -> \hat_2D:  torch.Size([32, 4, 64, 3])
"""

3.2.2 自适应地聚合表示(周期权重之和)

振幅A可以反映所选择的频率和周期的相对重要性

$\hat{A}_{f_1}^{l-1}, ..., \hat{A}_{f_k}^{l-1}=Softmax(A_{f_1}^{l-1}, ..., A_{f_k}^{l-1})$
$X_{1D}^l = \sum_{i=1}^{k}\hat{A}_{f_i}^{l-1} \times \hat{X}_{1D}^{l, i}$

# 2 adaptively aggregating representations
res = torch.stack(res, dim=-1) # 32, 264, 4, 5
print(res.shape)
# adaptive aggregation
period_weight = F.softmax(period_weight, dim=1)
print(period_weight.shape)
# [32, 5] -> [32, 264, 4, 5]
period_weight = period_weight.unsqueeze(1).unsqueeze(1).repeat(1, T, N, 1)
print(period_weight.shape)
# [32, 336, 4, 5] -> [32, 264, 4]
res = torch.sum(res * period_weight, -1)
# residual connection
res = res + x
print(res.shape)

print_str = """
torch.Size([32, 192, 4, 5])
torch.Size([32, 5])
torch.Size([32, 192, 4, 5])
torch.Size([32, 192, 4])
"""

四、实例

全部code可以看笔者github: timesNet_prime_stepByStep

论文中对五个主流时间序列分析任务一一进行了实现和比对。这里笔者仅仅针对时间长短期时序预测进行复现。

-	描述
使用数据	`ETT-small/ETTh1.csv`
数据概况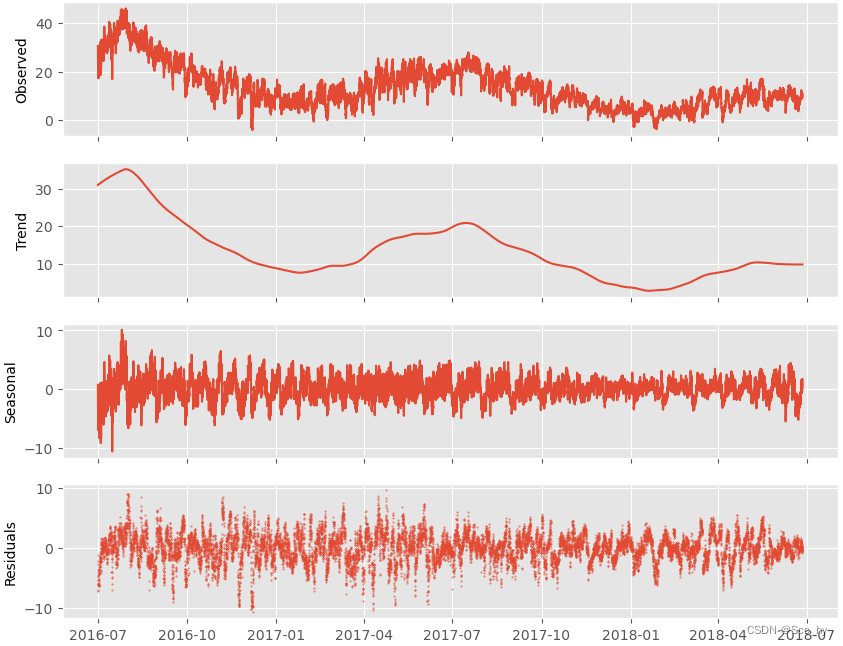

数据拆分	训练12个月，验证4个月，测试4个月
输入序列长度	`seq_len = 96`
预测序列长度	`pred_len = 96`

4.1 Dataset & DataLoader

这里我们延续论文的中开启数据归一化: scale=True，进行timeenc将日期字段拆分成[HourOfDay, DayOfWeek, DayOfMonth, DayOfYear]并归一化到[-0.5, 0.5]
返回值：

序列数据: seq_x
预测目标: seq_y len(seq_y) = 0(label_len) + pred_len)
序列数据对应的时间特征: seq_x_mark
- 数据范围: [-0.5, 0.5]
- 数据维度: 4, [HourOfDay, DayOfWeek, DayOfMonth, DayOfYear]
预测目标对应的时间特征: : seq_y_mark len(seq_y) = 0(label_len) + pred_len)

a = time_features(pd.to_datetime(df['date'].values[:2]), freq='h').T
print(a,  df['date'].values[:2])
print_str = """
[[-0.5         0.16666667 -0.5        -0.00136986]
 [-0.45652174  0.16666667 -0.5        -0.00136986]]
array(['2016-07-01 00:00:00', '2016-07-01 01:00:00'], dtype=object)
"""


class Dataset_ETT_hour(Dataset):
    def __init__(self, root_path, flag='train', size=[24 * 4 * 4, 24 * 4, 24 *4], features='S', data_path='ETTh1.csv',
                 target='OT', scale=True, timeenc=0, freq='h', seasonal_patterns=None):
        # from figure -> the data didn't have seasonal_patterns
        # size [seq_len, label_len, pred_len]
        self.seq_len = size[0]
        self.label_len = size[1]
        self.pred_len = size[2]
        assert flag in ['train', 'val', 'test']
        type_map = {'train': 0, 'val': 1, 'test': 2}
        self.set_type = type_map[flag]
        
        self.features = features
        self.target = target 
        self.scale = scale
        self.timeenc = timeenc
        self.freq = freq 
        
        self.root_path = root_path
        self.data_path = data_path
        self.__read_data__()
        
    def __read_data__(self):
        self.scaler = StandardScaler()
        df_raw = pd.read_csv(f'{self.root_path}{os.sep}{self.data_path}').sort_values(by='date', ignore_index=True)
        base_ = 30 * 24
        border1s = [
            0,
            12 * base_ - self.seq_len, 
            (12 + 4) * base_ - self.seq_len
        ]
        border2s = [
            12 * base_, 
            (12 + 4) * base_, 
            (12 + 8) * base_
        ]
        border1 = border1s[self.set_type]
        border2 = border2s[self.set_type]
        print(self.set_type, f"{border1} -> {border2}")
        # multi series
        if self.features in ['M', 'MS']: 
            cols_data = df_raw.columns[1:]
            df_data = df_raw[cols_data]
        # single series
        elif self.features == 'S':
            df_data = df_raw[[self.target]]

        if self.scale:
            train_data = df_data[border1s[0]:border2s[0]]
            self.scaler.fit(train_data.values)
            data = self.scaler.transform(df_data.values)
        else:
            data = df_data.values
        
        df_stamp = df_raw[['date']][border1:border2]
        df_stamp['date'] = pd.to_datetime(df_stamp.date)
        if self.timeenc == 0:
            df_stamp['month'] = df_stamp.date.apply(lambda row: row.month, 1)
            df_stamp['day'] = df_stamp.date.apply(lambda row: row.day, 1)
            df_stamp['weekday'] = df_stamp.date.apply(lambda row: row.weekday(), 1)
            df_stamp['hour'] = df_stamp.date.apply(lambda row: row.hour, 1)
            data_stamp = df_stamp.drop(['date'], 1).values
        if self.timeenc == 1: # encoded as value between [-0.5, 0.5]
            data_stamp = time_features(pd.to_datetime(df_stamp['date'].values), freq=self.freq)
            data_stamp = data_stamp.transpose(1, 0)

        self.data_x = data[border1:border2]
        self.data_y = data[border1:border2]
        self.data_stamp = data_stamp
    
    def __getitem__(self, index):
        s_begin = index
        s_end = s_begin + self.seq_len
        r_begin = s_end - self.label_len
        r_end = r_begin + self.label_len + self.pred_len

        seq_x = self.data_x[s_begin:s_end]
        seq_y = self.data_y[r_begin:r_end]
        seq_x_mark = self.data_stamp[s_begin:s_end]
        seq_y_mark = self.data_stamp[r_begin:r_end]
        return seq_x, seq_y, seq_x_mark, seq_y_mark

    def __len__(self):
        return len(self.data_x) - self.seq_len - self.pred_len + 1

    def inverse_transform(self, data):
        return self.scaler.inverse_transform(data)

4.2 model

4.2.1 batch normalize

means = x_enc.mean(1, keepdim=True).detach()
x_enc = x_enc - means
stdev = torch.sqrt(
    torch.var(x_enc, dim=1, keepdim=True, unbiased=False) + 1e-5
)
x_enc /= stdev

4.2.2 embedding

embedding = value_embedding(series_data) + temporal_embedding(encode_time) + position_embedding(series_data)

value_embedding: nn.Conv1d(in_channels=c_in, out_channels=d_model, kernel_size=3, padding=padding, padding_mode='circular', bias=False)
temporal_embedding: nn.Linear(d_inp, d_model)
position_embedding: odd-sin(div_term) even-cos(div_term)
- div_term = (torch.arange(0, d_model, 2).float() * -math.log(10000.0) / d_model).exp()

d_model = 4
enc_embedding = DataEmbedding(1, d_model, 'timeF', 'h', drop=0.1).to(device)
predict_linear = nn.Linear(seq_len, pred_len + seq_len).to(device)
## value_embedding [nn.Conv1d] 
#   + temporal_embedding [nn.Linear(d_inp, d_model)] 
#   + position_embedding [odd-sin(div_term) even-cos(div_term)]
enc_out = enc_embedding(x_enc, x_mark_enc)
print(enc_out.shape)
enc_out = predict_linear(enc_out.permute(0, 2, 1)).permute(0, 2, 1)
print(enc_out.shape)

4.2.3 predict_linear时序数据线性变换

self.predict_linear = nn.Linear(
                self.seq_len, self.pred_len + self.seq_len)

enc_out = self.predict_linear(enc_out.permute(0, 2, 1)).permute(0, 2, 1)

4.2.4 TimesNet

同3.2的描述


class TimesBlock(nn.Module):
    def __init__(self, configs):
        super(TimesBlock, self).__init__()
        self.seq_len = configs.seq_len
        self.pred_len = configs.pred_len
        self.k = configs.top_k
        # parameter-efficient design
        self.conv = nn.Sequential(
            Inception_Block_V1(configs.d_model, configs.d_ff, 
                               num_kernels=configs.num_kernels),
            nn.GELU(),
            Inception_Block_V1(configs.d_ff, configs.d_model, 
                               num_kernels=configs.num_kernels)
        )
    
    def forward(self, x):
        B, T, N = x.size()
        period_list, period_weight = FFT_for_Period(x, self.k)
        res = []
        for i in range(self.k):
            period = period_list[i]
            # padding
            if (self.seq_len + self.pred_len) % period != 0:
                length = ( 
                          ((self.seq_len + self.pred_len) // period) + 1) * period
                padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), 
                                       x.shape[2]]).to(x.device)
                out = torch.cat([x, padding], dim=1)
            else:
                length = self.seq_len + self.pred_len
                out = x 
            
            ## Reshape  1D -> 2D 
            ### [B, one-period series-len, period-dim, N-feature dim] ->
            ### [B, N-feature dim, one-period series-len, period-dim]
            out = out.reshape(B, length // period, period, N).permute(0, 3, 1, 2).contiguous()
            # Inception: 2D conv: from 1d varation to 2d variation
            ## channel first   conv on  pic-(one-period series-len, period-dim)
            # channel[d_model] -> 6-conv, stack, mean -> channel[d_ff]  -> GELU
            # channel[d_ff]    -> 6-conv, stack, mean -> channel[d_model] 
            out = self.conv(out)
            # reshape back
            out = out.permute(0, 2, 3, 1).reshape(B, -1, N)
            res.append(out[:, :(self.seq_len + self.pred_len), :])
        res = torch.stack(res, dim=-1)
        # adaptive aggregation
        period_weight = F.softmax(period_weight, dim=1)
        period_weight = period_weight.unsqueeze(1).unsqueeze(1).repeat(1, T, N, 1)
        res = torch.sum(res * period_weight, -1)
        # residual connection
        return res + x

self.model = nn.ModuleList([TimesBlock(configs) for _ in range(configs.e_layers)])

for i in range(self.layer):
    enc_out = self.layer_norm(self.model[i](enc_out))

4.2.5 projection 和 De-Normalize

最后再做一次线性变换，然后再转回数据

self.projection = nn.Linear(
                configs.d_model, configs.c_out, bias=True)
# project back
dec_out = self.projection(enc_out)

# De-Normalization from Non-stationary Transformer
dec_out = dec_out * stdev[:, 0, :].unsqueeze(1).repeat(1, self.pred_len + self.seq_len, 1)
dec_out = dec_out + means[:, 0, :].unsqueeze(1).repeat(1, self.pred_len + self.seq_len, 1)

4.2.6 模型整体结构


class Model(nn.Module):
    """
    Paper link: https://openreview.net/pdf?id=ju_Uqw384Oq
    """
    def __init__(self, configs):
        super(Model, self).__init__()
        self.configs = configs
        self.task_name = configs.task_name
        self.seq_len = configs.seq_len
        self.label_len = configs.label_len
        self.pred_len = configs.pred_len
        self.model = nn.ModuleList([TimesBlock(configs) for _ in range(configs.e_layers)])
        self.enc_embedding = DataEmbedding(configs.enc_in, configs.d_model, configs.embed, configs.freq, configs.dropout)
        self.layer = configs.e_layers
        self.layer_norm = nn.LayerNorm(configs.d_model)
        if self.task_name in ['long_term_forecast', 'short_term_forecast']:
            # forcast  his + future
            self.predict_linear = nn.Linear(
                self.seq_len, self.pred_len + self.seq_len)
            self.projection = nn.Linear(
                configs.d_model, configs.c_out, bias=True)

    def forecast(self, x_enc, x_mark_enc, x_dec, x_mark_dec):
        # Normalization from Non-stationart Transformer
        means = x_enc.mean(1, keepdim=True).detach()
        x_enc = x_enc - means
        stdev = torch.sqrt(
            torch.var(x_enc, dim=1, keepdim=True, unbiased=False) + 1e-5
        )
        x_enc /= stdev
        # embedding
        enc_out = self.enc_embedding(x_enc, x_mark_enc)
        # operate in timeseries
        enc_out = self.predict_linear(enc_out.permute(0, 2, 1)).permute(0, 2, 1)
        # TimesNet
        for i in range(self.layer):
            enc_out = self.layer_norm(self.model[i](enc_out))
        
        # project back
        dec_out = self.projection(enc_out)
        
        # De-Normalization from Non-stationary Transformer
        dec_out = dec_out * stdev[:, 0, :].unsqueeze(1).repeat(1, self.pred_len + self.seq_len, 1)
        dec_out = dec_out + means[:, 0, :].unsqueeze(1).repeat(1, self.pred_len + self.seq_len, 1)
        return dec_out
        
    def forward(self, x_enc, x_mark_enc, x_dec, x_mark_dec, mask=None):
        if self.task_name in ['long_term_forecast', 'short_term_forecast']:
            dec_out = self.forecast(x_enc, x_mark_enc, x_dec, x_mark_dec)
            return dec_out[:, -self.pred_len:, :]  # [B, L, D]
        return None

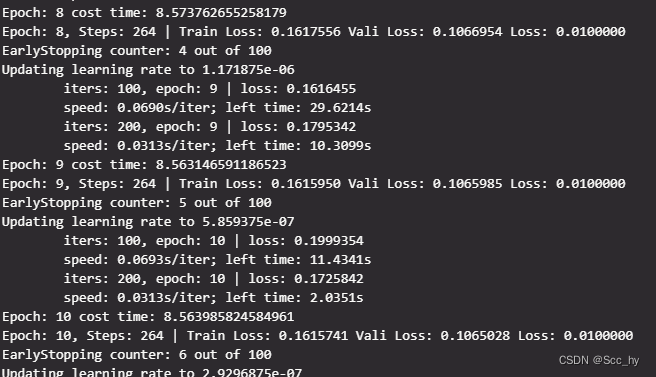
4.3 模型训练

参数配置

args = Namespace(
    task_name='long_term_forecast',
    is_training=1,
    model_id='ETTh1_96_96',
    model='TimesNet',
    data='ETTh1',
    root_path='~/Downloads/Datas/ETDataset/ETT-small/',
    data_path='ETTh1.csv',
    features='S', # M
    target='OT',
    freq='h',
    scale=True,
    checkpoints='./checkpoints/',
    seq_len=96, 
    label_len=0,
    pred_len=96,
    seasonal_patterns='Monthly',
    top_k=5,
    num_kernels=6,
    enc_in=1, # 7 7 7
    dec_in=1,
    c_out=1,
    d_model=6, # 16
    e_layers=3, # 2
    d_ff=12,
    dropout=0.1,
    embed='timeF',
    # embed='fixed',
    output_attention=False,
    num_workers=10,
    itr=1,
    train_epochs=10,
    batch_size=32,
    patience=100,
    learning_rate=1.5e-4, #1e-4,
    loss='MSE',
    lradj='type1',
    use_amp=False
)

在这里插入图片描述

4.4 模型预测简单查看及总结

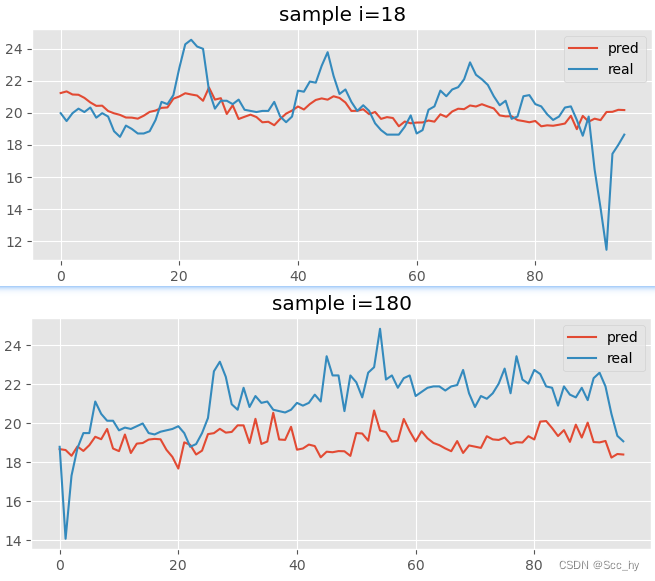
从数据总览中可以看出我们的训练数据其实存在年度的周期（7月数据较高），但是我们输入序列仅仅4天其实很难捕捉这种总的周期和趋势。所以可以遇见的是，在设定96的输入长度的时候不论什么模型其预测效果应该都是一般的。
但是在论文中模型的rmse均在1一下，查看了源码发现，论文的rmse是在数据归一化后的计算出的值，不过其比较的模型也同样在归一化后计算出来的。

所以实际上模型的评估指标是偏好的，不过在统一标准下，进行比较得出的结论应该还是有效的。
下图是测试集中某一个样本段的预测结果，可以看出对周期性的捕捉还是可以的，但是实际拟合效果并不是十分理想。
在这里插入图片描述
从算法框架搭建的基础（基于频率将数据从1D转2D）出发，我们可以将周期性较强的数据尝试使用TimesNet进行落地应用。也可以仅仅将TimesBlock拿出来，加入到现有的预测框架中，因为我们还需要其影响因素特征的数据（如天气、节假日等）

五、结论和未来工作

本文提出了时间网作为时间序列分析的任务通用基础模型。受多周期性的启发，TimesNet可以通过模块化架构来解析复杂的时间变化，并通过参数有效的起始块来捕捉2D空间中的周期内和周期间变化。
未来工作：

探索时间序列中的大规模预训练方法
TimesNet作为骨干，通常可以为广泛的下游任务带来好处。