数据结构--二叉树随记

二叉树主要分为四类：满二叉树、完全二叉树、二叉搜索树、平衡二叉搜索树。

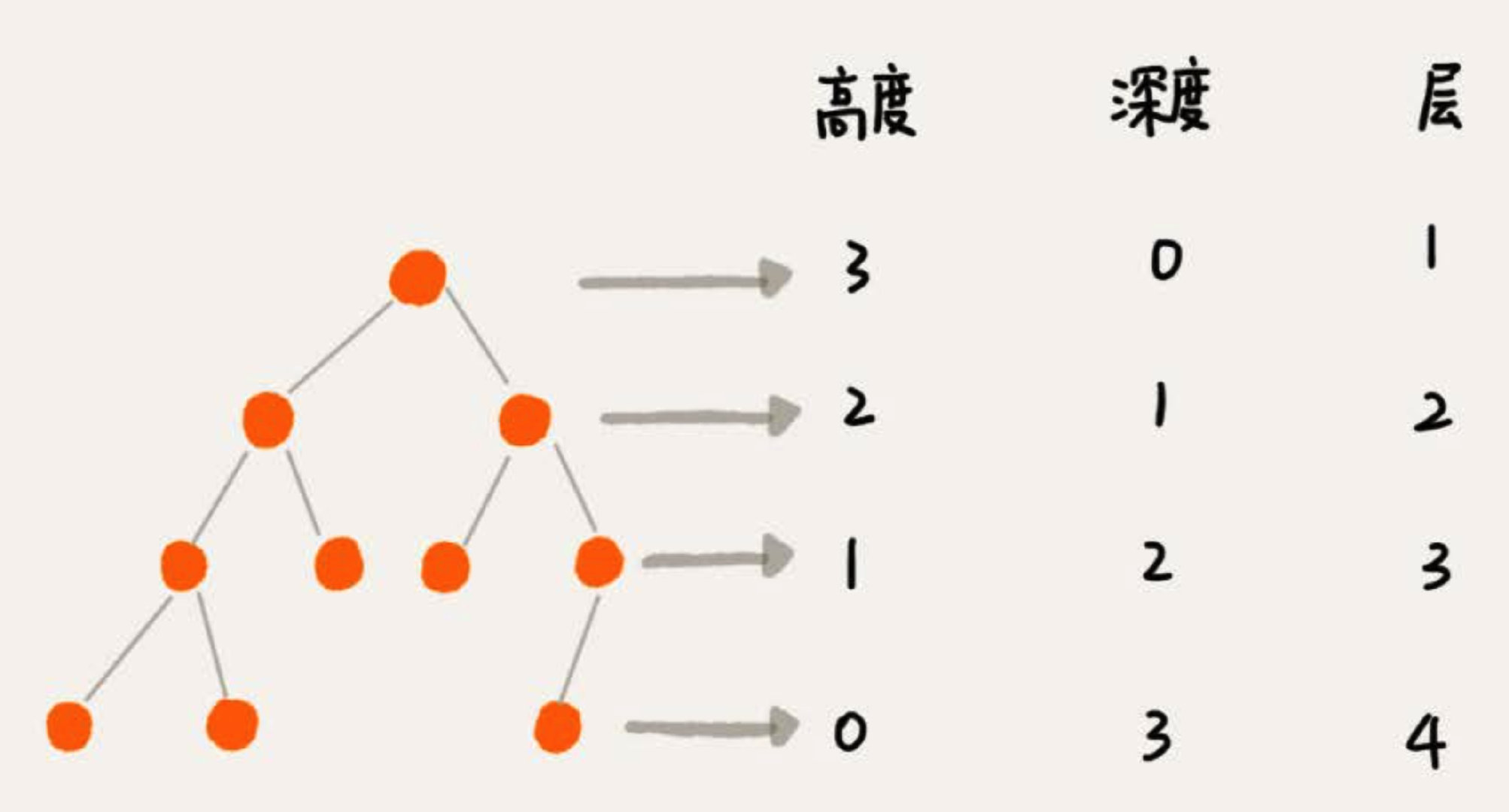
高度,深度,层

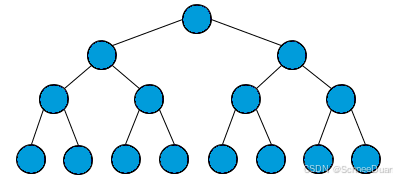
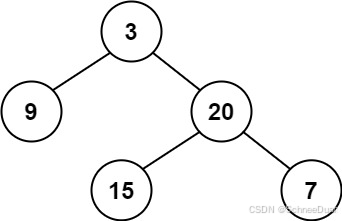
满二叉树

满二叉树就是每一层节点都是满的，整棵树像一个正三角形：

满二叉树有个优势，就是它的节点个数很好算。假设深度为 h，那么总节点数就是 2^h - 1，等比数列求和。

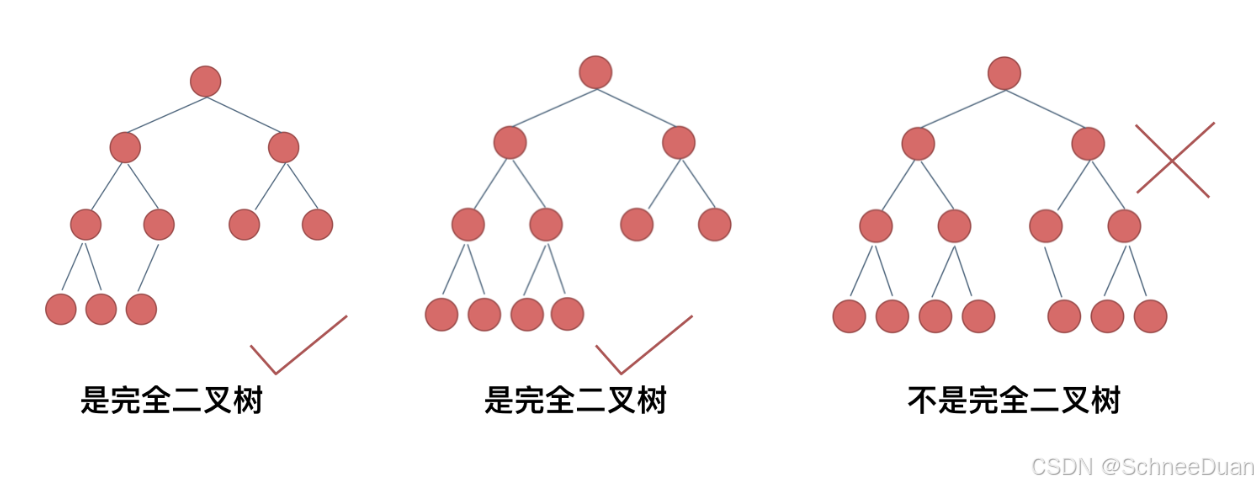
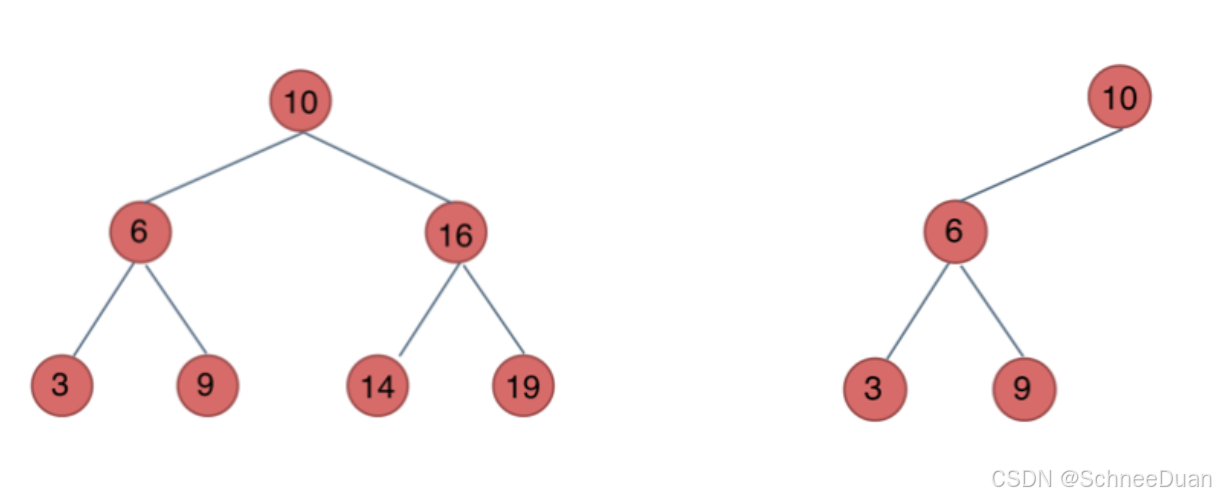
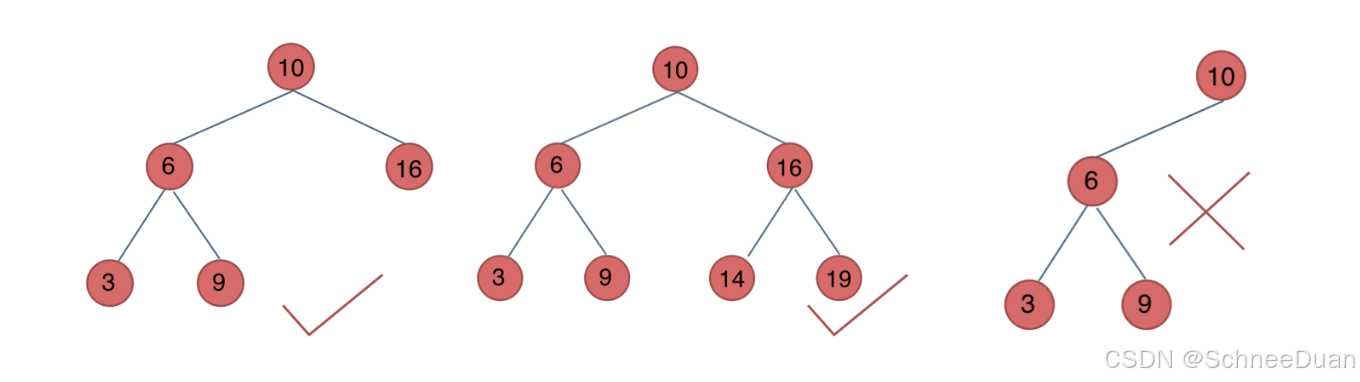
完全二叉树

完全二叉树是指，除了最后一层，二叉树其他每层都必须是满的，且最下面一层的节点都集中在该层最左边的若干位置：

如下：

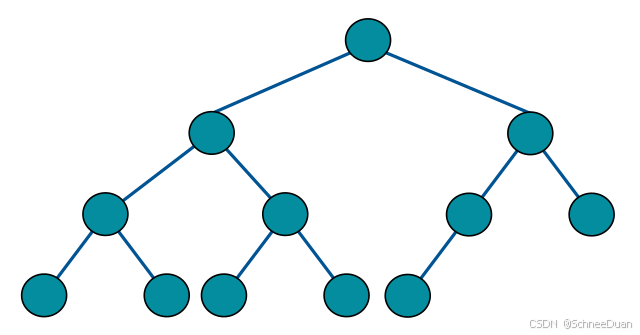
平衡二叉树

平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。如下图：

二叉搜索树

前面介绍的树，都没有数值的，而二叉搜索树是有数值的了，二叉搜索树是一个有序树。

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树

可以记成【左小右大】：

平衡二叉搜索树

它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树：

C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是log(n)。

二叉树的存储方式

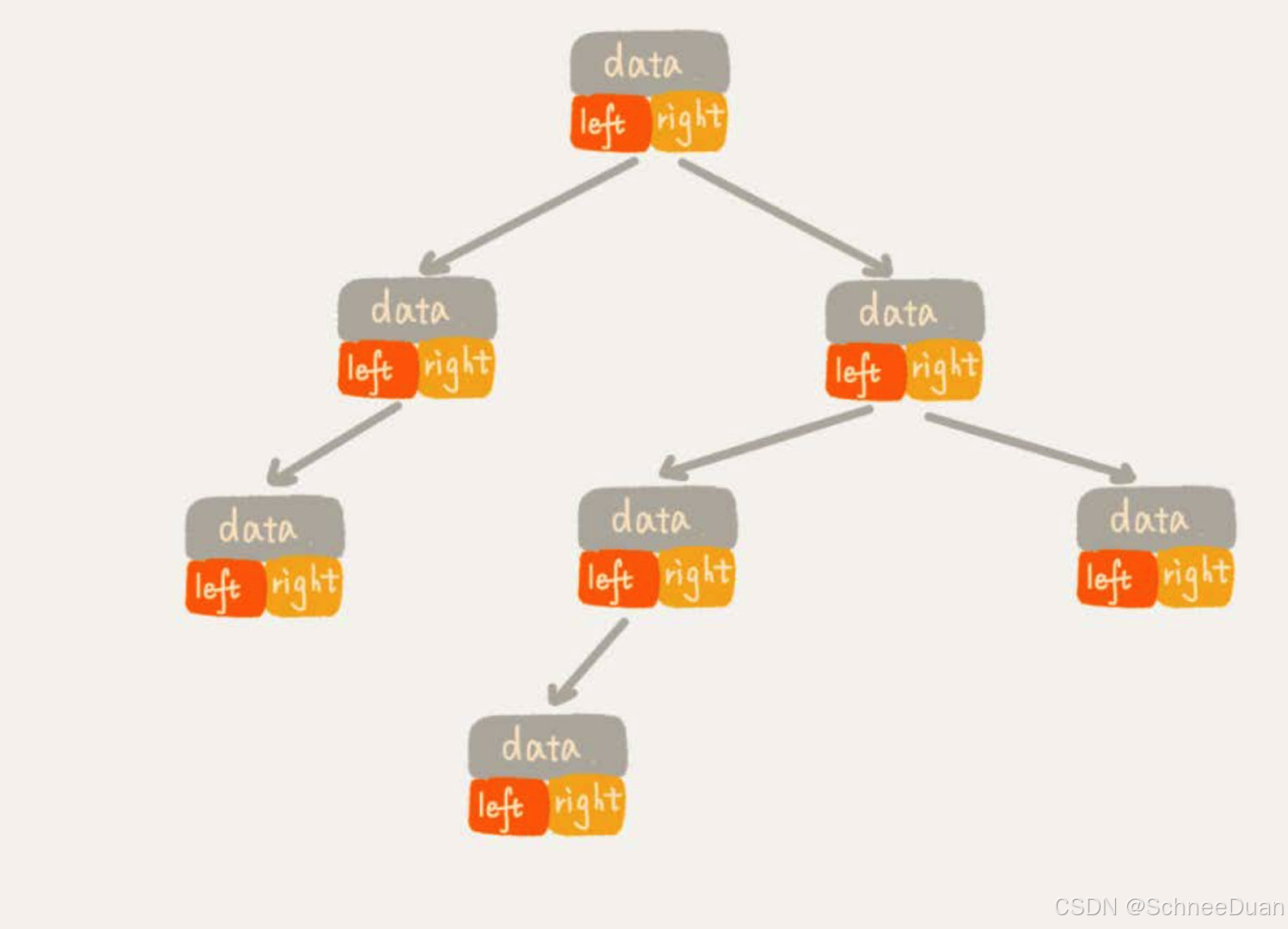
链式存储

基于指针或者引用的二叉链式存储法：

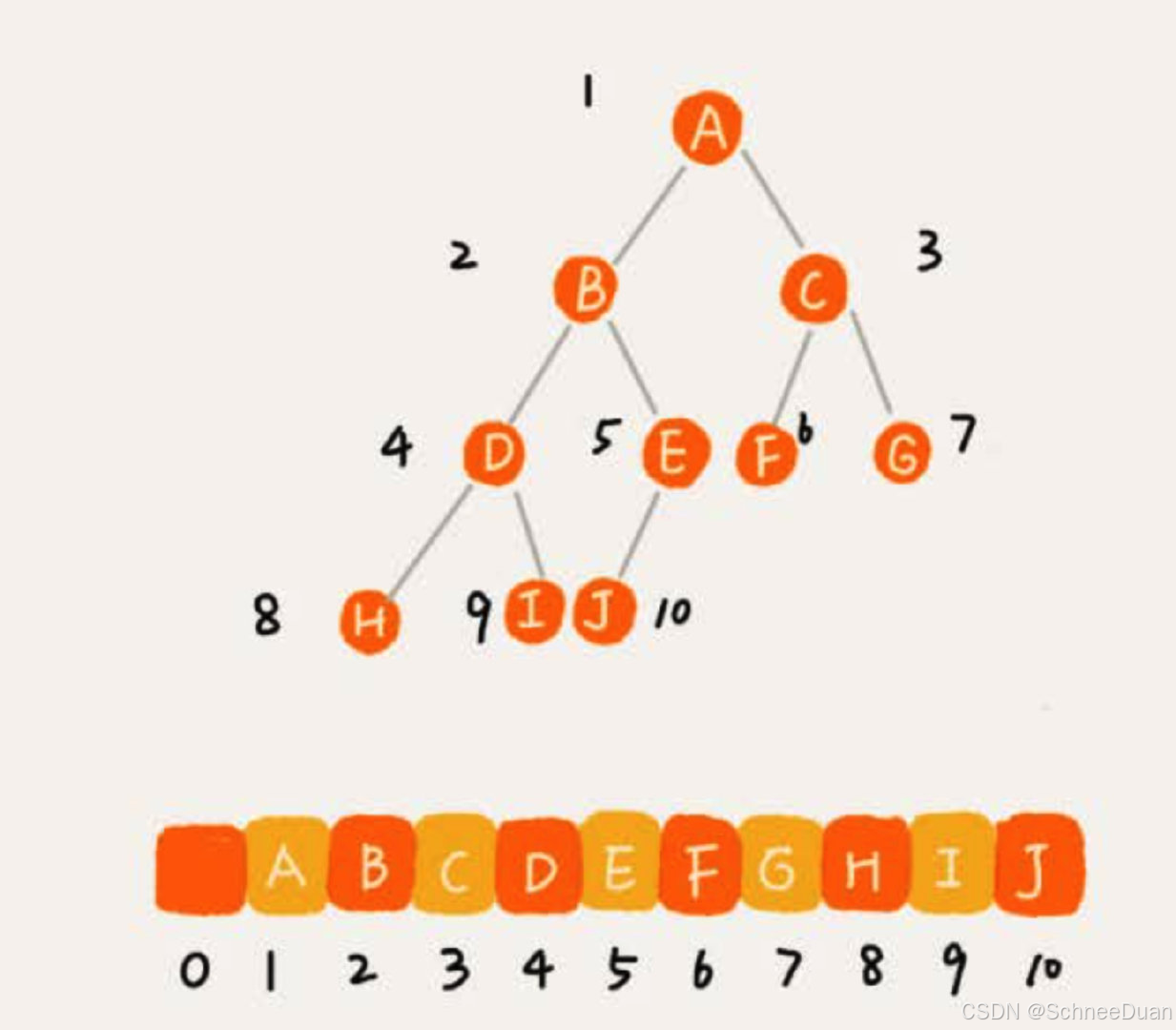
顺序存储

基于数组的顺序存储法：

如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

二叉树遍历方式

二叉树主要有两种遍历方式：

深度优先遍历：先往深走，遇到叶子节点再往回走。
广度优先遍历：一层一层的去遍历。

其中：

深度优先遍历
- 前序遍历（递归法，迭代法）
- 中序遍历（递归法，迭代法）
- 后序遍历（递归法，迭代法）
广度优先遍历
- 层次遍历（迭代法）

深度优先遍历

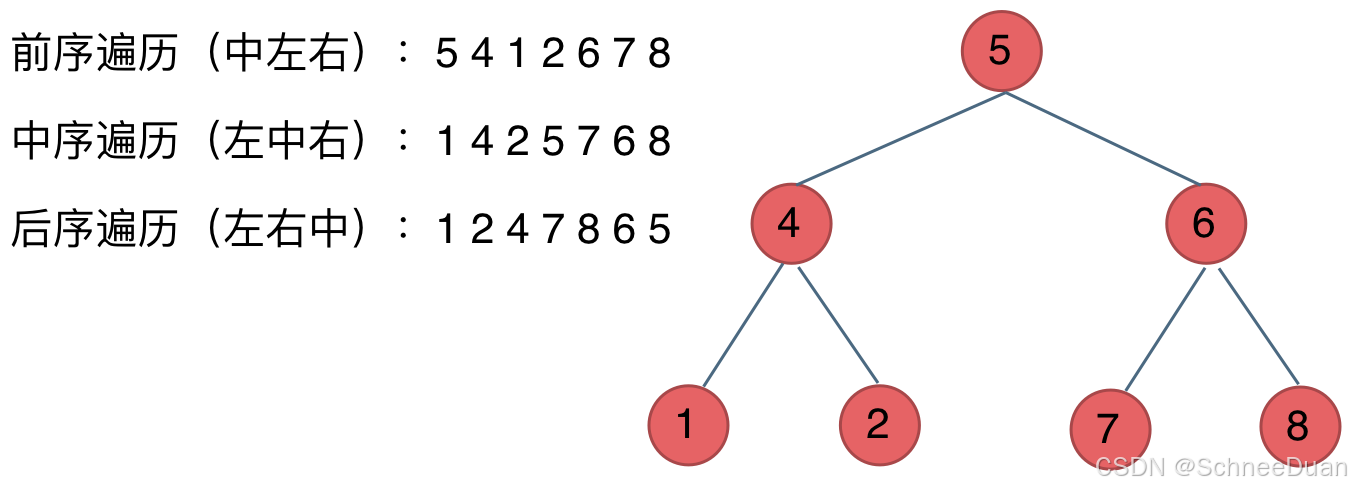
前序遍历：中左右
中序遍历：左中右
后序遍历：左右中

这里的左、中、右指的是子树，而不是节点。

二叉树的定义（cpp）：

  struct TreeNode {
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right){}
  };

//TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right){}为构造函数 
//有构造函数，定义初始值为9的节点：

TreeNode* a = new TreeNode(9);


// 你也可以这样构建一棵二叉树：
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->right->left = new TreeNode(5);
root->right->right = new TreeNode(6);

// 构建出来的二叉树是这样的：
//     1
//    / \
//   2   3
//  /   / \
// 4   5   6

二叉树的遍历(深度优先遍历)

递归

三要素：

确定递归函数的参数和返回值： 确定哪些参数是递归的过程中需要处理的，那么就在递归函数里加上这个参数，并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
确定终止条件： 写完了递归算法, 运行的时候，经常会遇到栈溢出的错误，就是没写终止条件或者终止条件写的不对，操作系统也是用一个栈的结构来保存每一层递归的信息，如果递归没有终止，操作系统的内存栈必然就会溢出。
确定单层递归的逻辑： 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。

前序遍历：

144. 二叉树的前序遍历 - 力扣（LeetCode）

demo

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

 //前序遍历 : 中 左 右
class Solution {
public:
    void traversal(TreeNode* cur,vector<int>& vec){
        if(cur == nullptr) return;
        vec.push_back(cur->val); //中
        traversal(cur->left,vec); //左
        traversal(cur->right,vec); //右
    }


    vector<int> preorderTraversal(TreeNode* root) {
            vector<int>vec;
            traversal(root,vec);
            return vec;
    }
};

中序遍历：

94. 二叉树的中序遍历 - 力扣（LeetCode）

demo

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 //中序遍历： 左中右
class Solution {
public:

    void traversal(TreeNode* cur,vector<int>& vec){
        if(cur == nullptr) return;
        traversal(cur->left,vec); //左
        vec.push_back(cur->val); //中      
        traversal(cur->right,vec); //右
    } 

    vector<int> inorderTraversal(TreeNode* root) {
        vector<int>vec;
        traversal(root,vec);
        return vec;
    }
};

后序遍历：

145. 二叉树的后序遍历 - 力扣（LeetCode）

demo

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 //后序遍历 左右中
class Solution {
public:
    void tranversal(TreeNode* cur,vector<int>& vec){
        if(cur == nullptr) return;
        tranversal(cur->left,vec); //左
        tranversal(cur->right,vec); //右
        vec.push_back(cur->val); //中
    }
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int>vec;
        tranversal(root,vec);
        return vec;
    }
};

N叉树前序遍历：

589. N叉树的前序遍历

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    void transeve(Node* cur,vector<int>& vec){
        if(cur == NULL) return;
        vec.push_back(cur->val);
        int childrenSize = cur->children.size();
        for(int i=0;i<childrenSize;i++){
            transeve(cur->children[i],vec);
        }
    }
    vector<int> preorder(Node* root) {
        vector<int>result;
        transeve(root,result);
        return result;
    }
};

迭代

前序遍历：

其实可以这么理解：前序遍历是 “中左右”，那么此时我应该先弹出“中”---也就是根节点本身，此时根节点必须在顶层，所以左右子树先不放进去，我们把左右子树连带着其儿子一起分别看成是两个整体，由于栈的特性是先进后出，我们只能需要顶层的元素，所以按照“中左右”的顺序，右应该在左的前面进入，所以我们的顺序应该是：“中”进、“中”出、“右进”、“左进”、“左出”、“右出”。这里我们把左右子树包括其儿子一起看成了左右两个整体，当“右进”等一系列操作的时候，我们在其整体中循环以上操作即可。

由此可以写出前序遍历的迭代法代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 //迭代法：栈实现前序遍历：中 左 右 
 //因为先进后出 所以先放中、中出、右进、左进、左出、右出
 //模拟递归思想 顺序变了而已
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int>result;
        stack<TreeNode*>st;
        if(root == nullptr) return result;
        st.push(root);
        while(!st.empty()){
            TreeNode* cur = st.top();
            st.pop();
            result.push_back(cur->val); //中
            if(cur->right) st.push(cur->right); //右
            if(cur->left) st.push(cur->left); //左
        }

        return result;
    }
};

二叉树前序遍历 - 力扣（LeetCode）

中序遍历：

其实就是一直遍历左边（“左”）然后到NULL的时候再取出栈中的根节点（“中”），然后跟节点的右边（“右”）。

中序遍历的迭代法代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 //迭代法 栈实现中序遍历： 左 中 右
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int>result;
        stack<TreeNode*>st;
        if(root == nullptr) return result;
        TreeNode* cur = root;
        while(!st.empty() || cur != nullptr){
            if(cur != nullptr){
                st.push(cur);
                cur = cur->left;
            }else{
                cur = st.top();
                st.pop();//此时的节点已经到左子树根节点了，左子树A的左儿子是AL,右儿子是AR,没有第四层了,这时候左儿子没有左右子树了，但是仍然会查找一遍是否有左右子树，发现都没有后，取st.top()时，就是左子树A了，这时候才去查找左子树A的右儿子AR。循环重复。
                result.push_back(cur->val);
                cur = cur->right;
            }

        }

        return result;
    }
};

二叉树的中序遍历 - 力扣（LeetCode）

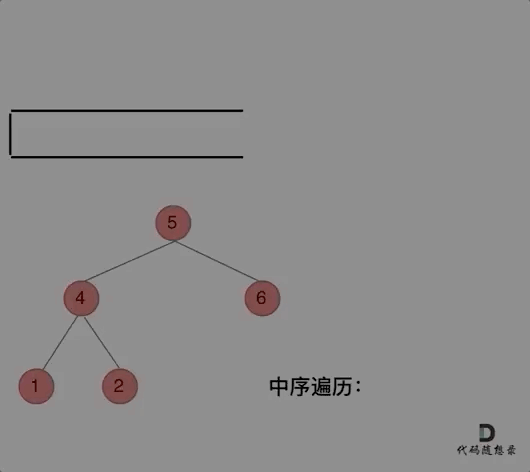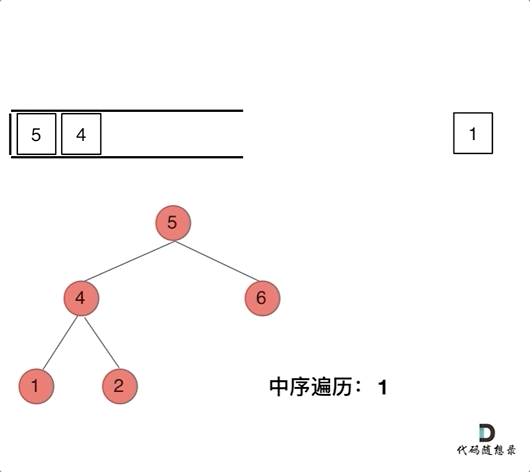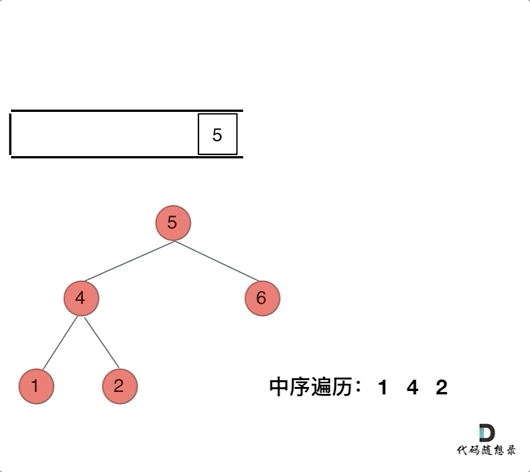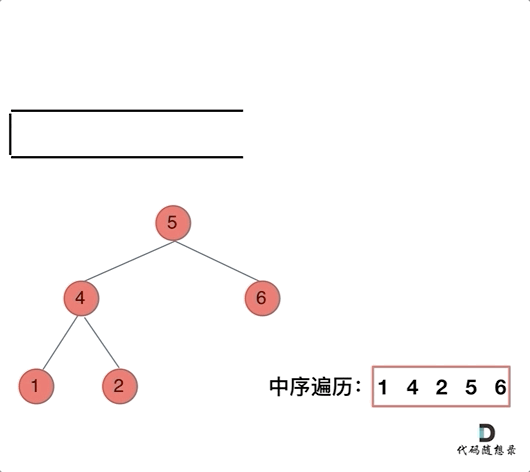
后序遍历：

再来看后序遍历，先序遍历是中左右，后序遍历是左右中，那么我们只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后在反转result数组，输出的结果顺序就是左右中了，如下图：

后序遍历的迭代法代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 //迭代法 栈实现后序遍历： 先-- 中 右 左 、接着反转 、左 右 中 。所以在先序遍历（中左右）的基础上改就可以了。
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int>result;
        stack<TreeNode*>st;
        if(root == nullptr) return result;
        st.push(root);
        while(!st.empty()){
            TreeNode* cur = st.top();
            st.pop();
            result.push_back(cur->val); //中
            if(cur->left) st.push(cur->left); //右
            if(cur->right) st.push(cur->right); //左
        }
        reverse(result.begin(),result.end()); //反转 变成: 左 右 中
        return result;

    }
};

二叉树后序遍历 - 力扣（LeetCode）

二叉树的遍历（广度优先遍历）

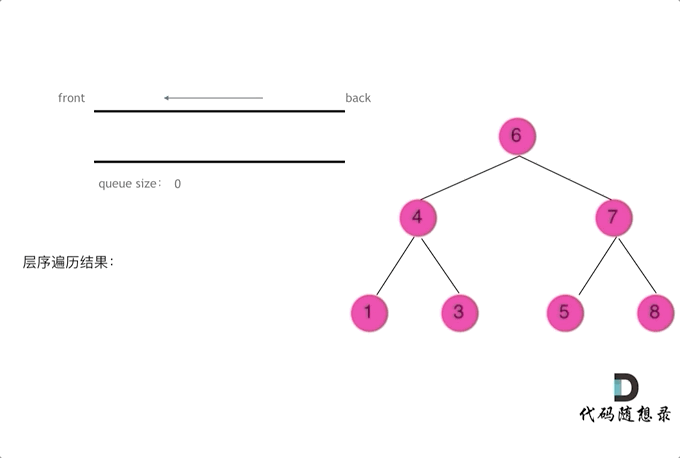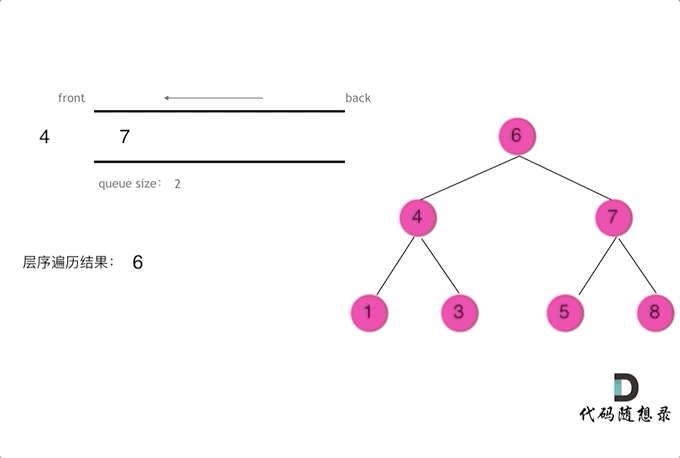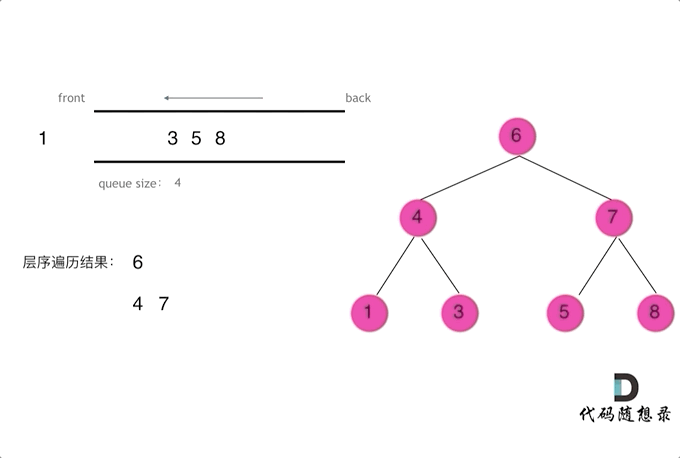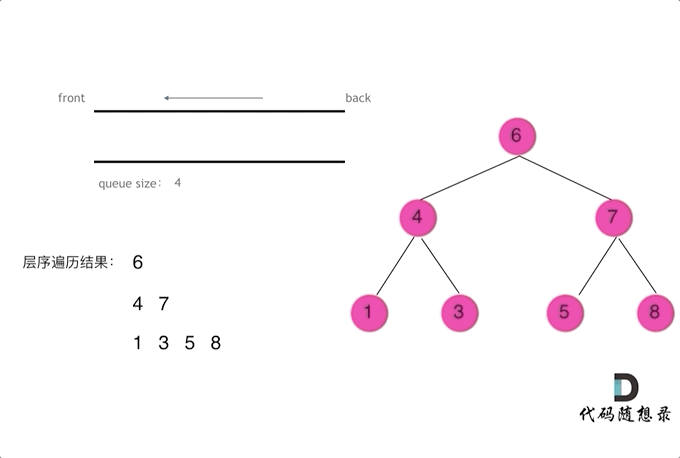
层序遍历：

层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

我们看下代码实现：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*>q;
        vector<vector<int>>result;
        if(root == nullptr) return result;
        q.push(root);
        while(!q.empty()){
        int size = q.size();   //size必须为固定值，不能用q.size()，q.size()是不断变化的
        vector<int>vec; //用里面的vector记录每一层的数值
        for(int i=0;i<size;i++){ //一个节点出去后 就把其左右子树放进队列中
            TreeNode* cur = q.front();
            q.pop();
            vec.push_back(cur->val);
            if(cur->left) q.push(cur->left);
            if(cur->right) q.push(cur->right);
        }
        result.push_back(vec); //外面的vector记录全部层
        }
        return result;
    }
};

102. 二叉树的层序遍历 - 力扣（LeetCode）

N叉树层序遍历：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

//注意Node的children是vector属性，所以我们可以遍历其vector，也是板子题，然后就是，cur的每个children都需要放进队列中，因为这样我们才能去children中寻找是否还有子节点！！
class Solution {
public:
    vector<vector<int>> levelOrder(Node* root) {
        queue<Node*>q;
        vector<vector<int>>result;
        if(root == NULL) return result;
        q.push(root);
        while(!q.empty()){
            vector<int>vec;
            int size = q.size();
            for(int i=0;i<size;i++){
                Node* cur = q.front();
                q.pop();
                vec.push_back(cur->val);
                for(int j = 0;j<cur->children.size();j++){
                    if(cur->children[j])q.push(cur->children[j]);
                }
            }
            result.push_back(vec);
        }
        return result;


    }
};

N叉树层序遍历 - 力扣（LeetCode）

需要注意的是，我们需要把每个节点的子节点都放进queue中，这样我们才可以在queue中查找改子节点是否还有左右子树！！！此外，时刻注意size是必须的，因为此时的size是纪律这一层的节点数。

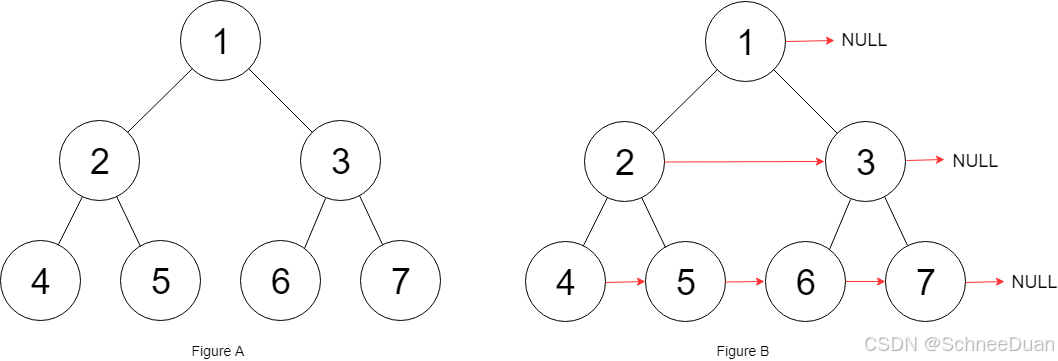
填充每个节点的下一个右侧节点指针：

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。如下图：

还是在层序遍历的基础上分类讨论：节点是最后一个节点 or 不是最后一个节点

代码：

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;

    Node() : val(0), left(NULL), right(NULL), next(NULL) {}

    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}

    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/
// 还是在层序遍历的基础上 分类讨论：节点是最后一个节点 or 不是最后一个节点
// 注意判断queue是否为空！
class Solution {
public:
    Node* connect(Node* root) {
        queue<Node*> q;
        if (root == NULL)
            return NULL;
        q.push(root);
        while (!q.empty()) {
            int size = q.size();
            for (int i = 0; i < size; i++) {
                Node* cur = q.front();
                q.pop();
                if (i == size - 1) {
                    cur->next = NULL;
                } else if (i != size - 1 && !q.empty()) {//在同一层考虑即可 因为前面已经把当前节点弹出了：q.pop(),所以可以直接获取同一层的右边节点：q.front()
                    cur->next = q.front();
                }
                if (cur->left)
                    q.push(cur->left);
                if (cur->right)
                    q.push(cur->right);
            }
        }
        return root;
    }
};

填充每个节点的下一个右侧节点指针 - 力扣（LeetCode）

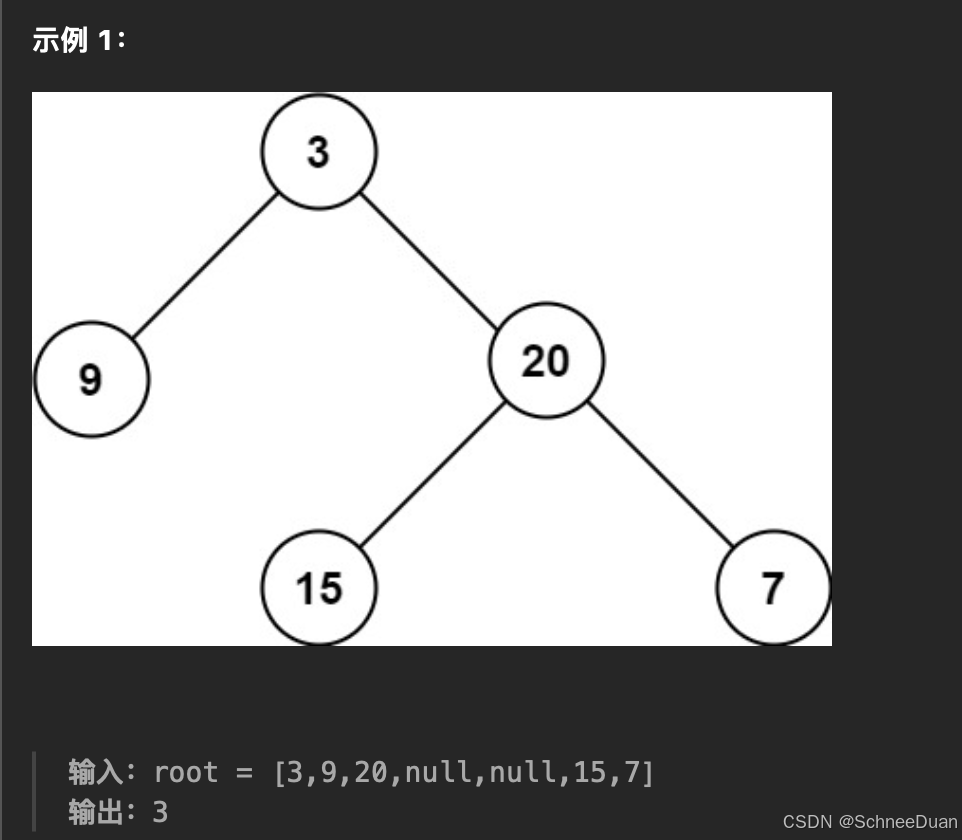
二叉树的最大深度:

给定一个二叉树 root ，返回其最大深度。二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        queue<TreeNode*> q;
        if (root == nullptr)
            return 0;
        q.push(root);
        int ans = 0;
        while (!q.empty()) {
            int size = q.size();
            for (int i = 0; i < size; i++) {
                TreeNode* cur = q.front();
                q.pop();
                if (cur->left)
                    q.push(cur->left);
                if (cur->right)
                    q.push(cur->right);
            }
            ans++;
        }
        return ans;
    }
};

思路很简单，只需要在每层结束后ans++即可。

二叉树的最小深度

给定一个二叉树，找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
// 层次遍历 判断当前节点是否没有左右子树 如果没有的话 当前节点就是最短路径的节点
// 每层都用cell++
class Solution {
public:
    int minDepth(TreeNode* root) {
        queue<TreeNode*> q;
        if (root == nullptr)
            return 0;
        q.push(root);
        int cell = 0;
        int ans = 0;
        bool isok = false;
        while (!q.empty()) {
            int size = q.size();
            cell++;
            for (int i = 0; i < size; i++) {
                TreeNode* cur = q.front();
                q.pop();
                if (cur->left)
                    q.push(cur->left);
                if (cur->right)
                    q.push(cur->right);
                if (cur->left == nullptr && cur->right == nullptr) {
                    ans = cell;
                    isok = true;
                    break;
                }
            }
            if (isok)
                break;
        }
        return ans;
    }
};

递归法同样可以解决：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
// 递归
class Solution {
public:
    int dfs(TreeNode* cur) {
        if (cur == nullptr) {
            return 0;
        }
        if (cur->left == nullptr && cur->right != nullptr) {
            return dfs(cur->right) + 1;
        }
        if (cur->left != nullptr && cur->right == nullptr) {
            return (dfs(cur->left) + 1);
        }
        return min(dfs(cur->right), dfs(cur->left)) + 1;
    }
    int minDepth(TreeNode* root) { return dfs(root); }
};

总结：二叉树的层序遍历需要借助队列实现。

题目：

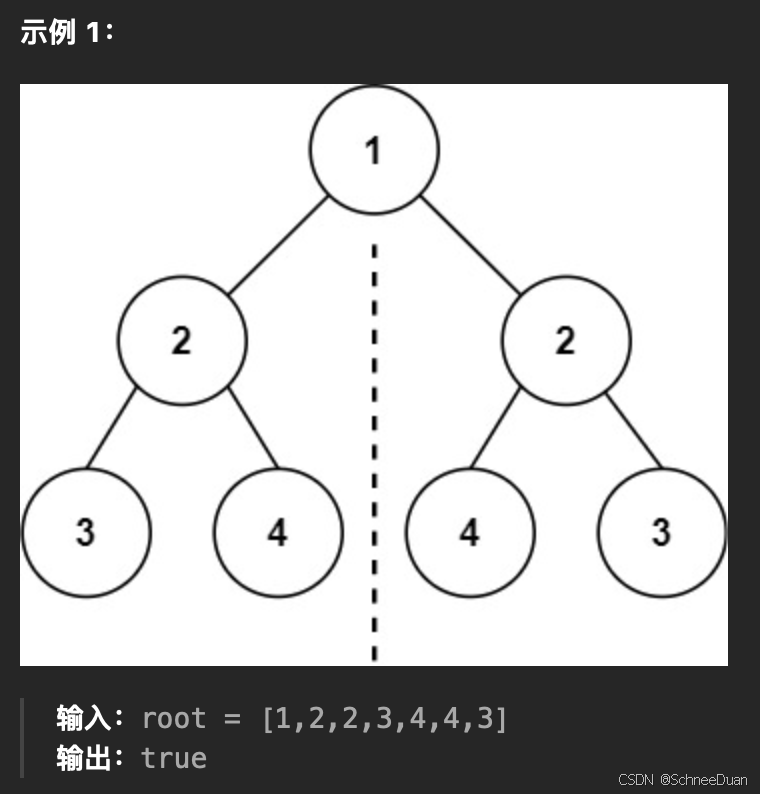
对称二叉树

看是否轴对称，迭代+分类讨论：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
// 分类讨论 将左右子树（对称的）放在相邻 弹出的时候 做判断
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        queue<TreeNode*> q;

        if (root == nullptr)
            return true;
        q.push(root->left);
        q.push(root->right);
        while (!q.empty()) {
            TreeNode* nodeLeft = q.front();
            q.pop();
            TreeNode* nodeRight = q.front();
            q.pop();
            if(nodeLeft == nullptr && nodeRight == nullptr) continue;

            //分类讨论
            if (nodeLeft != nullptr &&
                nodeRight != nullptr && nodeLeft->val != nodeRight->val) {
                return false;
            }else if(nodeLeft == nullptr && nodeRight != nullptr){
                return false;
            }else if(nodeLeft != nullptr && nodeRight == nullptr){
                return false;
            }
            
            //注意顺序 要对称！！！！
            q.push(nodeLeft->left);
            q.push(nodeRight->right);
            q.push(nodeLeft->right);
            q.push(nodeRight->left);
        }

        return true;
    }
};

注意入队顺序！！！

对称二叉树 - 力扣（LeetCode）

完全二叉树的节点个数

给出一个完全二叉树，求出该树的节点个数。

示例 1：

输入：root = [1,2,3,4,5,6]
输出：6

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
 //迭代法
// class Solution {
// public:
//     int countNodes(TreeNode* root) {
//         queue<TreeNode*>q;
//         if(root == nullptr) return 0;
//         q.push(root);
//         int ans = 0;
//         while(!q.empty()){
//             int size = q.size();
//             for(int i = 0;i < size;i++){
//                 TreeNode* cur = q.front();
//                 q.pop();
//                 ans++;
//                 if(cur->left) q.push(cur->left);
//                 if(cur->right) q.push(cur->right);
//             }

//         }
//         return ans;

//     }
// };
//递归法
class Solution {
public:
    int transeve(TreeNode* cur) {
        if (cur == nullptr)
            return 0;
        return transeve(cur->left) + transeve(cur->right) + 1;
    }
    int countNodes(TreeNode* root) {
        int ans = transeve(root);
        return ans;
    }
};

完全二叉树的节点个数 - 力扣（LeetCode）

主要是递归不熟。。。。

是否是平衡二叉树

给定一个二叉树，判断它是否是 “平衡二叉树” 、即任意节点的左右子树高度差是否总是小于等于1。

这里涉及到高度与深度的选择：

我们来分析一下：这道题求的是左右子树的高度差的绝对值不超过1，很明显求的是“高度”，或者我们换个思路，这道题我们可以从子节点反向递归回父节点，从子树往上递归+1，父节点取左右子树的高度最大值+1，然后如果左右子树的差值大于1的话，直接返回-1即可，这里需要用到后序遍历（左右中）。

一般来说：

求高度用后序遍历
求深度用前序遍历

递归code：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 //可以看出是求高度的 -> 我们可以反向思维 从子树往上递归+1 父节点取左右子树的高度最大值+1 然后如果左右子树的差值大于1的话 直接返回-1即可 这里需要用到后序遍历
 //后序遍历 左右中 
 //求高度一般是后序遍历 求深度是前序遍历
class Solution {
public:
    int transerve(TreeNode* cur){
        if(cur == nullptr) return 0;
        int leftHeight = transerve(cur->left); //左
        int rightHeight = transerve(cur->right); //右
        if(leftHeight == -1)return -1;
        if(rightHeight == -1)return -1;
        //中
        if(abs(leftHeight - rightHeight) > 1){
            return -1;
        }else{
            return max(leftHeight,rightHeight) + 1;
        }
    }
    bool isBalanced(TreeNode* root) {
        if(root == nullptr) return true;
        if(transerve(root) == -1){
            return false;
        }
        return true;
    }
};

这里顺便巩固一下递归。

首先用递归我们要明确一下递归三部曲：

明确递归函数的参数和返回值：参数：当前传入节点。返回值：以当前传入节点为根节点的树的高度。
明确终止条件：递归的过程中依然是遇到空节点了为终止，返回0，表示当前节点为根节点的树高度为0。也可以这么认为：当遇到没有左右子树的节点的时候，也就是说这个cur->left、cur->right都为NULL的话，此时cur->left、cur->right都返回0，表明这个空节点的高度为0，而cur高度为1。
明确单层递归的逻辑：如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢？当然是其左子树高度和其右子树高度的差值。

代码递归的意思就是说，先遍历左右子树，然后根据左右子树返回的高度值来进行逻辑判断。

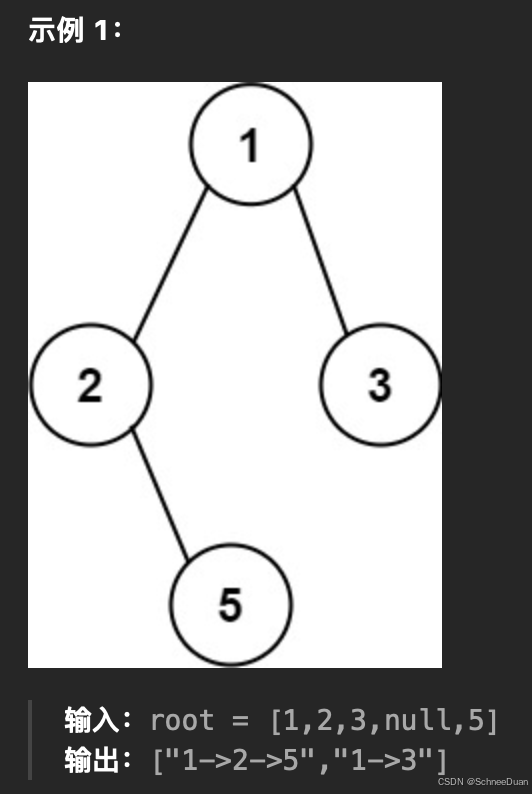
二叉树所有路径

递归+回溯

这道题根据输出结果可知用dfs前序遍历是最方便的，本体难点涉及到需要用path记录路径并且回溯。既然是dfs，用递归是最方便的（相比于栈的迭代法）。

首先给出本题code：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
// 递归 + 回溯
// 前序遍历
class Solution {
public:
    void transeve(TreeNode* cur, vector<int>& path, vector<string>& result) {
        if (cur == nullptr)
            return;
        // 中 ： 记录路径
        path.push_back(cur->val);
        // 终止条件 -> 当为叶节点时 返回路径结果
        if (cur->left == nullptr && cur->right == nullptr) {
            // int 转 string
            string pathString = "";
            for (int i = 0; i < path.size(); i++) {
                // int 转为 string
                pathString += to_string(path[i]);
                if (i != path.size() - 1) {
                    pathString += "->";
                }
            }
            // 将转换结果放进vector中
            result.push_back(pathString);
        }

        // 左
        if (cur->left) {
            transeve(cur->left, path, result);
            // 回溯
            path.pop_back();
        }
        // 右
        if (cur->right) {
            transeve(cur->right, path, result);
            // 回溯
            path.pop_back();
        }
    }
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        vector<int> path;
        if (root == nullptr)
            return result;
        transeve(root, path, result);
        return result;
    }
};

既然是递归的话，就还是按照递归三部曲：

明确参数和返回值：这里需要多一个path来记录路径，可以先用vector<int>来记录，对于结果的时候转换成string即可。
明确终止条件：求的是根节点到叶子节点的路径，而且还是前序遍历，那么肯定是以叶子节点为终止条件，即cur->left == nullptr && cur->right == nullptr。
明确单层递归逻辑：无非就是记录path，把此层值放进path中，并且需要回溯一下。

关于回溯：

首先记得，回溯一定要和递归放一起！！！！你左右递归的时候就要立刻回溯！！！

迭代法

个人觉得迭代法其实更好理解一些，code：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 //dfs前序遍历 栈迭代法实现
 //用两个栈 分别存“节点”和“走过的路径” 
 //两点注意： 
 /*
 一、栈的先进后出的 所以前序遍历（中左右）要改成 （中右左）
 二、路径沿用父节点的路径来进行相加
*/
class Solution {
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        stack<TreeNode*>st;
        stack<string>pathSt;
        vector<string>result;
        if(root == nullptr) return result;
        st.push(root);
        pathSt.push(to_string(root->val));
        while(!st.empty()){
            //取出节点的同时 也要取出节点路径
            TreeNode* cur = st.top();
            st.pop();
            string path = pathSt.top();
            pathSt.pop();
            if(cur->left == nullptr && cur->right == nullptr){
                result.push_back(path);
            }
            //右
            if(cur->right){
                st.push(cur->right);
                //沿用父节点的路径
                pathSt.push(path + "->" + to_string(cur->right->val));
            }
            //左
            if(cur->left){
                st.push(cur->left);
                //沿用父节点的路径
                pathSt.push(path + "->" + to_string(cur->left->val));
            }

        }

        return result;

    }
};

二叉树的所有路径 - 力扣（LeetCode）

路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false。

其实和二叉树所有路径的迭代法一样的，都是子节点继承父节点的某些东西。

code：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 //前序遍历 dfs栈迭代法 中 右 左
 //终止条件 此节点没有左右子树（到达最底层了）
 //两个栈 其中一个用来维护此节点的总值
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        stack<TreeNode*>st;
        stack<int>ve; //维护此节点的总值
        bool result = false;
        if(root == nullptr) return false;
        st.push(root);
        ve.push(root->val);
        while(!st.empty()){
            TreeNode* cur = st.top();
            st.pop();
            int nowValue = ve.top();
            ve.pop();
            //中
            if(!cur->left && !cur->right){
                if(nowValue == targetSum){
                    result = true;
                    break;
                }
            }
            //右
            if(cur->right){
                st.push(cur->right);
                ve.push(nowValue + cur->right->val); //继承父节点的值
            }
            //左
            if(cur->left){
                st.push(cur->left);
                ve.push(nowValue + cur->left->val);//继承父节点的值
            }

        }
        return result;


    }
};

路径总和 - 力扣（LeetCode）

左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。

dfs栈迭代法前序遍历：

用两个栈分别记录节点和节点是左子树还是右子树

终止条件->当此时的节点没有左右子树（即已经在最低层了），看此时的节点是左子树还是右子树

其实迭代法是一一对应的，每个点都会遍历一遍。

code：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 //前序遍历 dfs栈迭代法 中 右 左
 //用一个bool值判断此时是左子树还是右子树 终止条件是此时的节点没有左右子树（即已经在最低层了）
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
       stack<TreeNode*>st;
       //bool判断此时是左子树还是右子树
       stack<bool>lrSt;
       int result = 0;
       if(root == nullptr) return result;
        st.push(root);
        lrSt.push(false);//根节点不算叶子 所以是false
        while(!st.empty()){
            TreeNode* cur = st.top();
            st.pop();
            bool lr = lrSt.top();
            lrSt.pop();
            //中
            if(!cur->left && !cur->right && lr == true){
                result += cur->val;
            }
            //右
            if(cur->right){
                st.push(cur->right);
                lrSt.push(false);
            }
            //左
            if(cur->left){
                st.push(cur->left);
                lrSt.push(true);
            }

        }

        return result;

    }
};

左叶子之和 - 力扣（LeetCode）

从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

重点！！！

递归 + 切割

code：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 //用后序遍历（左右中）确定根节点 然后通过根节点在中序遍历（左中右）切割 然后左右分别递归
class Solution {
public:
    TreeNode* transeve(vector<int>& inorder,vector<int>& postorder){
        if (postorder.size() == 0) return NULL; //在函数里面要特判一次 返回空指针（最底部的叶子节点）！！！
        TreeNode* root = new TreeNode(postorder[postorder.size()-1]);
        if(postorder.size() == 1) return root;
        postorder.pop_back();
        TreeNode* cur = root;
        vector<int>leftInorder;
        vector<int>rightInorder;
        int i=0;
        for(;i<inorder.size();i++){
            if(inorder[i] == root->val){
                break;
            }else{
                leftInorder.push_back(inorder[i]);
            }
        }
        i++;
        for(;i<inorder.size();i++){
            rightInorder.push_back(inorder[i]);
        }
        vector<int>leftPostorder;
        vector<int>rightPostorder;
        for(i=0;i<leftInorder.size();i++){
            leftPostorder.push_back(postorder[i]);
        }
        
        for(;i<rightInorder.size() + leftInorder.size();i++){
            rightPostorder.push_back(postorder[i]);
        }

        //递归
        cur->left = transeve(leftInorder,leftPostorder);
        cur->right = transeve(rightInorder,rightPostorder);
        return root;

    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        return transeve(inorder,postorder);
    }
};

从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）

优化版code：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* transeve(vector<int>& inorder, vector<int>& postorder) {
        if (postorder.size() == 0)
            return nullptr;

        TreeNode* root = new TreeNode(postorder[postorder.size() - 1]);
        if (postorder.size() == 1)
            return root;
        TreeNode* cur = root;
        postorder.pop_back();
        int i = 0;
        for (i = 0; i < inorder.size(); i++) {
            if (inorder[i] == root->val) {
                break;
            }
        }
        vector<int> leftInorder(inorder.begin(), inorder.begin() + i);
        vector<int> rightInorder(inorder.begin() + i + 1, inorder.end());

        vector<int> leftPostoreder(postorder.begin(),
                                   postorder.begin() + leftInorder.size());
        vector<int> rightPostoreder(postorder.begin() + leftInorder.size(),
                                    postorder.end());

        cur->left = transeve(leftInorder, leftPostoreder);
        cur->right = transeve(rightInorder, rightPostoreder);

        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        return transeve(inorder, postorder);
    }
};

合并二叉树

两个队列同时遍历两个数注意分类讨论

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
 //用两个队列同时遍历两个树。以root1为主要的 最后返回的也是root1 
 
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        queue<TreeNode*> q1;
        queue<TreeNode*> q2;
        if (root1 == nullptr && root2 == nullptr)
            return nullptr;
        if (root1 != nullptr && root2 == nullptr)
            return root1;
        if (root1 == nullptr && root2 != nullptr)
            return root2;
        q1.push(root1);
        q2.push(root2);
        while (!q1.empty() || !q2.empty()) {
            TreeNode* cur1 = q1.front();
            q1.pop();
            TreeNode* cur2 = q2.front();
            q2.pop();
            //两个树节点都存在 直接相加
            if (cur1 != nullptr && cur2 != nullptr) {
                cur1->val += cur2->val;
            }
            //两个树的左节点都存在 左节点都放入队列中
            if (cur1->left != nullptr && cur2->left != nullptr) {
                q1.push(cur1->left);
                q2.push(cur2->left);
            }
            if (cur1->right != nullptr && cur2->right != nullptr) {
                q1.push(cur1->right);
                q2.push(cur2->right);
            }
            //root1的左节点没有的话 就把root2的左节点给root1
            if (cur1->left == nullptr && cur2->left != nullptr) {
                cur1->left = cur2->left;
            }
            //root1的右节点没有的话 就把root2的右节点给root1
            if (cur1->right == nullptr && cur2->right != nullptr) {
                cur1->right = cur2->right;
            }
        }
        return root1;
    }
};

合并二叉树 - 力扣（LeetCode）

验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

code：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
// 中序遍历 左中右
//注意 不能单纯的比较左节点小于中间节点，右节点大于中间节点就完事了。这是错的 应该是左子树和右子树

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode* cur = root;
        TreeNode* pre = NULL; // 记录前一个节点
        while (cur != nullptr || !st.empty()) {
            if (cur != NULL) {
                st.push(cur);
                cur = cur->left; // 左
            } else {
                cur = st.top(); // 中
                st.pop();
                if (pre != NULL && cur->val <= pre->val)
                    return false;
                pre = cur; // 保存前一个访问的结点

                cur = cur->right; // 右
            }
        }
        return true;
    }
};

98. 验证二叉搜索树 - 力扣（LeetCode）

关于二叉树的做题思路

首先先看是深度搜索还是广度搜索：

深度搜索dfs用递归 or 栈迭代。
广度搜索bfs用队列。

然后看是前中后序遍历：

Tips：栈的特性是先进后出所以有点特殊：前序遍历（中右左）、后序遍历（左右中）->栈的前序遍历的代码反转就是了。
递归三部曲牢记。

还有特殊的，双队列、双栈，建议把题目都再做一遍。。。。

参考：

代码随想录 (programmercarl.com)

力扣 (LeetCode) 全球极客挚爱的技术成长平台