目录
1.算法仿真效果
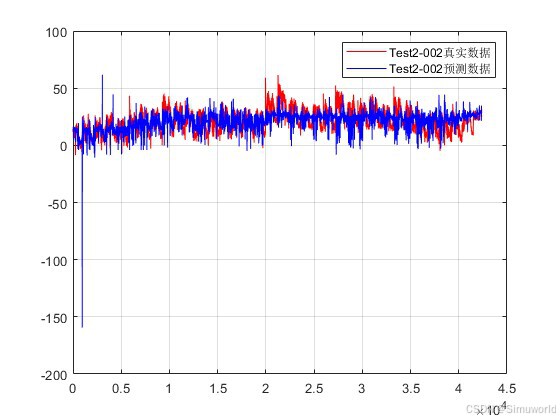
matlab2022a仿真结果如下:
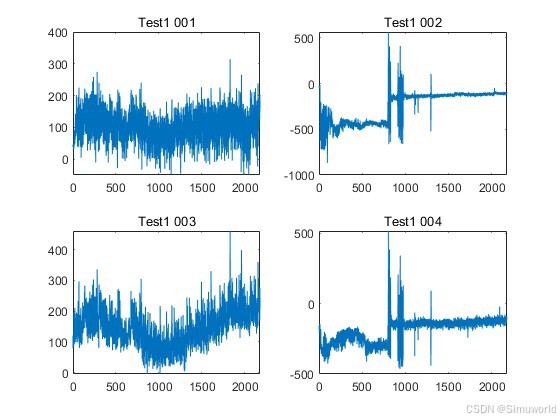
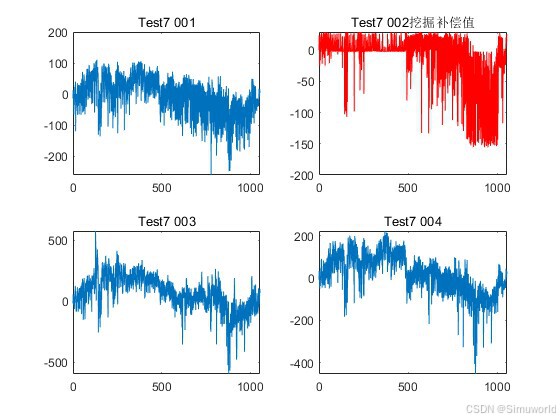
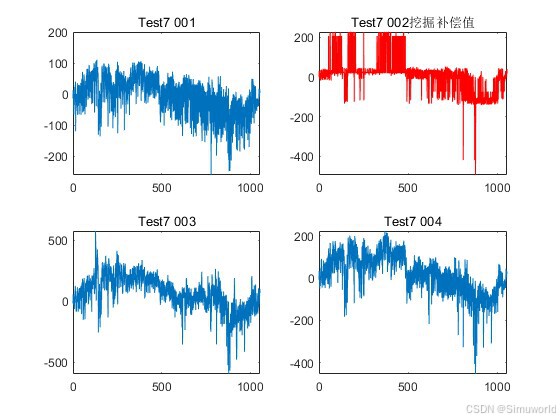
测试样本如下:
BP神经网络
rbf神经网络
GRNN广义回归神经网络
2.MATLAB源码
0002.............................................................................
Ker=400;%除以400,让数据都小于1,如果训练数据大于1,训练会错误
P1=[k1*Test1_001(:,2),k2*Test1_003(:,2),k3*Test1_004(:,2)]/Ker;%训练数据库合并
T1=[Test1_002(:,2)]/Ker;%目标值,将通道2的结果作为目标值
P2=[k1*Test2_001(:,2),k2*Test2_003(:,2),k3*Test2_004(:,2)]/Ker;%训练数据库合并
T2=[Test2_002(:,2)]/Ker;%目标值,将通道2的结果作为目标值
P6=[k1*Test6_001(:,2),k2*Test6_003(:,2),k3*Test6_004(:,2)]/Ker;%训练数据库合并
T6=[Test6_002(:,2)]/Ker;%目标值,将通道2的结果作为目标值
%数据合并,一起参与训练
P = [P1;P2;P6];
T = [T1;T2;T6];
%进行BP神经网络训练
net1 = func_BP_train(P',T');
%进行BP神经网络预测
T1pre = sim(net1,P1');
figure;
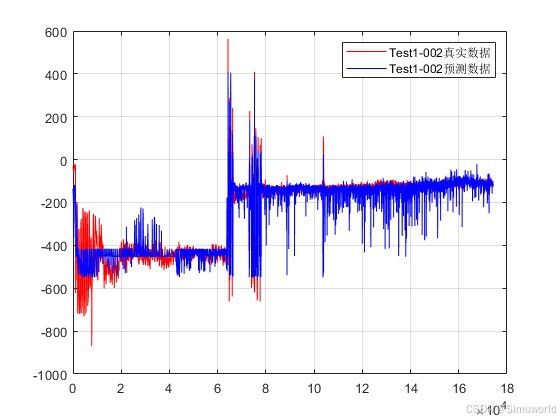
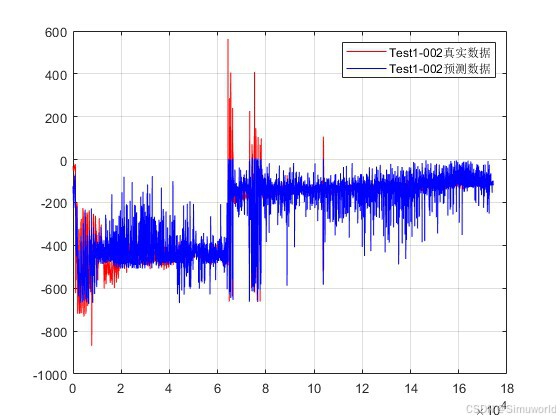
plot(Ker*T1,'r');
hold on
plot(Ker*T1pre,'b');
grid on
legend('Test1-002真实数据','Test1-002预测数据');
%进行BP神经网络预测
T2pre = sim(net1,P2');
figure;
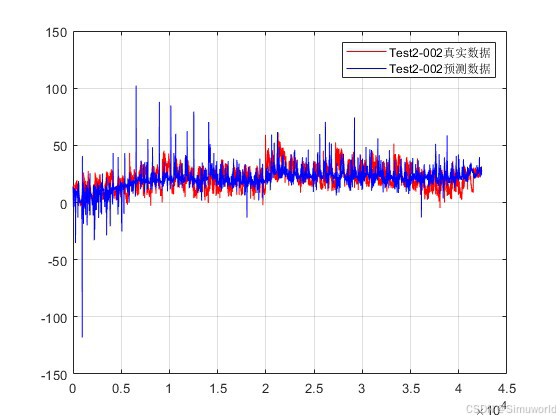
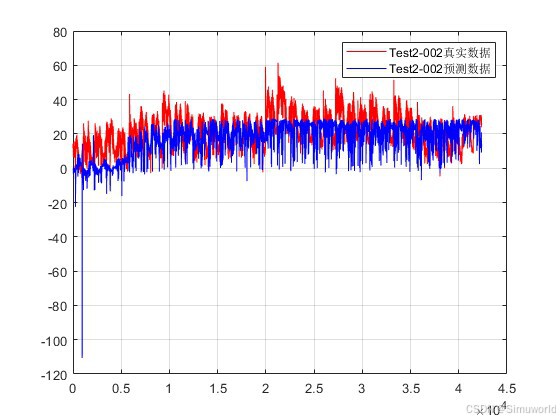
plot(Ker*T2,'r');
hold on
plot(Ker*T2pre,'b');
grid on
legend('Test2-002真实数据','Test2-002预测数据');
%进行BP神经网络预测
T6pre = sim(net1,P6');
figure;
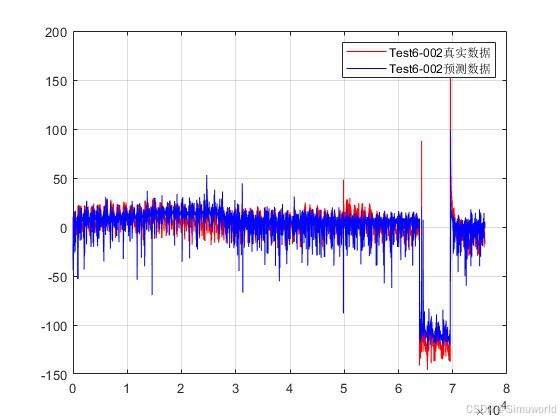
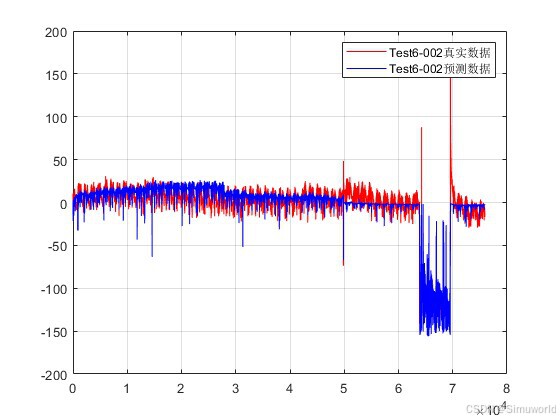
plot(Ker*T6,'r');
hold on
plot(Ker*T6pre,'b');
grid on
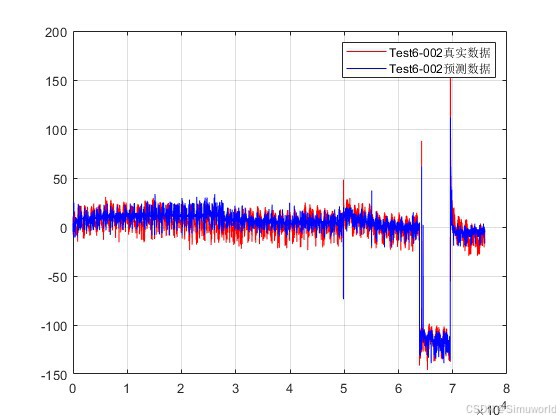
legend('Test6-002真实数据','Test6-002预测数据');
%计算训练误差
disp('预测误差%');
Err1 = abs(100*mean((Ker*T1-Ker*T1pre')./(Ker*T1)))
Err2 = abs(100*mean((Ker*T2-Ker*T2pre')./(Ker*T2)))
Err3 = abs(100*mean((Ker*T6-Ker*T6pre')./(Ker*T6)))3.算法概述
数据挖掘中,神经网络作为一种强大的非线性模型,被广泛应用于模式识别、分类、回归等任务。其中,GRNN(广义回归神经网络)、RBF(径向基函数神经网络)和BP(反向传播神经网络)是三种常见的神经网络模型,它们各自具有不同的特点和适用场景。
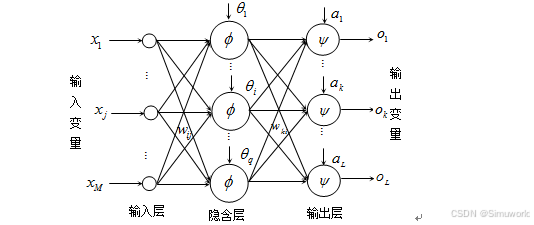
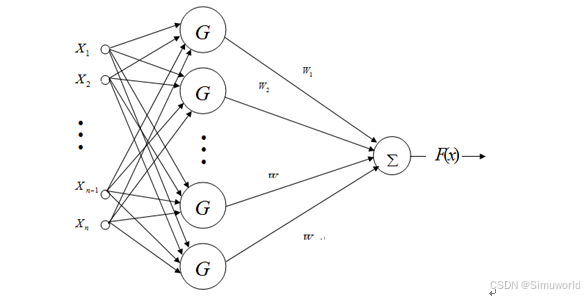
BP神经网络,即Back Propagation神经网络,其本质是一种基于误差反馈传播的神经网络算法。从结构上讲,BP神经网络是由一个信息的正向传播网络和一个误差的反向传播网络两个模块构成。BP神经网络的基本结构如下图所示:
C从图2的结构可知,BP神经网络主要由输入层,隐含层以及输出层构成。来自外界的信息通过输入层传输进入到隐含层进行处理,并由输出层输出处理结果。当BP神经网络的输出结果和其期望结果之间的误差较大的时候,则进入反向传播阶段,并进行进行审计网络权值的修正,直到输出结果和期望结果误差满足一定条件为止。
RBF网络是一种三层前向网络:
第一层为输入层,由信号源节点组成。
第二层为隐含层,隐单元的变换函数是一种局部分布的非负非线性函数,他对中心点径向对称且衰减。隐含层的单元数由所描述问题的需要确定。
第三层为输出层,网络的输出是隐单元输出的线性加权。
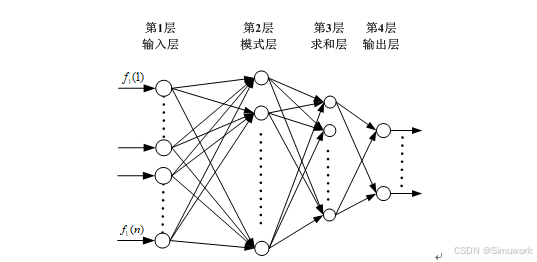
GRNN,即General Regression Neural Network,中文全称为广义回归神经网络,是由The Lockheed Palo Alto研究实验室在1991年提出的。GRNN是一种新型的基于非线性回归理论的神经网络模型。GRNN是建立在非参数核回归基础之上的,该神经网络是以测试样本为后验条件,并从观测样本中计算得到自变量和因变量之间的概率密度函数,然后在计算出因变量关于自变量的回归值。由于GRNN不需要规定模型的类型,只需要设置神经网络的光滑因子参数,GRNN神经网络的光滑因子参数的取值对神经网络的输出影响较大,当光滑因子参数较大的时候,其对应的神经元所覆盖的输入区域就越大;当光滑因子参数较小的时候,神经网络对应的径向基函数曲线较陡,因此神经网络输出结果更接近期望值,但此时光滑度越差。
三种网络对比如下:
- 学习速度:GRNN最快,几乎瞬间完成;RBF次之,因为它只需要确定隐层参数;BP最慢,需要多次迭代。
- 非线性表达能力:BP由于其多层结构,通常具有最强的非线性表达能力;RBF通过径向基函数也能很好地处理非线性问题;GRNN在一定程度上牺牲了非线性表达以换取速度。
- 适用场景:GRNN适用于快速预测和对实时性要求高的场合;RBF适用于需要快速构建模型且对非线性有一定要求的任务;BP则更适合处理复杂、高度非线性的分类和回归问题,尤其是在有足够的计算资源和训练时间的情况下。
4.部分参考文献
[1]杜爱玲,武敬.神经网络在股市预测中的应用——基于BP,RBF与GRNN[J].经营管理者, 2014(11X):1.DOI:CNKI:SUN:GLZJ.0.2014-11-351.
[2]杜爱玲,武敬.神经网络在股市预测中的应用——基于BP,RBF与GRNN[J].经营管理者, 2014(11X):1.DOI:CNKI:SUN:GLZJ.0.2014-11-351.
[3]钱光兴,崔东文.RBF与GRNN神经网络模型在城市需水预测中的应用[J].水资源与水工程学报, 2012(5):5.DOI:CNKI:SUN:XBSZ.0.2012-05-038.
5.程序内容,运行方法和源码获取
5.1 程序包括
matlab程序,训练测试样本以及三种网络模型的理论公式
5.2 运行方法
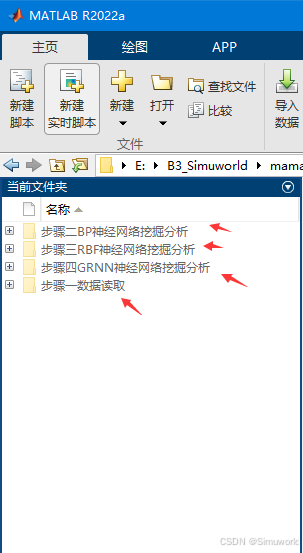
1.在matlab的左侧的当前文件夹窗口;
2.按标题步骤1,步骤2,步骤3,步骤4,以此运行。
5.3 源码获取
step1.打开博客主页的左侧推广栏查看,或扫博客文章底部信息
step2.然后用电脑打开网页链接,输入文章标题搜索