前言:
总结一下数理统计中的基本概念,一些用python的实现在这里。不断持续更新。
1. 几个基本概念
1.1 次序统计量
1.2 样本偏度与样本峰度
1.3 经验分布函数
1.4 抽样分布
2. 统计中的常用分布
2.1 卡方分布
2.2 t 分布
2.3 F分布
3. 指数型分布族(和广义线性模型有关)
4. 点估计
4.1 极大似然估计
5. 区间估计
5.1 几个基本概念
6. 假设检验——显著性检验
6.1 几个基本概念
6.2 求取某假设的显著性检验的步骤
6.3 似然比检验
6.4 p值
1. 几个基本概念:
1.1 次序统计量:
设
X
1
,
X
2
,
⋯
,
X
n
X_1, X_2, \cdots , X_n
X1,X2,⋯,Xn为样本,把
X
1
,
X
2
,
…
,
X
n
X_1, X_2, …, X_n
X1,X2,…,Xn由小到大排列成
X
(
1
)
≤
⋯
≤
X
(
n
)
X_{(1)}\le\cdots\le X_{(n)}
X(1)≤⋯≤X(n),则称
(
X
(
1
)
,
⋯
,
X
(
n
)
)
(X_{(1)}, \cdots, X_{(n)})
(X(1),⋯,X(n))为次序统计量,
X
(
i
)
X_{(i)}
X(i)则成为第
i
i
i个次序统计量。
-
样本 p p p分位数:对于给定的 p ∈ ( 0 , 1 ) p \in (0, 1) p∈(0,1),我们称: m n , p = X ( [ n p ] ) + ( n + 1 ) ( p − [ n p ] n + 1 ) ( X ( [ n p ] + 1 ) − X ( [ n p ] ) ) (1) m_n,_p=X_{([np])}+(n+1)(p-\frac{[np]}{n+1})(X_{([np]+1)}-X_{([np])}) \tag1 mn,p=X([np])+(n+1)(p−n+1[np])(X([np]+1)−X([np]))(1)为此样本的 p p p分位数. 特别的,样本中位数定义为: X m e d = { X ( n + 1 2 ) n 为 奇 数 X ( n 2 ) + X ( n 2 + 1 ) 2 n 为 偶 数 (2) X_{med} =\begin{cases}X_{(\frac{n+1}{2})}&n为奇数\\\\\frac{X_{(\frac{n}{2})}+X_{(\frac{n}{2}+1)}}{2}&n为偶数\end{cases}\tag2 Xmed=⎩⎪⎨⎪⎧X(2n+1)2X(2n)+X(2n+1)n为奇数n为偶数(2)
-
极值统计量:称 X ( 1 ) X_{(1)} X(1)和 X ( n ) X_{(n)} X(n)为极小值和极大值统计量.
-
极差: R = X ( n ) − X ( 1 ) R=X_{(n)}-X_{(1)} R=X(n)−X(1)
1.2 样本偏度与样本峰度:
- 样本偏度: n ∑ i = 1 n ( X i − X ˉ ) 3 [ ∑ i = 1 n ( X i − X ˉ ) 2 ] 3 2 \frac{\sqrt{n}\sum\limits_{i=1}^n(X_i-\bar{X})^3}{[\sum\limits_{i=1}^n(X_i-\bar{X})^2]^{\frac{3}{2}}} [i=1∑n(Xi−Xˉ)2]23ni=1∑n(Xi−Xˉ)3,可以用来度量随机变量概率分布的不对称性。大于0时,概率分布图右偏;小于0时,概率分布图左偏。
- 样本峰度: n ∑ i = 1 n ( X i − X ˉ ) 4 [ ∑ i = 1 n ( X i − X ˉ ) 2 ] 2 − 3 \frac{n\sum\limits_{i=1}^n(X_i-\bar{X})^4}{[\sum\limits^n_{i=1}(X_i-\bar{X})^2]^2}-3 [i=1∑n(Xi−Xˉ)2]2ni=1∑n(Xi−Xˉ)4−3,用来度量随机变量概率分布的陡峭程度。峰度值越大,概率分布图越高尖,峰度值越小,越矮胖。
- 详见偏态分布学习笔记(期望,中位数,众数)
1.3 经验分布函数:
设 X 1 , ⋯ , X n X_1, \cdots, X_n X1,⋯,Xn为取自总体的分布函数为 F ( x ) F(x) F(x)的样本, X ( 1 ) ≤ ⋯ ≤ X ( n ) X_{(1)}\le\cdots\le X_{(n)} X(1)≤⋯≤X(n)为其次序统计量,则称: F n ( x ) = 1 n ∑ i = 1 n I { X i < x } = { 0 x ≤ X ( 1 ) k n X ( k ) < x ≤ X ( k + 1 ) , k = 1 , ⋯ , n − 1 1 x > X ( n ) (3) F_n(x)=\frac{1}{n}\sum\limits_{i=1}^nI_{\{X_i\lt x\}}=\begin{cases}0 &x\le X_{(1)}\\\frac{k}{n} &X_{(k)}\lt x\le X_{(k+1)}, k=1, \cdots , n-1\\1 &x\gt X_{(n)}\end{cases}\tag3 Fn(x)=n1i=1∑nI{Xi<x}=⎩⎪⎨⎪⎧0nk1x≤X(1)X(k)<x≤X(k+1),k=1,⋯,n−1x>X(n)(3)为样本 X 1 , ⋯ , X n X_1, \cdots, X_n X1,⋯,Xn的经验分布函数。
1.4 抽样分布:
统计量是作为随机变量的样本的函数,故它也有概率分布,于是我们称统计量的概率分布为该统计量的抽样分布。
- 一个重要的抽样分布:设 X 1 , ⋯ , X n X_1, \cdots, X_n X1,⋯,Xn为来自 N ( μ , σ 2 ) N(\mu, \sigma^2) N(μ,σ2)的 I I D IID IID样本,则由概率论的知识可知 X ˉ ∼ N ( μ , σ 2 n ) \bar{X}\sim N(\mu, \frac{\sigma^2}{n}) Xˉ∼N(μ,nσ2)
2. 统计中的常用分布:
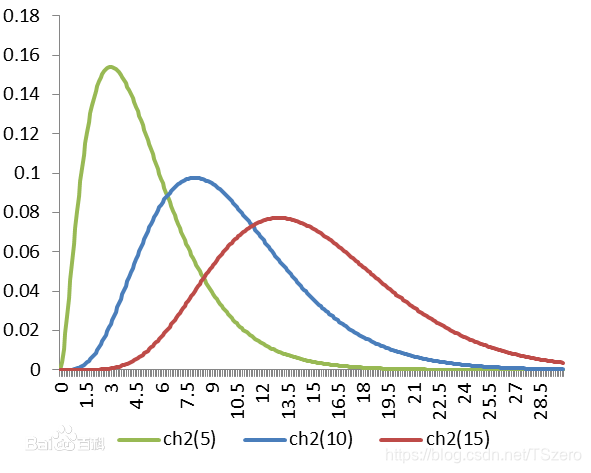
2.1 卡方分布:
设 X 1 , ⋯ , X n ∼ N ( 0 , 1 ) X_1, \cdots, X_n\sim N(0, 1) X1,⋯,Xn∼N(0,1)且是独立同分布的,则称随机变量 ξ = ∑ i = 1 n X i 2 (4) \xi =\sum\limits_{i=1}^nX_i^2\tag4 ξ=i=1∑nXi2(4)所服从的分布为自由度为 n n n的 χ 2 \chi^2 χ2分布,也称 ξ \xi ξ为自由度为 n n n的 χ 2 \chi^2 χ2随机变量,并记为 ξ ∼ χ 2 ( n ) \xi\sim\chi^2(n) ξ∼χ2(n).
- P D F PDF PDF: f ( x ) = { 1 2 n / 2 Γ ( n / 2 ) e − x 2 x n 2 − 1 , x > 0 0 , x ≤ 0 (5) f(x)=\begin{cases}\frac{1}{2^{n/2}\Gamma(n/2)}e^{-\frac{x}{2}}x^{\frac{n}{2}-1}, &x\gt0\\0, &x\le0\end{cases}\tag5 f(x)={2n/2Γ(n/2)1e−2xx2n−1,0,x>0x≤0(5)其中 n n n为自由度。
- 图像:
1.随着 n n n的增大,它的对称性越来越好,峰度越来越小
2.随着 n n n的增大,其图形越来越像正态分布的概率密度函数
3.随着 n n n的增大,它的图形越来越向右移动,且尾部越来越大
- 期望: E ξ = n E\xi=n Eξ=n
- 方差: V a r ξ = 2 n Var \xi=2n Varξ=2n
- 独立可加性:设 ξ ∼ χ 2 ( m ) , η ∼ χ 2 ( n ) \xi\sim\chi^2(m), \eta\sim\chi^2(n) ξ∼χ2(m),η∼χ2(n),且 ξ , η \xi, \eta ξ,η相互独立,则 ξ + η ∼ χ 2 ( m + n ) \xi+\eta\sim\chi^2(m+n) ξ+η∼χ2(m+n)
- ★★ 很重要的一个定理:设 X 1 , ⋯ , X n ∼ N ( μ , σ 2 ) X_1, \cdots, X_n\sim N(\mu, \sigma^2) X1,⋯,Xn∼N(μ,σ2)且是独立同分布的, X ˉ \bar{X} Xˉ和 S n 2 S_n^2 Sn2分别是样本均值和方差,则 X ˉ ∼ N ( μ , σ 2 n ) (6) \bar{X}\sim N(\mu, \frac{\sigma^2}{n})\tag6 Xˉ∼N(μ,nσ2)(6) ( n − 1 ) S n 2 / σ 2 ∼ χ 2 ( n − 1 ) (7) (n-1)S_n^2/\sigma^2\sim\chi^2(n-1)\tag7 (n−1)Sn2/σ2∼χ2(n−1)(7) X ˉ 与 S n 2 独 立 (8) \bar{X}与S_n^2独立\tag8 Xˉ与Sn2独立(8)由 ( 8 ) (8) (8)可知,如果一组随机样本的均值与方差独立,那么总体分布必为正态分布。
证明:
令
A
\bm A
A为如下的正交矩阵:
[
1
n
1
n
1
n
1
n
⋯
1
n
1
n
1
2
−
1
2
0
0
⋯
0
0
1
2
×
3
1
2
×
3
−
2
2
×
3
0
⋯
0
0
⋮
⋮
⋮
⋮
⋮
⋮
⋮
1
(
n
−
1
)
×
n
1
(
n
−
1
)
×
n
1
(
n
−
1
)
×
n
1
(
n
−
1
)
×
n
⋯
1
(
n
−
1
)
×
n
−
n
−
1
(
n
−
1
)
×
n
]
\begin{bmatrix} \frac{1}{\sqrt n} & \frac{1}{\sqrt n} &\frac{1}{\sqrt n} &\frac{1}{\sqrt n} &\cdots &\frac{1}{\sqrt n} &\frac{1}{\sqrt n} \\ \frac{1}{\sqrt 2} & -\frac{1}{\sqrt 2} &0 & 0 & \cdots & 0 & 0\\ \frac{1}{\sqrt {2\times3}} & \frac{1}{\sqrt {2\times3}} &-\frac{2}{\sqrt {2\times3}} & 0 & \cdots & 0 & 0\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \frac{1}{\sqrt {(n-1)\times n}} & \frac{1}{\sqrt {(n-1)\times n}} &\frac{1}{\sqrt {(n-1)\times n}} &\frac{1}{\sqrt {(n-1)\times n}} & \cdots & \frac{1}{\sqrt {(n-1)\times n}} & -\frac{n-1}{\sqrt {(n-1)\times n}}\\ \end{bmatrix}
⎣⎢⎢⎢⎢⎢⎢⎡n1212×31⋮(n−1)×n1n1−212×31⋮(n−1)×n1n10−2×32⋮(n−1)×n1n100⋮(n−1)×n1⋯⋯⋯⋮⋯n100⋮(n−1)×n1n100⋮−(n−1)×nn−1⎦⎥⎥⎥⎥⎥⎥⎤
做如下的正交变换:
[
Y
1
⋮
Y
n
]
=
A
[
X
1
⋮
X
n
]
\begin{bmatrix} Y_1\\ \vdots\\ Y_n \end{bmatrix}=A\begin{bmatrix} X_1\\ \vdots\\ X_n \end{bmatrix}
⎣⎢⎡Y1⋮Yn⎦⎥⎤=A⎣⎢⎡X1⋮Xn⎦⎥⎤
则有:
Y
1
=
1
n
∑
i
=
1
n
X
i
=
n
X
ˉ
Y_1=\frac{1}{\sqrt n}\sum_{i=1}^nX_i=\sqrt n\bar X
Y1=n1i=1∑nXi=nXˉ
∑
i
=
1
n
Y
i
2
=
∑
i
=
1
n
X
i
2
=
∑
i
=
1
n
(
X
i
−
X
ˉ
)
2
+
n
X
ˉ
2
\sum_{i=1}^nY_i^2=\sum_{i=1}^nX_i^2=\sum_{i=1}^n(X_i-\bar X)^2+n\bar X^2
i=1∑nYi2=i=1∑nXi2=i=1∑n(Xi−Xˉ)2+nXˉ2
所以 ( n − 1 ) S n 2 = ∑ i = 1 n ( X i − X ˉ ) 2 = ∑ i = 1 n Y i 2 − n X ˉ 2 = ∑ i = 2 n Y i 2 (n-1)S_n^2=\sum_{i=1}^n(X_i-\bar X)^2=\sum_{i=1}^nY_i^2-n\bar X^2=\sum_{i=2}^nY_i^2 (n−1)Sn2=i=1∑n(Xi−Xˉ)2=i=1∑nYi2−nXˉ2=i=2∑nYi2
而 Y i Y_i Yi是相互独立的正态随机变量,且 E Y 1 = n μ , E Y k = 0 ( k ≥ 2 ) , V a r Y k = σ 2 ( k = 1 ⋯ n ) EY_1=\sqrt n\mu, EY_k=0(k\ge2), Var Y_k=\sigma^2(k=1\cdots n) EY1=nμ,EYk=0(k≥2),VarYk=σ2(k=1⋯n)
所以 Y 1 Y_1 Y1与 ( n − 1 ) S n 2 (n-1)S_n^2 (n−1)Sn2独立,即 X ˉ \bar X Xˉ与 ( n − 1 ) S n 2 (n-1)S_n^2 (n−1)Sn2独立,且 X ˉ ∼ N ( μ , σ 2 n ) , ( n − 1 ) S n 2 / σ 2 ∼ χ 2 ( n − 1 ) \bar{X}\sim N(\mu, \frac{\sigma^2}{n}), (n-1)S_n^2/\sigma^2\sim\chi^2(n-1) Xˉ∼N(μ,nσ2),(n−1)Sn2/σ2∼χ2(n−1)
2.2 t 分布:
设 ξ ∼ N ( 0 , 1 ) , η ∼ χ 2 ( n ) \xi\sim N(0 ,1), \eta\sim\chi^2(n) ξ∼N(0,1),η∼χ2(n),且 ξ , η \xi, \eta ξ,η相互独立,则称随机变量 T = ξ η / n (9) T=\frac{\xi}{\sqrt{\eta/n}}\tag9 T=η/nξ(9)所服从的分布为 t t t分布, n n n为其自由度,且记为 T ∼ t ( n ) T\sim t(n) T∼t(n).
- P D F PDF PDF: f ( x ) = Γ ( ( n + 1 ) / 2 ) n π Γ ( n / 2 ) ( 1 + x 2 / n ) − n + 1 2 (10) f(x)=\frac{\Gamma((n+1)/2)}{\sqrt{n\pi}\Gamma(n/2)}(1+x^2/n)^{-\frac{n+1}{2}}\tag{10} f(x)=nπΓ(n/2)Γ((n+1)/2)(1+x2/n)−2n+1(10)
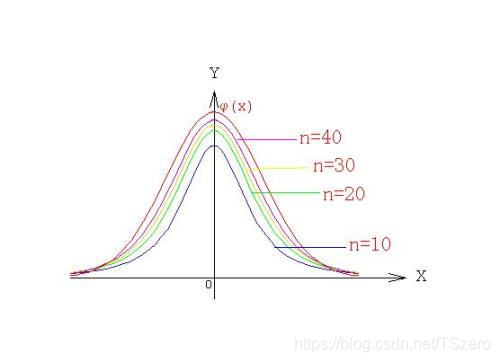
- 图像:
1. t ( n ) t(n) t(n)的PDF关于 y y y轴对称,且 lim ∣ x ∣ → ∞ f ( x ) = 0 \lim\limits_{|x|\to\infty}f(x)=0 ∣x∣→∞limf(x)=0
2.随着 n n n的增大,其峰度越来越高,尾部越来越小
3.当 n n n很大时, t t t分布的PDF接近于标准正态分布的PDF
4.当 n = 1 n=1 n=1时,它是Cauchy分布,故此时期望不存在
- 期望:如果 n > 2 n\gt2 n>2,则 E ξ = 0 E \xi=0 Eξ=0
- 方差: V a r ξ = n n − 2 Var\xi=\frac{n}{n-2} Varξ=n−2n
- ★★ 很重要的一个定理:设 X 1 , ⋯ , X n ∼ N ( μ , σ 2 ) X_1, \cdots, X_n\sim N(\mu, \sigma^2) X1,⋯,Xn∼N(μ,σ2)且独立同分布, X ˉ , S n 2 \bar{X}, S_n^2 Xˉ,Sn2分别是样本均值与方差,则 T = n ( X ˉ − μ ) S n ∼ t ( n − 1 ) (11) T=\frac{\sqrt{n}(\bar{X}-\mu)}{S_n}\sim t(n-1)\tag{11} T=Snn(Xˉ−μ)∼t(n−1)(11)根据此定理,可用样本数据做 t t t检验。
2.3 F 分布:
设 ξ , μ \xi, \mu ξ,μ是自由度分别为 m , n m, n m,n的独立的 χ 2 \chi^2 χ2随机变量,则称随机变量 F = ξ / m η / n (12) F=\frac{\xi/m}{\eta/n}\tag{12} F=η/nξ/m(12)所服从的分布为 F F F分布,其自由度为 ( m , n ) (m, n) (m,n),且记为 F ∼ F ( m , n ) F\sim F(m, n) F∼F(m,n).
1.设 ξ ∼ χ 2 ( m ) , η ∼ χ 2 ( n ) \xi\sim\chi^2(m), \eta\sim\chi^2(n) ξ∼χ2(m),η∼χ2(n),且 ξ \xi ξ与 η \eta η相互独立,则 Y = ξ + η Y=\xi+\eta Y=ξ+η与 Z = ξ / η Z=\xi/\eta Z=ξ/η相互独立
2.设随机变量 X ∼ F ( m , n ) X\sim F(m, n) X∼F(m,n),则 1 X ∼ F ( n , m ) \frac{1}{X}\sim F(n, m) X1∼F(n,m)
-
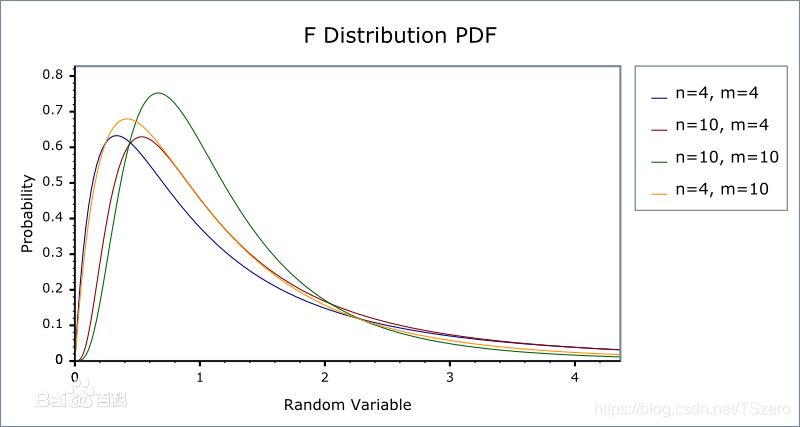
P D F PDF PDF: f ( x ; m , n ) = { 0 , x < 0 Γ ( ( m + n ) / 2 ) Γ ( m / 2 ) Γ ( n / 2 ) ( m n ) ( m x n ) m / 2 − 1 ( 1 + m x n ) − ( m + n ) / 2 , x > 0 (13) f(x;m, n)=\begin{cases}0, &x\lt0 \\ \frac{\Gamma((m+n)/2)}{\Gamma(m/2)\Gamma(n/2)}(\frac{m}{n})(\frac{mx}{n})^{m/2-1}(1+\frac{mx}{n})^{-(m+n)/2}, &x\gt0\end{cases}\tag{13} f(x;m,n)={0,Γ(m/2)Γ(n/2)Γ((m+n)/2)(nm)(nmx)m/2−1(1+nmx)−(m+n)/2,x<0x>0(13)
-
图像:
-
期望: E ξ = n n − 2 , n > 2 E\xi=\frac{n}{n-2}, n\gt2 Eξ=n−2n,n>2
-
方差: V a r ξ = n 2 ( 2 m + 2 n − 4 ) m ( n − 2 ) 2 ( n − 4 ) , n > 4 Var\xi=\frac{n^2(2m+2n-4)}{m(n-2)^2(n-4)}, n\gt4 Varξ=m(n−2)2(n−4)n2(2m+2n−4),n>4
-
★★ 很重要的一个定理:设 X 1 , ⋯ , X m ∼ N ( μ 1 , σ 1 2 ) X_1, \cdots, X_m\sim N(\mu_1, \sigma_1^2) X1,⋯,Xm∼N(μ1,σ12)且独立同分布, Y 1 , ⋯ , Y n ∼ N ( μ 2 , σ 2 2 ) Y_1, \cdots, Y_n\sim N(\mu_2, \sigma_2^2) Y1,⋯,Yn∼N(μ2,σ22)且独立同分布,且两组样本独立,则 F = S 1 m 2 / σ 1 2 S 2 n 2 / σ 2 2 ∼ F ( m − 1 , n − 1 ) (14) F=\frac{S_{1m}^2/\sigma_1^2}{S_{2n}^2/\sigma_2^2}\sim F(m-1, n-1)\tag{14} F=S2n2/σ22S1m2/σ12∼F(m−1,n−1)(14)其中, S 1 m 2 = 1 m − 1 ∑ i = 1 m ( X i − X ˉ ) 2 S_{1m}^2=\frac{1}{m-1}\sum\limits_{i=1}^{m}(X_i-\bar{X})^2 S1m2=m−11i=1∑m(Xi−Xˉ)2, S 2 n 2 = 1 n − 1 ∑ i = 1 n ( Y i − Y ˉ ) 2 S_{2n}^2=\frac{1}{n-1}\sum\limits_{i=1}^{n}(Y_i-\bar{Y})^2 S2n2=n−11i=1∑n(Yi−Yˉ)2,特别的,如果 σ 1 = σ 2 \sigma_1=\sigma_2 σ1=σ2,则 F = S 1 m 2 S 2 n 2 ∼ F ( m − 1 , n − 1 ) F=\frac{S_{1m}^2}{S_{2n}^2}\sim F(m-1, n-1) F=S2n2S1m2∼F(m−1,n−1).
综合 2.2 2.2 2.2和 2.3 2.3 2.3,可有如下定理:
设 X 1 , ⋯ , X m ∼ N ( μ 1 , σ 2 ) X_1, \cdots, X_m\sim N(\mu_1, \sigma^2) X1,⋯,Xm∼N(μ1,σ2)且独立同分布, Y 1 , ⋯ , Y n ∼ N ( μ 2 , σ 2 ) Y_1, \cdots, Y_n\sim N(\mu_2, \sigma^2) Y1,⋯,Yn∼N(μ2,σ2)且独立同分布,且全样本独立,则 T = ( X ˉ − Y ˉ ) − ( μ 1 − μ 2 ) ( m − 1 ) S 1 m 2 + ( n − 1 ) S 2 n 2 m n ( m + n − 2 ) m + n ∼ t ( m + n − 2 ) T=\frac{(\bar X-\bar Y)-(\mu_1-\mu_2)}{\sqrt{(m-1)S^2_{1m}+(n-1)S^2_{2n}}}\sqrt{\frac{mn(m+n-2)}{m+n}}\sim t(m+n-2) T=(m−1)S1m2+(n−1)S2n2(Xˉ−Yˉ)−(μ1−μ2)m+nmn(m+n−2)∼t(m+n−2)
证明:
由 X 1 , ⋯ , X m ∼ N ( μ 1 , σ 2 ) X_1, \cdots, X_m\sim N(\mu_1, \sigma^2) X1,⋯,Xm∼N(μ1,σ2)且独立同分布, Y 1 , ⋯ , Y n ∼ N ( μ 2 , σ 2 ) Y_1, \cdots, Y_n\sim N(\mu_2, \sigma^2) Y1,⋯,Yn∼N(μ2,σ2)且独立同分布,且全样本独立可知, ( m − 1 ) S 1 m 2 + ( n − 1 ) S 2 n 2 σ 2 ∼ χ 2 ( m + n − 2 ) (*) \frac{(m-1)S_{1m}^2+(n-1)S_{2n}^2}{\sigma^2}\sim \chi^2(m+n-2)\tag{*} σ2(m−1)S1m2+(n−1)S2n2∼χ2(m+n−2)(*)
而 X ˉ ∼ N ( μ 1 , 1 m σ 2 ) \bar X\sim N(\mu_1, \frac{1}{m}\sigma^2) Xˉ∼N(μ1,m1σ2), Y ˉ ∼ N ( μ 2 , 1 n σ 2 ) \bar Y\sim N(\mu_2, \frac{1}{n}\sigma^2) Yˉ∼N(μ2,n1σ2),所以 X ˉ − μ 1 ∼ N ( 0 , 1 m σ 2 ) \bar X-\mu_1\sim N(0, \frac{1}{m}\sigma^2) Xˉ−μ1∼N(0,m1σ2) Y ˉ − μ 2 ∼ N ( 0 , 1 n σ 2 ) \bar Y-\mu_2\sim N(0, \frac{1}{n}\sigma^2) Yˉ−μ2∼N(0,n1σ2)
所以 ( X ˉ − μ 1 ) − ( Y ˉ − μ 2 ) = ( X ˉ − Y ˉ ) − ( μ 1 − μ 2 ) ∼ N ( 0 , 1 m σ 2 + 1 n σ 2 ) (\bar X-\mu_1)-(\bar Y-\mu_2)=(\bar X-\bar Y)-(\mu_1-\mu_2)\sim N(0,\frac{1}{m}\sigma^2+\frac{1}{n}\sigma^2) (Xˉ−μ1)−(Yˉ−μ2)=(Xˉ−Yˉ)−(μ1−μ2)∼N(0,m1σ2+n1σ2)
所以 ( X ˉ − Y ˉ ) − ( μ 1 − μ 2 ) 1 m σ 2 + 1 n σ 2 ∼ N ( 0 , 1 ) (**) \frac{(\bar X-\bar Y)-(\mu_1-\mu_2)}{\sqrt{\frac{1}{m}\sigma^2+\frac{1}{n}\sigma^2}}\sim N(0, 1)\tag{**} m1σ2+n1σ2(Xˉ−Yˉ)−(μ1−μ2)∼N(0,1)(**)
结合 ∗ * ∗式和 ∗ ∗ ** ∗∗式即可证明
3. 指数型分布族(和广义线性模型有关)
设 F = { f ( x , θ ) : θ ∈ Θ } \mathcal{F}=\{f(x,\theta):\theta \in \Theta\} F={f(x,θ):θ∈Θ}是某参数分布族,如果 f ( x , θ ) f(x,\theta) f(x,θ)可以表示成 f ( x , θ ) = c ( θ ) e x p ( ∑ i = 1 k c i ( θ ) T i ( x ) ) h ( x ) (15) f(x,\theta)=c(\theta)exp(\sum\limits_{i=1}^{k}{c_i(\theta)T_{i}(x)})h(x)\tag{15} f(x,θ)=c(θ)exp(i=1∑kci(θ)Ti(x))h(x)(15)则称此分布族为指数型分布族,其中 k k k为正整数, c ( θ ) > 0 , h ( x ) > 0 c(\theta)\gt0, h(x)\gt0 c(θ)>0,h(x)>0.
4. 点估计
4.1 极大似然估计:
- 似然函数: L ( θ , x ) = f ( x , θ ) L(\theta, x)=f(x, \theta) L(θ,x)=f(x,θ),其中, f ( x , θ ) f(x, \theta) f(x,θ)是样本的函数, L ( θ , x ) L(\theta, x) L(θ,x)是参数的函数
- 对数似然函数: l ( θ , x ) l(\theta, x) l(θ,x)或 l ( θ ) = l n L ( θ , x ) l(\theta)=ln L(\theta, x) l(θ)=lnL(θ,x)
- 得分函数或似然方程: ∂ l ( θ , x ) ∂ θ j = 0 , j = 1 , ⋯ , k \frac{\partial l(\theta, x)}{\partial \theta_j}=0, j=1,\cdots,k ∂θj∂l(θ,x)=0,j=1,⋯,k,其中, θ ∈ Θ ⊆ R k \theta\in\Theta\subseteq R^k θ∈Θ⊆Rk
- 似然估计的不变原则:如果 g ( θ ) g(\theta) g(θ)是1-1映射,且 θ ^ \hat{\theta} θ^是 θ \theta θ的极大似然估计,则 g ( θ ^ ) g(\hat{\theta}) g(θ^)是 g ( θ ) g(\theta) g(θ)的极大似然估计
5. 区间估计
5.1 几个基本概念:
- 置信区间:设[ θ ^ L ( X ) , θ ^ U ( X ) \hat{\theta}_L(X), \hat{\theta}_U(X) θ^L(X),θ^U(X)]是参数 θ \theta θ的一个区间估计,如果对给定的 α ∈ ( 0 , 1 ) \alpha\in(0, 1) α∈(0,1),有 P θ { θ ^ L ( X ) ≤ θ ≤ θ ^ U ( X ) } ≥ 1 − α , ∀ θ ∈ Θ (16) P_{\theta}\{\hat{\theta}_L(X)\le\theta\le\hat{\theta}_U(X)\}\ge1-\alpha, \forall \theta\in\Theta\tag{16} Pθ{θ^L(X)≤θ≤θ^U(X)}≥1−α,∀θ∈Θ(16)则称[ θ ^ L ( X ) , θ ^ U ( X ) \hat{\theta}_L(X), \hat{\theta}_U(X) θ^L(X),θ^U(X)]为 θ \theta θ的置信水平为 1 − α 1-\alpha 1−α的置信区间
- 置信下限: p { θ ^ L ( X ) ≤ θ } ≥ 1 − α (17) p\{\hat{\theta}_L(X)\le\theta\}\ge1-\alpha\tag{17} p{θ^L(X)≤θ}≥1−α(17)
- 置信上限: p { θ ^ U ( X ) ≥ θ } ≥ 1 − α (18) p\{\hat{\theta}_U(X)\ge\theta\}\ge1-\alpha\tag{18} p{θ^U(X)≥θ}≥1−α(18)
6. 假设检验——显著性检验
6.1 几个基本概念:
- 假设或统计假设:在统计中,我们需要根据样本去推断一个是否“正确”的命题,就称为一个假设或统计假设
- 检验:通过样本对一个假设做出“对”或“不对”的具体判断规则就称为该假设的一个检验
- 第一类错误(拒真):当原假设 H 0 H_0 H0成立,即 θ ∈ Θ 0 \theta\in\Theta_0 θ∈Θ0时,样本却落入了拒绝域 W W W,此时,由样本我们采取了拒绝 H 0 H_0 H0的错误决策,称这样的错误为第一类错误
- 第二类错误(纳伪):当备择假设 H 1 H_1 H1成立,即 θ ∈ Θ 1 \theta\in\Theta_1 θ∈Θ1时,样本却落入了接受域 W ‾ \overline{W} W,此时,由样本我们采取了接受 H 0 H_0 H0的错误决策,称这样的错误为第二类错误
- 显著性水平:对于检验 ψ \psi ψ和事先给定的 α ∈ ( 0 , 1 ) \alpha\in(0,1) α∈(0,1),如果满足 P θ { X ∈ W } ≤ α , ∀ θ ∈ Θ 0 (19) P_{\theta}\{X\in W\}\le \alpha, \forall\theta\in\Theta_0\tag{19} Pθ{X∈W}≤α,∀θ∈Θ0(19)则称 α \alpha α是检验 ψ \psi ψ的显著性水平或水平,也称 ψ \psi ψ为显著性水平 α \alpha α的检验
6.2 求取某假设的显著性检验的步骤:
- 根据实际问题,建立统计假设 H 0 ↔ H 1 H_0\leftrightarrow H_1 H0↔H1;
- 选取一个合适的统计量 T ( X ) T(X) T(X),使当 H 0 H_0 H0成立时, T T T的分布已知,且与参数 θ \theta θ无关(称此分布为统计量 T T T的零分布);
- 根据 H 0 H_0 H0和 H 1 H_1 H1的特点,确定拒绝域 W W W的区间形式;
- 对于给定的显著性水平 α \alpha α,确定拒绝域 W W W;
- 由样本观测值 x x x,计算统计量 T ( X ) T(X) T(X)的值 T ( x ) T(x) T(x),由 T ( x ) T(x) T(x)是否属于 W W W,作出最终判断。
6.3 似然比检验:
- 似然比统计量:设 X 1 , ⋯ , X n X_1, \cdots, X_n X1,⋯,Xn为来自分布族 F = { f ( x , θ ) : θ ∈ Θ } \mathcal F=\{f(x,\theta):\theta\in\Theta\} F={f(x,θ):θ∈Θ}的 I I D IID IID样本,对于感兴趣的假设 H 0 : θ ∈ Θ 0 ↔ H 1 : θ ∈ Θ 1 = Θ − Θ 0 H_0: \theta\in\Theta_0\leftrightarrow H_1:\theta\in\Theta_1=\Theta-\Theta_0 H0:θ∈Θ0↔H1:θ∈Θ1=Θ−Θ0,令 λ ( X ) = s u p θ ∈ Θ 0 f ( X , θ ) s u p θ ∈ Θ f ( X , θ ) (20) \lambda(X)=\frac{sup_{\theta\in\Theta_0}f(X, \theta)}{sup_{\theta\in\Theta}f(X, \theta)}\tag{20} λ(X)=supθ∈Θf(X,θ)supθ∈Θ0f(X,θ)(20)则称统计量 λ ( X ) \lambda(X) λ(X)为假设的似然比,有时也称广义似然比
- 似然比检验(LRT):采用 ( 20 ) (20) (20)作为假设的检验统计量,且取其拒绝域为 { λ ( x ) ≤ c } \{\lambda(x)\le c\} {λ(x)≤c},其中临界值 c c c满足 P θ { λ ( X ) ≤ c } ≤ α , ∀ θ ∈ Θ 0 (21) P_{\theta}\{\lambda(X)\le c\}\le \alpha, \forall \theta \in \Theta_0 \tag{21} Pθ{λ(X)≤c}≤α,∀θ∈Θ0(21)则称此检验为显著性水平 α \alpha α的似然比检验
6.4 p值:
详见:假设检验中p值的理解
参考:《数理统计教程》,王兆军,邹长亮 编著