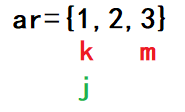目录
一.全排列的定义
1.什么是全排列
从n个不同元素中任取m(m≤n)个元素,按照一定的顺序排列起来,叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。
2.例子
假设现在有一个数组ar如下
ar[3]={1,2,3};那么这个数组的全排列就是
1 2 3
1 3 2
2 1 3
2 3 1
3 2 1
3 1 2 二.code
#include<stdio.h>
void Swap(int& a, int& b)/*交换函数,将a和b的值互换*/
{
int c = a;
a = b;
b = c;
}
void Perm(int* br, int k, int m)/*br代表要进行全排列的数组,k~m代表这个数组中要进行全排列数字的范围*/
{
if (k == m)
{
for (int i = 0; i <= m; ++i)
{
printf("%d ", br[i]);
}
printf("\n");
}
else
{
for (int j = k; j <= m; ++j)
{
Swap(br[j], br[k]);
Perm(br, k + 1, m);
Swap(br[j], br[k]);
}
}
}
int main()
{
int ar[] = { 1,2,3 };
int n = sizeof(ar) / sizeof(ar[0]);
Perm(ar, 0, n - 1);
return 0;
}三.分析
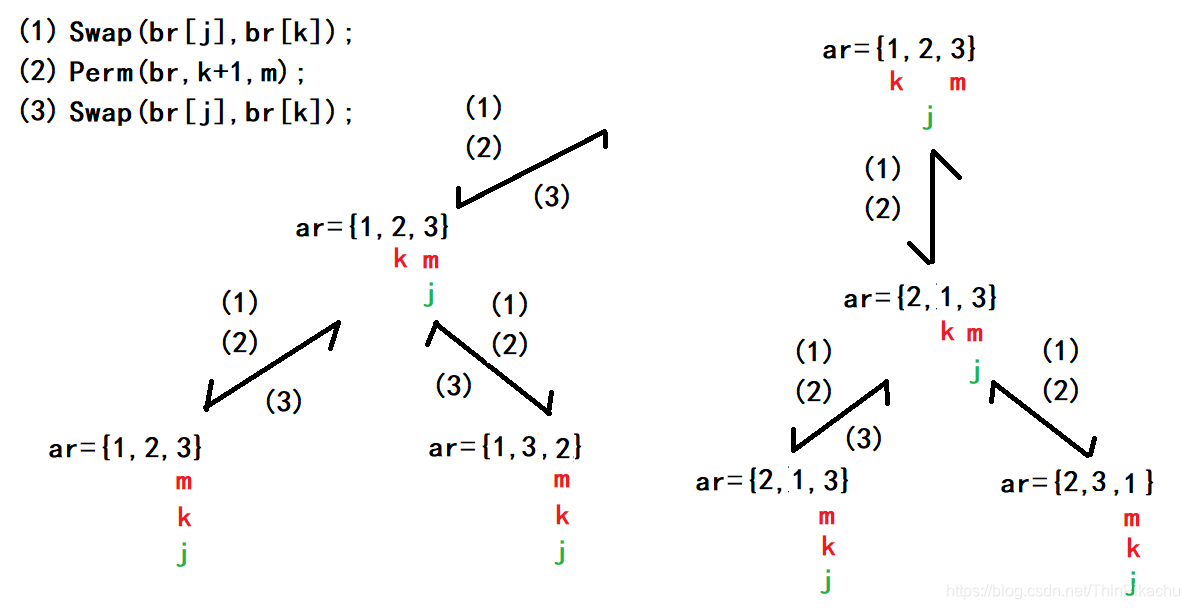
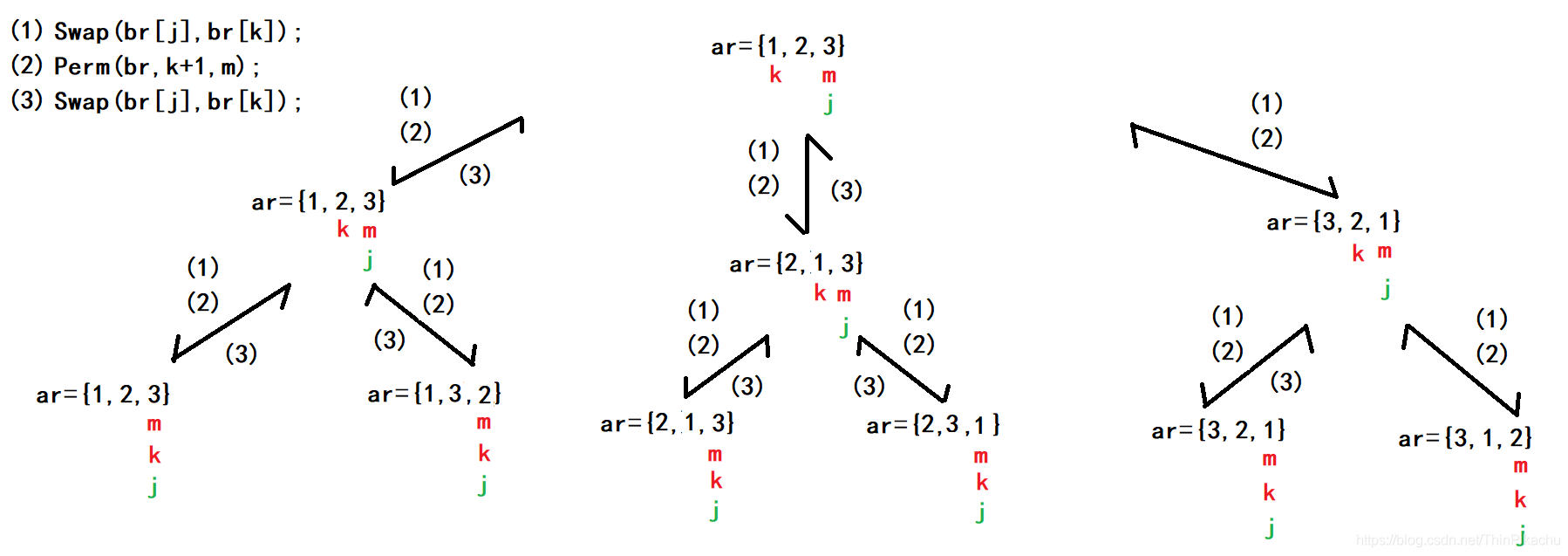
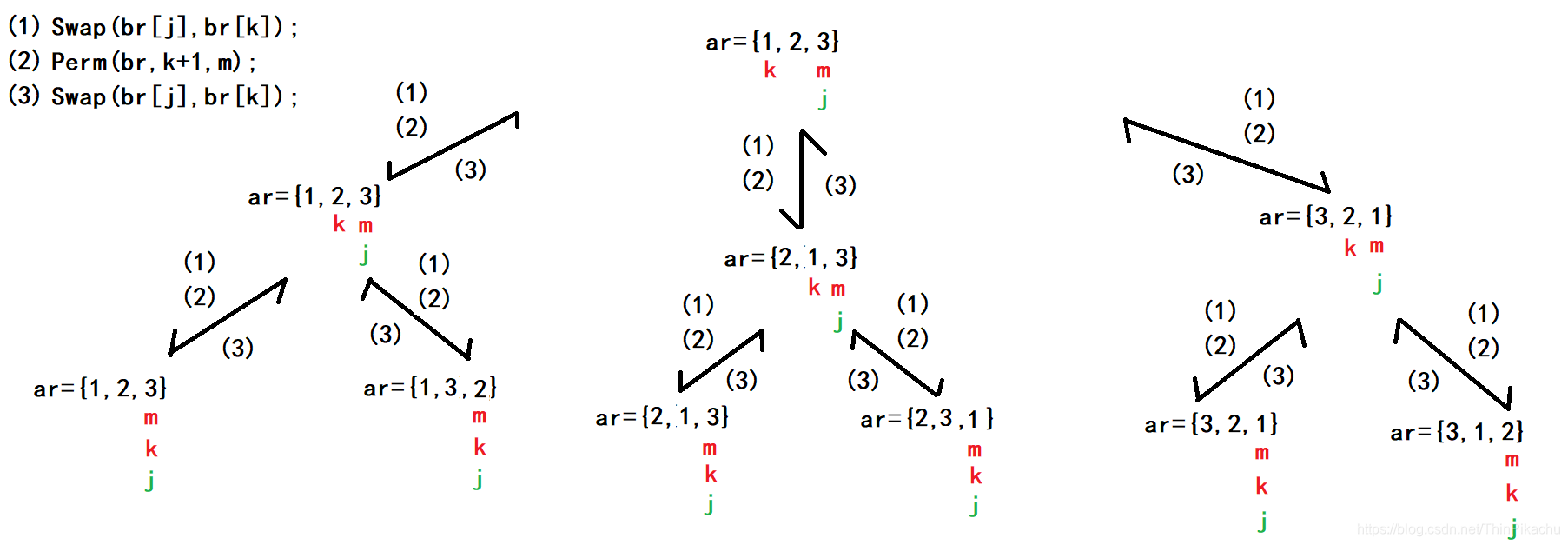
(1)
ar代表要进行全排列的数组,k指向这个数组的开始位置,即0号下标。m指向这个数组的末尾位置,即2号下标。
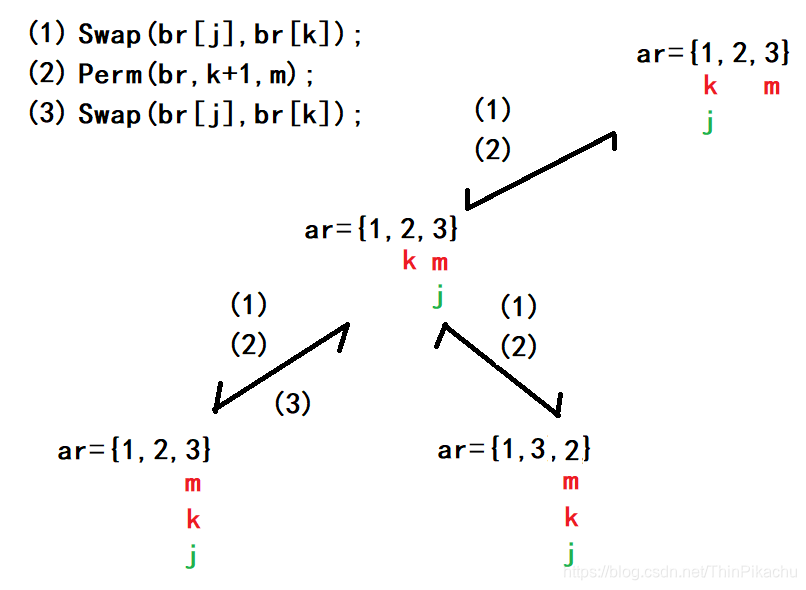
首先进入Perm函数后,先判断k是否等于m,这里k=0,m=2,不相等。接着将k的值赋给j,进入for循环后,首先执行交换函数,将ar[k]和ar[j]的值互换。接着再递归调用Perm函数,这时k的值向后移动一格。
进入新的Perm函数后,k!=m,继续接着将k的值赋给j,进入for循环后,首先执行交换函数,将ar[k]和ar[j]的值互换。接着再递归调用Perm函数,这时k的值向后移动一格。
进入新的Perm函数后,此时k==m,所以执行打印语句,即此时全排列的第一个数据为 1,2,3。
注:
这里的 (1)(2)分表代表执行语句
Swap(br[j], br[k]); Perm(br, k + 1, m);
(2)
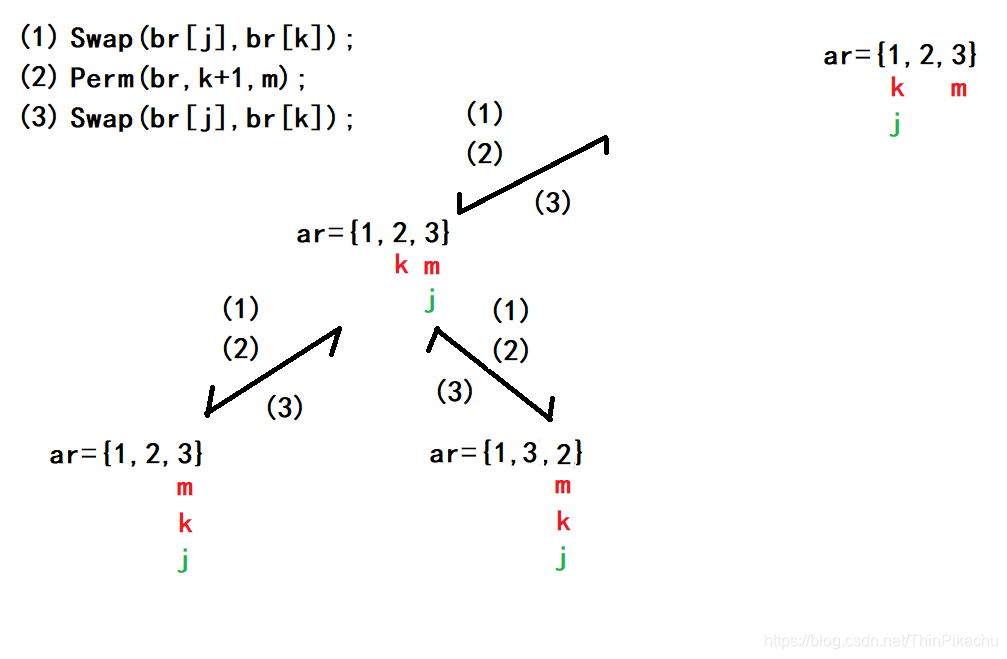
打印完1,2,3后,此时递归函数开始回退,及执行(3)。接着执行for循环中的 j++,此时 j==m。首先执行交换函数,将ar[k]和ar[j]的值互换。接着再递归调用Perm函数,这时k的值向后移动一格。此时k==m,所以执行打印语句,即此时全排列的第二个数据为 1,3,2。
注:
(3)代表执行语句
Swap(br[j], br[k]);执行完这一步后,就让递归函数Perm完成了“归”。
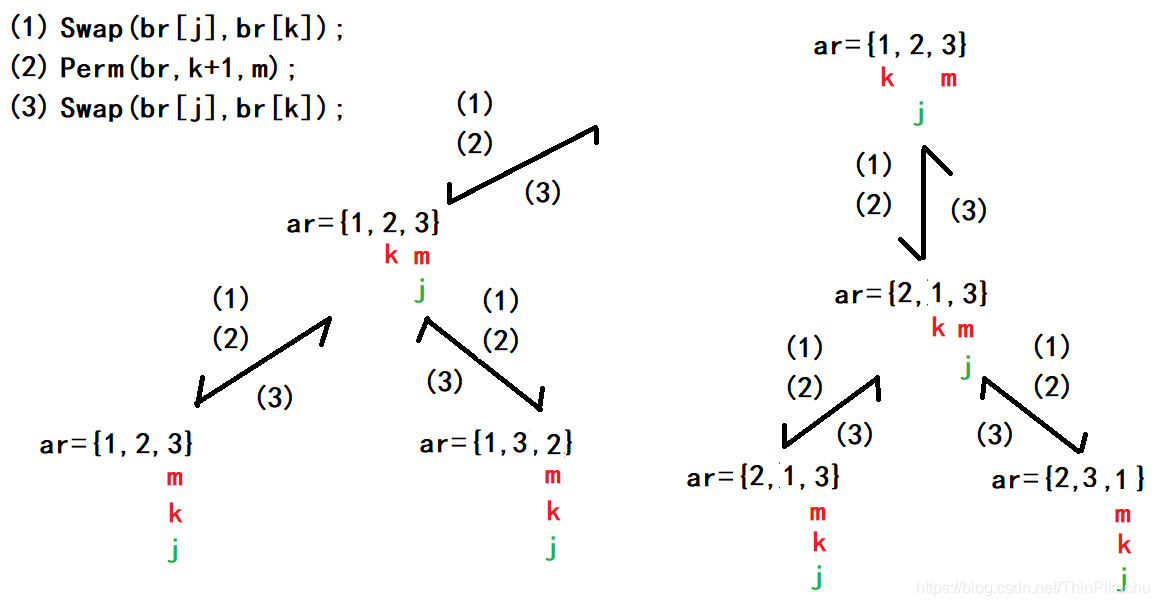
(3)
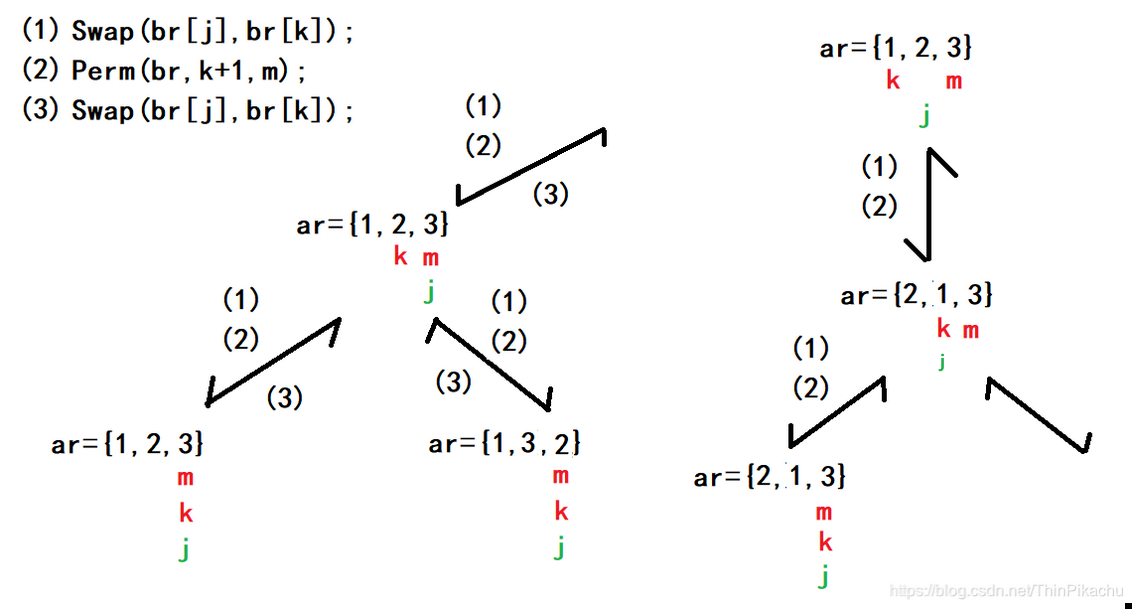
接着从 ar = {1,3,2} 这里开始执行(3),回到ar = {1,2,3}这里。此时 j == m,退出for循环,所以从 ar = {1,2,3} 这里继续执行(3),回退到第一个Perm函数中。
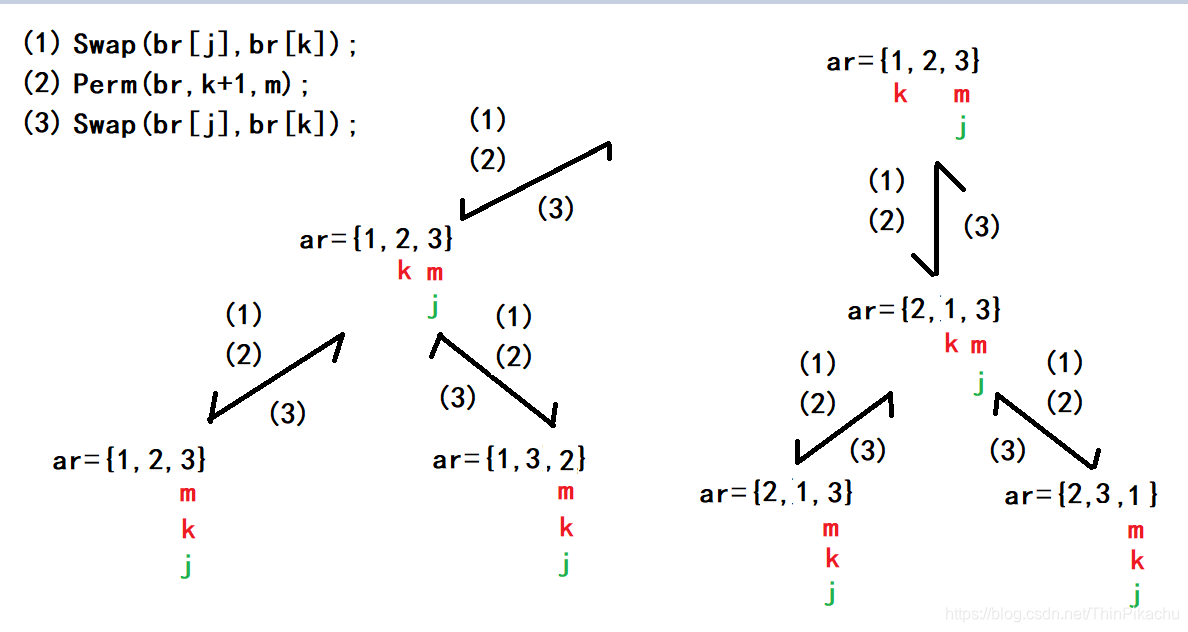
(4)
此时第一个Perm函数中 ar 的 j进行++操作,接着在执行(1)(2),调用了一个新的Perm函数,且此时 ar数组 k位置和j位置的数互换。此时 ar = {2,1,3}。进入Perm函数后,k !=m,进入for循环,将 k的值赋给 j。接着在执行(1)(2)。
执行完(1)(2)后ar = {2,1,3},且此时 k == m,所以执行打印语句,即此时全排列的第三个数据为 2,1,3。
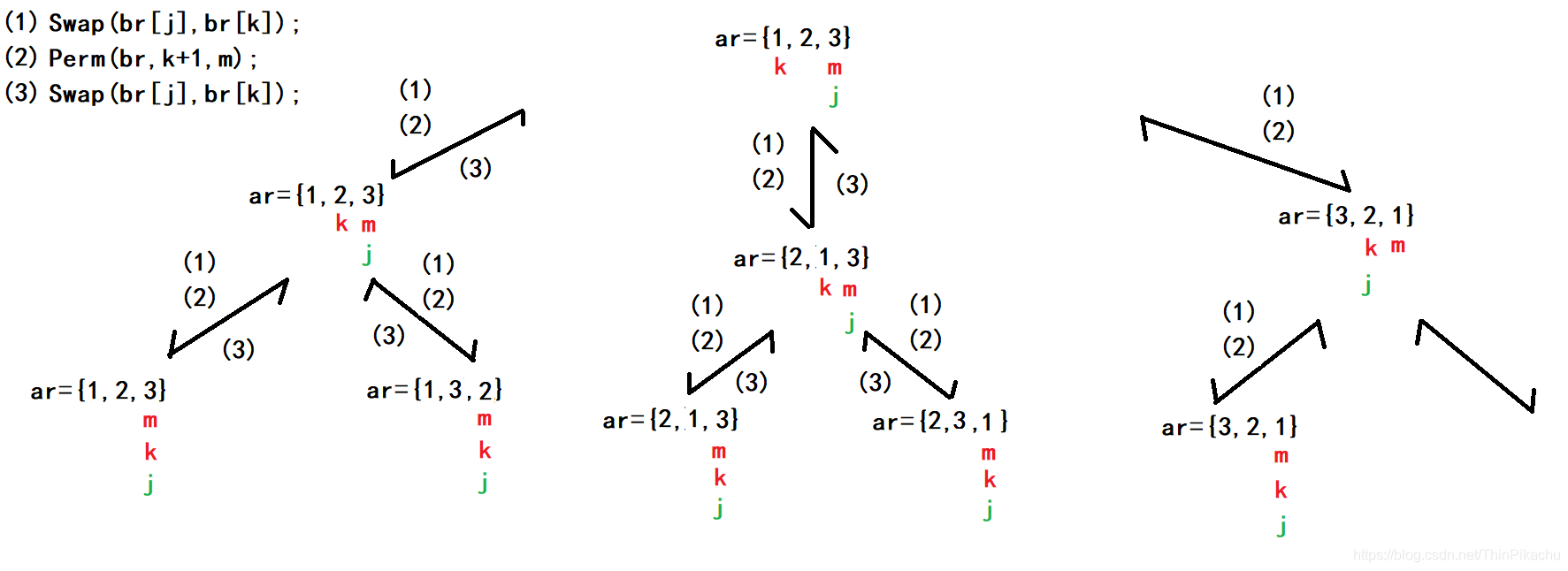
(5)
(6)
(7)
(8)
(9)
(10)