“蓝桥杯”练习系统(基础篇)
一、基础训练
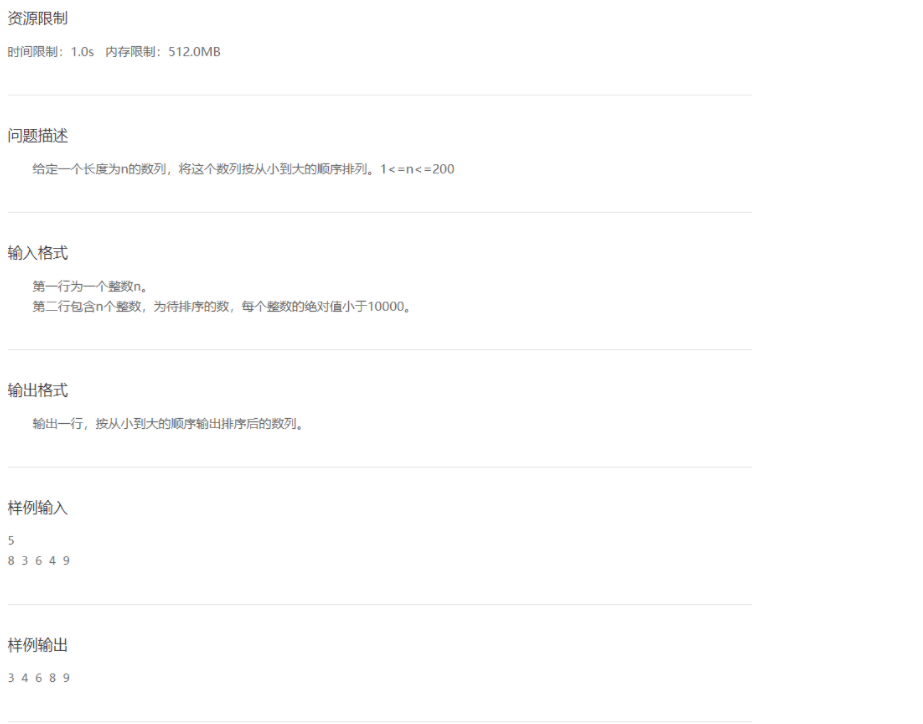
- 数列排序
解法:排序算法-冒泡排序
关键字:数组 排序
函数封装:
#include<bits/stdc++.h>
using namespace std;
void BubbleSort(int a[],int n){
int temp=0;
for(int i=0;i<n-1;i++){
for(int j=0;j<n-1-i;j++){
if(a[j]>a[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
}
int main(){
int n;
cin>>n;
int a[n];
for(int i=0;i<n;i++){
cin>>a[i];
}
BubbleSort(a,n);
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
return 0;
}
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
int a[n];
for(int i=0;i<n;i++){
cin>>a[i];
}
int temp=0;
for(int i=0;i<n-1;i++){
for(int j=0;j<n-1-i;j++){
if(a[j]>a[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
return 0;
}
C++ sort():
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,a[n];
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i];
}
sort(a,a+n);
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
}
时间复杂度:O(n2)
思考过程:
-
一开始想着封装成函数进行计算,想着函数的返回成一个数组回来,查询后
https://www.baidu.com/s?ie=UTF-8&wd=C++%E8%BF%94%E5%9B%9E%E7%B1%BB%E5%9E%8B%E4%B8%BA%E6%95%B0%E7%BB%84
答案:
https://zhidao.baidu.com/question/337749783.html
是没有返回类型为数组类型,详情查看:https://zhidao.baidu.com/question/380269428.html
思路1:但可以这样,参数为int类型数组,返回为vector数组。直接将排序好的数组返回
思路2:C语言存在引用,由于数组是指针,作为参数传递不是复制,而是直接改变本身,所以把函数的返回值设为void,调用函数,数组本身排序,直接在main输出即可
-
排序算法遗忘,看的是Java代码写的冒泡排序(由于n<200,数据量小,可以使用冒泡排序)。
C++与Java的一些对比:
-
https://www.baidu.com/s?ie=utf-8&f=8&rsv_bp=1&tn=baidu&wd=c%E8%AF%AD%E8%A8%80%E8%83%BD%E5%83%8Fjava%E4%B8%80%E6%A0%B7length&oq=c%25E8%25AF%25AD%25E8%25A8%2580%25E6%2580%258E%25E4%25B9%2588%25E5%25BE%2597%25E5%2588%25B0%25E6%2595%25B0%25E7%25BB%2584%25E7%259A%2584%25E9%2595%25BF%25E5%25BA%25A6&rsv_pq=ad4897210006b483&rsv_t=eff3ANdrFh1Th3Aq3I%2B6mHT0edGD8utji4h72oo4vMy3eLHx3YbGjkh0HGI&rqlang=cn&rsv_enter=1&rsv_dl=tb&rsv_sug3=45&rsv_sug1=24&rsv_sug7=100&rsv_sug2=0&rsv_btype=t&inputT=14377&rsv_sug4=15003
在Java中可以直接获得数组的大小(arr.length)
而C++不能这样知道,要么定好固定值数组大小n(所以要cin>>n)
或https://www.jb51.net/article/205038.htm
https://blog.csdn.net/weixin_37536484/article/details/78686028
(一开始想strlen函数求解长度,后来查看后发现是只能求字符串的长度【由于C语言中没有字符串类型,以字符数组作为字符串】https://baike.baidu.com/item/strlen/2737?fr=aladdin;http://c.biancheng.net/c/strlen.html。C++中采用String类型:https://www.cnblogs.com/limera/p/5468551.html)
#define ARRAY_SIZE(x) (sizeof(x)/sizeof((x)[0])) char a[] = { 1,2,3,4 }; length_a = ARRAY_SIZE(a); printf("length of a[]=%d\n", length_a);-
Java的数组可以通过Array直接输出
System.out.println(Arrays.toString(arr));而C++数组只能通过循环遍历输出
为此还专门查了https://blog.csdn.net/weixin_34257076/article/details/92583249
-
-
在写完程序后,想着用函数封装试下,结果太久没有写数组作为函数参数,忘记怎么写;且主函数传递也写错
#include<bits/stdc++.h> using namespace std; void BubbleSort(int a[n]){ //错误点1:因为函数体中有n,写了n //正确写法:int *a(int a[]) int temp=0; for(int i=0;i<n-1;i++){ for(int j=0;j<n-1-i;j++){ if(a[j]>a[j+1]){ temp=a[j]; a[j]=a[j+1]; a[j+1]=temp; } } } } int main(){ int n; cin>>n; int a[n]; for(int i=0;i<n;i++){ cin>>a[i]; } BubbleSort(a[n]); //错误点2:数组传递方式错误 数组直接是引用,不用& for(int i=0;i<n;i++){ cout<<a[i]<<" "; } return 0; }正确写法:
https://www.baidu.com/s?ie=UTF-8&wd=C%E8%AF%AD%E8%A8%80%E6%95%B0%E7%BB%84%E4%BD%9C%E4%B8%BA%E5%8F%82%E6%95%B0
https://blog.csdn.net/weixin_41789607/article/details/80155839
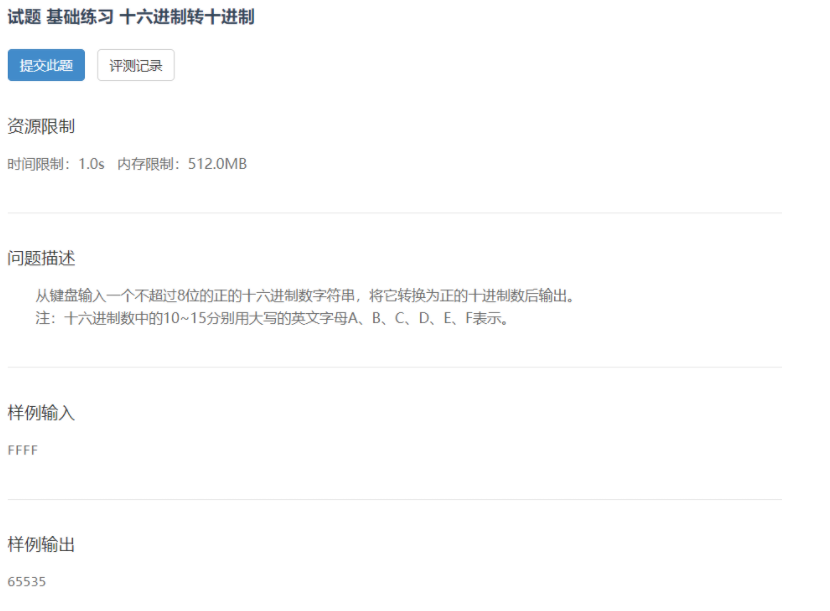
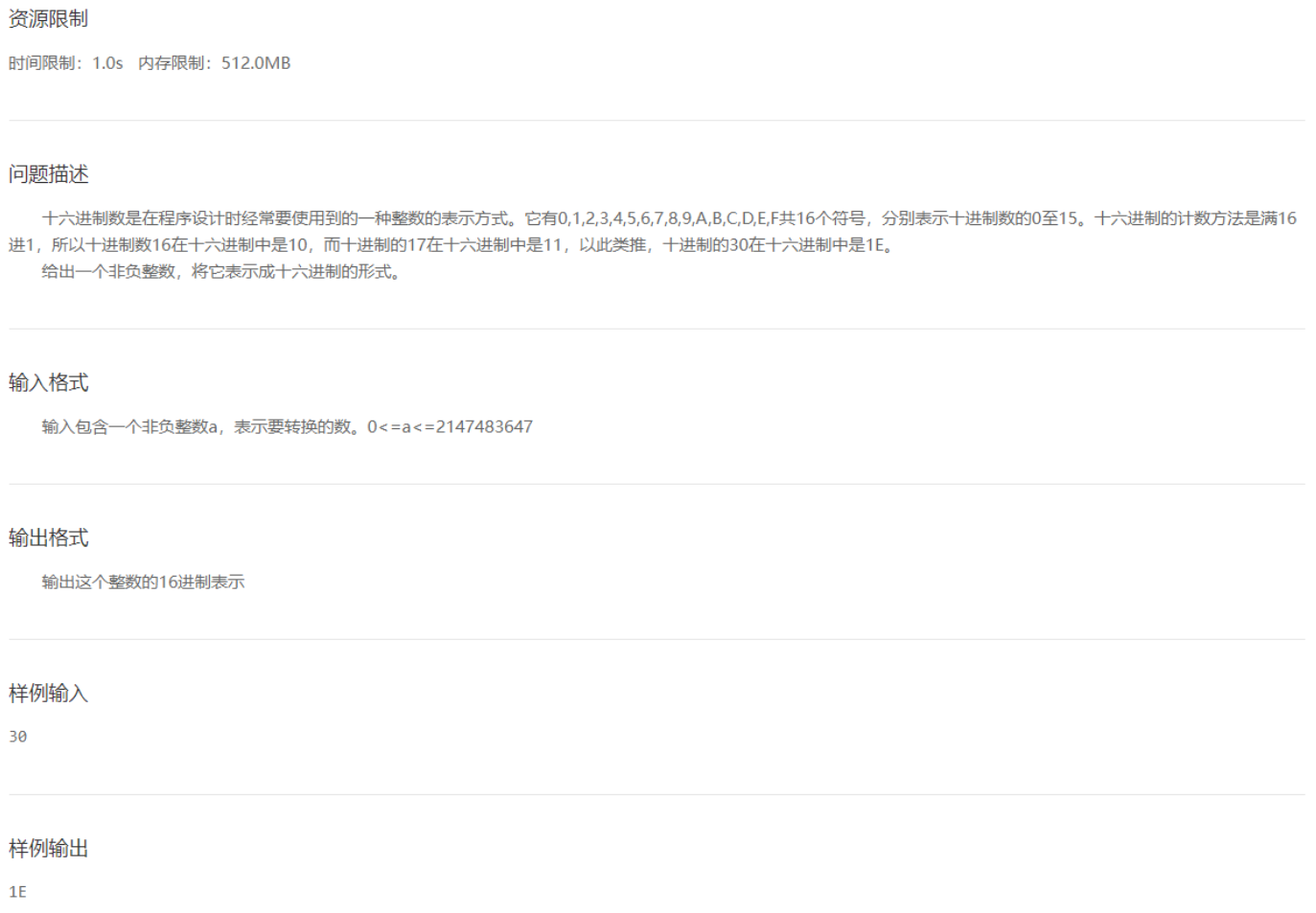
- 十六进制转十进制
解法:枚举 数学规律
关键字:进制转换 字符处理 判断
#include<iostream>
#include<string>
#include<math.h>//下面的pow,需要
using namespace std;
int main()
{
string a;
cin >> a;
char b[16] = { '0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F' };
int c[10];
int k = a.length() - 1;//目的对应好幂的次方
for (int j = 0; j < a.length(); j++)
{
for (int i = 0; i < 16; i++) //b数组大小16
{
if (a[j] == b[i])
{
c[k--] = i;//因为string类型接收的时候,高次在数组低位(例如:string a=“FAB”, a[0]=F,a[1]=A,a[2]=B),所以将高次存在数组高位,以此变正向
}
}
}
long long int sum = 0;//应对sum的值超了int的范围
for (int i = 0; i < a.length(); i++)
{
sum += c[i] * pow(16, i);//这简化转的过程;pow 16的i次方
}
cout << sum << endl;
return 0;
}
时间复杂度:O(n2)
思考过程:
-
首先复习下有关进制方面的知识:https://www.baidu.com/s?ie=UTF-8&wd=C++%E8%BF%9B%E5%88%B6
https://www.jb51.net/article/83754.htm
http://c.biancheng.net/view/1759.html
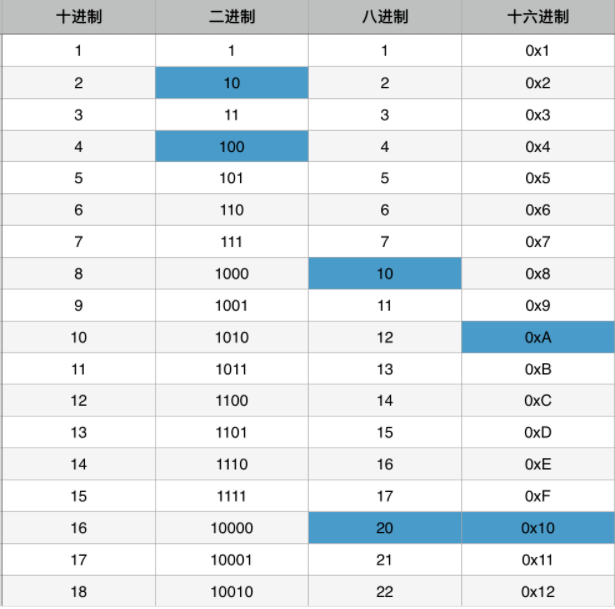
十六进制、八进制不是很熟,比较熟悉的为十进制、二进制
先对输入格式进行分析:要求输入十六进制数(不明白A~F在十六进制代表什么?)
十六进制数的基数是16,采用的数码是0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。其中A-F分别表示十进制数字10-15。
通常,对十六进制数的表示,可以在数字的右下角标注16或H,**但在C语言中是在数的前面加数字0和字母X即0X来表示,以数字“0”加上“x”或“X”开关都是十六进制数。**例如,十进制数12AF在C语言中表示为0X12AF。
例如:0X1A(或0x1A)的十六进制数相当于十进制数的26=16+10(1→16,A→10)
-
解题思路:
http://c.biancheng.net/view/1725.html
《算法笔记》P93,思想正确,代码只能计算纯数值的,有些问题
图解:
-
所使用到的库函数:
pow:https://www.runoob.com/cprogramming/c-function-pow.html
strlen:https://blog.csdn.net/weixin_42427338/article/details/90109813(char array,string都可)
sizeof:https://baike.baidu.com/item/sizeof/6349467?fr=aladdin
-
在C++中引入头文件#include(引入string类)可以定义string类型的字符串,而C语言中只有字符数组来代替字符串(没有类的概念)。string类型像Java一样,有str.length()方法,且能够通过下标查询到每个元素(像C语言字符数组一样)。https://blog.csdn.net/weixin_39624071/article/details/117016894
在C语言中,char类型数组有两种常见的赋值方式(https://blog.csdn.net/yjh0628/article/details/5830133)
-
方式一:直接使用字符串赋值
这种方式是将string转换成charater array,末尾有’/0’(string类型结束标识),故sizeof(array)的大小为数组元素+1。建议在定义数组时,不指定数组的大小,直接赋值。
-
方式二:对数组中逐一元素赋值
这种方式在定义数组时,既可以指定数组大小,也可以不指定。
-
-
最后,在来说下两次方案提交结果为75分的分析:
- 方案一:https://blog.csdn.net/weixin_52340203/article/details/114649867?spm=1001.2101.3001.6650.7&utm_medium=distribute.pc_relevant.none-task-blog-2defaultBlogCommendFromBaiduRate-7.pc_relevant_antiscan&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2defaultBlogCommendFromBaiduRate-7.pc_relevant_antiscan&utm_relevant_index=11
#include<bits/stdc++.h> using namespace std; int main() { // char S[] = "0123456789ABCDEF"; char S[] ={ '0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F' }; char sixteen[8]; cin>>sixteen; int ten=0; int j = 1; long long int len = strlen(sixteen); for (int i = 0;i < len;i++) { int a; if (sixteen[len - 1 - i] >= '0' && sixteen[len - 1 - i] <= '9') { a = sixteen[len - 1 - i] - '0'; } else { for (int j = 0;j < 16;j++) { if (sixteen[len - 1 - i] == S[j]) { a = j; } } } ten = ten + a * j; j = j * 16; } cout<<ten; }查看了这篇https://codeleading.com/article/89375374672/后,自己测试后,确实FFFFFFFF最大的情况返回值为-1,计算不了
猜测:https://codeleading.com/article/89375374672/
- 方案二:后面看到一篇Java版的https://blog.csdn.net/wnamej/article/details/105587896
一开始看到string转char array很迷惑,认为string都可以用下标取元素,为什么还要转char
查找到C++的string转char array的方法:https://www.cnblogs.com/Pillar/p/4206452.html
#include<bits/stdc++.h> using namespace std; int main(){ string str; cin>>str; int len=str.length(); // for(int i=0;i<len;i++){ // cout<<str[i]; // } // cout<<endl<<len; long a[len]; long sum=0L; for(int i = len-1; i >= 0; i--){ //定义十六进制的权位 long sixteen = 1; for(int j = 1; j < len-i; j++){ sixteen *= 16; } //判断十六进制中的字符是否是字母 if(str[i] >= 'A' && str[i] <= 'Z'){ a[i] = str[i]-55; sum += a[i]*sixteen; }else{ a[i] = str[i]-48; sum += a[i]*sixteen; } } cout<<sum<<endl; return 0; }总结:按照博客的分析,猜想两个方面,一、数据太大,long long放不下。二、可能是涉及ASCII表相关方面换算有问题
对于第一点,可以查看欧拉计划笔记16题,利用数组存数值,改进。
-
十进制转十六进制
解法:枚举 数学规律
关键字:循环 整除 求余 判断
#include<bits/stdc++.h> using namespace std; int main(){ int ten; cin>>ten; if(ten==0) { cout<<'0'<<endl; return 0; } string s="0123456789ABCDEF"; string sixteen=""; int i; while(ten>0){ i=ten%16; sixteen+=s[i]; ten=ten/16; } //倒序输出 for(int j=sixteen.length();j>0;j--){ cout<<sixteen[j-1]; //因为length()比真实下标 } cout<<endl; return 0; }时间复杂度:O(n2)
思考过程:
图解:
- 十六进制转八进制
解法:枚举 数学规律
关键字:进制转换 字符 循环
时间复杂度:O(n2)
思考过程:
- 注意下题目的要点
- 每个十六进制数长度不超过100000
- 输入与输出的十六进制数与八进制数不会有前导0
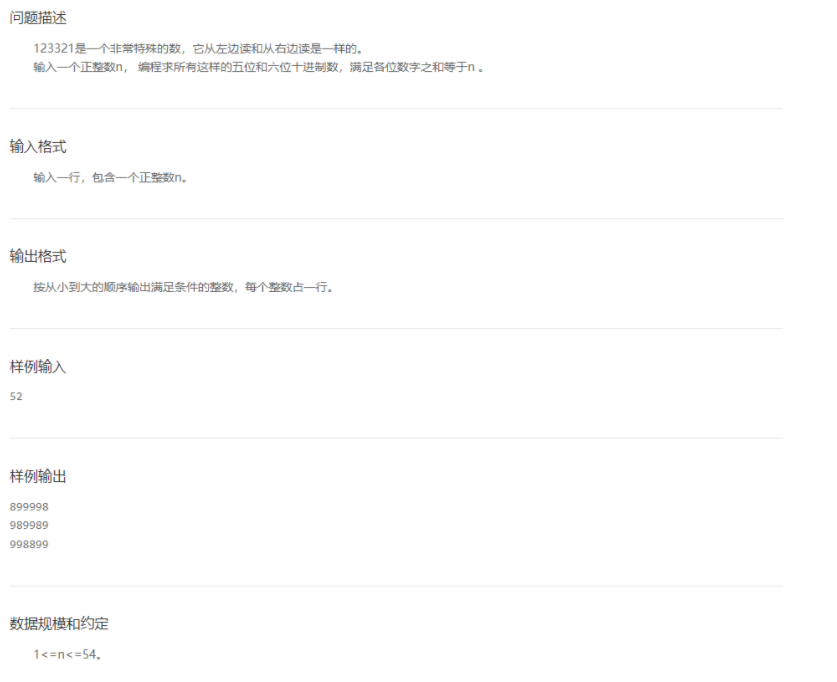
- 特殊回文数
解法:枚举
关键字:回文数 循环 条件语句
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
//五位数的回文数
for(int i=1;i<=9;i++){
for(int j=0;j<=9;j++){
if((i+j)*2<=n&&(i+j)*2>=n-9){ //保证第三个数在0-9之间
cout<<i<<j<<(n-i-i-j-j)<<j<<i<<endl;
}
}
}
//六位数的回文数
for(int k=1;k<=9;k++){
for(int m=0;m<=9;m++){
for(int g=0;g<=9;g++){
if(k+k+m+m+g+g==n){
cout<<k<<m<<g<<g<<m<<k<<endl;;
}
}
}
}
}
时间复杂度:O(n3)
思考过程:
-
注意下题目的要点
- 求所有的五位与六位十进制数
- 隐含条件:数字的首尾不能为0
-
启发:
对于回文数,时刻铭记尽可能使用较小的循环实现枚举
无论对于5位的回文数还是6位的回文数,利用这样的思想:因为每个数会出现两次,利用尽可能少的变量实现对剩余数的表示,以实现较小循环的实现。
-
收获:
循环次数较少的,能够写到三重循环以上
- 回文数
解法:枚举
关键字:循环 判断 回文数
#include<bits/stdc++.h>
using namespace std;
int main(){
for(int i=1;i<=9;i++){
for(int j=0;j<=9;j++){
cout<<(i*pow(10,3)+j*pow(10,2)+j*pow(10,1)+i*pow(10,0))<<endl;
}
}
}
时间复杂度:O(n2)
思考过程:
这道题同样是利用回文数每次出现两个,结合十进制数值转化实现
- 特殊的数字
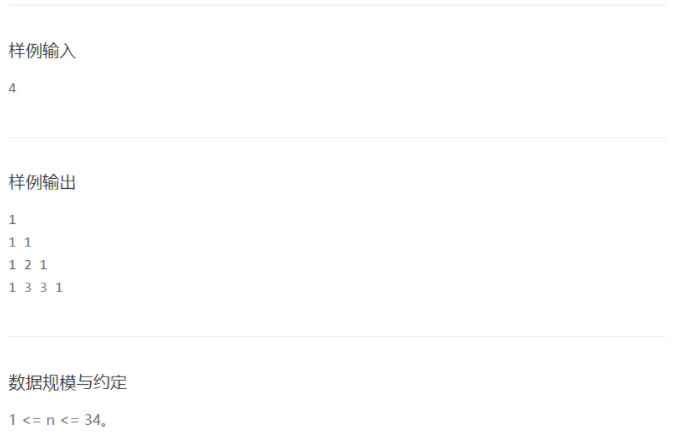
- 杨辉三角形
解法:枚举
关键字:基础练习 二维数组
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
int a[n][n];
for(int i=0;i<n;i++){
a[i][0] = a[i][i] =1;
}
for(int i=2;i<n;i++){
for(int j=1;j<i;j++){
a[i][j] = a[i-1][j]+a[i-1][j-1];
}
}
for(int i=0;i<n;i++){
for(int j=0;j<=i;j++){
cout<<a[i][j]<<" ";
}
cout<<endl;
}
return 0;
}
时间复杂度:O(n2)
思考过程:
首先找到杨辉三角的特征及规律
https://www.cnblogs.com/clover-toeic/p/3766001.html
https://blog.csdn.net/qq_32489573/article/details/101164998
https://www.baidu.com/s?ie=UTF-8&wd=0%EF%BC%81%E7%AD%89%E4%BA%8E
- 查找整数
解法:查找算法—顺序查找
关键字:循环 判断
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
int a[n];
//一行连续输入就不能用循环
for(int i=0;i<n;i++){ //一行输入(因为有空格)或竖列输入都行
cin>>a[i];
//cout<<a[i];
}
int search;
cin>>search;
bool find =true;
//cout<<search;
for(int i=0;i<n;i++){
if(a[i]==search){
//cout<<"a[i]:"<<a[i]<<endl;
find=false;
cout<<i+1<<endl;
break;
}
}
if(find){
cout<<-1<<endl;
}
return 0;
}
时间复杂度:O(n2)
思考过程:
-
首先要具备七大查找算法的知识:https://blog.csdn.net/yimixgg/article/details/88900038
该题由于数据不复杂,直接使用顺序查找即可
-
由于之前没有注意题目条件,未查找到的返回-1,使得测试结果为20
#include<bits/stdc++.h> using namespace std; int main(){ int n; cin>>n; int a[n]; for(int i=0;i<n;i++){ //一行输入或竖列输入都行 cin>>a[i]; //cout<<a[i]; } int search; cin>>search; //cout<<search; for(int i=0;i<n;i++){ if(a[i]==search){ //cout<<"a[i]:"<<a[i]<<endl; cout<<i+1; break; }else{ cout<<-1; break; } } return 0; }题解:
巧妙之处:利用bool判断
https://www.cnblogs.com/loveluking/p/6067661.html
- 数列特征
- 字母图形
- 01字串
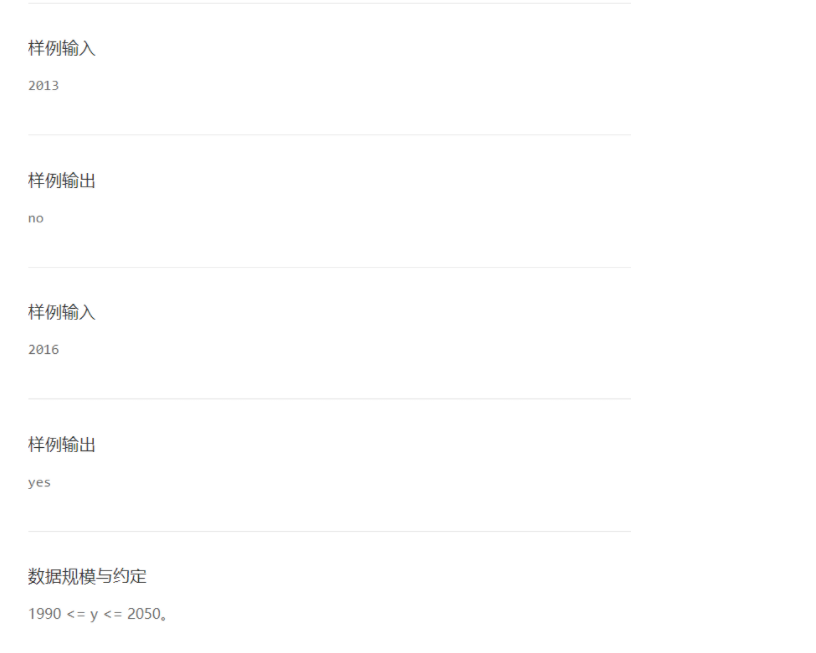
- 闰年判断
解法:枚举
关键字: 条件判断
#include<bits/stdc++.h>
using namespace std;
int main(){
int y;
cin>>y;
while(y!=0){
if(y%4==0&&y%100!=0||y%400==0){ //倍数判断取余,而不是除(除要多重循环)
cout<<"yes";
break;
}else{
cout<<"no";
break;
}
}
return 0;
}
v
时间复杂度:O(n)
思考过程:
判断一个数是不是另一个数的倍数,看这个数循环除另一个数最终结果是不是==0,而取余%就是以上过程的实现。
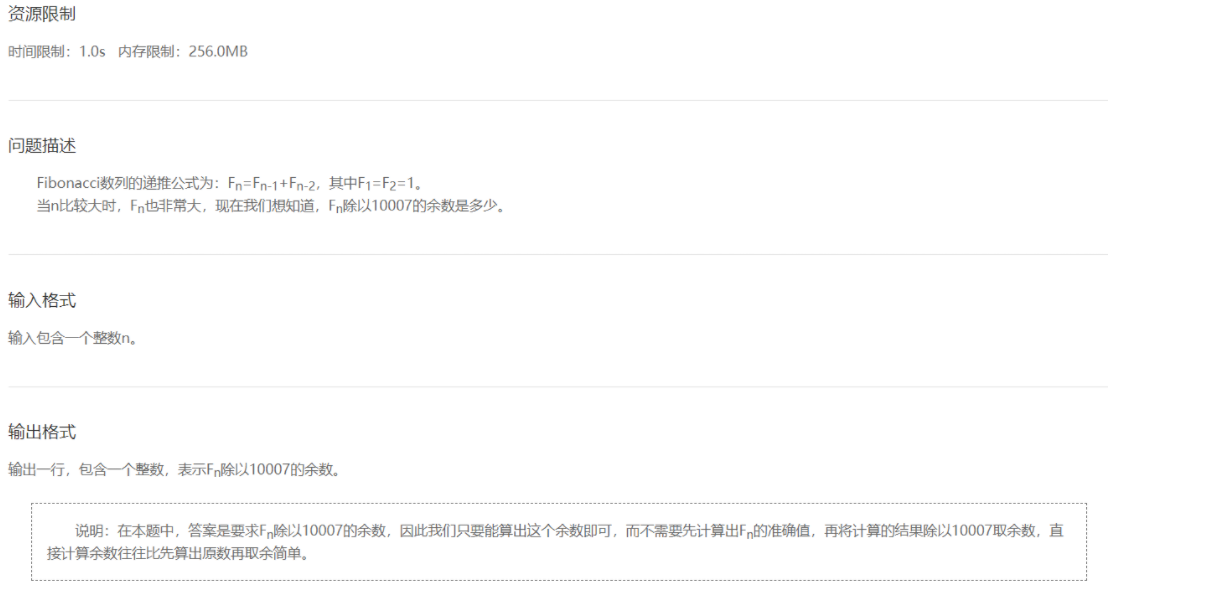
- Fibonacci数列
解法:递推
关键字: 入门 数列 取模
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,f1=1,f2=1,f;
cin>>n;
if(n<=2){
cout<<1;
}else{
for(int i=3;i<=n;i++){
f=(f1+f2)%10007;
f1=f2;
f2=f;
}
cout<<f;
}
return 0;
}
时间复杂度:O(n)
思考过程:
-
注意下题目的要点
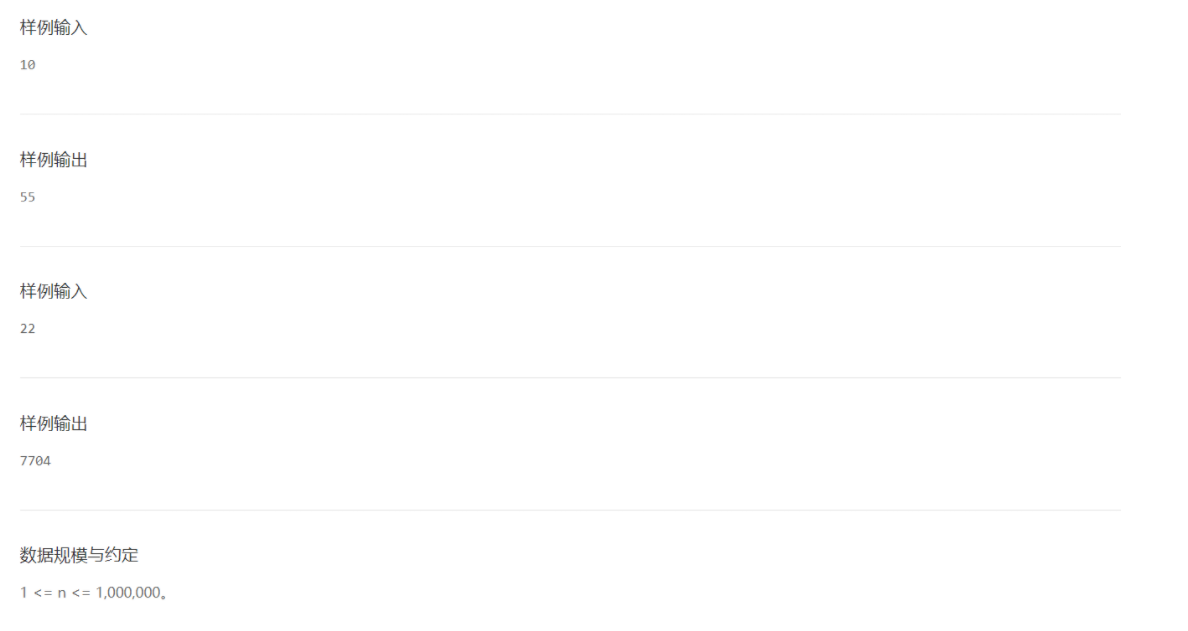
- 不用求出Fn的准确值,只需要求余数
-
常见情况下,我们求解斐波那契数列都是采用“递归“的方式,当由于题目所要求的n太大,递归的方式计算会出现超时,且从F1推导到Fn思路清晰,故采用”递推的方式进行计算。
#include<bits/stdc++.h> using namespace std; int f(int n){ int result; if(n==1||n==2){ result=1; }else#include<bits/stdc++.h> using namespace std; int main(){ int n; cin>>n; int a[n][n]; for(int i=0;i<n;i++){ a[i][0] = a[i][i] =1; } for(int i=2;i<n;i++){ for(int j=1;j<i;j++){ a[i][j] = a[i-1][j]+a[i-1][j-1]; } } for(int i=0;i<n;i++){ for(int j=0;j<=i;j++){ cout<<a[i][j]<<" "; } cout<<endl; } return 0; } result=f(n-1)+f(n-2); } return result; } int main(){ int n; cin>>n; cout<<f(n)%10007; return 0; } -
递推与递归的区别:
https://www.baidu.com/s?ie=utf-8&f=8&rsv_bp=1&tn=baidu&wd=%E9%80%92%E6%8E%A8&oq=%25E9%2580%2592%25E6%258E%25A8%25E5%2592%258C%25E9%2580%2592%25E5%25BD%2592%25E7%259A%2584%25E5%258C%25BA%25E5%2588%25AB&rsv_pq=ef581ad0001cfab9&rsv_t=7fdf6wPuO4Fuj59oE7m%2FsGLqeN5Xl415xY%2FAGtRMXvzMTascGsSJTKUfZ6g&rqlang=cn&rsv_enter=1&rsv_dl=tb&rsv_btype=t&inputT=277&rsv_sug3=7&rsv_sug1=7&rsv_sug7=100&rsv_sug2=0&rsv_sug4=874
https://blog.csdn.net/weixin_44143702/article/details/86551826
https://blog.csdn.net/lybc2019/article/details/104080425
-
接着分析为什么是在每次循环%10007(f=(f1+f2)%10007;),而不是在最后算出Fn在%10007(Fn%10007)。题目已经给我们了提示,因为所定义的int变量可能会超出范围。
#include<bits/stdc++.h> using namespace std; int main(){ int n,f1=1,f2=1,f; cin>>n; if(n<=2){ cout<<1%10007; }else{ for(int i=3;i<=n;i++){ f=f1+f2; f1=f2; f2=f; } } cout<<f%10007; return 0; }很多人可能会想问,为什么每次循环取余数就能够保证最后的结果是正确的?(这样的提问是数据量大,比较抽象的原因造成的)
举例:(自己也没想明白)
假设一开始是1,1%10007的余数还是1本身,所以但数字<10007的时候,每次循环变量f不会因为取余而改变的,故按照提示是能够保证最后的结果正确。
题解:
https://www.cnblogs.com/loveluking/p/6031534.html
https://www.freesion.com/article/20611273335/
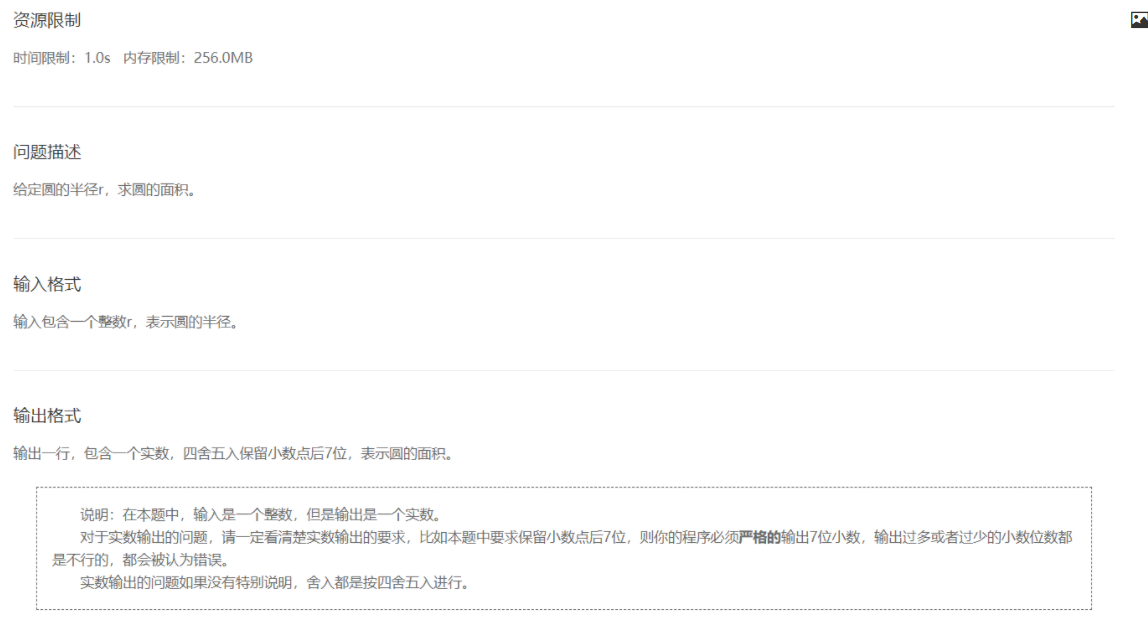
- 圆的面积
解法:数学方法
关键字:入门 实数输出
#include<bits/stdc++.h>
using namespace std;
int main(){
int r;
cin>>r;
double area;
area=r*r*M_PI;
printf("%.7f",area);
return 0;
}
#include<bits/stdc++.h>
using namespace std;
#define PI 3.14159265358979323
int main(){
int r;
cin>>r;
double area;
area=r*r*PI;
printf("%.7f",area);
return 0;
}
时间复杂度:O(1)
思考过程:
-
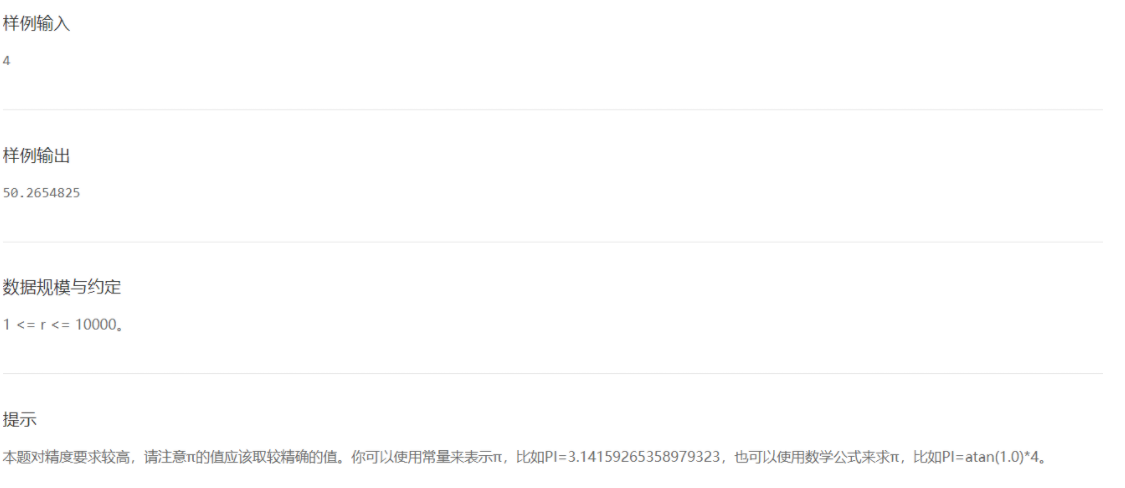
注意下题目的要点:
- 输入的是一个整数,输出的是一个实数 → 涉及类型的转换
- 要求保留七位小数,四舍五入 → C语言在类型转换时是不会四舍五入的
-
收获:
-
在查找相关资料的时候发现,以前我们往往需要自己定义圆周率,C语言的math.h的头文件中提供M_PI宏来表示圆周率
https://blog.csdn.net/qq_40634846/article/details/86618802
https://zhidao.baidu.com/question/564337042.html
-
涉及C语言四舍五入的问题时,C++程序也需要使用C语言的输出方式printf()来控制输出格式
https://blog.csdn.net/whalefall/article/details/80297752
关于保留n位小数的输出形式
https://blog.csdn.net/qq_41113008/article/details/89293673
以及保留n位小数四舍五入问题:
https://www.baidu.com/s?ie=UTF-8&wd=c%E8%AF%AD%E8%A8%80%E6%98%AF%E8%87%AA%E5%8A%A8%E5%9B%9B%E8%88%8D%E4%BA%94%E5%85%A5%E5%90%97
https://zhidao.baidu.com/question/460172887705565805.html
-
-
关于第一次得到10分的分析:
所定义的圆周率长度不够,计算出现问题
因为圆周率不好记忆,建议还是使用头文件math.h下提供的M_PI宏
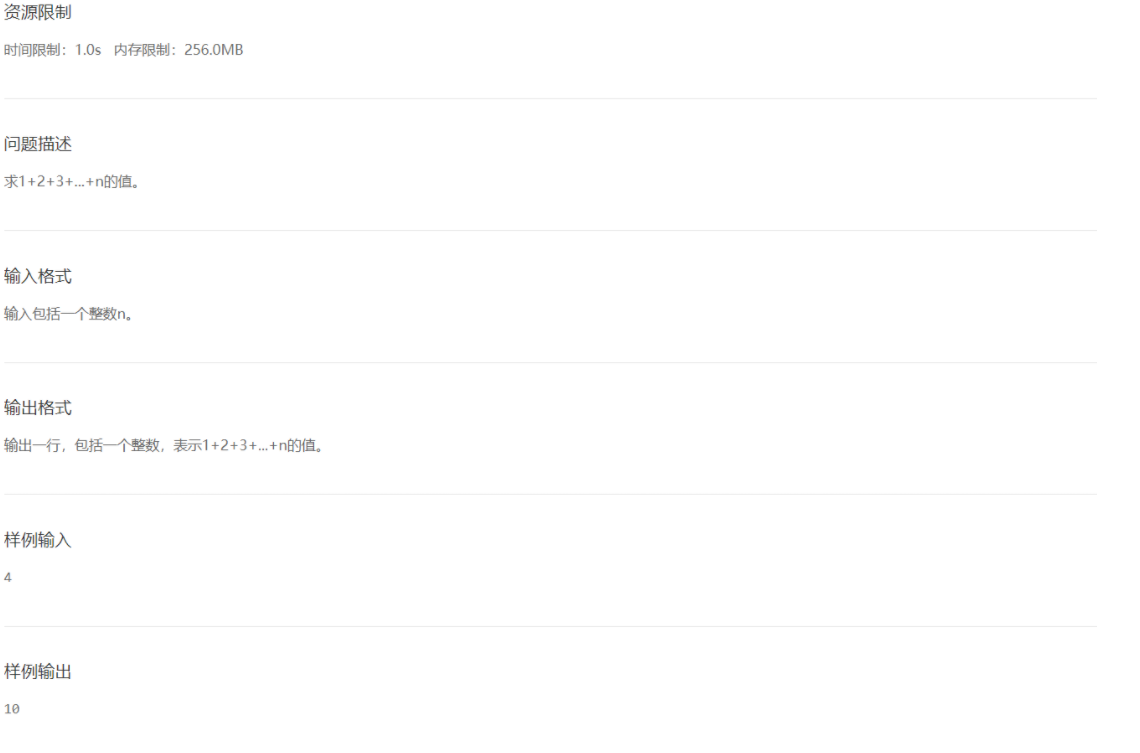
- 序列求和
解法:数学方法—高斯等差数列求和公式/枚举
关键字:入门 求和公式
枚举:
#include<bits/stdc++.h>
using namespace std;
int main(){
long long n,sum=0;
cin>>n;
for(long long i=1;i<=n;i++){
sum+=i;
}
cout<<sum;
return 0;
}
时间复杂度:O(n)
高斯等差数列求和公式:(首项+末项)*项数/2=数列和
#include<bits/stdc++.h>
using namespace std;
int main(){
long long n,sum=0;
cin>>n;
sum=(1+n)*n/2;
cout<<sum;
return 0;
}
时间复杂度:O(1)
看可以看到两者的时间差距还是很明显的
思考过程:
-
注意下题目的要点:
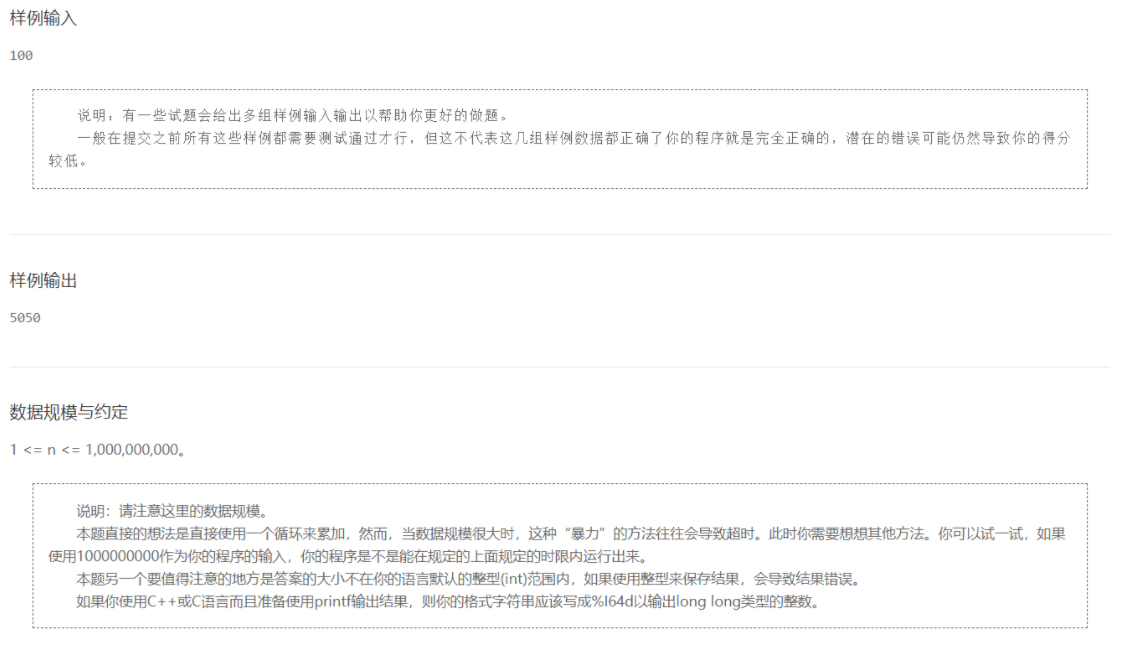
数据规模与约定
1 <= n <= 1,000,000,000(10位)<long long (19位)。
上次遇到这么大规模的数据还是“欧拉计算刷题笔记中16题求2的幂的时候”,在这统一笔记并复习下C/C++的数据基本类型:
https://www.runoob.com/cprogramming/c-data-types.html
https://blog.csdn.net/qq_38410730/article/details/80138714?utm_medium=distribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-1.pc_relevant_paycolumn_v3&spm=1001.2101.3001.4242.2&utm_relevant_index=4
(说明:unsigned int=int,short int =short,long int =long,long long = long long int)
注意:int类型最多能存10位,但最大值位2147483647,不是9999999999(long long同理)
-
因为之前在刷“欧拉计划”16题时有过用数组存高精度数据的经历,因为对这样的做法掌握的不是很透彻,没有搞清楚使用的情形,本以为这道题也要使用相同的思想。采用输入一个char类型的数组(或string类型),转化成int类型计算,但其实这样是矛盾的思想,违背了用数组求高精度基本思想(具体看”欧拉计划“笔记)。
https://www.baidu.com/s?ie=UTF-8&wd=char%E7%B1%BB%E5%9E%8B%E8%BD%AC%E5%8C%96%E4%B8%BAint
https://www.cnblogs.com/daleyzou/p/9510334.html
-
最后,对于输出格式也进行一个总结:
C++使用cout输出不同考虑输出格式,若想使用C的输出方式printf则需要考虑(https://zhidao.baidu.com/question/525357989497186645.html),这也正是题目中所提示的那样
-
幂,阶乘
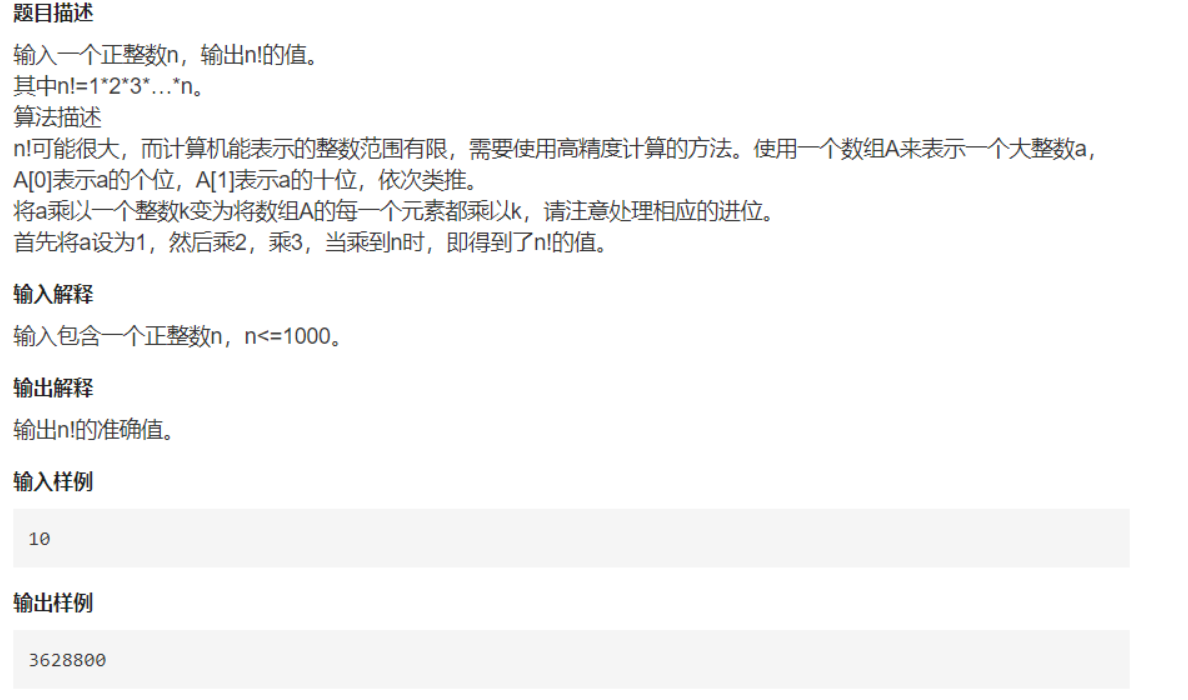
- 阶乘计算
解法:枚举
关键字:高精度
#include<iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int A[10000] = { 0 };//全部初始化为0,防止进行阶乘时出现负数
A[0] = 1;//因为要进行的是乘法,所以第一个数必须为1;
for (int i = 1; i <= n; i++)
{
int carry = 0;//目的,使得上次的相乘与现在无关(如2*3的进位与1*2的无关 )
for (int j = 0; j < 10000; j++)
{
A[j] = A[j] * i + carry;
carry = A[j] / 10;
A[j] = A[j] % 10;
}
}
int end;
for (int i = 10000 - 1; i >= 0; i--)//判断出最后一位的下标,并记录
{
if (A[i] != 0)
{
end = i;
break;
}
}
for (int i = end; i >= 0; i--)
{
cout << A[i];
}
return 0;
}
时间复杂度:O(n2)
思考过程:
-
一开始简单的认为是“欧拉计划的16题”修改语句,str[j]*=2; 变成str[j]*=i;即可,后来调试后发现,因为幂每次乘积不会扩大的量级跟阶乘还是有所不同,无法解决进位的问题。
#include<bits/stdc++.h> using namespace std; int main(){ int str[400]; int i,j,n=0; cin>>n; for(i = 0; i < 400; i++) //初始化 数组a[i]中每一项都为0 { str[i] = 0; } str[0] = 1; for(i = 1; i <= n ;i++) { for(j = 0;j < 400;j++) {//数组的每一个数都乘i str[j]*=i; if(str[j]>0){ cout<<j<<":"<<str[j]<<endl; } } cout<<"~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~"<<endl; for(j = 0;j < 400;j++) {//逢10进1 if(str[j] > 9) { str[j+1]=str[j]/10; cout<<j<<":"<<"2j+1::"<<str[j+1]<<endl; str[j] = str[j] % 10; cout<<j<<":"<<"2j::"<<str[j]<<endl; cout<<"--------------------------------结束"<<endl; // cout<<str[j]<<endl; } } } // for(i = 399;i >= 0;i--){ // cout<<str[i]; // } return 0; } -
图解:
https://blog.csdn.net/weixin_43906799/article/details/104751549
-
若不是高精度问题,求解阶乘问题可以用”递归“的方式进行求解
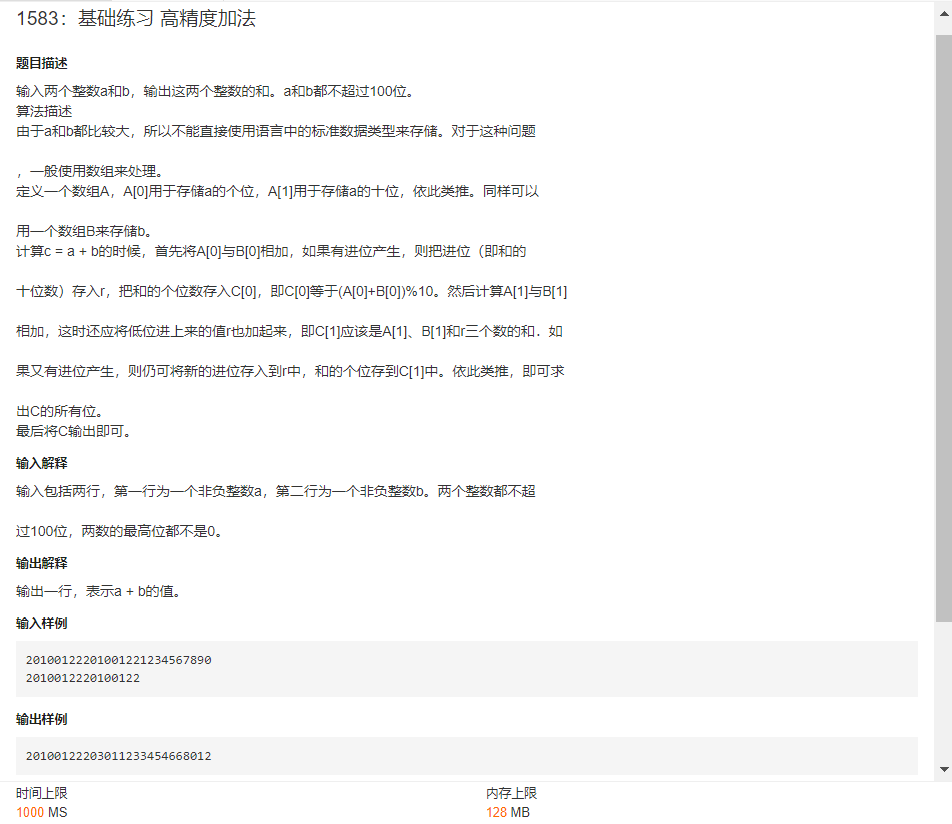
- 高精度加法
解法:数学方法—高斯等差数列求和公式/枚举
关键字:高精度