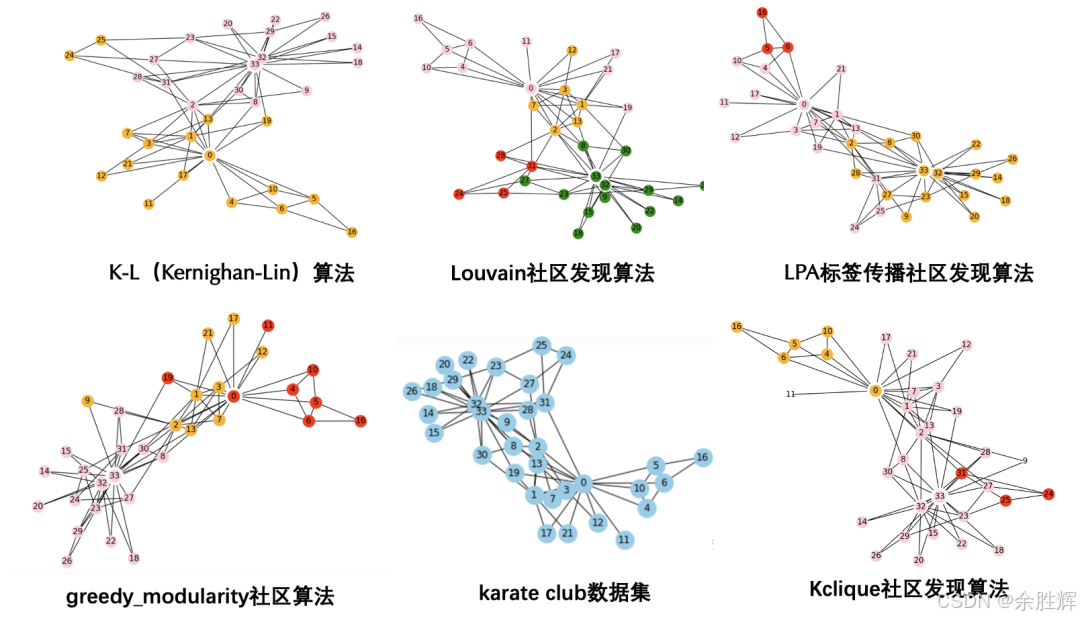
引言
在当今的数字化时代,复杂网络无处不在,从社交网络到生物网络,再到金融网络,这些网络结构复杂且规模庞大。如何从中挖掘出有价值的信息,成为了一个重要的研究课题。社区发现作为复杂网络分析的核心任务,旨在识别网络中紧密连接的节点子集,即社区。Louvain 算法因其高效性和出色的社区划分能力,成为了社区发现领域的热门算法。
本文将带你深入理解 Louvain 算法的原理、实现细节以及如何在实际项目中调优和优化。无论你是初学者还是有一定经验的开发者,都能从中获得实用的知识和技巧。
一、Louvain 算法概述
1.1 什么是 Louvain 算法?
Louvain 算法由比利时学者 Vincent D. Blondel 等人于 2008 年提出,是一种基于模块度优化的社区发现算法。它的目标是通过最大化图的模块度,识别出网络中的社区结构。
模块度(Modularity)是衡量社区划分质量的核心指标,其公式如下:
Q
=
1
2
m
∑
i
,
j
[
A
i
j
−
k
i
k
j
2
m
]
δ
(
c
i
,
c
j
)
Q = \frac{1}{2m} \sum_{i,j} \left[ A_{ij} - \frac{k_i k_j}{2m} \right] \delta(c_i, c_j)
Q=2m1i,j∑[Aij−2mkikj]δ(ci,cj)
其中:
- ( A i j ) ( A_{ij} ) (Aij) 表示节点 ( i ) ( i ) (i) 和节点 ( j ) ( j ) (j) 之间的边权重。
- ( k i ) ( k_i ) (ki) 和 ( k j ) ( k_j ) (kj) 分别表示节点 ( i ) ( i ) (i) 和节点 ( j ) ( j ) (j) 的度。
- ( m ) ( m ) (m) 是图中所有边的权重之和。
- ( δ ( c i , c j ) ) ( \delta(c_i, c_j) ) (δ(ci,cj)) 是指示函数,当节点 ( i ) ( i ) (i) 和节点 ( j ) ( j ) (j) 属于同一社区时为 1,否则为 0。
1.2 Louvain 算法的核心思想
Louvain 算法通过两阶段迭代来优化模块度:
- 节点移动:将每个节点移动到其邻居社区,计算模块度的变化,选择使模块度增益最大的移动。
- 社区合并:将同一社区的节点合并为一个超级节点,重新构建网络,重复上述过程,直到模块度不再增加。
1.3 为什么选择 Louvain 算法?
Louvain 算法的时间复杂度为 ( O ( n log n ) ) ( O(n \log n) ) (O(nlogn)),相比其他社区发现算法(如 Girvan-Newman 算法),它在处理大规模网络时具有显著的优势。此外,Louvain 算法能够处理加权网络、有向网络等多种类型的网络数据。
二、Louvain 算法的详细流程
2.1 初始化阶段
在初始化阶段,Louvain 算法将图中的每个节点视为一个独立的社区。此时,社区的数量与节点数量相同。这一简单而直接的设定为后续的迭代过程奠定了基础,使得算法能够从最细粒度的层面开始探索社区结构。
代码示例:
def initialize_communities(graph):
communities = {node: node for node in graph.nodes()}
return communities
2.2 迭代优化过程
2.2.1 节点移动策略
在每一轮迭代中,算法会遍历所有节点,计算将每个节点移动到其邻居社区时模块度的变化(ΔQ)。如果移动该节点能够增加模块度(ΔQ > 0),则将该节点移动到模块度增益最大的邻居社区。
代码示例:
def move_nodes(graph, communities):
for node in graph.nodes():
best_community = communities[node]
max_delta_q = 0
for neighbor in graph.neighbors(node):
delta_q = calculate_delta_q(graph, communities, node, neighbor)
if delta_q > max_delta_q:
max_delta_q = delta_q
best_community = communities[neighbor]
communities[node] = best_community
return communities
2.2.2 社区合并与更新
当第一轮节点移动结束后,算法将形成的稳定社区视为新的节点,重新构建网络。在此过程中,需重新计算新节点之间的边权重,即将同一社区内的边权重合并为新节点的自环权重,社区间的边权重合并为新节点间的边权重。
代码示例:
def merge_communities(graph, communities):
new_graph = nx.Graph()
community_nodes = {community: set() for community in set(communities.values())}
for node, community in communities.items():
community_nodes[community].add(node)
for community, nodes in community_nodes.items():
new_graph.add_node(community)
for u, v, weight in graph.edges(data='weight'):
community_u = communities[u]
community_v = communities[v]
if community_u == community_v:
if new_graph.has_edge(community_u, community_u):
new_graph[community_u][community_u]['weight'] += weight
else:
new_graph.add_edge(community_u, community_u, weight=weight)
else:
if new_graph.has_edge(community_u, community_v):
new_graph[community_u][community_v]['weight'] += weight
else:
new_graph.add_edge(community_u, community_v, weight=weight)
return new_graph
2.3 收敛条件判定
Louvain 算法的收敛条件是模块度不再增加。在每一轮迭代结束后,算法都会重新计算当前网络的模块度值,并与上一轮迭代结果进行比较。若连续两轮迭代中模块度的变化量小于一个极小的阈值(通常设为接近 0 的值,如 0.0001),或者模块度完全没有增加,即可判定算法已收敛。
代码示例:
def is_converged(old_modularity, new_modularity, threshold=0.0001):
return abs(new_modularity - old_modularity) < threshold
三、Louvain 算法的性能分析
3.1 计算复杂度评估
Louvain 算法的时间复杂度为 ( O ( n log n ) ) ( O(n \log n) ) (O(nlogn)),其中 ( n ) ( n ) (n) 为网络中节点的数量。在每一轮迭代中,算法需要遍历所有节点,计算每个节点移动到相邻社区时模块度的变化,此过程的时间复杂度为 ( O ( n ) ) ( O(n) ) (O(n))。由于算法通常需要进行多轮迭代,且每轮迭代后网络结构会发生变化,节点的社区归属趋于稳定,迭代次数与网络结构相关,一般为 ( O ( log n ) ) ( O(\log n) ) (O(logn)) 量级。综合来看,整体时间复杂度为 ( O ( n log n ) ) ( O(n \log n) ) (O(nlogn))。
与其他一些社区发现算法相比,如传统的穷举法需要考虑所有可能的社区划分组合,其时间复杂度为指数级;Girvan-Newman 算法基于边介数,每次删除边后都要重新计算边介数,时间复杂度较高,在大规模网络中计算成本巨大。而 Louvain 算法通过贪心策略和分层迭代,避免了对所有可能情况的穷举,高效地利用局部最优解逐步逼近全局最优,能够在可接受的时间内处理包含数百万甚至上千万节点的大规模网络,展现出卓越的计算效率。
3.2 收敛性与稳定性探讨
Louvain 算法的收敛性基于模块度不再增加这一条件。在迭代过程中,若连续两轮迭代模块度的变化小于设定的极小阈值(如 0.0001),则判定算法收敛。算法采用贪心策略,在每一步选择使模块度增益最大的节点移动或社区合并操作,这保证了模块度在迭代过程中不会下降,只会上升或保持不变,从而确保最终能够收敛到一个相对稳定的状态。
然而,算法的稳定性受多种因素影响。一方面,网络的动态变化,如节点或边的增删,可能打破已收敛的社区结构,导致模块度下降,需要重新运行算法进行调整。另一方面,初始社区划分也会对结果产生影响,不同的初始划分可能使算法收敛到不同的局部最优解。为增强稳定性,可采用多次随机初始化并选取最优结果的策略,或者结合先验知识确定合理的初始划分,减少随机性带来的差异。此外,在面对动态网络时,可引入增量式更新机制,仅对受变化影响的局部区域重新计算,降低计算成本,维持社区划分的相对稳定。
3.3 与其他算法对比
3.3.1 与 Girvan-Newman 算法比较
Girvan-Newman 算法是一种基于边介数(Edge Betweenness)的层次聚类算法,旨在找到全局最优解。它通过逐步移除图中边介数最大的边,将网络分解为多个连通分量,这些连通分量即为社区。边介数衡量的是一条边在所有节点对最短路径中出现的次数,介数高的边通常位于社区之间,移除它们能够有效分离不同社区。
与 Louvain 算法相比,Girvan-Newman 算法的优势在于能够找到全局最优解,得到的社区结构在理论上更为精确。但其劣势也十分明显,每次移除边后都需重新计算剩余边的介数,时间复杂度高达 ( O(n^3) )(( n ) 为节点数),在大规模网络中计算开销巨大,效率低下。而 Louvain 算法侧重于通过贪心策略快速优化模块度,虽然不能保证全局最优,但能在短时间内得到接近最优的结果,适用于对效率要求较高的大规模网络场景。
3.3.2 在不同场景下的优势对比
在大规模网络场景下,Louvain 算法凭借其低时间复杂度,能够快速完成社区发现任务,如在处理社交网络中的海量用户关系、互联网中的大规模链接结构时,能在短时间内挖掘出有价值的社区信息,为后续分析提供基础。而一些简单的聚类算法,如 K-Means 算法,需要事先指定聚类数量,且在处理高维稀疏网络数据时效果欠佳。
面对动态网络,Louvain 算法可结合增量学习策略,仅对网络变化部分进行局部调整,快速适应节点、边的动态增减,维持社区划分的有效性。相比之下,传统静态算法需重新对整个网络运行算法,耗时较长。
对于加权网络,Louvain 算法能够自然地处理边的权重信息,将权重纳入模块度计算,精准识别出重要连接紧密的社区。部分基于距离的聚类算法,如 DBSCAN 算法,在处理加权边时需复杂的距离转换,易丢失权重蕴含的结构信息。
在存在噪声和数据缺失的网络中,Louvain 算法的贪心策略使其对局部扰动具有一定容忍度,能够稳定地发现主要社区结构。而像标签传播算法等对噪声敏感,少量错误标签可能在传播过程中误导社区划分,导致结果偏差较大。
结语
Louvain 算法作为一种高效的社区发现算法,在社交网络、生物信息学、金融风控等多个领域展现了强大的应用潜力。通过不断优化和改进,Louvain 算法将在未来复杂网络分析中发挥更加重要的作用。
希望本文能帮助你更好地理解 Louvain 算法,并在实际项目中应用它。如果你有任何问题或想法,欢迎在评论区留言讨论!
参考文献
未觉池塘春草梦,阶前梧叶已秋声。

学习是通往智慧高峰的阶梯,努力是成功的基石。
我在求知路上不懈探索,将点滴感悟与收获都记在博客里。
要是我的博客能触动您,盼您 点个赞、留个言,再关注一下。
您的支持是我前进的动力,愿您的点赞为您带来好运,愿您生活常暖、快乐常伴!
希望您常来看看,我是 秋声,与您一同成长。
秋声敬上,期待再会!