Petri Net

In contrast to state machines, state transitions in Petri nets are asynchronous. The ordering of transitions is partly uncoordinated; it is specified by a partial order.

Therefore, Petri nets can be used to model concurrent distributed systems.

Petri Nets: Graphical and Mathematical modeling tools

• graphical tool
• mathematical tool

The graphical presentation of a Petri net is a bipartite graph.

There are two kinds of nodes

• Places: usually model resources or partial state of the system
  Transitions: model state transition and synchronization.
• Arcs are directed and always connect nodes of different types
  Tokens are resources in the places.

Definition of Petri Net

• $C=(P,T,I,O)$

• Places

  $P=p_1,p_2,p_3,\dots ,p_n$

• Transitions

  $T=t_1,t_2,t_3,\dots ,t_n$

• Input 

  I : $T\to P^r$ (r = number of places) $\cdot t$

• Output

  O : $T\to P^q$ (q = number of places) KaTeX parse error: Unexpected character: '
' at position 7: t\cdot
̲


• marking
  µ : assignment of tokens to the places of Petri net $\mu ={\mu }_1,{\mu }_2,{\mu }_3,\dots {\mu }_n$

Petri net consist two types of nodes: places and transitions. And arc exists only from a place to a transition or from a transition to a place.
A place may have zero or more tokens.

Fire

A transition t is called enabled in a certain marking, if:
For every arc from a place p to t, there exists a distinct token in the marking
An enabled transition can fire and result in a new marking
Firing of a transition t in a marking is an atomic operation

Firing a transition results in two things:

• Subtracting one token from the marking of any place p for every arc connecting p to t
• Adding one token to the marking of any place p for every arc connecting t to p

Run-1 Safe PN

A run of a Petri net is a finite or infinite sequence of markings and transitions ${\mu }_0\stackrel{t_0}{\to }{\mu }_1\stackrel{t_1}{\to }\cdots \stackrel{t_{n-1}}{\to }{\mu }_n\stackrel{t_n}{\to }\cdots$ such that ${\mu }_0$ is the initial marking of the net, $t_i\in enabled({\mu }_i)$ for any i (i ≥ 0) , and that ${\mu }_i=({\mu }_{i-1}-\cdot t_{i-1})\cup t_{i-1}\cdot$ for any $i$ ($i\ge 1$).

Properties of Petri Nets

• Sequential Execution
• Synchronization
• Merging
• Fork
• Concurrency
• Conflict

Non-Deterministic Evolution

The evolution of Petri nets is not deterministic.
Any of the activated transactions might fire.

Some Definitions

Source transition: no inputs
Sink transition: no outputs
Self-loop: a pair $(p,t)$ s.t. $p$ is both an input and an output of $t$
Pure PN: no self-loops
Weighted PN: arcs with weight
Ordinary PN: all arc weights are 1's
Infinite capacity net: places can accommodate an unlimited number of tokens
Finite capacity net: each place p has a maximum capacity $K(p)$
strict transition rule: after firing, each output place can't have more than $K(p)$ tokens

Theorem: every pure finite-capacity net can be transformed into an equivalent infinite-capacity net

Weighted Edges

Associating weights to edges:

• Each edge fi has an associated weight W(fi) (defaults to 1)
• A transition $t$ is active if each place pi connected through an edge fi to t contains at least W(fi) tokens.

Finite Capacity Petri Net

Each place pi can hold maximally K(pi) tokens.

A transition t is only active if all output places pi of t cannot exceed K(pi) after firing t.

Pure finite capacity Petri Nets can be transformed into equivalent infinite capacity Petri Nets (without capacity restrictions).

Equivalence: Both nets have the same set of all possible firing sequences.

Removing Capacity Constraints

For each place p with $K(p)>1$, add a complementary place $p^{\prime }$ with initial marking $M_0(p^{\prime })=K(p)–M_0(p)$.

• For each outgoing edge $e=(p,t)$, add an edge $e^{\prime }$ from $t$ to $p^{\prime }$ with weight $W(e)$.
• For each incoming edge $e=(t,p)$, add an edge $e^{\prime }$ from $p^{\prime }$ to $t$ with weight $W(e)$.

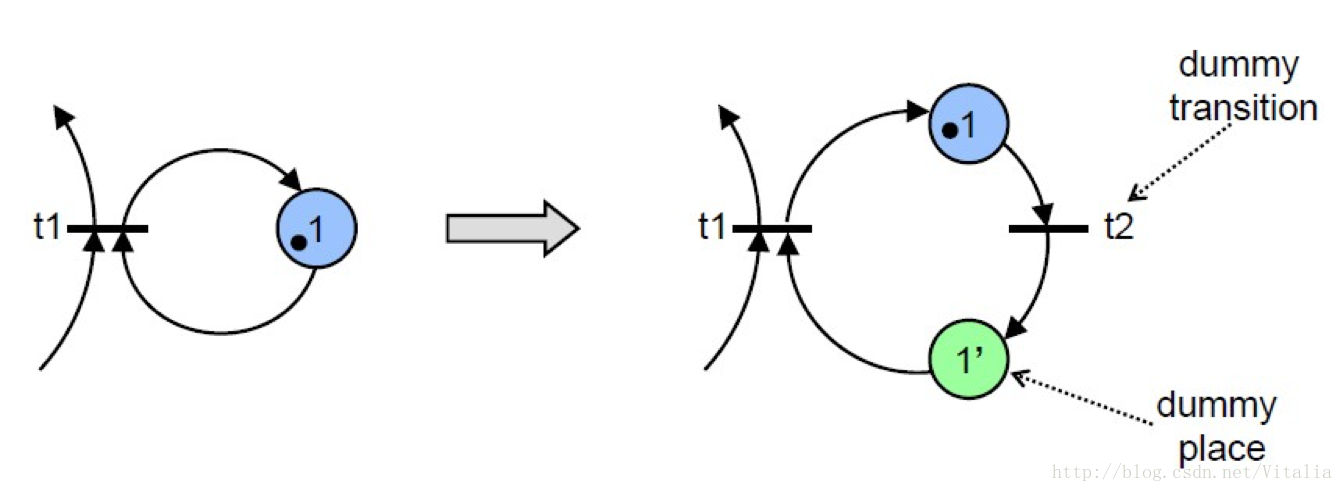
Resolving Self-Loops

The algorithm to remove capacity constraints works if the Petri net has no self loops (is pure).
No Problem! Rewrite the Petri net without self loops.

Behavioral properties

Properties that depend on the initial marking.

Reachability
$M_n$ is reachable from $M_0$ if exists a sequence of firings that transform $M_0$ into $M_n$
Reachability is decidable, but exponential.

Boundedness
A PN is bounded if the number of tokens in each place doesn't exceed a finite number k for any marking reachable from $M_0$
A PN is safe if it is 1-bounded.

Liveness
A PN is live if, no matter what marking has been reached, it is possible to fire any transition with an appropriate firing sequence
equivalent to deadlock-free

Reversibility
A PN is reversible if, for each marking M reachable from $M_0$, $M_0$ is reachable from $M$
Relaxed condition: a marking $M^{\prime }$ is a home state if, for each marking M reachable from M0, $M^{\prime }$ is reachable from $M$

Persistence
A PN is persistent if, for any two enabled transitions, the firing of one of them will not disable the other.
Then, once a transition is enabled, it remains enabled until it's fired.

Fairness
**Bounded-fairness: ** the number of times one transition can fire while the other is not firing is bounded
**Unconditional(global)-fairness: ** every transition appears infinitely often in a firing sequence

Coverability tree

Tree representation of all possible markings

• root = $M_0$
• nodes = markings reachable from $M_0$
• arcs = transition firings

If net is unbounded, then tree is kept finite by introducing the symbol $\omega$

Properties

• A PN is bounded iff $\omega$ doesn't appear in any node
• A PN is safe iff only 0's and 1's appear in nodes
• A transition is dead iff it doesn't appear in any arc
• If $M$ is reachable form $M_0$, then exists a node $M^{\prime }$ that covers $M$

Reduction Rules

Petri Net with Time

Time Petri nets are classical Petri Nets where to each transition t a time interval [a; b] is associated.

The times a and b are relative to the moment at which t was last enabled.

Assuming that t was enabled at time c, then t may fire only during the interval [c + a; c + b] and must fire at the time c + b at the latest, unless it is disabled before by the firing of another transition.

Firing a transition takes no time.

When a transition becomes enabled it may not fire at once (in general) but during a certain time interval and at the end of the interval there is a force to fire.

Let N be the set of natural numbers. A time Petri net is a six-tuple, $N=(P,T,F,Eft,Lft,{\mu }_0)$, where

• P = { p 1 , p 2 , … , p m } P = \{p_1, p_2, …, p_m\} P={p1​,p2​,…,pm​} is a finite set of places;
• T = { t 1 , t 2 , … , t n } T = \{t_1, t_2, …, t_n\} T={t1​,t2​,…,tn​} is a finite set of transitions $$(P\cap T=\varnothing )F\subset (P\times T)\cup (T\times P)$$ is the flow relation;
• $Eft,Lft:T\to N$ are functions for the earliest and latest firing times of transitions, satisfying that for any $t\in T$, $Eft(t)\le Lft(t)\le \infty$;
• ${\mu }_0\in P$ is the initial marking of the net.

A state of a time Petri net $N=(P,T,F,Eft,Lft,{\mu }_0)$, is a pair $s=(\mu ,c)$, where $\mu$ is a marking of N, and $c:enabled(\mu )\to T$ is called the clock function.

The initial state of N is $s_0=({\mu }_0,c_0)$ where $c_0(t)=0$ for any $t\in enabled({\mu }_0)$.

Untimed PNs represent sequences of firings, but these are logical sequences, not temporal ones.

Transitions in which the lower bound is 0 are called zero-time transitions, since they can occur at the same time in which they are enabled, without delay.

A Zeno behavior is one in which time does not advance.

One might argue that zero-time transitions in the real world cannot occur, so we should avoid them entirely.

However, even if they are not physically feasible, from the point of view of modeling they are often useful, for example to model cases in which the difference in time between two transitions is negligible with respect to the main dynamics of the system.

http://cpntools.org/_media/book/covgraph.pdf

Timed Automata

Peterson's Algorithm
Fischer's Protocol

Clock Constraints

Let X be a set of clock variables. Then set C(X) of clock constraints is given by the following grammar:$\phi \equiv x\le k|k\le x|x<k|k<x|\phi \wedge \phi$, where $x\in X$, $k\in N$.

Timed Automaton

Syntax

A timed automaton is a 4-tuple: $A=(L,X,l0,E)$.

• L is a finite set of locations
• X is a finite set of clocks
• $l_0\in L$ is an initial location
• $E\subseteq L\times C(X)\times 2X\times L$is a set of edges
  edge = (source location, clock constraint, set of clocks to be resetted, target location)

Semantics

Semantics is a state space.
***Reminder: *** guarded command language, extended finite state machines

States given by:

• location (local state of the automaton)
• clock valuation

Transitions:

• waiting – only clock valuation changes
• action – change of location

Clock valuation
A clock valuation is a function $\nu :X\to R^{+}$

• ν[Y := 0] is the valuation obtained from ν by resetting clocks from Y :
  $$\nu [Y:=0](x)=\{\begin{array}{rcl}0& & x\in Y\\ x& & otherwise\end{array}$$

• $\nu +d$ = flow of time ($d$ units):
  $$(\nu +d)(x)=\nu (x)+d$$

• $\nu \models c$ means that valuation $\nu$ satisfies the constraint $c$.

Evaluation of a clock constraint (ν |= g):
$\nu \models x<k$ iff $\nu (x)<k$
$\nu \models x\le k$ iff $\nu (x)\le k$
$\nu \models g1\wedge g2$ iff $\nu \models g_1$ and $\nu \models g_2$

Definition
The semantics of a timed automaton A is a transition system $S_A=(S,s_0,-\to )$:
$S=L\times (X\to R^{+})$
$s0=(l_0,{\nu }_0),{\nu }_0(x)=0$ for all $x\in X$
transition relation $\to \subseteq S\times S$ is defined as:

• (delay action) $(l,\nu )\to (l,\nu +\delta )$
• (discrete action) $(l,\nu )-\to (l\prime ,\nu \prime )$ iff there exists $(l,c,Y,l^{\prime })\in E$ such that $\nu |=c$, ${\nu }^{\prime }=\nu [Y:=0]$

the semantics is infinite state (even uncountable)
the semantics is even infinitely branching

Reachability Problem

Theorem：
The reachability problem is PSPACE-complete.
Notes
Note that even decidability of the problem is not straightforward — Remind that the semantics is infinite state
decidability proved by region construction
completeness proved by general reduction from linearly bounded Turing machine

https://www.fi.muni.cz/~xpelanek/IA158/slides/timed-automata.pdf