一、引例

1、vector 扩容概述

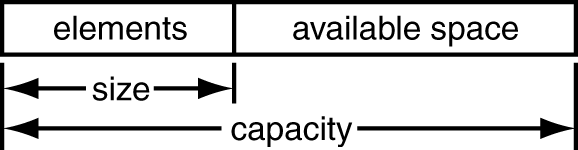
• 我们知道，STL 的 vector 底层实现是动态数组，大致原理就是：vector 为空的时候没有预分配空间，每次添加一个元素时，会判断当前是否还有剩余可用空间，如果没有则进行试探性扩容，并且把内存拷贝到新申请的内存空间上，并且释放原先的内存；

2、扩容时机

• size 大于 capacity；

3、扩容尝试

• size 代表了已经使用的空间；
• capacity 代表上次使用申请的预分配空间数；
• 这边做了一个表，列举了 VS2013 环境下 vector 在一个一个插入元素 （push_back）的过程中，size 和 capacity 的对应关系；

• 可能仔细观察也能观察出来，扩容的策略是 0.5倍倍增 capacity，然后做一个简单修正，具体的实现逻辑听我慢慢道来；

二、扩容逻辑解析

1、扩容逻辑实现

• 扩容成多大是由 _Grow_to 函数实现的：

    // grow by 50% or at least to _Count
	size_type _Grow_to(size_type _Count) const
	{
		size_type _Capacity = capacity();

		_Capacity = max_size() - _Capacity / 2 < _Capacity 
		? 0 : _Capacity + _Capacity / 2;	// try to grow by 50%
		
		if (_Capacity < _Count)
			_Capacity = _Count;
		
		return (_Capacity);
	}

• max_size() 是一个很大的数，基本可以不考虑，如果能够达到，内存基本也不够用，所以这个逻辑理解的时候可以精简一下；

2、精简后的扩容逻辑

• 精简后就成了下面的代码：

    _Capacity = _Capacity + _Capacity / 2;         // 增加一半容量(/2是下取整的)
    if (_Capacity < _Count) _Capacity = _Count;    // 至少到 _Count，这里的 _Count 在 push_back 的情况下为 size + 1

• 核心逻辑1：按照 _Capacity/2 的下整，累加 _Capacity 的值；
• 核心逻辑2：取 max(_Capacity, _Count) 作为新的 _Capacity；
• 核心逻辑3：push_back的情况下，_Count = size + 1；

3、验证扩容逻辑

4、优化

• capacity 每改变一次，就会进行一次空间重分配；
• 观察发现，这个策略下，vector 元素一个一个 push_back 的时候，从 size = 1 到 5，每次都进行了空间重分配；
• 因为每次空间重分配，势必导致数据迁移，涉及到数据的申请和释放，会影响程序运行效率，所以一般可以利用 reserve 接口预分配一些空间；

三、论文解读补充

• 关于倍增法的时间复杂度问题，找到了一篇论文，大致翻译整理成文，希望读者能够看懂；
• 论文地址：https://www.drdobbs.com/c-made-easier-how-vectors-grow/184401375

1、Size 和 Capacity

• 1）vector 本身不仅仅是一块连续的内存，它有两个表示大小的值，一个叫Size，一个叫 Capacity；
• 2）Size代表已经用了的元素的大小，Capacity表示总共元素的大小；

]

• 3）当调用 push_back 的时候，如果剩余空间还有，则不需要重新分配新的空间；否则，需要对 vector 进行内存重分配；

2、内存重分配

• 内存重分配的步骤为：
• 1）根据新指定的 Capacity 分配对应的内存空间；
• 2）将数据从旧的内存拷贝到新申请的内存；
• 3）析构旧内存的数据；
• 4）释放旧内存的空间；

3、内存重分配策略

• 1）方案1：如果每次 push_back 的时候，都需要增长 Capacity 的值，也就是每次 Capacity 加 1，那么当有k个元素的时候，重新分配内存需要的时间是 O(k)，添加完 n 个元素的总时间复杂度就是 O(1+2+…+n) = O(n^2)，这样效率太低了；
• 2）方案2：如果每次 push_back 的时候，当没有剩余可用空间时，给 Capacity 增加一个常数因子 C（C > 1），这样势必会比第一种方法更加有效的减少了内存重分配的次数，但是均摊复杂度还是 O(n^2) 的，只不过常数小了；
• 3）方案3：如果每次 push_back 的时候，当没有剩余可用空间时，给 Capacity 进行一次倍增，这个内存重分配的复杂度是多少呢？

4、倍增法时间复杂度分析

• 某一次内存重分配完了以后， Capacity 达到了 n，那么表示这里有 n/2 个位置的元素是空的，剩下 n/2 的一半元素被拷贝了1次，剩下的一半的一半的元素拷贝了2次，etc；
• 那么所有元素被拷贝的次数就是：

    n/4 * 1 + n/8 * 2 + n/16 * 4 + ... = n

• 所以倍增法的总体时间复杂度是 O(n) 的；