1️⃣前言:追忆我的刷题经历
学习算法最好的方法就是刷题了,上大学的时候刷过一些,最近开始转战 LeetCode。
🔥让天下没有难学的算法🔥
C语言免费动漫教程,和我一起打卡! 🌞《光天化日学C语言》🌞
入门级C语言真题汇总 🧡《C语言入门100例》🧡
几张动图学会一种数据结构 🌳《画解数据结构》🌳
组团学习,抱团生长 🌌《算法入门指引》🌌
竞赛选手金典图文教程 💜《夜深人静写算法》💜
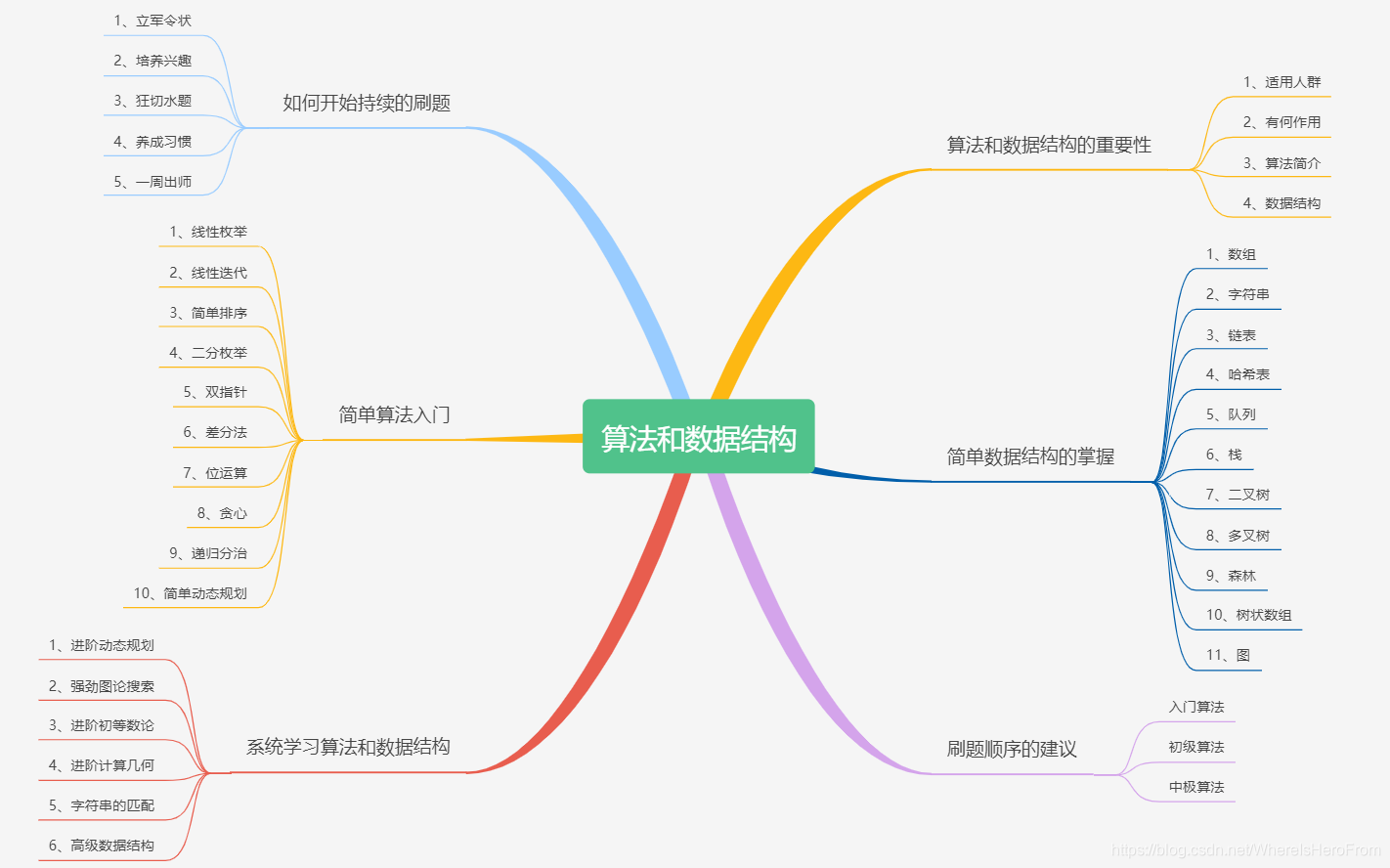
2️⃣算法和数据结构的重要性
👪1、适用人群
- 这篇文章会从 「算法和数据结构」 零基础开始讲,所以,如果你是算法大神,可以尽情在评论区嘲讽我哈哈,目的当然是帮助想要涉足算法领域,或者正在找工作的朋友,以及将要找工作的大学生,更加有效快速的掌握算法思维,能够在职场面试和笔试中一展身手。
- 这篇文章中,我会着重讲解一些常见的 「算法和数据结构」 的设计思想,并且配上动图。主要针对面试中常见的问题和新手朋友们比较难理解的点进行解析。当然,后面也会给出面向算法竞赛的提纲,如果有兴趣深入学习的欢迎在评论区留言,一起成长交流。
- 零基础学算法的最好方法,莫过于刷题了。任何事情都是需要坚持的,刷题也一样,没有刷够足够的题,就很难做出系统性的总结。所以上大学的时候,我花了三年的时间来刷题, 工作以后还是会抽点时间出来刷题。
千万不要用工作忙来找借口,时间挤一挤总是有的。
- 我现在上班地铁上一个小时,下班地铁又是一个小时。比如这篇文章的起草,就是在 地铁 上完成的。如何利用这两个小时的时间,做一些有建设性的事情,才是最重要的。刷抖音一个小时过得很快,刷题也是同样的道理。
- 当然,每天不需要花太多时间在这个上面,把这个事情做成一个规划,按照长期去推进。反正也没有 KPI 压力,就当成是工作之余的一种消遣,还能够提升思维能力。何乐而不为!
所以,无论你是 小学生,中学生,高中OIer,大学ACMer,职场人士,只要想开始,一切都不会太晚!
🎾2、有何作用
- 我们平常使用的 智能手机、搜索引擎、网站、操作系统、游戏、软件、人工智能,都大量地应用了 「算法与数据结构」 的知识,以及平时你用到的各种库的底层实现,也是通过各种算法和数据结构组合出来的,所以可以说,有程序的地方,就有
江湖算法,有算法就一定会有对应的数据结构。 - 如果你只是想学会写代码,或许 「算法与数据结构」 并不是那么重要,但是想要往更深一步发展,「算法与数据结构」 是必不可少的。
现在一些主流的大厂,在面试快结束的时候都会 奉上一道算法题,如果你敲不出来,可能你的 offer 年包就打了 七折,或者直接与 offer 失之交臂,都是有可能的(因为我自己也是万恶的面试官,看到候选人的算法题写不出来我也是操碎了心,但是我一般会给足容错,比如给三个算法题,挑一个写,任意写出一个都行)。
- 当然,它不能完全代表你的编码能力,因为有些算法确实是很巧妙,加上紧张的面试氛围,想不出来其实也是正常的,但是你能确保面试官是这么想的吗?我们要做的是十足的准备,既然决定出来,offer 当然是越高越好,毕竟大家都要养家糊口,房价又这么贵,如果能够在算法这一块取得先机,也不失为一个捷径。
所以,你问我算法和数据结构有什么用?我可以很明确的说,和你的年薪息息相关。
- 当然,面试中 「算法与数据结构」 知识的考察只是面试内容的一部分。其它还有很多面试要考察的内容,当然不是本文主要核心内容,这里就不做展开了。
📜3、算法简介
- 算法是什么东西?
- 它是一种方法,一种解决问题的方案。
- 举个例子,你现在要去上班,可以选择 走路、跑步、坐公交、坐地铁、自己开车 等等,这些都是解决方案。但是它们都会有一些衡量指标,让你有一个权衡,最后选择你认为最优的策略去做。
- 而衡量的指标诸如:时间消耗、金钱消耗、是否需要转车、是否可达 等等。
时间消耗就对应了:时间复杂度
金钱消耗就对应了:空间复杂度
是否可达就对应了:算法可行性
- 当然,是否需要转车,从某种程度上都会影响 时间复杂度 或者 空间复杂度。
🌲4、数据结构
- 对于实现某个算法,我们往往会用到一些数据结构。
- 因为我们通常不能一下子把数据处理完,更多的时候需要先把它们放在一个容器或者说缓存里面,等到一定的时刻再把它们拿出来。
- 这其实是一种 「空间换时间」 思想的体现, 恰当使用数据结构可以帮助我们高效地处理数据。
- 常用的一些数据结构如下:
| 数据结构 | 应用场景 |
|---|---|
| 数组 | 线性存储、元素为任意相同类型、随机访问 |
| 字符串 | 线性存储、元素为字符、结尾字符、随机访问 |
| 链表 | 链式存储、快速删除 |
| 栈 | 先进后出 |
| 队列 | 先进先出 |
| 哈希表 | 随机存储、快速增删改查 |
| 二叉树 | 对数时间增删改查,二叉查找树、线段树 |
| 多叉树 | B/B+树 硬盘树、字典树 字符串前缀匹配 |
| 森林 | 并查集 快速合并数据 |
| 树状数组 | 单点更新,成段求和 |
- 为什么需要引入这么多数据结构呢?
答案是:任何一种数据结构是不是 完美的。所以我们需要根据对应的场景,来采用对应的数据结构,具体用哪种数据结构,需要通过刷题不断刷新经验,才能总结出来。
3️⃣如何开始持续的刷题
- 有朋友告诉我,题目太难了,根本不会做,每次都是看别人的解题报告。
📑1、立军令状
- 所谓 「军令状」,其实就是给自己定一个目标,给自己树立一个目标是非常重要的,有 「目标才会有方向,有目标才会有动力,有目标才会有人生的意义」 。而军令状是贬义的,如果不达成就会有各种惩罚,所以其实你是心不甘情不愿的,于是这件事情其实是无法持久下去的。
事实证明,立军令状是不可取的。
- 啊这……所以我们还是要采用一些能够持久下去的方法。
👩❤️👩2、培养兴趣
- 为了让这件事情能够持久下去,一定要培养出兴趣,适时的给自己一些正反馈。正反馈的作用就是每过一个周期,如果效果好,就要有奖励,这个奖励机制可以自己设定,但是 「不能作弊」 ,一旦作弊就像单机游戏修改数值,流失是迟早的事。
- 举个例子,我们可以给每天制定一些 「不一样的目标和奖励」 ,比如下图所示:
| 刷题的第?天 | 目标题数 | 是否完成 | 完成奖励 |
|---|---|---|---|
| 1 | 1 | ? | 攻击力 + 10 |
| 2 | 1 | ? | 防御力 + 10 |
| 3 | 2 | ? | 出去吃顿好的 |
| 4 | 2 | ? | 攻击力 + 29 |
| 5 | 3 | ? | 防御力 + 60 |
| 6 | 1 | ? | 攻击力 + 20 |
| 7 | 4 | ? | 出去吃顿好的 |
| 8 | 1 | ? | 防御力 + 50 |
- 当然,这个完成奖励你可以自己定,总而言之,要是对你有诱惑的奖励才是有意义的。
🚿3、狂切水题
- 刚开始刷的 300 题一定都是 「水题」 ,刷 「水题」 的目的是让你养成一个每天刷题的习惯。久而久之,不刷题的日子会变得无比煎熬。当然,刷着刷着,你会发现,水题会越来越多,因为刷题的过程中,你已经无形中不断成长起来了。
- 至少这个方法我用过,非常灵验!推荐刷题从水题开始。
如果不知道哪里有水题,推荐:
C语言入门水题:《C语言入门100例》
C语言算法水题:《LeetCode算法全集》
💪🏻4、养成习惯
- 相信如果切了 300 个 「水题」 以后,刷题自然而然就成了习惯,想放弃都难。这个专业上讲,其实叫 沉没成本。有兴趣的可以自行百度,这里就不再累述了。
🈵5、一周出师
- 基本上如果能够按照这样的计划去执行,一周以后,一定会有收获,没有收获的话,可以来找我。
4️⃣简单数据结构的掌握
🚂1、数组
内存结构:内存空间连续
实现难度:简单
下标访问:支持
分类:静态数组、动态数组
插入时间复杂度: O ( n ) O(n) O(n)
查找时间复杂度: O ( n ) O(n) O(n)
删除时间复杂度: O ( n ) O(n) O(n)
🎫2、字符串
内存结构:内存空间连续,类似字符数组
实现难度:简单,一般系统会提供一些方便的字符串操作函数
下标访问:支持
插入时间复杂度: O ( n ) O(n) O(n)
查找时间复杂度: O ( n ) O(n) O(n)
删除时间复杂度: O ( n ) O(n) O(n)
🎇3、链表
内存结构:内存空间连续不连续,看具体实现
实现难度:一般
下标访问:不支持
分类:单向链表、双向链表、循环链表、DancingLinks
插入时间复杂度: O ( 1 ) O(1) O(1)
查找时间复杂度: O ( n ) O(n) O(n)
删除时间复杂度: O ( 1 ) O(1) O(1)
🌝4、哈希表
内存结构:哈希表本身连续,但是衍生出来的结点逻辑上不连续
实现难度:一般
下标访问:不支持
分类:正数哈希、字符串哈希、滚动哈希
插入时间复杂度: O ( 1 ) O(1) O(1)
查找时间复杂度: O ( 1 ) O(1) O(1)
删除时间复杂度: O ( 1 ) O(1) O(1)
- 哈希表相关的内容,可以参考我的这篇文章:
- 夜深人静写算法(九)- 哈希表
👨👩👧5、队列
内存结构:看用数组实现,还是链表实现
实现难度:一般
下标访问:不支持
分类:FIFO、单调队列、双端队列
插入时间复杂度: O ( 1 ) O(1) O(1)
查找时间复杂度:理论上不支持
删除时间复杂度: O ( 1 ) O(1) O(1)
- 队列相关的内容,可以参考我的这篇文章:
- 夜深人静写算法(十)- 单向广搜
👩👩👦👦6、栈
内存结构:看用数组实现,还是链表实现
实现难度:一般
下标访问:不支持
分类:FILO、单调栈
插入时间复杂度: O ( 1 ) O(1) O(1)
查找时间复杂度:理论上不支持
删除时间复杂度: O ( 1 ) O(1) O(1)
- 栈相关的内容,可以参考我的这篇文章:
- 夜深人静写算法(十一)- 单调栈
🌵7、二叉树
优先队列 是 堆实现的,所以也属于 二叉树 范畴。它和队列不同,不属于线性表。
内存结构:内存结构一般不连续,但是有时候实现的时候,为了方便,一般是物理连续,逻辑不连续
实现难度:较难
下标访问:不支持
分类:二叉树 和 多叉树
插入时间复杂度:看情况而定
查找时间复杂度:理论上 O ( l o g 2 n ) O(log_2n) O(log2n)
删除时间复杂度:看情况而定
🌳8、多叉树
内存结构:内存结构一般不连续,但是有时候实现的时候,为了方便,一般是物理连续,逻辑不连续
实现难度:较难
下标访问:不支持
分类:二叉树 和 多叉树
插入时间复杂度:看情况而定
查找时间复杂度:理论上 O ( l o g 2 n ) O(log_2n) O(log2n)
删除时间复杂度:看情况而定
- 一种经典的多叉树是字典树,可以参考我的这篇文章:
- 夜深人静写算法(七)- 字典树
🌲9、森林
- 比较经典的森林是:并查集,可以参考我的这篇文章:
- 夜深人静写算法(五)- 并查集
🍀10、树状数组
- 树状数组是用来做 单点更新,成端求和 的问题的,有关于它的内容,可以参考:
- 夜深人静写算法(十三)- 树状数组
🌍11、图
内存结构:不一定
实现难度:难
下标访问:不支持
分类:有向图、无向图
插入时间复杂度:根据算法而定
查找时间复杂度:根据算法而定
删除时间复杂度:根据算法而定
1、图的概念
- 在讲解最短路问题之前,首先需要介绍一下计算机中图(图论)的概念,如下:
- 图 G G G 是一个有序二元组 ( V , E ) (V,E) (V,E),其中 V V V 称为顶点集合, E E E 称为边集合, E E E 与 V V V 不相交。顶点集合的元素被称为顶点,边集合的元素被称为边。
- 对于无权图,边由二元组 ( u , v ) (u,v) (u,v) 表示,其中 u , v ∈ V u, v \in V u,v∈V。对于带权图,边由三元组 ( u , v , w ) (u,v, w) (u,v,w) 表示,其中 u , v ∈ V u, v \in V u,v∈V, w w w 为权值,可以是任意类型。
- 图分为有向图和无向图,对于有向图, ( u , v ) (u, v) (u,v) 表示的是 从顶点 u u u 到 顶点 v v v 的边,即 u → v u \to v u→v;对于无向图, ( u , v ) (u, v) (u,v) 可以理解成两条边,一条是 从顶点 u u u 到 顶点 v v v 的边,即 u → v u \to v u→v,另一条是从顶点 v v v 到 顶点 u u u 的边,即 v → u v \to u v→u;
2、图的存储
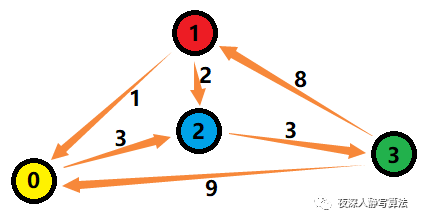
- 对于图的存储,程序实现上也有多种方案,根据不同情况采用不同的方案。接下来以图二-3-1所表示的图为例,讲解四种存储图的方案。
1)邻接矩阵
- 邻接矩阵是直接利用一个二维数组对边的关系进行存储,矩阵的第 i i i 行第 j j j 列的值 表示 i → j i \to j i→j 这条边的权值;特殊的,如果不存在这条边,用一个特殊标记 ∞ \infty ∞ 来表示;如果 i = j i = j i=j,则权值为 0 0 0。
- 它的优点是:实现非常简单,而且很容易理解;缺点也很明显,如果这个图是一个非常稀疏的图,图中边很少,但是点很多,就会造成非常大的内存浪费,点数过大的时候根本就无法存储。
- [ 0 ∞ 3 ∞ 1 0 2 ∞ ∞ ∞ 0 3 9 8 ∞ 0 ] \left[ \begin{matrix} 0 & \infty & 3 & \infty \\ 1 & 0 & 2 & \infty \\ \infty & \infty & 0 & 3 \\ 9 & 8 & \infty & 0 \end{matrix} \right] ⎣⎢⎢⎡01∞9∞0∞8320∞∞∞30⎦⎥⎥⎤
2)邻接表
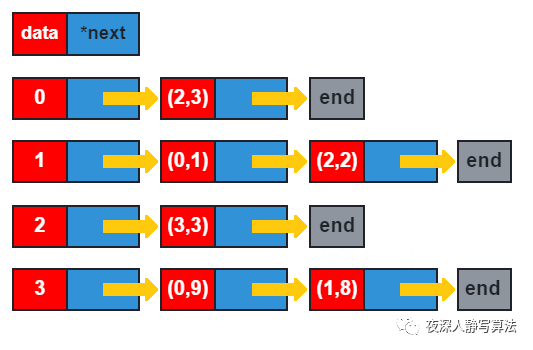
- 邻接表是图中常用的存储结构之一,采用链表来存储,每个顶点都有一个链表,链表的数据表示和当前顶点直接相邻的顶点的数据 ( v , w ) (v, w) (v,w),即 顶点 和 边权。
- 它的优点是:对于稀疏图不会有数据浪费;缺点就是实现相对邻接矩阵来说较麻烦,需要自己实现链表,动态分配内存。
- 如图所示,
d
a
t
a
data
data 即
(
v
,
w
)
(v, w)
(v,w) 二元组,代表和对应顶点
u
u
u 直接相连的顶点数据,
w
w
w 代表
u
→
v
u \to v
u→v 的边权,
n
e
x
t
next
next 是一个指针,指向下一个
(
v
,
w
)
(v, w)
(v,w) 二元组。
- 在 C++ 中,还可以使用 vector 这个容器来代替链表的功能;
vector<Edge> edges[maxn];
3)前向星
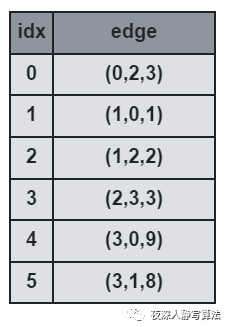
- 前向星是以存储边的方式来存储图,先将边读入并存储在连续的数组中,然后按照边的起点进行排序,这样数组中起点相等的边就能够在数组中进行连续访问了。
- 它的优点是实现简单,容易理解;缺点是需要在所有边都读入完毕的情况下对所有边进行一次排序,带来了时间开销,实用性也较差,只适合离线算法。
- 如图所示,表示的是三元组
(
u
,
v
,
w
)
(u, v, w)
(u,v,w) 的数组,
i
d
x
idx
idx 代表数组下标。
- 那么用哪种数据结构才能满足所有图的需求呢?
- 接下来介绍一种新的数据结构 —— 链式前向星。
4)链式前向星
- 链式前向星和邻接表类似,也是链式结构和数组结构的结合,每个结点 i i i 都有一个链表,链表的所有数据是从 i i i 出发的所有边的集合(对比邻接表存的是顶点集合),边的表示为一个四元组 ( u , v , w , n e x t ) (u, v, w, next) (u,v,w,next),其中 ( u , v ) (u, v) (u,v) 代表该条边的有向顶点对 u → v u \to v u→v, w w w 代表边上的权值, n e x t next next 指向下一条边。
- 具体的,我们需要一个边的结构体数组
edge[maxm],maxm表示边的总数,所有边都存储在这个结构体数组中,并且用head[i]来指向 i i i 结点的第一条边。 - 边的结构体声明如下:
struct Edge {
int u, v, w, next;
Edge() {}
Edge(int _u, int _v, int _w, int _next) :
u(_u), v(_v), w(_w), next(_next)
{
}
}edge[maxm];
- 初始化所有的
head[i] = -1,当前边总数edgeCount = 0; - 每读入一条
u
→
v
u \to v
u→v 的边,调用
addEdge(u, v, w),具体函数的实现如下:
void addEdge(int u, int v, int w) {
edge[edgeCount] = Edge(u, v, w, head[u]);
head[u] = edgeCount++;
}
- 这个函数的含义是每加入一条边 ( u , v , w ) (u, v, w) (u,v,w),就在原有的链表结构的首部插入这条边,使得每次插入的时间复杂度为 O ( 1 ) O(1) O(1),所以链表的边的顺序和读入顺序正好是逆序的。这种结构在无论是稠密的还是稀疏的图上都有非常好的表现,空间上没有浪费,时间上也是最小开销。
- 调用的时候只要通过
head[i]就能访问到由 i i i 出发的第一条边的编号,通过编号到edge数组进行索引可以得到边的具体信息,然后根据这条边的next域可以得到第二条边的编号,以此类推,直到next域为 -1 为止。
for (int e = head[u]; ~e; e = edges[e].next) {
int v = edges[e].v;
ValueType w = edges[e].w;
...
}
- 文中的
~e等价于e != -1,是对e进行二进制取反的操作(-1 的的补码二进制全是 1,取反后变成全 0,这样就使得条件不满足跳出循环)。
5️⃣简单算法的入门
- 入门十大算法是 线性枚举、线性迭代、简单排序、二分枚举、双指针、差分法、位运算、贪心、分治递归、简单动态规划。
- 对于这十大算法,我会逐步更新道这个专栏里面:《LeetCode算法全集》。
- 浓缩版可参考如下文章:《十大入门算法》
🚊10、简单动态规划
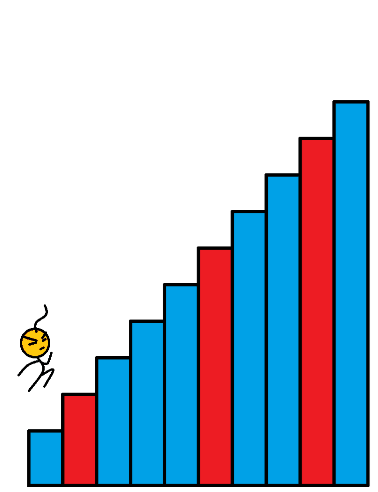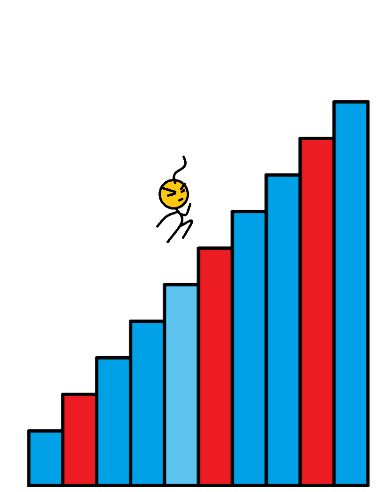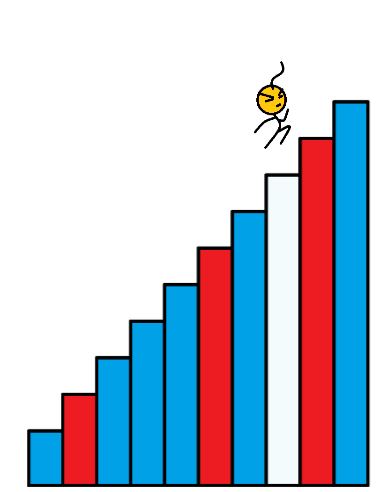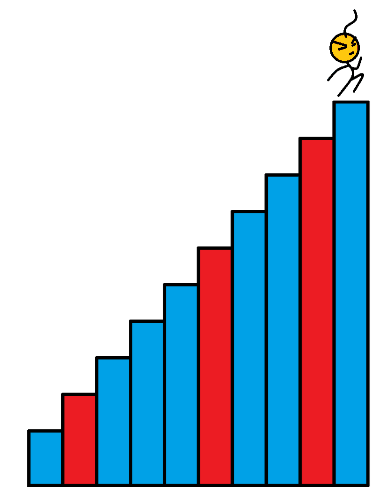
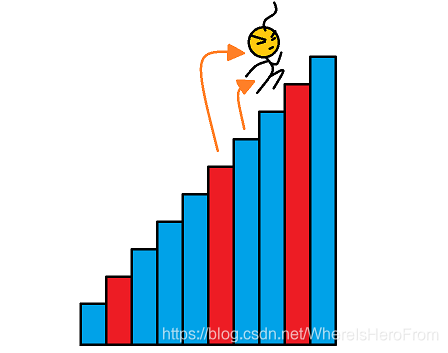
数组的每个下标作为一个阶梯,第 i i i 个阶梯对应着一个非负数的体力花费值 c o s t [ i ] cost[i] cost[i](下标从 0 开始)。每当爬上一个阶梯,都要花费对应的体力值,一旦支付了相应的体力值,就可以选择 向上爬一个阶梯 或者 爬两个阶梯。求找出达到楼层顶部的最低花费。在开始时,可以选择从下标为 0 或 1 的元素作为初始阶梯。
样例输入: c o s t = [ 1 , 99 , 1 , 1 , 1 , 99 , 1 , 1 , 99 , 1 ] cost = [1, 99, 1, 1, 1, 99, 1, 1, 99, 1] cost=[1,99,1,1,1,99,1,1,99,1]
样例输出: 6 6 6
如图所以,蓝色的代表消耗为 1 的楼梯,红色的代表消耗 99 的楼梯。
a、思路分析
- 令走到第 i i i 层的最小消耗为 f [ i ] f[i] f[i]
- 假设当前的位置在 i i i 层楼梯,那么只可能从 i − 1 i-1 i−1 层过来,或者 i − 2 i-2 i−2 层过来;
- 如果从 i − 1 i-1 i−1 层过来,则需要消耗体力值: f [ i − 1 ] + c o s t [ i − 1 ] f[i-1] + cost[i-1] f[i−1]+cost[i−1];
- 如果从 i − 2 i-2 i−2 层过来,则需要消耗体力值: f [ i − 2 ] + c o s t [ i − 2 ] f[i-2] + cost[i-2] f[i−2]+cost[i−2];
- 起点可以在第 0 或者 第 1 层,于是有状态转移方程:
-
f
[
i
]
=
{
0
i
=
0
,
1
min
(
f
[
i
−
1
]
+
c
o
s
t
[
i
−
1
]
,
f
[
i
−
2
]
+
c
o
s
t
[
i
−
2
]
)
i
>
1
f[i] = \begin{cases} 0 & i=0,1\\ \min ( f[i-1] + cost[i-1], f[i-2] + cost[i-2] ) & i > 1\end{cases}
f[i]={0min(f[i−1]+cost[i−1],f[i−2]+cost[i−2])i=0,1i>1
b. 时间复杂度
- 状态数: O ( n ) O(n) O(n)
- 状态转移: O ( 1 ) O(1) O(1)
- 时间复杂度: O ( n ) O(n) O(n)
c. 代码详解
class Solution {
int f[1100]; // (1)
public:
int minCostClimbingStairs(vector<int>& cost) {
f[0] = 0, f[1] = 0; // (2)
for(int i = 2; i <= cost.size(); ++i) {
f[i] = min(f[i-1] + cost[i-1], f[i-2] + cost[i-2]); // (3)
}
return f[cost.size()];
}
};
-
(
1
)
(1)
(1) 用
f[i]代表到达第 i i i 层的消耗的最小体力值。 - ( 2 ) (2) (2) 初始化;
- ( 3 ) (3) (3) 状态转移;
有没有发现,这个问题和斐波那契数列很像,只不过斐波那契数列是求和,这里是求最小值。
6️⃣刷题顺序的建议
然后介绍一下刷题顺序的问题,我们刷题的时候千万不要想着一步到位,一开始,没有刷满三百题,姿态放低,都把自己当成小白来处理。
这里以刷 LeetCode 为例,我目前只刷了不到 50 题,所以我是小白。
当我是小白时,我只刷入门题,也就是下面这几个专题。先把上面所有的题目刷完,在考虑下一步要做什么。
👨👦1、入门算法
| 种类 | 链接 |
|---|---|
| 算法 | 算法入门 |
| 数据结构 | 数据结构入门 |
| 数组字符串专题 | 数组和字符串 |
| 动态规划专题 | 动态规划入门、DP路径问题 |
当入门的题刷完了,并且都能讲述出来自己刷题的过程以后,我们再来看初级的一些算法和简单的数据结构,简单的数据结构就是线性表了,包含:数组、字符串、链表、栈、队列 等等,即下面这些专题。
👩👧👦2、初级算法
| 种类 | 链接 |
|---|---|
| 算法 | 初级算法 |
| 栈和队列专题 | 队列 & 栈 |
上面的题刷完以后,其实已经算是基本入门了,然后就可以开始系统性的学习了。
当然,基本如果真的到了这一步,说明你的确已经爱上了刷题了,那么我们可以尝试挑战一下 LeetCode 上的一些热门题,毕竟热门题才是现在面试的主流,能够有更好的结果,这样刷题的时候也会有更加强劲的动力不是吗!
👩👩👧👦3、中级算法
| 种类 | 链接 |
|---|---|
| 算法 | 中极算法 |
| 二叉树专题 | 二叉树 |
| 热门题 | 热门题 TOP 100 |
7️⃣系统学习算法和数据结构
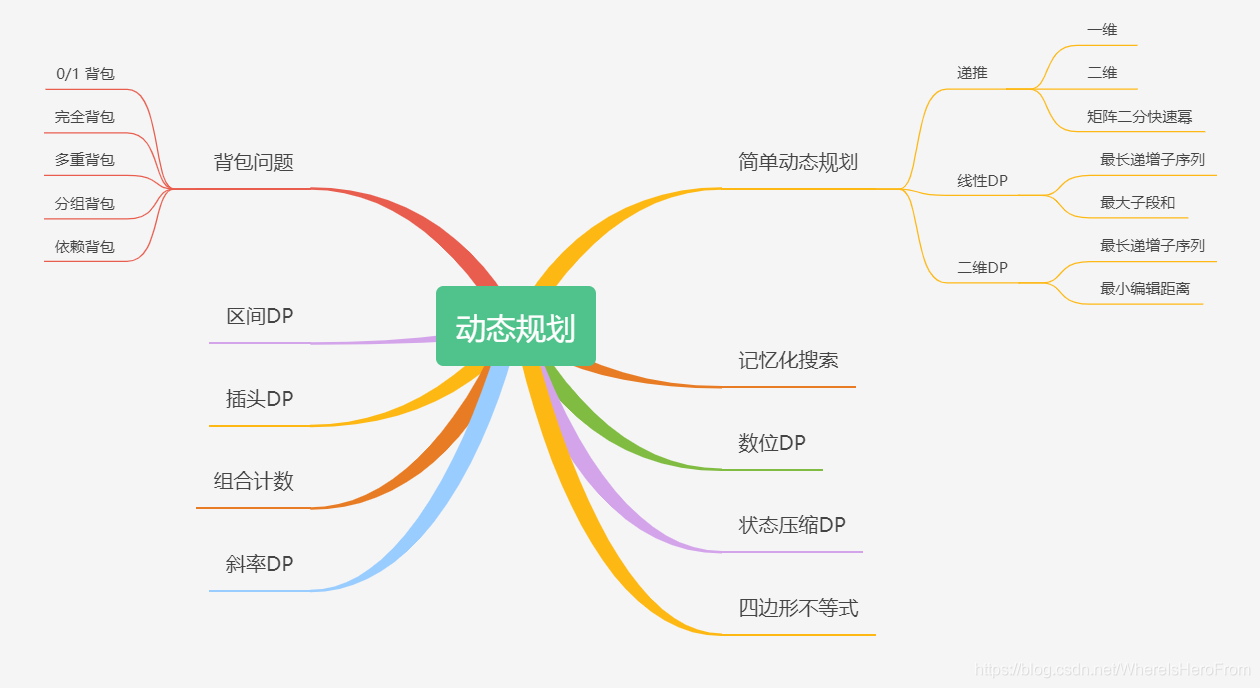
🚍1、进阶动态规划
| 文章链接 | 难度等级 | 推荐阅读 |
|---|---|---|
| 夜深人静写算法(二)- 动态规划入门 | ★☆☆☆☆ | ★★★★★ |
| 夜深人静写算法(二十六)- 记忆化搜索 | ★☆☆☆☆ | ★★★★★ |
| 夜深人静写算法(十九)- 背包总览 | ★☆☆☆☆ | ★★★★★ |
| 夜深人静写算法(二十)- 最长单调子序列 | ★☆☆☆☆ | ★★★★★ |
| 夜深人静写算法(二十一)- 最长公共子序列 | ★☆☆☆☆ | ★★★★★ |
| 夜深人静写算法(二十二)- 最小编辑距离 | ★★☆☆☆ | ★★★★☆ |
| 夜深人静写算法(十四)- 0/1 背包 | ★☆☆☆☆ | ★★★★☆ |
| 夜深人静写算法(十五)- 完全背包 | ★★☆☆☆ | ★★★★☆ |
| 夜深人静写算法(十六)- 多重背包 | ★★☆☆☆ | ★★★★☆ |
| 夜深人静写算法(二十七)- 区间DP | ★★★☆☆ | ★★★★☆ |
| 夜深人静写算法(二十九)- 数位DP | ★★★☆☆ | ★★★★★ |
| 夜深人静写算法(十七)- 分组背包 | ★★★☆☆ | ★★★☆☆ |
| 夜深人静写算法(十八)- 依赖背包 | ★★★★☆ | ★★☆☆☆ |
| 夜深人静写算法(六)- RMQ | ★★★☆☆ | ★★☆☆☆ |
| 树形DP | 待更新 | … |
| 组合博弈 | 待更新 | … |
| 组合计数DP | 待更新 | … |
| 四边形不等式 | 待更新 | … |
| 状态压缩DP/TSP | 待更新 | … |
| 斜率优化的动态规划 | 待更新 | … |
| 插头DP | 待更新 | … |
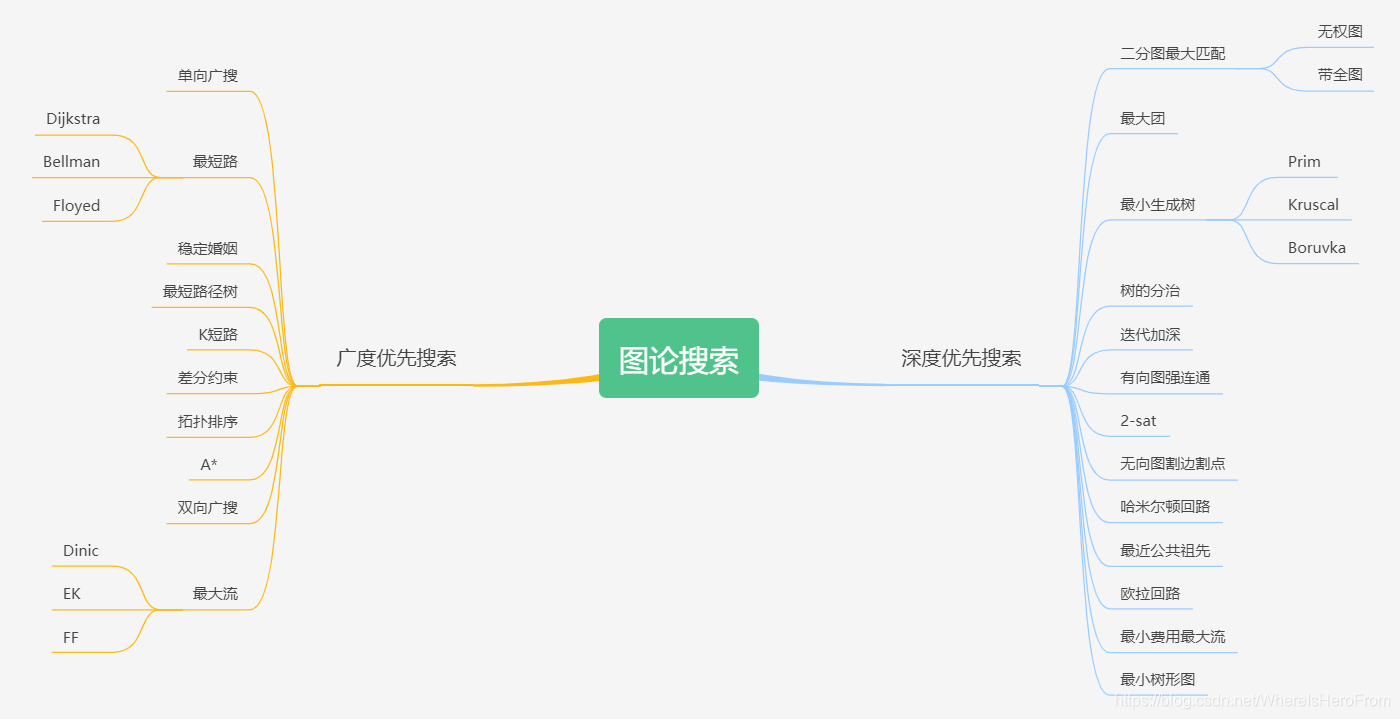
🪐2、强劲图论搜索
1、深度优先搜索
| 文章链接 | 难度等级 | 推荐阅读 |
|---|---|---|
| 夜深人静写算法(一)- 搜索入门 | ★☆☆☆☆ | ★★★☆☆ |
| 夜深人静写算法(八)- 二分图最大匹配 | ★★☆☆☆ | ★★☆☆☆ |
| 最大团 | 待更新 | … |
| 最小生成树 | 待更新 | … |
| 树的分治 | 待更新 | … |
| 迭代加深 IDA* | 待更新 | … |
| 有向图强连通分量和2-sat | 待更新 | … |
| 无向图割边割点 | 待更新 | … |
| 带权图的二分图匹配 | 待更新 | … |
| 哈密尔顿回路 | 待更新 | … |
| 最近公共祖先 | 待更新 | … |
| 欧拉回路圈套圈 | 待更新 | … |
| 最小费用最大流 | 待更新 | … |
| 最小树形图 | 待更新 | … |
2、广度优先搜索
| 文章链接 | 难度等级 | 推荐阅读 |
|---|---|---|
| 夜深人静写算法(十)- 单向广搜 | ★★☆☆☆ | ★★★★☆ |
| 夜深人静写算法(二十三)- 最短路 | ★★★☆☆ | ★★★★☆ |
| 夜深人静写算法(二十五)- 稳定婚姻 | ★★☆☆☆ | ★★☆☆☆ |
| 夜深人静写算法(二十四)- 最短路径树 | ★★★☆☆ | ★☆☆☆☆ |
| K 短路 | 待更新 | … |
| 差分约束 | 待更新 | … |
| 拓扑排序 | 待更新 | … |
| A* | 待更新 | … |
| 双向广搜 | 待更新 | … |
| 最大流 最小割 | 待更新 | … |
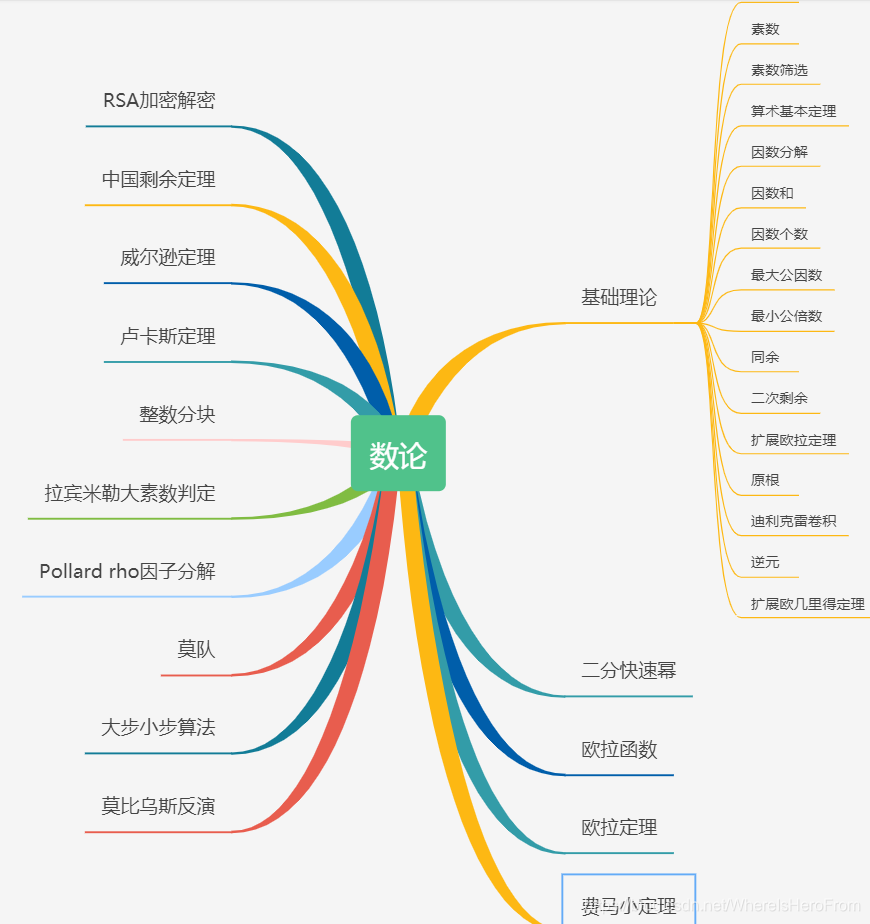
0️⃣3、进阶初等数论
| 文章链接 | 难度等级 | 推荐阅读 |
|---|---|---|
| 夜深人静写算法(三)- 初等数论入门 | ★★☆☆☆ | ★★★★☆ |
| 夜深人静写算法(三十)- 二分快速幂 | ★☆☆☆☆ | ★★★★★ |
| 夜深人静写算法(三十一)- 欧拉函数 | ★★★☆☆ | ★★★★★ |
| 夜深人静写算法(三十二)- 费马小定理 | ★★☆☆☆ | ★★★☆☆ |
| 夜深人静写算法(三十三)- 扩展欧拉定理 | ★★★☆☆ | ★★★★☆ |
| 夜深人静写算法(三十四)- 逆元 | ★★★☆☆ | ★★★★☆ |
| 夜深人静写算法(三十五)- RSA 加密解密 | ★★★☆☆ | ★★★★★ |
| 夜深人静写算法(三十六)- 中国剩余定理 | ★★☆☆☆ | ★★★☆☆ |
| 夜深人静写算法(三十七)- 威尔逊定理 | ★★☆☆☆ | ★★★☆☆ |
| 夜深人静写算法(三十八)- 整数分块 | ★★☆☆☆ | ★★★★☆ |
| 卢卡斯定理 | 待更新 | … |
| 狄利克雷卷积 | 待更新 | … |
| 莫比乌斯反演 | 待更新 | … |
| 容斥原理 | 待更新 | … |
| 拉宾米勒 | 待更新 | … |
| Pollard rho | 待更新 | … |
| 莫队 | 待更新 | … |
| 原根 | 待更新 | … |
| 大步小步算法 | 待更新 | … |
| 二次剩余 | 待更新 | … |
| 矩阵二分快速幂 | 待更新 | … |
| Polya环形计数 | 待更新 | … |
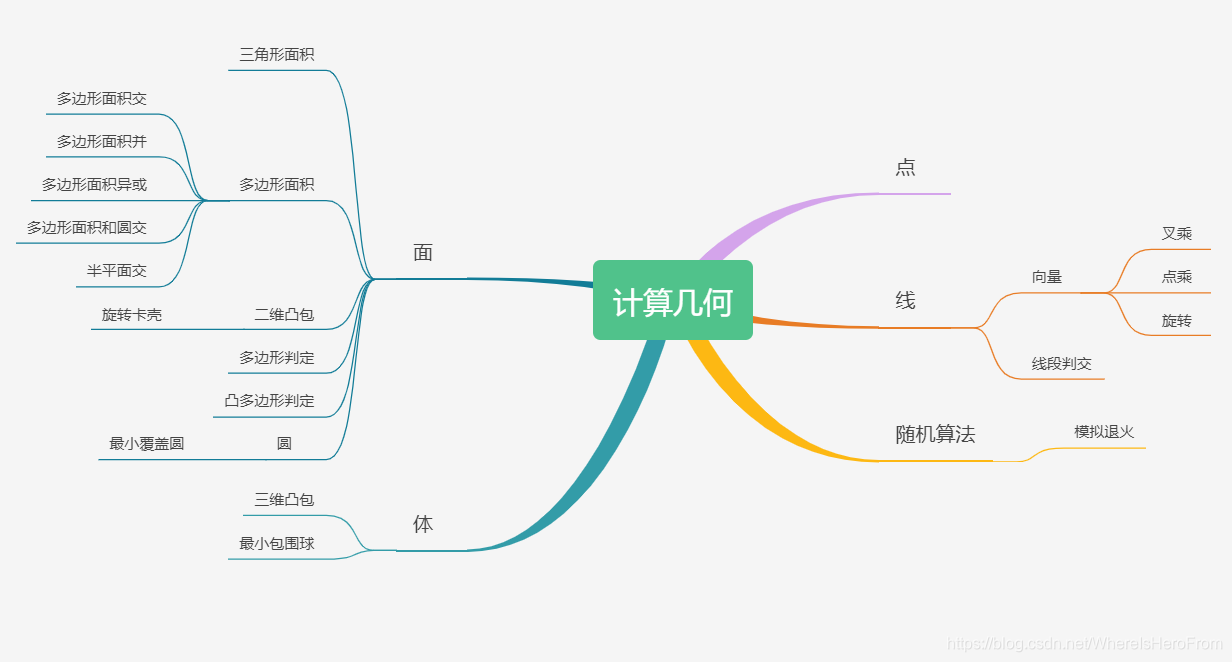
🛑4、进阶计算几何
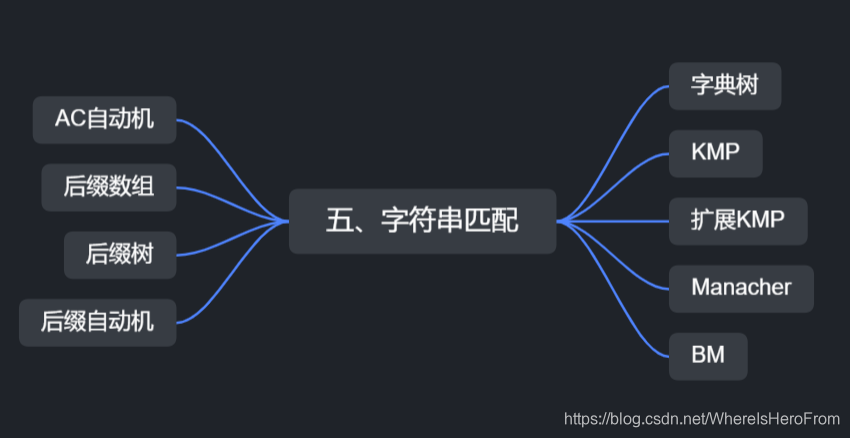
📏5、字符串的匹配
🎄6、高級数据结构
🙉饭不食,水不饮,题必须刷🙉
C语言免费动漫教程,和我一起打卡! 🌞《光天化日学C语言》🌞
LeetCode 太难?先看简单题! 🧡《C语言入门100例》🧡
数据结构难?不存在的! 🌳《画解数据结构》🌳
LeetCode 太简单?算法学起来! 🌌《夜深人静写算法》🌌