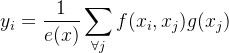1. WHY
问题
图像超分辨率一直是一个热门研究课题,具有重要的应用价值。基于生成对抗网络GAN的单幅图像超分辨率方法显示重建图像与人类视觉特征更一致。因此,基于 GAN 的网络优化已成为图像超分辨率的主流。然而,一些最新研究表明,基于GAN的图像超分辨率方法会导致结构失真。
结构失真
含义:结构失真指的是在使用某些图像超分辨率方法时,生成的高分辨率图像虽然分辨率提高了,但是图像中的物体结构发生了不应该有的变形、扭曲或者模糊等问题,导致图像看起来不自然,甚至影响对图像内容的准确理解。
产生原因:以基于 GAN 的图像超分辨率方法为例,常见的图像级生成对抗训练方式只是对整个图像进行二分类判断真假,没有考虑图像内部每个像素或者局部区域的结构关系。这就好比只看整栋房子的外观是否好看,却不关心房子内部的墙壁是否歪了、门窗是否变形。在这种情况下,生成的图像可能会出现局部结构混乱,比如原本是圆形的物体变成了椭圆形,直线变得弯曲,物体的边缘变得模糊不清等问题,使得图像的结构信息与原始图像相比出现了偏差和错误,也就是产生了结构失真。
现有方法
通过增强结构生成来缓解结构失真问题。但这种方法无法从根本上解决对抗训练导致的结构失真问题。
增强结构生成
含义:在图像超分辨率技术中,增强结构生成就是采取一系列措施,让生成的高分辨率图像能够更好地保留或恢复出原始低分辨率图像中物体的形状、轮廓、纹理等结构信息,使图像看起来更清晰、自然,接近真实的高分辨率图像。
方法举例:比如有些方法会专门设计一个独立的分支来生成高分辨率图像的梯度图(GM),这个梯度图就像是图像结构的一种指引。通过这个梯度图来指导整个超分辨率的过程,让生成的图像在细节和结构上更合理。就好像盖房子时,先有一个建筑结构的蓝图,然后按照这个蓝图来施工,确保房子的结构稳固、布局合理。在图像超分辨率里,这个梯度图就是那个 “蓝图”,引导着生成图像的结构朝着更好的方向发展。
于是本文提出了像素级生成对抗训练来解决结构失真问题,该方法在对抗训练过程中细致地约束图像的结构。此外,为了更好地生成图像的结构和细节,并充分利用图像中的相似纹理细节,我们构建了一个结构感知的图像超分辨率网络,该网络不仅通过梯度引导增强结构生成,还以多层次的方式有效整合非局部自相似模块。
2. WHAT
2.1. 结构感知DN
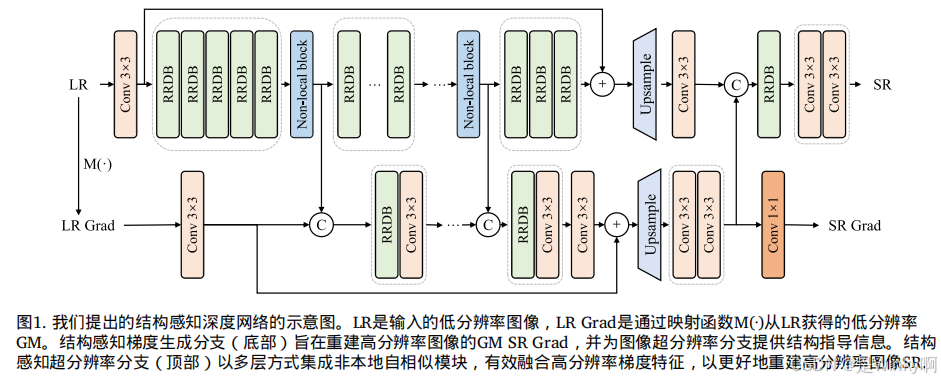
这个网络就像是一个智能的图像加工厂,有两个重要的 “车间”:一个是结构感知梯度生成分支,另一个是结构感知超分辨率分支。
梯度生成分支就像是一个 “结构分析员”,它会仔细研究低分辨率图像的梯度图(GM),这个 GM 就像是图像的 “结构草图”,包含了图像中物体的形状、边缘等结构信息。它还会结合超分辨率分支的各种特征信息,然后精心绘制出高分辨率图像的 GM,为超分辨率分支提供一个精确的 “结构蓝图”。
超分辨率分支则像是一群 “巧匠”,它们根据这个 “蓝图”,利用一种特殊的非局部自相似性模块,这个模块可以让图像中的各个部分互相参考、学习,就像工匠们互相交流经验一样,从而更好地理解图像的整体结构,进而生成高质量的高分辨率图像,让图像的细节更加丰富、清晰。
首先,在结构感知非局部自相似性模块中,有一套独特的计算方法来衡量图像中不同位置特征的相似性,就像在人群中找到志同道合的伙伴一样,把相似的特征联系起来,然后通过学习这些相似特征来优化图像的结构。
接着,结构感知梯度生成分支利用巧妙的计算方式从低分辨率图像中提取出 GM,再结合超分辨率分支的信息,经过一系列复杂的操作,如卷积、融合、上采样等,就像精心雕琢一件艺术品一样,逐步构建出高分辨率图像的 GM。
最后,结构感知超分辨率分支根据这个 GM,利用自身的网络结构和非局部自相似性模块,把低分辨率图像逐步提升为高质量的高分辨率图像,让图像的结构更加合理,细节更加逼真。
2.1.1. 非局部自相似模块
该模块基于独特的非局部均值操作定义,公式为
其中,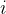
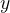
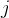
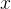
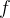
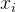
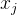
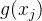
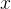
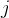
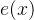
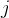
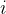
具体而言,函数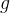
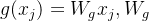
模块选用嵌入高斯函数作为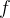
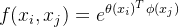
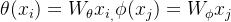
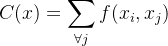
对于给定的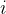
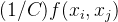
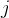
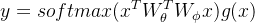
进一步引入残差学习思想,模块被公式化为为待学习参数。模块输入
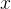
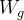
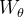
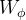
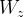
图 2. 非局部自相似性模块。特征图以其张量形状显示(在注明时进行适当的重塑)。“
” 表示矩阵乘法,“
” 表示逐元素求和。softmax 操作在每一行上执行。紫色框表示
卷积。
2.1.2. 梯度生成分支
该分支主要任务是从低分辨率输入图像的 GM 重建目标高分辨率图像的 GM。首先,通过映射函数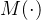
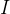
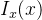
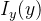
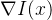
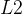
提取的低分辨率 GM 随后被送入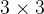
在 CONCAT 融合层之后,依次经过 RRDB 模块和卷积层的处理,此融合操作连续进行四次,然后通过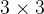
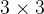
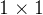
2.1.3. 超分辨率分支
基于现有研究成果,充分利用图像先验有助于提升图像超分辨率性能。尽管深度网络的感受野较大,但传统卷积网络在维持长程依赖方面仍存在不足。因此,本 SR 分支以多级方式集成非局部自相似性模块,旨在有效建立长程依赖关系,强化结构保留能力。同时,为生成更合理的图像结构和纹理,该分支进一步融合 GB 提供的结构信息。
具体操作流程为,分支首先使用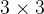
2.2. 像素级GAN
像素级生成对抗训练的目的是让生成的图像在结构上更加合理,避免出现结构失真的问题。它的做法是让生成器和判别器进行一场激烈的 “博弈”。判别器就像一个非常严格的 “裁判”,它会仔细检查生成图像的每个像素,判断这个像素是否和真实图像中的像素来自同一个分布,就像检查每个产品的零部件是否合格一样。生成器则像是一个 “生产者”,它根据低分辨率图像努力生成高分辨率图像,并且要尽量让判别器认为它生成的像素是真实的。
与传统的图像级对抗训练不同,传统的方法只是对整个图像进行一个大致的真假判断,就像只看一眼整栋房子的外观就判断好坏,而像素级生成对抗训练是深入到每个像素层面进行判断和优化。它通过构建一个特殊的基于全卷积的判别器,这个判别器可以输出一个和输入图像大小相同的概率图,每个像素都有对应的概率值,表示这个像素是真实像素的可能性。这样就能更精准地控制图像的结构生成,避免出现局部结构混乱的情况,使生成的图像更加自然、真实,就像精心打造每一个细节,让整栋房子从里到外都完美无缺。
2.2.1. 像素级对抗损失
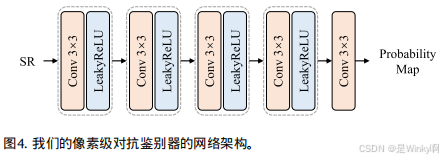
与图像级对抗判别器输出一个概率值来判定整个图像真假不同,像素级对抗判别器的输出是一个与输入图像大小相同的概率图,用于确定每个像素是否为真实像素。为此构建了一个基于全卷积的判别器,它由五个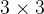
2.2.2. 梯度+图像联合优化损失
图像损失
以低分辨率(LR)图像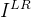
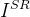
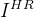
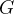
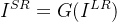
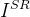
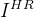
多数方法使用像素级重建损失优化网络:
如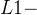
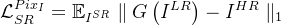
因此还使用 Johnson 等提出的感知损失函数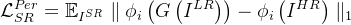
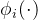
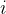
此外,超分辨率分支的像素级对抗损失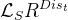
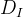
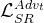
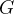
梯度损失
梯度图 (GM) 能反映图像结构信息,可作为生成器的二阶约束。
通过最小化从SR 图像和 HR 图像中提取的 GM 差异来实现梯度损失,包括:
基于像素级的损失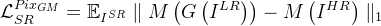
判别梯度像素是否来自HRGM的损失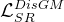
以及梯度判别器通过对抗学习对 SR 结果生成的监督损失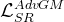
联合损失
判别器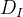
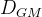
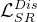
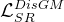
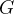
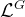
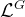
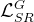
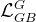
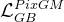
2.3. 实验
2.3.1. 训练细节
训练集:选用 DIV2K 数据集中编号从 0001 到 0800 的 800 张图像,将每张图像切割成 40 张小图像(每张 480×480 像素),共生成 32208 张作为目标高分辨率图像,通过双三次插值获得低分辨率输入,实验仅考虑 4 倍缩放因子。
测试集:使用 Set5、Set14、BSD100、Urban100 和 General100 五个常用数据集,所有数据集均使用双三次插值生成低高分辨率图像对,且训练集和测试集不同。
模型训练的超参数: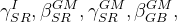
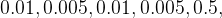
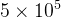
学习率的设置:采用了动态调整策略,随着训练送代次数的增加而逐渐递减。具体而言,在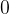
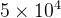
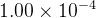
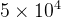
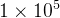
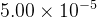
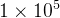
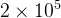
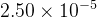
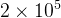
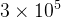
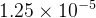
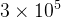
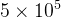
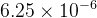
2.3.2. 非局部自相似性模块的影响
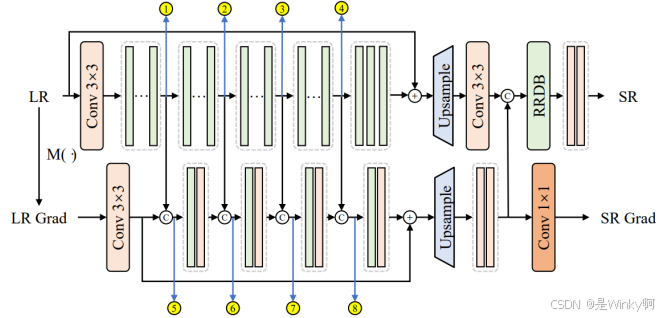
为深入探究非局部自相似性模块在网络中的作用,进行了一系列消融实验。具体而言,在 SPSR 网络的八个不同位置嵌入非局部自相似性模块,研究其在不同位置对网络性能的影响。这些候选嵌入位置分布在超分辨率分支(每 5 个 RRDB 模块后)和梯度生成分支(每个 concat 操作后),如图 14 所示。通过设计六个不同的消融实验(Exp.1 - Exp.6),分别在不同的组合位置嵌入非局部自相似性模块,并在相同的训练设置下(均训练 200000 次迭代)对各实验结果进行评估。实验结果以表格形式呈现(如表四所示),从中可以看出,并非在所有位置嵌入非局部自相似性模块都能带来性能提升,这表明在超分辨率网络中有效地融合非局部自相似性模块并非易事,需要精心选择嵌入位置。其中,Exp.5 的实验结果表明,当在超分辨率分支的特定位置(①、②、③、④)以多级方式嵌入非局部自相似性模块时,网络能够获得最佳的性能表现,在平均 PSNR 和 SSIM 指标上取得了较好的成绩。基于此实验结果,最终确定的结构感知深度网络仅在超分辨率分支的多个层级(①、②、③、④位置)嵌入四个非局部自相似性模块,以充分发挥其提升图像超分辨率性能的作用。
图 14. 非局部自相似性模块的八个候选嵌入位置示意图。
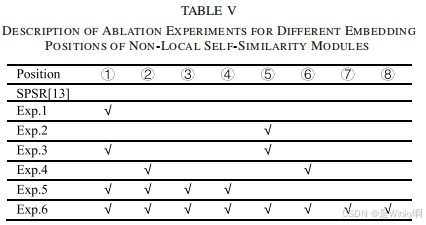
表四:非局部自相似性模块在不同嵌入位置的消融实验的平均 PSNR(峰值信噪比)和 SSIM(结构相似性)比较。最佳性能以粗体突出显示
表五:非局部自相似性模块不同嵌入位置的消融实验描述
2.3.3. 像素级生成对抗训练的影响
为了验证像素级生成对抗训练对图像超分辨率的影响,专门设计了对比实验。将像素级对抗训练直接应用于 SPSR 方法(记为 Exp.7),并将其结果与同时使用非局部自相似性模块和像素级对抗训练的 PGAN 方法进行对比。所有实验均在相同的训练条件下进行,训练次数为 500000 次迭代。实验结果以表格形式展示(如表六和表七所示),通过对比平均 PSNR 和 SSIM 指标可以发现,像素级对抗训练的引入显著提升了网络性能。在 SPSR 方法中加入像素级对抗训练后(Exp.7),其 PSNR 和 SSIM 值均有明显提高,这表明像素级对抗训练能够使网络生成的图像在结构和质量上更接近真实高分辨率图像。而 PGAN 方法在融合了多级非局部自相似性模块和像素级对抗训练后,进一步提升了性能,在定量指标上取得了最佳成绩。此外,通过视觉对比(如图 15 所示),可以直观地看到像素级对抗训练在缓解结构失真问题上的显著效果。在与图像级对抗训练(如 SPSR)的对比中,像素级对抗训练生成的图像结构更加合理,有效地减少了结构扭曲和变形等问题,使得图像看起来更加自然逼真。这充分证明了像素级生成对抗训练在提高图像超分辨率质量方面的重要作用,与结构感知深度网络相结合,能够为图像超分辨率任务提供更有效的解决方案。
表六:针对有和无非局部自相似性模块以及像素级对抗训练的网络的消融实验说明
表七:有和无非局部自相似性模块以及像素级对抗训练的图像超分辨率网络的平均PSNR(峰值信噪比)和SSIM(结构相似性)比较。最佳性能以粗体突出显示。
3. HOW
3.1. 定量对比
将提出的方法 PGAN 与基于 GAN 的图像超分辨率方法(SFTGAN、SRGAN、ESRGAN、NatSR、SPSR)进行对比。在五个数据集上的平均峰值信噪比(PSNR)、结构相似性(SSIM)、感知指数(PI)和学习感知图像块相似性(LPIPS)对比结果显示,PGAN 在大多数数据集上实现了最佳的平均 PSNR、SSIM 和 LPIPS 值,PI 值也与现有技术相当。
表一:各种基于 GAN 的先进图像超分辨率方法在五个数据集上的平均 PSNR 和 SSIM 比较。最佳性能以粗体突出显示
表二:各种基于 GAN 的先进图像超分辨率方法在五个数据集上的平均 PI(感知指数)和 LPIPS(学习感知图像块相似性)比较。最佳性能以粗体突出显示
此外,通过与基线 SPSR 在不同数据集上的测试时间对比,可以发现 PGAN 在运行速度上与 SPSR 相近,这意味着 PGAN 在实现高质量图像超分辨率的同时,并没有牺牲过多的计算效率。
表三:我们的方法 PGAN 与基线 SPSR 在不同数据集上的测试时间(以秒为单位)比较
进一步对比 PGAN 和 SPSR 在训练过程中的 PSNR 变化,可以清晰地看到 PGAN 的收敛速度更快,这表明 PGAN 在训练过程中能够更有效地优化模型参数,更快地达到较好的性能状态。
图 13. SPSR 与我们的 PGAN 在训练过程中的 PSNR(峰值信噪比)比较。
3.2. 定性对比
通过视觉效果对比,双三次插值结果模糊但无结构失真,SPSR 结果虽清晰但仍有结构失真问题,而 PGAN 结果更自然逼真,重建图像结构清晰,无失真和伪影,表明提出的方法可缓解 GAN - 基于方法的结构失真问题,提高重建图像的视觉感知效果。