前置芝士

并查集

引入

来看一道例题：

在一条数轴上有 $n$ 个点，分别为 $1\sim n$。一开始所有的点都被染成黑色。接着进行 $m$ 次操作，第 $i$ 次操作将 $[l,r]$ 这些点染成白色。请输出每个操作执行后剩余黑色点的个数。

暴力？嗯。。。直接T飞

我们要用并查集！

实现

这题看似与并查集毫无关联。但是，我们仔细推敲过后，发现：

还是毫无关联

好吧，我们来模拟一下暴力的过程。

初始时是这样的：（为了便于表述，用格子代替点）

我们对$[4,5]$涂色：

对$[8,10]$涂色：

对$[5,8]$涂色：

等等，问题来了，我们发现，在区间$[5,8]$内，有已经涂好的。我们还要再涂一遍吗？可不可以标记出来呢？比如说，把白色格子直接指到黑色格子上？

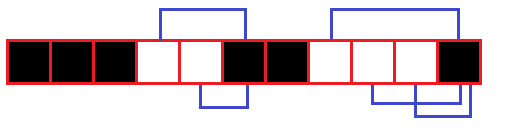
关键来了！指到！你想到了什么？并查集！我们可以使用并查集，把每个涂白的格子指到下一个涂黑的格子去！就像这样：

这样，我们每次涂色，可以直接跳到黑色格子里，而不用在白色格子上浪费时间。

完整代码

#include<iostream>
#include<cstdio>
using namespace std;
int n,m,l,r,ans;
int f[1000010];
int root(int x)
{
	if(f[x]==x)
		return x;
	f[x]=root(f[x]);
	return f[x];
}
void join(int x,int y)
{
	int r1=root(x),r2=root(y);
	if(r1!=r2)
		f[r1]=r2;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n+1;i++)
		f[i]=i;
	ans=n;
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d",&l,&r);
		int r1=root(l);
		while(r1<=r)
		{
			join(r1,r1+1);
			r1=root(r1);
			ans--;
		}
		printf("%d\n",ans);
	}
	return 0;
}

升级版——多种颜色

洛谷 P2391 白雪皑皑

现在有 $n$ 片雪花排成一列。 pty 要对雪花进行 $m$ 次染色操作，第 $i$ 次染色操作中，把第 $((i\times p+q)\mathrm{m}\mathrm{o}\mathrm{d}n)+1$ 片雪花和第 $((i\times q+p)\mathrm{m}\mathrm{o}\mathrm{d}n)+1$ 片雪花之间的雪花（包括端点）染成颜色 $i$。其中 $p,q$ 是给定的两个正整数。他想知道最后 $n$ 片雪花被染成了什么颜色。没有被染色输出 $0$。

看来，这一次，我们不能把染过的格子跳过去了，因为颜色可能会覆盖，每个格子的颜色都是它们最后一次染的颜色。。。

最后一次？最后一次！我们可以倒着染！然后将染到的颜色记录即可。

#include<iostream>
#include<cstdio>
using namespace std;
int n,m,p,q;
int l,r,r1;
int f[1000010];
int ans[1000010];
int root(int x)
{
	if(f[x]==x)
		return x;
	f[x]=root(f[x]);
	return f[x];
}
void join(int x,int y)
{
	int r1=root(x),r2=root(y);
	if(r1!=r2)
		f[r1]=r2;
}
int main()
{
	scanf("%d%d%d%d",&n,&m,&p,&q);
	for(int i=1;i<=n+1;i++)
		f[i]=i;
	for(int i=m;i>=1;i--)
	{
		l=(i*p+q)%n+1;
		r=(i*q+p)%n+1;
		if(l>r)
			swap(l,r);
		r1=root(l);
		while(r1<=r)
		{
			ans[r1]=i;
			join(r1,r1+1);
			r1=root(r1+1);
		}
	}
	for(int i=1;i<=n;i++)
		printf("%d\n",ans[i]);
	return 0;
}