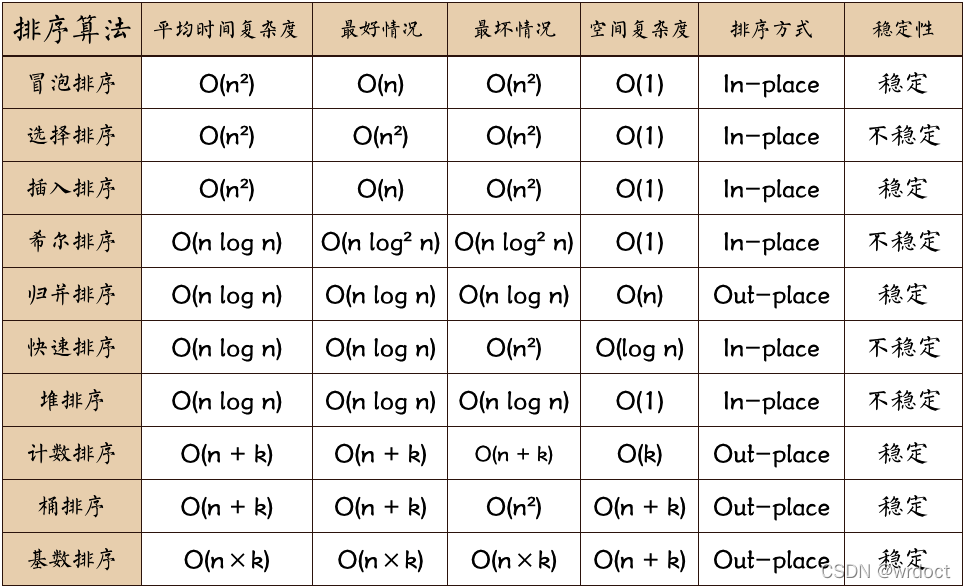
稳定排序(排序前后两个相等的数的相对位置不变):归并排序、冒泡排序、插入排序、基数排序;
非稳定排序:希尔排序、堆排序、选择排序、快速排序。
1.快速排序
快速排序采用分而治之的思想,选取基准值,第一次排序之后将小于等于基准值的值都放在该值前面,将大于等于基准值的值都放在该值后面,接下来对前面的和后面的再次进行快速排序,分而治之直到无法再“分”为止。
#include <iostream>
#include <vector>
#include <string>
#include <fstream>
using namespace std;
int Paritition(vector<int> &array, int left, int right) {
int tmp = array[left];//选取一个基准值
while (left < right) {
while (left < right && tmp <= array[right]) {
right--;//基准值小于等于后面的值 右指针左移
}
if (left < right) array[left++] = array[right]; //将后边小于基准值的值放在前面,左指针右移
while (left < right && tmp > array[left]) {
left++;//基准值大于后面的值 左指针右移
}
if (left < right) array[right--] = array[left];//将前面大于等于基准值的值放在后面,右指针左移
}
array[left] = tmp;//左右指针重合 存入基准值
return left; //此时left的前面值都小于基准值, 后面的值都大于基准值
}
void QuickSort(vector<int> &array, int &left, int &right) {
if (left >= right) return;
//分而治之
int mid = Paritition(array, left, right);//分为两部分
QuickSort(array, left, mid - 1);//前半部分
QuickSort(array, mid + 1, right);//后半部分
}
int main(int argc, char* argv[]) {
vector<int> array;
int num;
while (1) {
cin >> num;
array.push_back(num);
if (cin.get() == '\n') break;
}
int left = 0, right = array.size() - 1;
QuickSort(array, left, right);//快速排序函数
for (int i = 0; i < array.size(); i++) {
cout << array[i] << " ";
}
return -1;
}
//优化快速排序
以下代码有三种快速排序的写法,参考STL标准模板库对快速排序进行优化
#include <iostream>
#include <vector>
#include <string>
#include <fstream>
#include <algorithm>
using namespace std;
/**************************快排一********************/
void QuickSort_v1(vector<int> &array, int l, int r) {
if (l >= r) return;
int x = l, y = r, z = array[l];
while (x < y) {
while (x < y && array[y] >= z) --y;
if (x < y) array[x++] = array[y];
while (x < y && array[x] <= z) ++x;
if (x < y) array[y--] = array[x];
}
array[x] = z;
QuickSort_v1(array, x + 1, r);
QuickSort_v1(array, l, x - 1);
return;
}
/**************************优化——快排二********************/
#define Swap(a, b) { \
auto _a = a; \
a = b, b = _a; \
}
//三点取中法
inline int midian(int a, int b, int c) {
if (a > b) Swap(a, b);
if (a > c) Swap(a, c);
if (b > c) Swap(b, c);
return b;
}
void QuickSort_v2(vector<int> &array, int l, int r) {
while (l < r) {
int x = l, y = r, z = midian(array[l], array[(l + r) >> 1], array[r]);
//无监督
do {
while (array[x] < z) ++x;
while (array[y] > z) --y;
if (x <= y) {
Swap(array[x], array[y]);
++x, --y;
}
} while (x <= y);
QuickSort_v2(array, x, r);
r = y; //单边递归
}
return;
}
/**************************优化——快排三********************/
const int threshold = 16;
void _QuickSort_v3(vector<int> &arr, int l, int r) {
while (r - l > threshold) {
int x = l, y = r, z = midian(arr[l], arr[(l + r) >> 1], arr[r]);
//无监督
do {
while (arr[x] < z) ++x;
while (arr[y] > z) --y;
if (x <= y) {
Swap(arr[x], arr[y]);
++x, --y;
}
} while (x <= y);
_QuickSort_v3(arr, x, r);
r = y;//单边递归
}
return;
}
void InsertSort(vector<int> &arr, int l, int r) {
int ind = l;
for (int i = l + 1; i <= r; i++) {
if (arr[ind] > arr[i]) ind = i;
}
Swap(arr[ind], arr[l]);
for (int i = l + 2; i <= r; i++) {
int j = i;
while (arr[j] < arr[j - 1]) {
Swap(arr[j], arr[j - 1]);
--j;
}
}
return;
}
void QuickSort_v3(vector<int> &arr, int l, int r) {
_QuickSort_v3(arr, l, r);//数组大小超过16使用快速排序
InsertSort(arr, l, r); //小于16用插入排序
return;
}
int main(int argc, char* argv[]) {
vector<int> array;
int num;
while (1) {
cin >> num;
array.push_back(num);
if (cin.get() == '\n') break;
}
//QuickSort_v1(array, 0, array.size() - 1);
//QuickSort_v2(array, 0, array.size() - 1);
QuickSort_v3(array, 0, array.size() - 1);
for (int i = 0; i < array.size(); i++) {
cout << array[i] << " ";
}
return -1;
}
2.插入排序
在快速排序中第三个版本已使用。
先选定第一个值为最小(第一个for循环),之后从下一位开始进行比较填充,每次保证从第一位到第j位有序(for循环中使用while循环)
void InsertSort(vector<int> &arr, int l, int r) {
int ind = l;
for (int i = l + 1; i <= r; i++) {
if (arr[ind] > arr[i]) ind = i;
}
Swap(arr[ind], arr[l]);
for (int i = l + 2; i <= r; i++) {
int j = i;
while (arr[j] < arr[j - 1]) {
Swap(arr[j], arr[j - 1]);
--j;
}
}
return;
}
3.选择排序
每次选中一个值,将该值与后面所有的值进行比较,最终给每个位置选择当前元素最小的值。
#include <iostream>
#include <vector>
#include <string>
#include <fstream>
#include <algorithm>
using namespace std;
void Swap(vector<int>& array, int i, int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
void SelectSort(vector<int>& array) {
if (array.size() < 2) return;
for (int i = 0; i < array.size() - 1; i++) {
int minCur = i;
for (int j = i + 1; j < array.size(); j++) {
minCur = array[j] < array[minCur] ? j : minCur;
}
Swap(array, i, minCur);
}
}
int main(int argc, char* argv[]) {
vector<int> array;
int num;
while (1) {
cin >> num;
array.push_back(num);
if (cin.get() == '\n') break;
}
SelectSort(array);
for (int i = 0; i < array.size(); i++) {
cout << array[i] << " ";
}
return -1;
}
4.冒泡排序
重复地遍历要排序的数列,每次比较相邻的两个元素,如果它们的顺序错误就把它们交换过来,这样在最后的元素应该会是最大的数。
#include <iostream>
#include <vector>
#include <string>
#include <fstream>
#include <algorithm>
using namespace std;
void Swap(vector<int>& array, int i, int j) {
array[i] = array[i] ^ array[j];
array[j] = array[i] ^ array[j];
array[i] = array[i] ^ array[j];
/*int tmp = array[i];
array[i] = array[j];
array[j] = tmp;*/
}
void BubbleSort(vector<int>& array) {
if (array.size() < 2) return;
for (int i = 0; i < array.size(); i++) {
for (int j = 0; j < array.size() - i - 1; j++) {
if (array[j] > array[j + 1]) {
Swap(array, j, j + 1); //在最后的元素应该会是最大的数
}
}
}
}
int main(int argc, char* argv[]) {
vector<int> array;
int num;
while (1) {
cin >> num;
array.push_back(num);
if (cin.get() == '\n') break;
}
BubbleSort(array);
for (int i = 0; i < array.size(); i++) {
cout << array[i] << " ";
}
return -1;
}
5.归并排序
求出中点位置,先让左侧排好序,再让右边排好序(分而治之),之后往一块整合(类似合并两个有序数组),整合到辅助数组里,之后再整体放回原数组。
可以用来解决“逆序对”系列问题。
#include <iostream>
#include <vector>
#include <string>
#include <fstream>
#include <algorithm>
using namespace std;
void merge(vector<int>& arr, int l, int mid, int r) {
vector<int> help;// (r - l + 1, 0); //每次递归都会是一个新的help数组
int p1 = l;
int p2 = mid + 1;
int tmp = 0;
while (p1 <= mid || p2 <= r) {
if (p1 == mid + 1) {//越界
tmp = arr[p2++];
}
else if (p2 == r + 1) { //越界
tmp = arr[p1++];
}
else if(arr[p1] < arr[p2]){
tmp = arr[p1++];
}
else{
tmp = arr[p2++];
}
help.push_back(tmp);
}
for (int i = 0; i < help.size(); i++) {
arr[l + i] = help[i];//但是arr不是新的数组
}
return;
}
void MergeSort(vector<int>& arr, int l, int r) {
if (l == r) return;
int mid = l + ((r - l) >> 1);
MergeSort(arr, l, mid);
MergeSort(arr, mid + 1, r);
merge(arr, l, mid, r);
return;
}
int main(int argc, char* argv[]) {
vector<int> arr;
int num;
while (1) {
cin >> num;
arr.push_back(num);
if (cin.get() == '\n') break;
}
MergeSort(arr, 0, arr.size() - 1);
for (int i = 0; i < arr.size(); i++) {
cout << arr[i] << " ";
}
return -1;
}
6.堆排序
堆是一个近似完全二叉树的结构,并同时满足堆的性质:即子结点的键值或索引总是小于(小根堆)(或者大于(大根堆))它的父节点。
先将第一位变为整个数组大根堆的父节点,再将最后一个数和第一个数做交换,这样可确保最大值在最后一位,然后整个数组大小(heapSize)减一(将最后一位“断联”)。
之后从第0位往下判断是否还能下移,以确保前面的数组依然为大根堆,之后交换,heapSize减一。知道heapSize为0,排序完成。
#include <iostream>
#include <vector>
#include <string>
#include <fstream>
#include <algorithm>
using namespace std;
//左子节点:2*i+1
//右子节点:2*i+2
//父节点:(i-1)/2
#define Swap(a, b) { \
auto _a = a; \
a = b, b = _a; \
}
//堆插入
void HeapInsert(vector<int>& arr, int idx) {
while (arr[idx] > arr[(idx - 1) / 2]) { //当前值和父的值作比较 看能否上移
Swap(arr[idx], arr[(idx - 1) / 2]);
idx = (idx - 1) / 2; //
}
}
//某个数在idx位置(看作父位置),能否往下移动
void HeapIfy(vector<int>& arr, int idx, int heapSize) {
int left = idx * 2 + 1; //左孩子的下标
while (left < heapSize) { //下方还有孩子
//两个孩子中,谁的值大,把下标给largest
int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
//父和较大的孩子之间,谁的值大,把下标给largest
largest = arr[largest] > arr[idx] ? largest : idx;
if (largest == idx) { //最大值就是当前父位置
break;
}
Swap(arr[largest], arr[idx]);
idx = largest; //索引值的变化
left = idx * 2 + 1; //
}
}
void HeapSort(vector<int>& arr) {
if (arr.empty() || arr.size() < 2) {
return;
}
//把数组整体范围全变成大根堆
/*for (int i = 0; i < arr.size(); i++) {
HeapInsert(arr, i); //O(logN) //这时只能保证首位值最大,其他只是满足大根堆 不一定有序
}*/
//效率更高的办法
for (int i = arr.size() - 1; i >= 0; i--) {
HeapIfy(arr, i, arr.size());
}
int heapSize = arr.size();
Swap(arr[0], arr[heapSize - 1]); //首位和最后一位做交换,此时最后一位必是最大值
heapSize--; //最后一位“断联”
while (heapSize > 0) {
HeapIfy(arr, 0, heapSize);
Swap(arr[0], arr[heapSize - 1]);
heapSize--; //最后一位“断联”
}
}
int main(int argc, char* argv[]) {
vector<int> arr;
int num;
while (1) {
cin >> num;
arr.push_back(num);
if (cin.get() == '\n') break;
}
HeapSort(arr);
for (int i = 0; i < arr.size(); i++) {
cout << arr[i] << " ";
}
return -1;
}
7.计数排序
计数排序 的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
8.桶排序
桶排序 是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。
假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序。
9.基数排序
对每一位进行排序,从最低位开始排序。按照低位先排序,然后收集(根据count前缀和数组存入help数组);再按照高位排序,然后再收集;依次类推,直到最高位。(也可认为是优先级低的先排序,高优先级的再排序)。
即先根据个位数字排序,再根据十位数字排序,再根据百位数字排序…
#include <iostream>
#include <vector>
#include <string>
#include <fstream>
#include <algorithm>
using namespace std;
//最大值有几个十进制位
int maxbits(vector<int>& arr) {
int _max = INT_MIN;
for (int i = 0; i < arr.size(); i++) {
_max = max(_max, arr[i]);
}
int res = 0;
while (_max |= 0) {
res++;
_max /= 10;
}
return res;
}
//将x的第d位的数字拿出来
int GetDigit(int x, int d) {
for (int i = 1; i < d; i++) { //d >= 1
x /= 10;
}
x %= 10;
return x;
}
//在left到right范围内排序
void _RadixSort(vector<int>& arr, const int left, const int right, int digit) {
const int radix = 10; //"前缀和"的最大空间
vector<int> help(right - left + 1);
int i = 0;
for (int d = 1; d <= digit; d++) { //入桶出桶的次数 //最大值的位数 //排序的次数
int count[radix] = { 0 }; // //count[1]表示当前位是0和1的数字有多少个(小于等于1的个数)
for (i = left; i <= right; i++) {
int j = GetDigit(arr[i], d); //依次拿出arr数组中每个数 第d位上 值为j的总个数 (d = 1是个位)
count[j]++; //个数放进count数组中
}
for (i = 1; i < radix; i++) {
count[i] += count[i - 1]; //处理成前缀和
}
//数组从右往左遍历
for (i = right; i >= left; i--) {
int j = GetDigit(arr[i], d); //拿出位数
help[count[j] - 1] = arr[i]; //填进辅助数组
count[j]--; //前缀和那个词频(个数) 减一
}
//维护本次出桶的结果再放回arr
for (i = left; i <= right; i++) { //
arr[i] = help[i]; //
}
}
}
void RadixSort(vector<int>& arr) {
if (arr.empty() || arr.size() < 2) {
return;
}
_RadixSort(arr, 0, arr.size() - 1, maxbits(arr));
}
int main(int argc, char* argv[]) {
vector<int> arr;
int num;
while (1) {
cin >> num;
arr.push_back(num);
if (cin.get() == '\n') break;
}
RadixSort(arr);
for (int i = 0; i < arr.size(); i++) {
cout << arr[i] << " ";
}
return -1;
}
10.希尔排序
希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本。
11.补充
【注】可以使用系统自带的sort函数与自己写的排序函数进行对数器比对,以测试自己写的是否正确。
产生随机数进行测试并检查排序函数:
#define MAX_N 100
vector<int> arr;
void GetRandData(int n) {
for (int i = 0; i < n; i++) {
arr.push_back(rand() % n);
}
return;
}
int Check(vector<int> &arr, int n) {
for (int i = 1; i < n; i++) {
if (arr[i] < arr[i - 1]) return 0;
}
return 1;
}
int main(int argc, char* argv[]) {
vector<int> array;
srand(time(0));
GetRandData(MAX_N);
array = arr;
if (Check(array, MAX_N) == 1) {
cout << "排序正确" << endl;
}
return -1;
}