子图同构之VF2
1.子图同构问题描述
首先描述一下子图同构是什么意思,一个图由一系列节点和一系列连接节点的边构成,节点和边都可以有标签,也就是可以给他们按属性分类。
精确点:一个图 G = ( V , E ) G=(V,E) G=(V,E)由集合 V V V和集合 E E E组成, V V V是节点(node)集合, E E E是边(edge)集合,且 E ⊂ V × V E\subset V\times V E⊂V×V ,用 L v L_v Lv表示节点上的标签集合, L e L_e Le表示边上的标签集合,那么每个节点对应的标签由函数(或者说映射) λ v : V → L v \lambda_v:V\rightarrow L_v λv:V→Lv 确定,每条边对应的标签由函数 λ e : E → L e \lambda_e:E\rightarrow L_e λe:E→Le 确定。
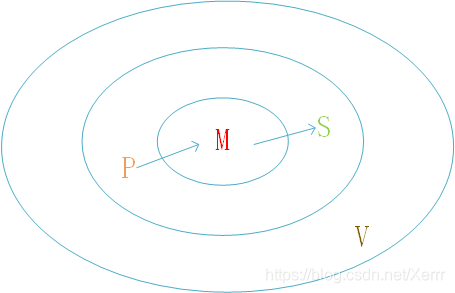
现在给定两个图 G 1 = ( V 1 , E 1 ) G_1=(V_1,E_1) G1=(V1,E1), G 2 = ( V 2 , E 2 ) G_2=(V_2,E_2) G2=(V2,E2) ,其中 G 1 G_1 G1是比较小的图(我们把它叫做pattern graph), G 2 G_2 G2是比较大的图(我们把它叫做target graph),用集合 M ⊂ V 1 × V 2 M\sub V_1\times V_2 M⊂V1×V2 表示两个图中节点的对应关系。如果节点 u ∈ V 1 u\in V_1 u∈V1,则 μ ( u ) ∈ V 2 \mu(u)\in V_2 μ(u)∈V2表示与节点 u u u对应的 G 2 G_2 G2中的节点;如果节点 v ∈ V 2 v\in V_2 v∈V2,则 ν ( v ) ∈ V 1 \nu(v)\in V_1 ν(v)∈V1表示与节点 v v v对应的 G 1 G_1 G1中的节点。
| G 1 G_1 G1 | G 2 G_2 G2 | |
|---|---|---|
| 对应关系 | u u u | μ ( u ) \mu(u) μ(u) |
| 对应关系 | μ − 1 ( v ) \mu^{-1} (v) μ−1(v) | v v v |
如果以下6个条件成立,则这两个图是子图同构的。
- ∀ u ∈ V 1 ∃ μ ( u ) ∈ V 2 : ( u , μ ( u ) ) ∈ M \forall u\in V_1 \quad \exist \mu(u)\in V_2:(u,\mu(u))\in M ∀u∈V1∃μ(u)∈V2:(u,μ(u))∈M
- ∀ u , u ′ ∈ V 1 u ≠ u ′ ⇒ μ ( u ) ≠ μ ( u ′ ) \forall u,u^{'}\in V_1 \quad u\neq u^{'}\Rightarrow \mu(u)\neq \mu(u^{'}) ∀u,u′∈V1u=u′⇒μ(u)=μ(u′)
- ∀ ( u , u ′ ) ∈ E 1 ∃ ( μ ( u ) , μ ( u ′ ) ) ∈ E 2 ) \forall (u,u^{'})\in E_1 \quad \exist (\mu(u),\mu(u^{'}))\in E_2) ∀(u,u′)∈E1∃(μ(u),μ(u′))∈E2)
- ∀ u , u ′ ∈ V 1 ( μ ( u ) , μ ( u ′ ) ) ∈ E 2 ⇒ ( u , u ′ ) ∈ E 1 \forall u,u^{'} \in V_1 \quad (\mu(u),\mu(u^{'})) \in E_2 \Rightarrow (u,u^{'}) \in E_1 ∀u,u′∈V1(μ(u),μ(u′))∈E2⇒(u,u′)∈E1
- ∀ u ∈ V 1 λ V 1 ( u ) = λ V 2 ( μ ( u ) ) \forall u \in V_1 \quad \lambda_{V_1}(u)=\lambda_{V_2}(\mu(u)) ∀u∈V1λV1(u)=λV2(μ(u))
- ∀ ( u , u ′ ) ∈ E 1 λ e 1 ( u , u ′ ) = λ e 2 ( μ ( u ) , μ ( u ′ ) ) \forall (u,u^{'}) \in E_1 \quad \lambda_{e_1}(u,u^{'})=\lambda_{e_2}(\mu(u),\mu(u^{'})) ∀(u,u′)∈E1λe1(u,u′)=λe2(μ(u),μ(u′))
用人话来解释一下:
-
对于小图中每个节点,大图中都要有一个对应的节点与之对应,并且这样一对一对的节点构成了集合 M M M;
-
小图中任意两个不一样的节点,他们对应的大图中的节点不能是同一个;
-
小图中每条边,大图中都有一条边与之对应,并且他们两端的节点一一对应;
-
小图中任意两个节点,如果他们对应的大图中的节点之间有一条边,那么小图中这两个节点之间也得有条边;
-
每对对应节点的label要相同,也就是这俩节点类型或属性相同;
-
每对对应边的label要相同,也就是说这俩边的类型或属性相同。
综上所述,子图同构简单来说就是,大图中有一个子结构,长得跟小图一模一样,而且这个子结构的节点之间不能多出小图中不存在的边来,如果要去掉最后这个而且,就把上面第4个条件去掉~
2.VF2算法
VF2算法的目标是,给定一个小图和一个大图,找出大图中所有与小图同构的子图,这是一个NP-hard问题。整体上,VF3算法是一个树搜索算法,并且想办法去尽可能剪枝。搜索树上的每个节点都是一个状态(state),记为 s s s,每个 s s s中包含一系列节点的映射关系,可以想象成一系列key-value对,key都是小图中的节点,value都是大图中的节点。搜索最开始的时候(也就是树的根节点) s s s中什么都没有,随着搜索的进行(树高度的增加), s s s中的key-value对会一对对增加,假如这个状态中所有的节点对都满足第一节中的6条约束,我们称这个状态为一致状态(consistent state);如果一个一致状态包含的小图中所有的节点,那意味着我们找到了一个大图的子结构与小图同构,称之为目标状态(goal state);如果一个状态是不可能再派生出一致状态的,我们称之为死亡状态(dead state)。
那么现在最大的问题就是两个:
- 这棵搜索树怎么组织?
- 怎么设计剪枝规则?
下面逐个展开~
A. 总体流程介绍
先来介绍一些符号:
M ~ ( s ) \tilde{M}(s) M~(s)表示状态 s s s中的节点映射集合,则 M ~ ( s ) ⊆ M \tilde{M}(s) \subseteq M M~(s)⊆M;
M 1 ~ ( s ) \tilde{M_1}(s) M1~(s)表示 M ~ ( s ) \tilde{M}(s) M~(s)中属于 G 1 G_1 G1的节点,也就是所有的key,严格点: M 1 ~ ( s ) = { u ∈ V 1 : ∃ ( u , v ) ∈ M ~ ( s ) , v ∈ V 2 } \tilde{M_1}(s)=\{u\in V_1:\exist (u,v)\in \tilde{M}(s),v\in V_2\} M1~(s)={u∈V1:∃(u,v)∈M~(s),v∈V2};
M 2 ~ ( s ) \tilde{M_2}(s) M2~(s)表示 M ~ ( s ) \tilde{M}(s) M~(s)中属于 G 2 G_2 G2的节点,也就是所有的value,严格点: M 2 ~ ( s ) = { v ∈ V 2 : ∃ ( u , v ) ∈ M ~ ( s ) , u ∈ V 1 } \tilde{M_2}(s)=\{v\in V_2:\exist (u,v)\in \tilde{M}(s),u\in V_1\} M2~(s)={v∈V2:∃(u,v)∈M~(s),u∈V1};
G ~ 1 ( s ) \tilde{G}_1(s) G~1(s)表示仅包含节点在 M 1 ~ ( s ) \tilde{M_1}(s) M1~(s)中的 G 1 G_1 G1的子图,也就是比 M 1 ~ ( s ) \tilde{M_1}(s) M1~(s)加上了边;
G ~ 2 ( s ) \tilde{G}_2(s) G~2(s)表示仅包含节点在 M 2 ~ ( s ) \tilde{M_2}(s) M2~(s)中的 G 2 G_2 G2的子图,也就是比 M 2 ~ ( s ) \tilde{M_2}(s) M2~(s)加上了边;
μ ~ ( s , u ) \tilde{\mu}(s,u) μ~(s,u)表示 M ~ ( s ) \tilde{M}(s) M~(s)中与 u u u对应的节点,其中 u ∈ V 1 u\in V_1 u∈V1, μ ~ ( s , u ) ∈ V 2 \tilde{\mu}(s,u)\in V_2 μ~(s,u)∈V2;
μ ~ − 1 ( s , v ) \tilde{\mu}^{-1}(s,v) μ~−1(s,v)表示 M ~ ( s ) \tilde{M}(s) M~(s)中与 v v v对应的节点,其中 μ ~ − 1 ( s , v ) ∈ V 1 \tilde{\mu}^{-1}(s,v)\in V_1 μ~−1(s,v)∈V1, v ∈ V 2 v\in V_2 v∈V2。
| V 1 V_1 V1 | V 2 V_2 V2 | |
|---|---|---|
| 对应关系 | u u u | μ ( s , u ) \mu(s,u) μ(s,u) |
| 对应关系 | μ − 1 ( s , v ) \mu^{-1} (s,v) μ−1(s,v) | v v v |
大致看一下整个流程,上伪代码~VF2总流程
1: f u n c t i o n V F 2 ( G 1 , G 2 ) function \ \ VF2(G_1,G_2) function VF2(G1,G2)
2: S o l u t i o n s = ∅ \ \ \ \ \ \ Solutions\ = \empty Solutions =∅
3: M ( s 0 ) = ∅ \ \ \ \ \ \ M(s_0)=\empty M(s0)=∅
4: M a t c h ( M ( s 0 ) , G 2 , G 1 , S o l u t i o n s ) \ \ \ \ \ \ Match(M(s_0),G_2,G_1,Solutions) Match(M(s0),G2,G1,Solutions)
5: r e t u r n S o l u t i o n s \ \ \ \ \ \ return \ \ Solutions return Solutions
1: f u n c t i o n M a t c h ( M ( s ) , G 2 , G 1 , S o l u t i o n s ) function \ \ Match(M(s),G_2,G_1,Solutions) function Match(M(s),G2,G1,Solutions)
2: i f M ( s ) c o v e r s a l l t h e n o d e s o f G 1 t h e n \ \ \ \ \ \ if\ \ M(s) \ \ covers\ \ all\ \ the\ \ nodes\ \ of \ \ G_1\ \ then if M(s) covers all the nodes of G1 then
3: A p p e n d ( M ( s ) , S o l u t i o n s ) \ \ \ \ \ \ \ \ \ \ \ \ Append(M(s),Solutions) Append(M(s),Solutions)
4: e l s e \ \ \ \ \ \ else else
5: P ( s ) = G e t C a n t i t a t e s ( M ( s ) ) \ \ \ \ \ \ \ \ \ \ \ \ P(s)=GetCantitates(M(s)) P(s)=GetCantitates(M(s))
6: f o r e a c h p a i r i n P ( s ) \ \ \ \ \ \ \ \ \ \ \ \ foreach\ \ pair\ \ in\ \ P(s) foreach pair in P(s)
7: i f I s F e a s i b l e ( p a i r ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ if\ \ IsFeasible(pair) if IsFeasible(pair)
8: M ( s ′ ) = E x t e n d M a t c h ( ( M ( s ) , p a i r ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ M(s^{'})=ExtendMatch((M(s),pair) M(s′)=ExtendMatch((M(s),pair)
9: M a t c h ( M ( s ′ ) , G 2 , G 1 , S o l u t i o n s ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Match(M(s^{'}),G_2,G_1,Solutions) Match(M(s′),G2,G1,Solutions)
10: B a c k T r a c k ( M ( s ′ ) , p a i r ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ BackTrack(M(s^{'}),pair) BackTrack(M(s′),pair)
一开始, M ~ ( s ) \tilde{M}(s) M~(s)中什么都没有,调用 M a t c h Match Match函数开始后,先根据当前状态 s s s和一些与 s s s中节点的连接拓扑关系,获得节点对集合 P ( s ) P(s) P(s),这是接下来准备加入状态 s s s候选节点对集合,每一节点对包含一个小图节点和一个大图节点。接下来对这个候选节点对集合遍历,每取出一对节点,先用 I s F e a s i b l e IsFeasible IsFeasible函数判断其是否可行,如果可以有一些规则提前知道,这一对节点加入必然不可能最终得到一对子图同构,就可以不继续往下搜索;如果该节点对可行,就将这对节点加入状态 s s s得到状态 s ′ s^{'} s′,并递归调用 M a t c h Match Match函数继续往下搜索。搜完每一分支进行回溯,整个过程就是一个深度优先搜索过程,状态 s s s构成了树的每一个节点, s s s中的节点数相当于搜索树的深度。每找到一个子图同构(也就是深度达到小图节点数)就把结果加入 S o l u t i o n Solution Solution。因此该算法的关键在于如何设计可行规则,尽可能早地筛除不可能最终获得子图同构的节点对,也就是尽可能早、尽可能多地砍掉搜索树中的分支。
B 候选节点对
首先我们将一个状态下不在 M ~ ( s ) \tilde M(s) M~(s)里的节点分为 P ~ 1 \tilde P_1 P~1, S ~ 1 \tilde S_1 S~1, V ~ 1 \tilde V_1 V~1 P ~ 2 \tilde P_2 P~2, S ~ 2 \tilde S_2 S~2, V ~ 2 \tilde V_2 V~2 ,其中下标1代表是属于小图 G 1 G_1 G1的节点子集,下标2代表是属于大图 G 2 G_2 G2的节点子集, P P P是predecessor,意思是前驱节点,具体讲是至少有一条边连接到已经匹配的 M ~ ( s ) \tilde M(s) M~(s)集合中节点的所有节点构成的集合,好拗口…重来:一个predecessor节点就是有边指向 M ~ ( s ) \tilde M(s) M~(s)里面的节点; S S S与 P P P相对,是successor,即后继节点,是从 M ~ ( s ) \tilde M(s) M~(s)中出来被指向的节点构成的集合;最后 V V V是这个图中既不在 M M M中,又不在 P P P和 S S S中的节点构成的集合。综上, M M M是已经匹配的节点集合, P P P和 S S S是直接和已经匹配的节点相连的节点集合,V是更外圈的节点集合,下面严格定义一下~
- P ~ 1 ( s ) = { u ∈ V 1 − M ~ 1 ( s ) : ∃ u ′ ∈ M ~ 1 ( s ) : ( u , u ′ ) ∈ E 1 } \tilde P_1(s)=\{u\in V_1-\tilde M_1(s):\exist u^{'}\in \tilde M_1(s):(u,u^{'})\in E_1 \} P~1(s)={u∈V1−M~1(s):∃u′∈M~1(s):(u,u′)∈E1}
- S ~ 1 ( s ) = { u ∈ V 1 − M ~ 1 ( s ) : ∃ u ′ ∈ M ~ 1 ( s ) : ( u ′ , u ) ∈ E 1 } \tilde S_1(s)=\{u\in V_1-\tilde M_1(s):\exist u^{'}\in \tilde M_1(s):(u^{'},u)\in E_1 \} S~1(s)={u∈V1−M~1(s):∃u′∈M~1(s):(u′,u)∈E1}
- V ~ 1 ( s ) = V 1 − M ~ 1 ( s ) − P ~ 1 ( s ) − S ~ 1 ( s ) \tilde V_1(s)=V_1-\tilde M_1(s)-\tilde P_1(s)-\tilde S_1(s) V~1(s)=V1−M~1(s)−P~1(s)−S~1(s)
- P ~ 2 ( s ) = { v ∈ V 2 − M ~ 2 ( s ) : ∃ v ′ ∈ M ~ 2 ( s ) : ( v , v ′ ) ∈ E 2 } \tilde P_2(s)=\{v\in V_2-\tilde M_2(s):\exist v^{'}\in \tilde M_2(s):(v,v^{'})\in E_2 \} P~2(s)={v∈V2−M~2(s):∃v′∈M~2(s):(v,v′)∈E2}
- S ~ 2 ( s ) = { v ∈ V 2 − M ~ 2 ( s ) : ∃ v ′ ∈ M ~ 2 ( s ) : ( v ′ , v ) ∈ E 2 } \tilde S_2(s)=\{v\in V_2-\tilde M_2(s):\exist v^{'}\in \tilde M_2(s):(v^{'},v)\in E_2 \} S~2(s)={v∈V2−M~2(s):∃v′∈M~2(s):(v′,v)∈E2}
- V ~ 2 ( s ) = V 2 − M ~ 2 ( s ) − P ~ 2 ( s ) − S ~ 2 ( s ) \tilde V_2(s)=V_2-\tilde M_2(s)-\tilde P_2(s)-\tilde S_2(s) V~2(s)=V2−M~2(s)−P~2(s)−S~2(s)
几个集合的关系如下图所示~~~
那么当前状态 s s s下,候选节点对集合 P ( s ) P(s) P(s)由哪些节点对构成?任意选一个节点 u ∈ P ~ 1 ( s ) u\in \tilde P_1(s) u∈P~1(s),再任意选一个节点 v ∈ P ~ 2 ( s ) v\in \tilde P_2(s) v∈P~2(s),所有这样的节点构成的节点对 ( u , v ) (u,v) (u,v)都得在 P ( s ) P(s) P(s)里;任意选一个节点 u ∈ S ~ 1 ( s ) u\in \tilde S_1(s) u∈S~1(s),再任意选一个节点 v ∈ S ~ 2 ( s ) v\in \tilde S_2(s) v∈S~2(s),所有这样的节点构成的节点对 ( u , v ) (u,v) (u,v)也得在 P ( s ) P(s) P(s)里;如果能构成上面两种情况的节点对都不存在,任意选一个节点 u ∈ V ~ 1 ( s ) u\in \tilde V_1(s) u∈V~1(s),再任意选一个节点 v ∈ V ~ 2 ( s ) v\in \tilde V_2(s) v∈V~2(s),所有这样的节点构成的节点对 ( u , v ) (u,v) (u,v)组成 P ( s ) P(s) P(s)。
接下来从候选节点对集合 P ( s ) P(s) P(s)中挑选一对节点作为当前的候选节点,VF2算法从中任意拿出一对(其实这里有很多工作可以做,详见VF3),然后进入下一步判断其是否可行。当然,这样可能会出现在整个搜索过程中多次到达同一个状态 s s s的情况,只是每次到达这个状态 s s s时,对应的 M ~ ( s ) \tilde M(s) M~(s)中的节点对进入的顺序不一样,为了在搜索过程中不重复到达同一个状态 s s s,我们在最开始就给小图中的节点一个优先级,这个优先级在VF2中是任意的(这个在VF3中也有很多讲究),比如 u 1 ≺ u 2 ≺ . . . u n u_1\prec u_2\prec...u_n u1≺u2≺...un,如果当前状态下 M ~ ( s ) \tilde M(s) M~(s)中已经有小图节点 u k u_k uk的优先序高于一对节点对中的小图节点 u j u_j uj的优先序,那么 u j u_j uj有关的节点对不会被考虑作为候选节点,这就保证了整棵搜索树中的状态不会重复。
C 可行规则
在匹配过程中,每一步选取的节点对 ( u n , v n ) (u_n,v_n) (un,vn)加入到状态 s s s不一定合适,要么加入后新的状态 s ′ s' s′不是一致状态(consistent state),要么加入后未来几步不可能达到一致状态,因此这一搜索分支就可以被砍掉,不再往下搜索,并且回溯到上一状态 s s s并选取下一节点对。我们要用一系列的可行规则来判断当前选出的候选节点对是否可以加入状态 s s s达到 s ′ s' s′。
我们用可行函数 I s F e a s i b l e ( s c , u n , v n ) IsFeasible(s_c,u_n,v_n) IsFeasible(sc,un,vn)来判断在当前状态 s c s_c sc下,加入节点对 ( u n , v n ) (u_n,v_n) (un,vn)是否可行。判断规则主要分为两类,一类是基于节点和边的标签(label),记作 F s F_s Fs,另一类基于图的拓扑结构,记作 F t F_t Ft。两类规则都得满足,因此有:
I s F e a s i b l e ( s c , u n , v n ) = F s ( s c , u n , v n ) ∧ F t ( s c , u n , v n ) IsFeasible(s_c,u_n,v_n)=F_s(s_c,u_n,v_n)\land F_t(s_c,u_n,v_n) IsFeasible(sc,un,vn)=Fs(sc,un,vn)∧Ft(sc,un,vn)
F s F_s Fs的规则很简单,就是要保证新加入节点对后,对应节点和边的label要全部相同:
- ∀ u ∈ V 1 λ V 1 ( u ) = λ V 2 ( μ ( u ) ) \forall u \in V_1 \quad \lambda_{V_1}(u)=\lambda_{V_2}(\mu(u)) ∀u∈V1λV1(u)=λV2(μ(u))
- ∀ ( u , u ′ ) ∈ E 1 λ e 1 ( u , u ′ ) = λ e 2 ( μ ( u ) , μ ( u ′ ) ) \forall (u,u^{'}) \in E_1 \quad \lambda_{e_1}(u,u^{'})=\lambda_{e_2}(\mu(u),\mu(u^{'})) ∀(u,u′)∈E1λe1(u,u′)=λe2(μ(u),μ(u′))
而 F t F_t Ft的规则就复杂一些,当然这也是本算法剪枝的精髓所在~这部分规则又可以分为三个小部分,第一:将新节点对加入状态 s s s后,检查新的状态 s ′ s' s′还是一致状态,记作 F c F_c Fc;第二,考虑1-lookahead,判断未来一步是否可能构成一致状态 s ′ ′ s'' s′′记作 F l a 1 F_{la1} Fla1;第三,考虑2-lookahead,判断未来两步是否可能构成一致状态 s ′ ′ ′ s''' s′′′,记作 F l a 2 F_{la2} Fla2。
F t ( s c , u n , v n ) = F c ( s c , u n , v n ) ∧ F l a 1 ( s c , u n , v n ) ∧ F l a 2 ( s c , u n , v n ) F_t(s_c,u_n,v_n)=F_c(s_c,u_n,v_n)\land F_{la1}(s_c,u_n,v_n)\land F_{la2}(s_c,u_n,v_n) Ft(sc,un,vn)=Fc(sc,un,vn)∧Fla1(sc,un,vn)∧Fla2(sc,un,vn)
下面逐个展开~
第一类规则 F c F_c Fc:
当 s c s_c sc已经是一个一致状态,判断要新加入的候选节点对 ( u n , v n ) (u_n,v_n) (un,vn)是否可行,需要满足 s c ∪ ( u n , v n ) s_c\cup (u_n,v_n) sc∪(un,vn)依然是一致状态。
F c ( S c , u n , v n ) = ∀ u ′ ∈ S 1 ( u n ) ∩ M ~ 1 ( s c ) ∃ v ′ = μ ~ ( s c , u ′ ) ∈ S 2 ( v n ) ∧ ∀ u ′ ∈ P 1 ( u n ) ∩ M ~ 1 ( s c ) ∃ v ′ = μ ~ ( s c , u ′ ) ∈ P 2 ( v n ) ∧ ∀ v ′ ∈ S 2 ( v n ) ∩ M ~ 2 ( s c ) ∃ u ′ = μ ~ − 1 ( s c , v ′ ) ∈ S 1 ( u n ) ∧ ∀ v ′ ∈ P 2 ( v n ) ∩ M ~ 2 ( s c ) ∃ u ′ = μ ~ − 1 ( s c , v ′ ) ∈ P 1 ( u n ) F_c(S_c,u_n,v_n)= \\ \forall u'\in S_1(u_n)\cap \tilde M_1(s_c)\ \ \exist v'=\tilde \mu(s_c,u')\in S_2(v_n) \\ \land \forall u'\in P_1(u_n)\cap \tilde M_1(s_c)\ \ \exist v'=\tilde \mu(s_c,u')\in P_2(v_n) \\ \land \forall v'\in S_2(v_n)\cap \tilde M_2(s_c)\ \ \exist u'=\tilde \mu ^{-1}(s_c,v')\in S_1(u_n) \\ \land \forall v'\in P_2(v_n)\cap \tilde M_2(s_c)\ \ \exist u'=\tilde \mu ^{-1}(s_c,v')\in P_1(u_n) Fc(Sc,un,vn)=∀u′∈S1(un)∩M~1(sc) ∃v′=μ~(sc,u′)∈S2(vn)∧∀u′∈P1(un)∩M~1(sc) ∃v′=μ~(sc,u′)∈P2(vn)∧∀v′∈S2(vn)∩M~2(sc) ∃u′=μ~−1(sc,v′)∈S1(un)∧∀v′∈P2(vn)∩M~2(sc) ∃u′=μ~−1(sc,v′)∈P1(un)
人话解释一下:
S 1 ( u n ) S_1(u_n) S1(un)是 u n u_n un节点的所有后继节点构成的集合; P 1 ( u n ) P_1(u_n) P1(un)是 u n u_n un节点的所有前驱节点构成的集合;
S 2 ( v n ) S_2(v_n) S2(vn)是 v n v_n vn节点的所有后继节点构成的集合; P 2 ( v n ) P_2(v_n) P2(vn)是 v n v_n vn节点的所有前驱节点构成的集合。
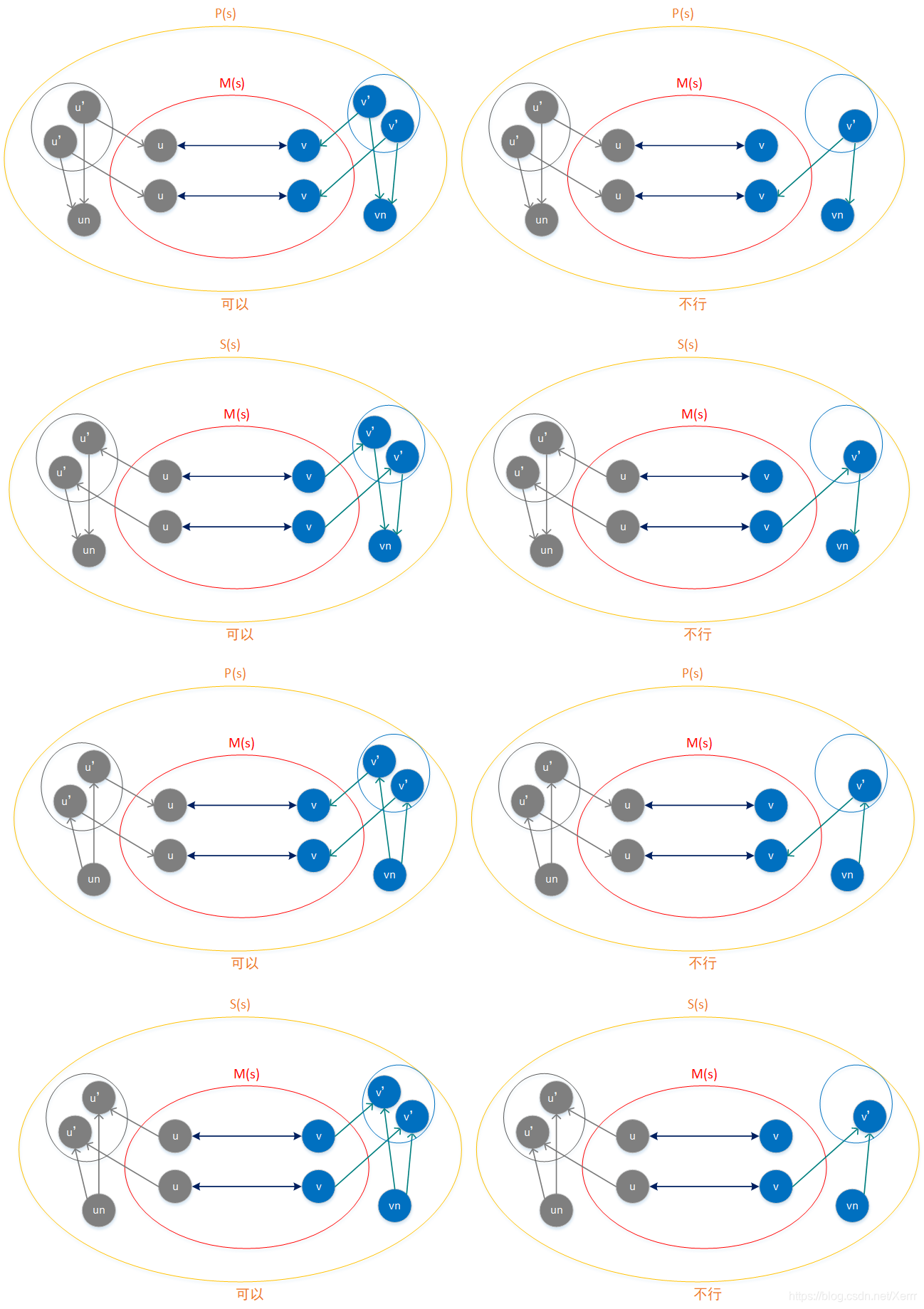
4条规则就说了一件事:新的节点 u n u_n un与已经匹配上的 M ~ 1 ( s c ) \tilde M_1(s_c) M~1(sc)中节点的关系 和 新的节点 v n v_n vn与已经匹配上的 M ~ 2 ( s c ) \tilde M_2(s_c) M~2(sc)中节点的关系 要一模一样!不能左边有右边没有或右边有左边没有,也不能乱了顺序和边的方向。
补充:有的问题需求是,小图中有的边大图中必须有,而大图中有的边小图可以没有,也就是小于等于的关系,那么就把后两条规则删除,也就是最右边的两个图的情况可以被容许。
第二类规则 F l a 1 F_{la1} Fla1:
F l a 1 ( s c , u n , v n ) = ∣ P 1 ( u n ) ∩ P ~ 1 ( s c ) ∣ ≤ ∣ P 2 ( v n ) ∩ P ~ 2 ( s c ) ∣ ∧ ∣ P 1 ( u n ) ∩ S ~ 1 ( s c ) ∣ ≤ ∣ P 2 ( v n ) ∩ S ~ 2 ( s c ) ∣ ∧ ∣ S 1 ( u n ) ∩ P ~ 1 ( s c ) ∣ ≤ ∣ S 2 ( v n ) ∩ P ~ 2 ( s c ) ∣ ∧ ∣ S 1 ( u n ) ∩ S ~ 1 ( s c ) ∣ ≤ ∣ S 2 ( v n ) ∩ S ~ 2 ( s c ) ∣ F_{la1}(s_c,u_n,v_n)=\\ |P_1(u_n)\cap \tilde P_1(s_c)|\le |P_2(v_n)\cap \tilde P_2(s_c)| \\ \land |P_1(u_n)\cap \tilde S_1(s_c)|\le |P_2(v_n)\cap \tilde S_2(s_c)| \\ \land |S_1(u_n)\cap \tilde P_1(s_c)|\le |S_2(v_n)\cap \tilde P_2(s_c)| \\ \land |S_1(u_n)\cap \tilde S_1(s_c)|\le |S_2(v_n)\cap \tilde S_2(s_c)| Fla1(sc,un,vn)=∣P1(un)∩P~1(sc)∣≤∣P2(vn)∩P~2(sc)∣∧∣P1(un)∩S~1(sc)∣≤∣P2(vn)∩S~2(sc)∣∧∣S1(un)∩P~1(sc)∣≤∣S2(vn)∩P~2(sc)∣∧∣S1(un)∩S~1(sc)∣≤∣S2(vn)∩S~2(sc)∣
这一类约束主要考虑与当前状态 s c s_c sc中的节点直接相连的节点( P , S P,S P,S集合)与新的节点对 ( u n , v n ) (u_n,v_n) (un,vn)间的关系。现在考虑的是3部分节点,1是已经在 M ( s c ) M(s_c) M(sc)中的节点,即已经匹配了的;2是新的候选节点;3是 P , S P,S P,S集合中的节点。3的节点中,与1和2的关系可以分成四类,分别对应上述4条规则,每一类关系的节点数量都要满足:小图节点数量不大于大图节点数量,若小图某一类的节点数大于大图了,说明未来不可能形成一致状态,因为未来必然会有小图中边,在大图中找不到。
第三类规则 F l a 2 F_{la2} Fla2:
F l a 2 ( s c , u n , v n ) = ∣ P 1 ( u n ) ∩ V ~ 1 ( s c ) ∣ ≤ ∣ P 2 ( v n ) ∩ V ~ 2 ( s c ) ∣ ∧ ∣ S 1 ( u n ) ∩ V ~ 1 ( s c ) ∣ ≤ ∣ S 2 ( v n ) ∩ V ~ 2 ( s c ) ∣ F_{la2}(s_c,u_n,v_n)= \\ |P_1(u_n)\cap \tilde V_1(s_c)|\le |P_2(v_n)\cap \tilde V_2(s_c)| \\ \land |S_1(u_n)\cap \tilde V_1(s_c)|\le |S_2(v_n)\cap \tilde V_2(s_c)| Fla2(sc,un,vn)=∣P1(un)∩V~1(sc)∣≤∣P2(vn)∩V~2(sc)∣∧∣S1(un)∩V~1(sc)∣≤∣S2(vn)∩V~2(sc)∣
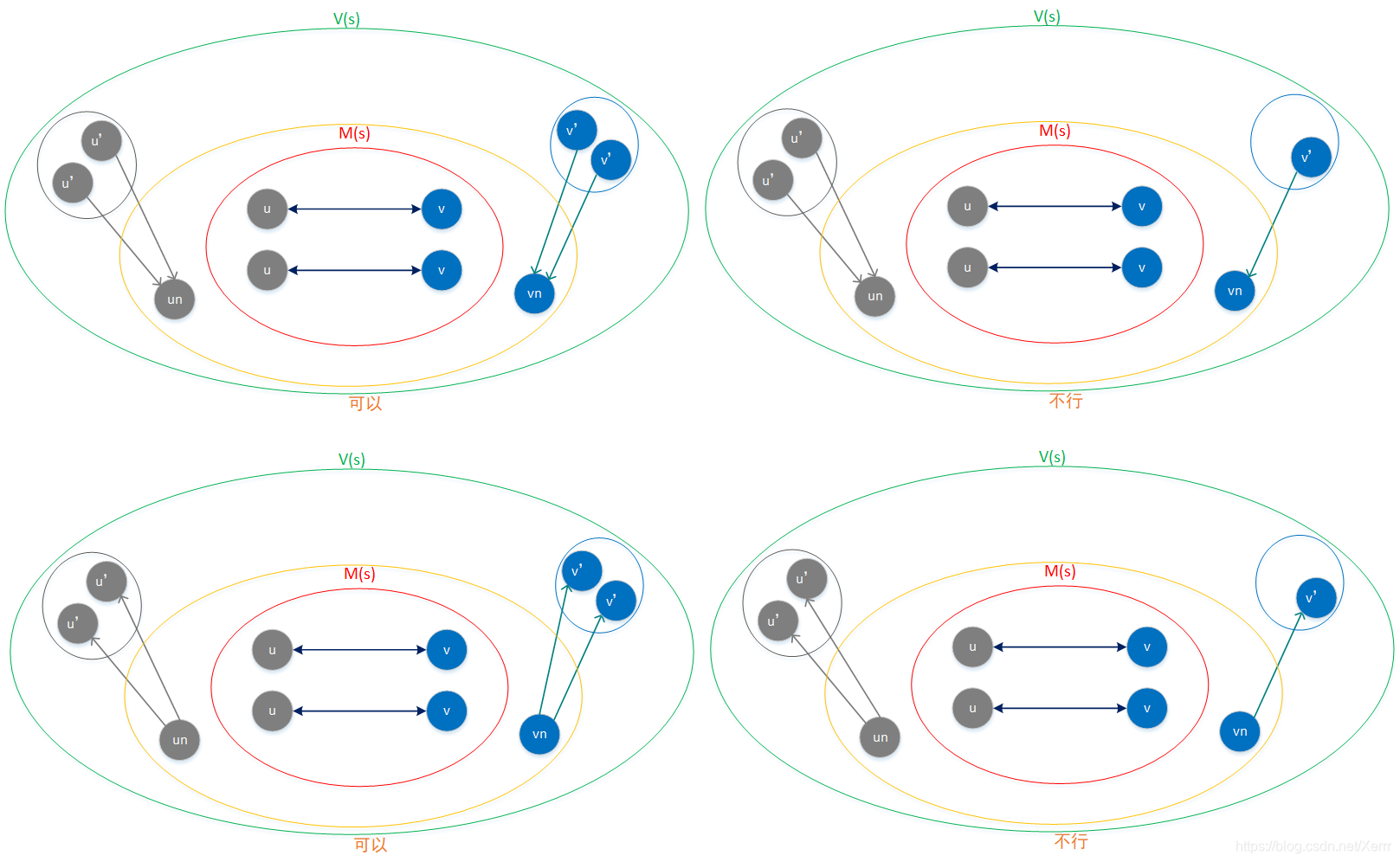
这一类约束主要考虑与当前状态 s c s_c sc中的节点不直接相连的节点( V V V集合)与新的节点对 ( u n , v n ) (u_n,v_n) (un,vn)间的关系。现在考虑的是3部分节点,1是已经在 M ( s c ) M(s_c) M(sc)中的节点,即已经匹配了的;2是新的候选节点;3是 V V V集合中的节点。3的节点中,与1和2的关系可以分成2类,分别对应上述2条规则,每一类关系的节点数量都要满足:小图节点数量不大于大图节点数量,若小图某一类的节点数大于大图了,说明未来不可能形成一致状态,因为未来必然会有小图中边,在大图中找不到。
上述三类规则其实是把新节点对 ( u n , v n ) (u_n,v_n) (un,vn)的度分成三部分,第一部分是与 M ( s ) M(s) M(s)中节点的连接;第二部分是与 P ( s ) 、 V ( s ) P(s)、V(s) P(s)、V(s)中节点的连接,即1-lookahead;第三部分是与 V ( s ) V(s) V(s)中节点的连接,即2-lookahead。这三类连接又可以分为入度和出度,与其连接的节点又可以按分组分开,其中第一部分 M ( s ) M(s) M(s)中已经匹配上的节点分组一定相同,因此可以不考虑分组。这样分类后,每一类度的数量都要满足,小图不大于大图,否则将不可能同构,其中第一类比较特殊,必须完全相同才能同构,当然也有只需要小于等于的需求,这类需求严格意义上已经不是子图同构了。
3 总结
VF算法的搜索树其实跟Ullmann算法是一样的,只不过Ullmann用矩阵表示每一个状态 s s s,VF2算法最核心的就是可行规则,提前筛除了很多不必要的分支,而后面的VF3算法在VF2的基础上加入了候选节点选择时的顺序,可以在更早的时候剪掉更多大分支,并且在可行规则中给节点分了类,进一步加大剪枝力度~