C++常用数据结构
链表
链表(单链表)的基本操作及C语言实现
链表中存放的不是基本数据类型,需要用结构体实现自定义:
typedef struct Link
{
char elem;//代表数据域
struct Link * next;//代表指针域,指向直接后继元素
}link;
next的值实际上就是下一个节点的地址,当前节点为末节点时,next的值设为空指针。像上面这种只包含一个指针域、由n个节点链接形成的链表,就称为线型链表或者单向链表,链表只能顺序访问,不能随机访问,链表这种存储方式最大缺点就是容易出现断链。
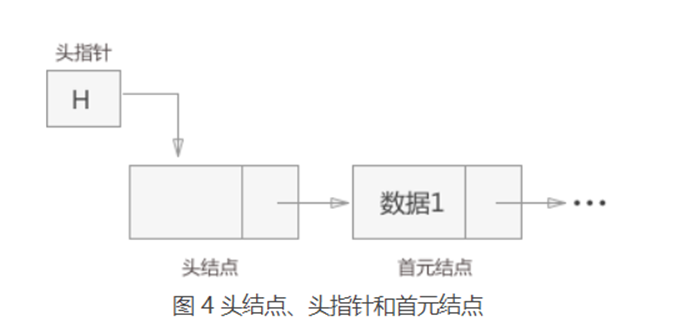
头结点和头指针的区别:
头指针是一个指针,头指针指向链表的头结点或者首元结点;头结点是一个实际存在的结点,它包含有数据域和指针域。两者在程序中的直接体现就是:头指针只声明而没有分配存储空间,头结点进行了声明并分配了一个结点的实际物理内存。单链表中可以没有头结点,但是不能没有头指针!
单向链表+头指针+尾指针:
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
ListNode *head = nullptr, *tail = nullptr;
//从尾部插入结点
head = tail = new ListNode(num1);
tail->next = new ListNode(num2);
tail = tail->next;
注意:nullptr在C++11中就是代表空指针,不能被转换成数字。在编译器进行解释程序时,NULL会被直接解释成0。
链表的题通常需要注意几点:
- 舍得用变量,千万别想着节省变量,否则容易被逻辑绕晕
- head 有可能需要改动时,先增加一个 假head,返回的时候直接取 假head.next,这样就不需要为修改 head 增加一大堆逻辑了。
- while(p->next&&p->next->next)
while(p->next&&p->next->val==x)
p->next必须要写在前面
ListNode *k=new ListNode(0,head);//不要省建立头结点的功夫
此外还需要注意,能用f作为判定条件,就尽量不要以f->next作为判定条件,若f直接为空指针,会直接炸掉。这里涉及到短路或、短路与的概念。
//尽量不要以f->next作为判定条件,若f直接为空指针,会直接炸掉
下面这个方法不好
while(f->next&&i<index-1)
{
f=f->next;
i++;
}
//改成下面的样子比较好
NodeList* f =head;
int i=0;
while(f&&i<index-1)
{
f=f->next;
i++;
}
if(!f)//超出链表范围则退出
{
return;
}
if(f->next)
{
NodeList* m=f->next;
f->next=m->next;
delete m;//delete与new匹配
}
单向链表常用的初始化:
//单向链表常用的初始化
class MyLinkedList {
private:
struct NodeList
{
int val;
NodeList* next;
NodeList():val(0),next(nullptr){}//{}
NodeList(int n):val(n),next(nullptr){}
};//;
NodeList * head;
public:
MyLinkedList():head(nullptr) {}//默认构造函数,调用时不用加()
Main函数调用MyLinkedList list;//不需要(),加括号会被误认为调用函数
C++双向链表模板:
//C++双向链表模板
class MyList
{
private:
struct ListNode
{
int val;
ListNode *next,*prev;
ListNode(int x):val(x),next(nullptr),prev(nullptr){}
};
private:
//头节点尾节点都为空,表示为空链表
ListNode *head,*tail;
int size=0;
public:
MyList():size(0),head(nullptr),tail(nullptr){}
反转链表:
从前往后挨着元素反转,并记录反转头prev,剩下未反转部分的头curr,以及下一个元素next。直到剩下未反转头curr为空。Prev初始值也为空,curr初始值为head。
ListNode* reverseList(ListNode* head)
{
ListNode* pre = nullptr;
ListNode* cur = head;
ListNode* nex ;
while(cur)
{
nex = cur->next;//提前该语句
cur->next=pre;
pre=cur;
cur=nex;
// nex = cur->next;//当cur为空指针时该语句会报错,运行超时,需要将该语句提前
}
return pre;
}
易错点是while判定条件里next需要提前写,将实际遍历的结点作为判定条件,否则容易runtime error。
内存的申请与释放
free和delete区别_prerfect_cat的博客
free和mall匹配:释放malloc出来动态内存;
delete和new匹配:释放new出来的动态内存空间。
在类和对象的时候会有很大区别。在使用malloc和free来处理动态内存的时候,仅仅是释放了这个对象所占的内存,而不会调用这个对象的析构函数;使用new和delete就可以既释放对象的内存的同时,调用这个对象的析构函数。
delete释放对象数组时:千万不能丢失”[]”
如果用new 创建对象数组,那么只能使用对象的无参数构造函数。例如
Obj *objects = new Obj[100]; // 创建100 个动态对象
在用delete 释放对象数组时,留意不要丢了符号‘[ ]’。例如
delete []objects; // 正确的用法
delete objects; // 错误的用法
后者相当于delete objects[0],漏掉了另外99 个对象。
new出来的是一段空间的首地址。所以一般需要用指针来存放这段地址。
//可以在new后面直接赋值
int *p = new int(3);
//也可以单独赋值
//*p = 3;
//如果不想使用指针,可以定义一个变量,在new之前用“*”表示new出来的内容
int q = *new int;
//当new一个数组时,同样用一个指针接住数组的首地址
int *q = new int[3];
//这里是用一个结构体指针接住结构体数组的首地址
//对于结构体指针,个人认为目前这种赋值方法比较方便
struct student
{
string name;
int score;
};
student *stlist = new student[3]{{"abc", 90}, {"bac", 78}, {"ccd", 93}};
滑动窗口
什么是滑动窗口?
其实就是一个队列,比如下面例题中的字符串 abcabcbb,进入这个队列(窗口)为 abc 满足题目要求,当再进入 a,队列变成了 abca,这时候不满足要求。所以,我们要移动这个队列!
如何移动?
我们只要把队列的左边的元素移出就行了,直到满足题目要求!
一直维持这样的队列,找出队列出现最长的长度时候,求出解!
时间复杂度:O(n)
3. 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例:
输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”,所以其长度为 3。
请注意,你的答案必须是 子串 的长度,“pwke” 是一个子序列,不是子串。
【分析】
用滑动窗口,固定最左边 l,每次都从最右边 r 开始扩张,出现重复元素时,删除哈希集合中从 l 到重复元素下标之间的元素,将 l 进行更新,并继续向右扩张 r 。
关键点:如果依次递增地枚举子串的起始位置,那么子串的结束位置也是递增的!因为当前结束位置前面都是无重复子串了,删掉最左边起始位置后,剩下的这一截更是无重复子串,所以每次移动右窗口指针时候只需要从上次结束位置开始就行。
用哈希集合判断重复。
int lengthOfLongestSubstring(string s) {
if(s.empty()) return 0;
int n = s.size();
unordered_set<char> st;
int l = 0, maxlen = 0;
for(int r = 0; r < n; ++r){
//删除哈希集合中从 l 到重复元素下标之间的元素,将 l 进行更新
while(st.find(s[r]) != st.end()){
st.erase(s[l]);
++l;
}
//每次右移r时,就更新一下最长长度,
//以免出现整个字符串都无重复,遍历到头一直没更新长度的情况
maxlen = max(r - l + 1, maxlen);
st.insert(s[r]);
}
return maxlen;
}
也可以用哈希表实现,用哈希表记录每个元素出现的下标,可以精确知道删除重复元素时的循环次数。
int lengthOfLongestSubstring(string s) {
if(s.empty()) return 0;
int n = s.size();
unordered_map<char, int> mp;
//每次固定l, 右移r,出现重复元素时再更新l
int l = 0, maxlen = 0;
for(int r = 0; r < n; ++r){
//若发现重复字符,则通过哈希表找到第一个重复下标
//删除从l到重复下标之间的哈希表元素,并将l重置为重复下标的下一个位置
if(mp.find(s[r]) != mp.end()){
int newl = mp[s[r]] + 1;
for(int i = l; i < newl; i++){
mp.erase(s[i]);
}
l = newl;
}
//每次右移r时,就更新一下最长长度,
//以免出现整个字符串都无重复,遍历到头一直没更新长度的情况
maxlen = max(r - l + 1, maxlen);
mp[s[r]] = r;;
}
return maxlen;
}
76. 最小覆盖子串
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = “ADOBECODEBANC”, t = “ABC”
输出:“BANC”
【分析】滑动窗口
我们可以用滑动窗口的思想解决这个问题。在滑动窗口类型的问题中都会有两个指针,一个用于「延伸」现有窗口的 r 指针,和一个用于「收缩」窗口的 l 指针。在任意时刻,只有一个指针运动,而另一个保持静止。我们在 s 上滑动窗口,通过移动 r 指针不断扩张窗口。当窗口包含 t 全部所需的字符后,如果能收缩,我们就收缩窗口直到得到最小窗口。
如何判断当前的窗口包含所有 t 所需的字符呢?我们可以用一个哈希表表示 t 中所有的字符以及它们的个数,用一个哈希表动态维护窗口中所有的字符以及它们的个数,如果这个动态表中包含 t 的哈希表中的所有字符,并且对应的个数都不小于 t 的哈希表中各个字符的个数,那么当前的窗口是「可行」的。
注意:这里 t 中可能出现重复的字符,所以我们要记录字符的个数。
举个例子:
如果
s
=
X
X
⋯
X
A
B
C
X
X
X
X
s = {\rm XX \cdots XABCXXXX}
s=XX⋯XABCXXXX,
t
=
A
B
C
t = {\rm ABC}
t=ABC,那么显然
[
X
X
⋯
X
A
B
C
]
{\rm [XX \cdots XABC]}
[XX⋯XABC] 是第一个得到的「可行」区间,得到这个可行区间后,我们按照「收缩」窗口的原则更新左边界,得到最小区间。
unordered_map<char, int> ori, cnt;
bool check(){
for(const auto& f:ori){
if(cnt[f.first] < f.second){
return false;
}
}
return true;
}
string minWindow(string s, string t) {
for(const char& c:t){
ori[c]++;
}
int l = 0, r = 0, ansl = -1;
int len = INT_MAX, n = s.size();
while(r < n){
if(ori.find(s[r]) != ori.end()){
cnt[s[r]]++;
}
++r;
while(check() && l <= r){
if(r - l < len){
len = r - l;
ansl = l;
}
if(ori.find(s[l]) != ori.end()){
cnt[s[l]]--;
}
++l;
}
}
return ansl == -1 ? string() : s.substr(ansl, len);
}
其他滑动窗口例题:
滑动窗口讲解
例题讲解:
438. 找到字符串中所有字母异位词
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
示例 1:
输入: s = “cbaebabacd”, p = “abc”
输出: [0,6]
解释: 起始索引等于 0 的子串是 “cba”, 它是"abc" 的异位词。 起始索引等于 6 的子串是 “bac”, 它是 “abc” 的异位词。
【分析】
在字符串 s 中构造一个长度为与字符串 p 的长度相同的滑动窗口,并在滑动中维护窗口中每种字母的数量;当窗口中每种字母的数量与字符串 p 中每种字母的数量相同时,则说明当前窗口为字符串 p 的异位词。
在算法的实现中,可以使用数组来存储字符串 pp 和滑动窗口中每种字母的数量。
【细节】
当字符串 s 的长度小于字符串 p 的长度时,字符串 s 中一定不存在字符串 p 的异位词。但是因为字符串 s 中无法构造长度与字符串 p 的长度相同的窗口,所以这种情况需要单独处理。
此外,比较两个数组是否相等时,可以直接用 “数组1 == 数组2” 来判断。
vector<int> findAnagrams(string s, string p) {
int m = p.size(), n = s.size();
if(n < m) return {};
vector<int> ans;
vector<int> scount(26);
vector<int> pcount(26);
for(int i = 0; i < m; ++i){
++scount[s[i] - 'a'];
++pcount[p[i] - 'a'];
}
for(int l = 0; l + m <= n; ++l){
if(l != 0){
++scount[s[l + m -1] - 'a'];
--scount[s[l - 1] - 'a'];
}
//判断两个数组是否相等,可以直接用 ==
if(scount == pcount){
ans.emplace_back(l);
}
}
return ans;
}
下面第30题的过渡版写法:
用了一个哈希表来进出字符,初始时先存p的哈希值,再减去s中第一个窗口的哈希值,之后对s进行窗口滑动,以及哈希表字符进出,当字符键值为0时删除该字符,当哈希表为空时表示匹配成功,可以存入输出数组。
vector<int> findAnagrams(string s, string p) {
vector<int> ans;
unordered_map<char, int> mp;
int m = p.size(), n = s.size();
//用字符串 p 来初始化哈希表
for(char &ch : p){
++mp[ch];
}
//字符串 s 的首个窗口
for(int i = 0; i < m && i < n; ++i){
if(--mp[s[i]] == 0){
mp.erase(s[i]);
}
}
//对字符串 s 进行滑动窗口
for(int l = 0; l + m <= n; ++l){
if(l != 0){
//注意这里的++ 与 --特别容易搞混
if(--mp[s[l + m - 1]] == 0) mp.erase(s[l + m - 1]);
if(++mp[s[l - 1]] == 0) mp.erase(s[l - 1]);
}
if(mp.empty()){
ans.emplace_back(l);
}
}
return ans;
}
30. 串联所有单词的子串
给定一个字符串 s 和一些 长度相同 的单词 words 。找出 s 中恰好可以由 words 中所有单词串联形成的子串的起始位置。
注意子串要与 words 中的单词完全匹配,中间不能有其他字符 ,但不需要考虑 words 中单词串联的顺序。
示例 1:
输入:s = “barfoothefoobarman”, words = [“foo”,“bar”]
输出:[0,9]
解释:从索引 0 和 9 开始的子串分别是 “barfoo” 和 “foobar” 。 输出的顺序不重要, [9,0] 也是有效答案。
【分析】
记
words
\textit{words}
words 的长度为
m
m
m,
words
\textit{words}
words 中每个单词的长度为
n
n
n,
s
s
s 的长度为
ls
\textit{ls}
ls。首先需要将
s
s
s 划分为单词组,每个单词的大小均为
n
n
n (首尾除外)。这样的划分方法有
n
n
n 种,即先删去前
i
i
i (
i
=
0
∼
n
−
1
i = 0 \sim n-1
i=0∼n−1)个字母后,将剩下的字母进行划分,如果末尾有不到
n
n
n 个字母也删去。对这
n
n
n 种划分得到的单词数组分别使用滑动窗口对
words
\textit{words}
words 进行类似于「字母异位词」的搜寻。
划分成单词组后,一个窗口包含 s s s 中前 m m m 个单词,用一个哈希表 differ \textit{differ} differ 表示窗口中单词频次和 words \textit{words} words 中单词频次之差。初始化 differ \textit{differ} differ 时,出现在窗口中的单词,每出现一次,相应的值增加 1,出现在 words \textit{words} words 中的单词,每出现一次,相应的值减少 1。然后将窗口右移,右侧会加入一个单词,左侧会移出一个单词,并对 differ \textit{differ} differ 做相应的更新。窗口移动时,若出现 differ \textit{differ} differ 中值不为 0 的键的数量为 0,则表示这个窗口中的单词频次和 words \textit{words} words 中单词频次相同,窗口的左端点是一个待求的起始位置。划分的方法有 n n n 种,做 n n n 次滑动窗口后,即可找到所有的起始位置。
vector<int> findSubstring(string s, vector<string>& words) {
vector<int> ans;
int m = words.size();
int n = words[0].size();
int ls = s.size();
//注意添加&& i + m * n 长度限制
for(int i = 0; i < n && i + m * n <= ls; ++i){
unordered_map<string, int> mp;
//现将 s 中前 m 个单词作为初始化窗口
for(int j = 0; j < m; ++j){
string str = s.substr(i + j * n, n);//注意添加起始位置,i +
mp[str]++;
}
for(string &str : words){
if(--mp[str] == 0){
mp.erase(str);
}
}
//向后边滑动窗口
for(int l = i; l + m * n <= ls; l += n){
if(l != i){
string str = s.substr(l - n, n);
if(--mp[str] == 0){
mp.erase(str);
}
str = s.substr(l + (m - 1) * n, n);
if(++mp[str] == 0){ // == 0
mp.erase(str);
}
}
if(mp.empty()){
ans.emplace_back(l);
}
}
}
return ans;
}
前缀和/积与后缀和/积
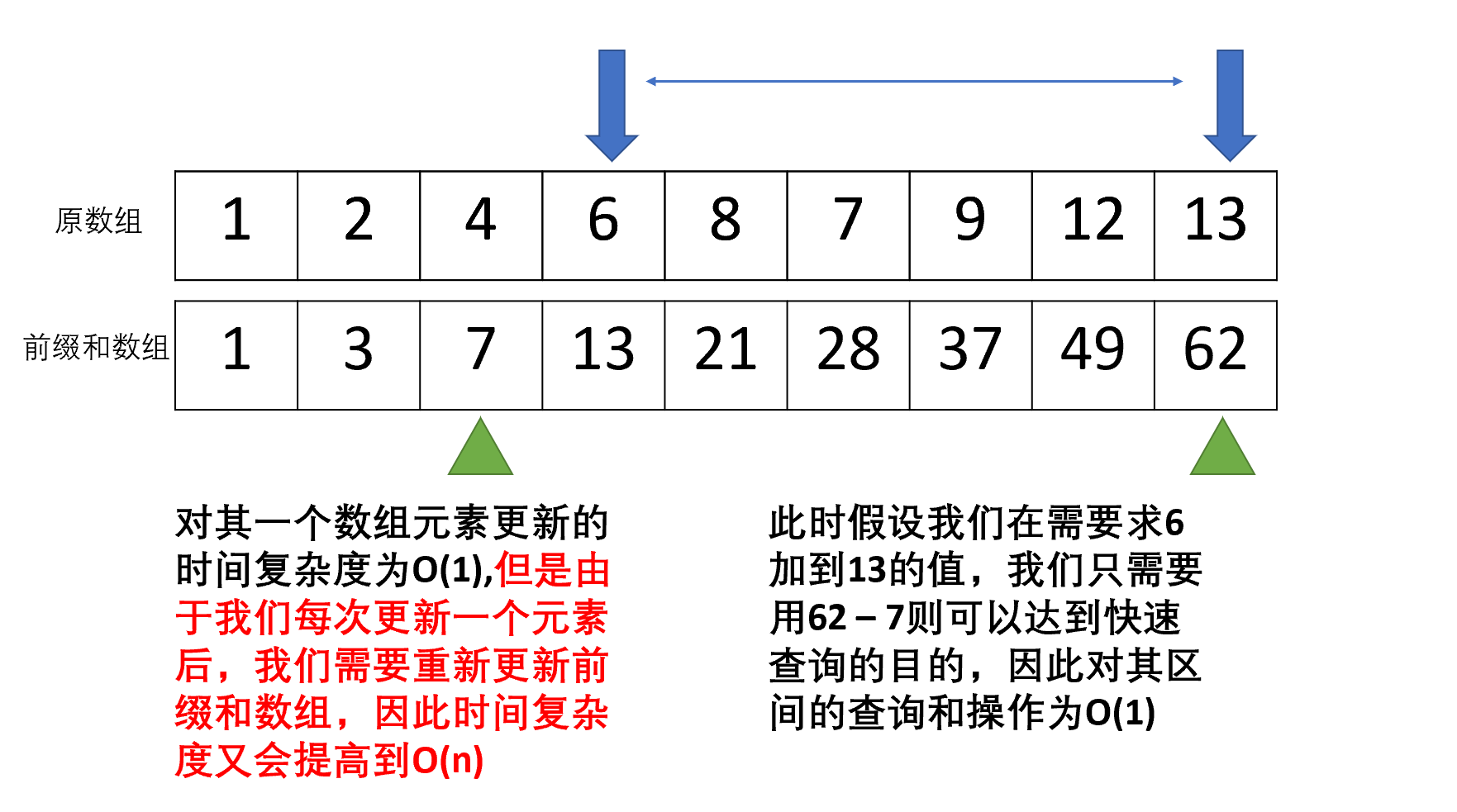
前缀和/积与后缀和/积不是什么数据结构,而是一种常用的技巧。常用于查询连续区间和是否为k,以及区间值运算等问题。
前缀和经常和哈希表结合,这样可以将查询的操作提升到O(1), 但是使用前缀和会有一个问题,当我们的更新次数过多时,尤其是需要更新的元素比较靠前时,每一次更新的代价都会为O(n),从而没有达到优化的效果。前缀和适用于元素不变动的数组!
前缀和非常经典的一道好题:
560. 和为 K 的子数组
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。
示例 1:
输入:nums = [1,1,1], k = 2
输出:2
示例 2:
输入:nums = [1,2,3], k = 3
输出:2
【分析】前缀和 + 哈希表优化
定义
pre
[
i
]
\textit{pre}[i]
pre[i] 为
[
0..
i
]
[0..i]
[0..i] 里所有数的和,我们需要统计符合条件的下标
j
j
j 的个数,其中
0
≤
j
≤
i
0\leq j\leq i
0≤j≤i 且
[
j
.
.
i
]
[j..i]
[j..i] 这个子数组的和恰好为
k
k
k 。
考虑以
i
i
i 结尾的和为
k
k
k 的连续子数组个数时只要统计有多少个前缀和为
pre
[
i
]
−
k
\textit{pre}[i]-k
pre[i]−k 的
pre
[
j
]
\textit{pre}[j]
pre[j] 即可。我们建立哈希表
mp
\textit{mp}
mp,以和为键,出现次数为对应的值,记录
pre
[
i
]
\textit{pre}[i]
pre[i] 出现的次数,从左往右边更新
mp
\textit{mp}
mp 边计算答案,那么以
i
i
i 结尾的答案
mp
[
pre
[
i
]
−
k
]
\textit{mp}[\textit{pre}[i]-k]
mp[pre[i]−k] 即可在
O
(
1
)
O(1)
O(1) 时间内得到。最后的答案即为所有下标结尾的和为
k
k
k 的子数组个数之和。
需要注意的是,从左往右边更新边计算的时候已经保证了 mp [ pre [ i ] − k ] \textit{mp}[\textit{pre}[i]-k] mp[pre[i]−k] 里记录的 pre [ j ] \textit{pre}[j] pre[j] 的下标范围是 0 ≤ j ≤ i 0\leq j\leq i 0≤j≤i 。同时,由于 pre [ i ] \textit{pre}[i] pre[i] 的计算只与前一项的答案有关,因此我们可以不用建立 pre \textit{pre} pre 数组,直接用 pre \textit{pre} pre 变量来记录 p r e [ i − 1 ] pre[i-1] pre[i−1] 的答案即可。
int subarraySum(vector<int>& nums, int k) {
unordered_map<int, int> mp;
mp[0] = 1;
int pre = 0, ans = 0;
for(int &a:nums){
pre += a;
ans += mp[pre - k]; //if (mp.find(pre - k) != mp.end())
mp[pre]++;
}
return ans;
}
前缀积与后缀积的经典例题:
剑指 Offer 66. 构建乘积数组
给定一个数组 A[0,1,…,n-1],请构建一个数组 B[0,1,…,n-1],其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。
示例:
输入: [1,2,3,4,5]
输出: [120,60,40,30,24]
【分析】
我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案,而是利用索引左侧所有数字的乘积和右侧所有数字的乘积(即前缀与后缀)相乘得到答案。
对于给定索引 i i i,我们将使用它左边所有数字的乘积乘以右边所有数字的乘积。由于输出数组不算在空间复杂度内,所以可以先利用输出数组作为前缀和数组,然后再在输出数组的基础上×后缀和(用一个变量表示即可),从而大大节省空间。
算法
1)初始化 ans 数组,对于给定索引 i,
a
n
s
[
i
]
ans[i]
ans[i] 代表的是 i 左侧所有数字的乘积。
2)不用构造后缀和数组,而是用一个变量
r
r
r 表示索引 i 右侧数字的乘积。通过遍历来不断更新右侧元素的乘积 r 。更新数组
a
n
s
[
i
]
=
a
n
s
[
i
]
∗
r
ans[i]=ans[i]*r
ans[i]=ans[i]∗r ,然后
r
r
r 更新为
r
=
r
∗
a
[
i
]
r=r*a[i]
r=r∗a[i]。
vector<int> constructArr(vector<int>& a) {
int n = a.size();
vector<int> ans(n);
if(a.empty()) return ans;
// ans[i] 表示索引 i 左侧所有元素的乘积
// 因为索引为 '0' 的元素左侧没有元素, 所以 ans[0] = 1
ans[0] = 1;
for(int i = 1; i < n; ++i){
ans[i] = ans[i - 1] * a[i - 1];
}
// r 为右侧所有元素的乘积
// 刚开始右边没有元素,所以 r = 1
int r = 1;
for(int i = n - 1; i >= 0; --i){
// 对于索引 i,左边的乘积为 ans[i],右边的乘积为 r
ans[i] *= r;
// r 需要包含右边所有的乘积,所以计算下一个结果时需要将当前值乘到 r 上
r *= a[i];
}
return ans;
}
差分数组
差分数组又叫插旗法,利用差分前缀和来求解公交车上下车和插旗问题等区间更新、区间重叠(活动安排)问题。
差分数组是把原数组中后一个元素减前一个元素的差构成一个新的数组,作为辅助数组使用。通常用map 数据结构实现,如下图所示:

差分数组有什么用?
diff[0] = nums[0];
diff[1] = nums[1] - nums[0];
diff[2] = nums[2] - nums[1];
…
nums[0] = diff[0];
nums[1] = diff[1] + nums[0] = diff[0] + diff[1];
nums[2] = nums[1] + diff[2] = diff[0] + diff[1] + diff[2];
…
nums[n] = diff[0] + diff[1] +diff[2] +…+ diff[n]
由上可知:根据差分数组各项的前缀和,即可还原出原数组的各值,差分数组常用于对区间内元素值的统一修改。 假设我们频繁得对原数组进行范围更新,则只需要更新差分数组端点值即可。
应用举例1:
假如把 nums 数组中 [0,3] 范围到元素值都加 2:
常规方法:
for( int i =0;i < 4;++i)
{
nums[i] += 2;
}
差分数组:
map<int, int> diff;
diff[0] += 2;// 0 往后到值全部加 2
diff[4] -= 2;// 4 往后到值全部减 2
应用举例2:
在区间 [10, 15) [12, 18) 内进行插旗,判断插旗区间是否有重叠。
插旗子 计数:
对于每个区间[start,end),在 start 计数diff[start] 加 1,表示从start 开始插旗的数目加 1;从 end 计数diff[end] 减 1,表示从 end 开始插旗的数目减 1。若差分数组前缀和 >1 即表示到当前位置为止的插旗区有重叠。
| 区间原数组nums | 10 | 12 | 15 | 18 |
|---|---|---|---|---|
| 差分数组diff | 1 | 1 | -1 | -1 |
【分析】
建立差分数组diff,nums数组中的每个区间的start对应的差分数组计数 ++, end 对应的差分数组计数 – ,注意每个区间的start 和 end 是分别作为独立key 存储到查分数组中的,对应的value分别为++和–之后的值 ,而不是start 对应 key,end 对应value这样存储。
所有区间的 start 和 end 存储到 map 中后,一起按照key从大到小的顺序排序
//nums = {{10, 15}, {12, 18}}
//建立差分数组diff,每个区间的start对应的差分数组计数 ++, end 对应的差分数组计数 --
//注意每个区间的start 和 end 是分别作为独立key 存储到查分数组中的,对应的value分别为++和--之后的值
//而不是start 对应 key,end 对应value这样存储。
//所有区间的 start 和 end 存储到 map 中后,一起按照key从大到小的顺序排序
map<int, int> diff;
for(auto v:nums){
diff[v[0]] ++;
diff[v[1]] --;
}
//遍历差分数组,用cnt进行插旗计数,大于1则说明区间重叠
int cnt = 0;
for(auto w:diff){
cnt += w.second;
if(cnt > 1){
cout <<"插旗区间出现重叠" <<endl;
break;
}
}
如果 两个Interval 不相交,则 连续两个 插旗计数的 和 必然等于零,一个+1,一个-1
如果 两个 Interval 相交,则 连续两个插旗计数 的和 必然大于0,一个+1,一个+1
732. 我的日程安排表 III
当 k 个日程安排有一些时间上的交叉时(例如 k 个日程安排都在同一时间内),就会产生 k 次预订。
给你一些日程安排 [start, end) ,请你在每个日程安排添加后,返回一个整数 k ,表示所有先前日程安排会产生的最大 k 次预订。
实现一个 MyCalendarThree 类来存放你的日程安排,你可以一直添加新的日程安排。
MyCalendarThree() 初始化对象。
int book(int start, int end) 返回一个整数 k ,表示日历中存在的 k 次预订的最大值。
示例:
输入:
[“MyCalendarThree”, “book”, “book”, “book”, “book”, “book”, “book”]
[[], [10, 20], [50, 60], [10, 40], [5, 15], [5, 10], [25, 55]]
输出:
[null, 1, 1, 2, 3, 3, 3]
解释:
MyCalendarThree myCalendarThree = new MyCalendarThree();
myCalendarThree.book(10, 20); // 返回 1 ,第一个日程安排可以预订并且不存在相交,所以最大 k 次预订是1 次预订。
myCalendarThree.book(50, 60); // 返回 1 ,第二个日程安排可以预订并且不存在相交,所以最大 k 次预订是 1 次预订。
myCalendarThree.book(10, 40); // 返回 2 ,第三个日程安排 [10, 40)与第一个日程安排相交,所以最大 k 次预订是 2 次预订。 myCalendarThree.book(5, 15); // 返回 3,剩下的日程安排的最大 k 次预订是 3 次预订。
myCalendarThree.book(5, 10); // 返回 3
myCalendarThree.book(25, 55); // 返回 3
题目翻译:
有一个数组初始值全部为 0 ,每次调用 book 方法都把 [start,end) 范围内的所有元素加 1,并返回当前数组中的最大值。
【解答】
直接构建差分数组,更改区间值后再用前缀和还原出原数组即可。
利用差分数组的思想,每当我们预定一个新的日程安排[start,end),在 start 计数diff[start] 加 1,表示从start 预定的数目加 1;从 end 计数diff[end] 减 1,表示从 end 开始预定的数目减 1。从起点开始的计数累加值(前缀和)即为当前位置原数组的值(也就是该区间日程的安排次数)
【注意点】
- book传入的区间是左闭右开 所以[5,10) 跟 [10,…) 不会有 overlap 交叉
- map 自带按key值的递增排序.
代码
class MyCalendarThree {
public:
MyCalendarThree() {}
int book(int start, int end) {
diff[start]++;// start 开始的值都加 1
diff[end]--;// end 开始的值都减 1
int res = 0;
int cur = 0;
for( auto & kv : diff )
{
cur += kv.second;//前缀和还原原数组值
res = max(res,cur);
}
return res;
}
private:
map<int,int> diff;//差分数组
};
731. 我的日程安排表 II
实现一个 MyCalendar 类来存放你的日程安排。如果要添加的时间内不会导致三重预订时,则可以存储这个新的日程安排。
MyCalendar 有一个 book(int start, int end)方法。它意味着在 start 到 end 时间内增加一个日程安排,注意,这里的时间是半开区间,即 [start, end), 实数 x 的范围为, start <= x < end。
当三个日程安排有一些时间上的交叉时(例如三个日程安排都在同一时间内),就会产生三重预订。
每次调用 MyCalendar.book方法时,如果可以将日程安排成功添加到日历中而不会导致三重预订,返回 true。否则,返回 false 并且不要将该日程安排添加到日历中。
请按照以下步骤调用MyCalendar 类: MyCalendar cal = new MyCalendar(); MyCalendar.book(start, end)
示例:
MyCalendar();
MyCalendar.book(10, 20); // returns true
MyCalendar.book(50, 60); // returns true
MyCalendar.book(10, 40); // returns true
MyCalendar.book(5, 15); // returns false
MyCalendar.book(5, 10); // returns true
MyCalendar.book(25, 55); //returns true
解释:
前两个日程安排可以添加至日历中。
第三个日程安排会导致双重预订,但可以添加至日历中。
第四个日程安排活动(5,15)不能添加至日历中,因为它会导致三重预订。
第五个日程安排(5,10)可以添加至日历中,因为它未使用已经双重预订的时间10。
第六个日程安排(25,55)可以添加至日历中,因为时间[25,40] 将和第三个日程安排双重预订; 时间 [40,50] 将单独预订,时间 [50,55)将和第二个日程安排双重预订。
class MyCalendarTwo {
map <int, int> differ;
public:
MyCalendarTwo() {
}
bool book(int start, int end) {
differ[start]++;
differ[end]--;
int cur = 0;
for(auto mp : differ){
if(mp.first == end){
break;
}
cur += mp.second;
if(mp.first >= start){
if(cur >= 3){
//注意:当三重订单时需要删除当前日程安排,否则将因为误添加订单,导致后面的订单数计算有误
differ[start]--;
differ[end]++;
return false;
}
}
}
return true;
}
};
补充题:729. 我的日程安排表 I
实现一个 MyCalendar 类来存放你的日程安排。如果要添加的日程安排不会造成 重复预订 ,则可以存储这个新的日程安排。
当两个日程安排有一些时间上的交叉时(例如两个日程安排都在同一时间内),就会产生 重复预订 。
日程可以用一对整数 start 和 end 表示,这里的时间是半开区间,即 [start, end), 实数 x 的范围为, start <= x < end 。
实现 MyCalendar 类:
MyCalendar() 初始化日历对象。
boolean book(int start, int end) 如果可以将日程安排成功添加到日历中而不会导致重复预订,返回 true 。否则,返回 false 并且不要将该日程安排添加到日历中。
示例:
输入:
[“MyCalendar”, “book”, “book”, “book”]
[[], [10, 20], [15, 25], [20, 30]]
输出:
[null, true, false, true]
解释:
MyCalendar myCalendar = new MyCalendar();
myCalendar.book(10, 20); // return True
myCalendar.book(15, 25); // return False,这个日程安排不能添加到日历中,因为时间 15 已经被另一个日程安排预订了。
myCalendar.book(20, 30); // return True ,这个日程安排可以添加到日历中,因为第一个日程安排预订的每个时间都小于 20 ,且不包含时间 20 。
【分析】二分查找
按时间顺序维护日程安排,用 Set数据结构来保持元素排序和支持快速插入。
class MyCalendar {
//按时间顺序维护日程安排,则可以通过二分查找日程安排的情况来检查新日程安排是否可以预订
//需要一个数据结构能够保持元素排序和支持快速插入,可以用 Set 来构建
set<pair<int, int>> calendar;
public:
MyCalendar() {}
bool book(int start, int end) {
//每次查找起点大于等于 end 的第一个区间
//对于集合set而言没有下面这种用法
// auto it = lower_bound(calendar.begin(), calendar.end(), {end, 0});
//集合set需要这样调用二分查找函数
auto it = calendar.lower_bound({end, 0});
//同时紧挨着这个第一个区间的前一个区间的后端(注意不是前端)需要≤start
if(it == calendar.begin() || (--it)->second <= start){
calendar.insert({start, end});
return true;
}
return false;
}
};
线段树
除了查分数组之外,另一种维护区间更新的数据结构就是线段树,线段树除了可以快速的更新区间,还可以快速的查询区间最值。
由于普通的线段树需要开4n的空间,所以为了让数据离散化可以选择动态开点。并且根节点的值就是所有区间的最大值,通常来说,时间提升了不少但整体空间复杂度提升。
线段树最经典的应该是307.区域和检索。就是给你一个数组,会有简单的更新操作以及查询区域和的操作。查询操作指的是给你一个区间[L,R], 返回该区间[L,R]内所有元素的和。更新操作指的是,给你一个下标索引和一个值,将数组中该索引值对于的元素值改为新的给定值。
线段树(处理区域和查询问题):
对于查询区间和,我们容易想到的一个点就是使用前缀和,这样我们就可以将查询的操作提升到O(1), 但是使用前缀和会有一个问题,当我们的更新次数过多时,尤其是需要更新的元素比较靠前时,每一次更新的代价都会为O(n),从而没有达到优化的效果。但是对于元素不变动的数组前缀和还是有很不错的优势!
线段树将此类问题的查询以及更新的时间复杂度都变成了O(logn)。当进行多次查询与更新时,线段树一定比前缀和更具优势。
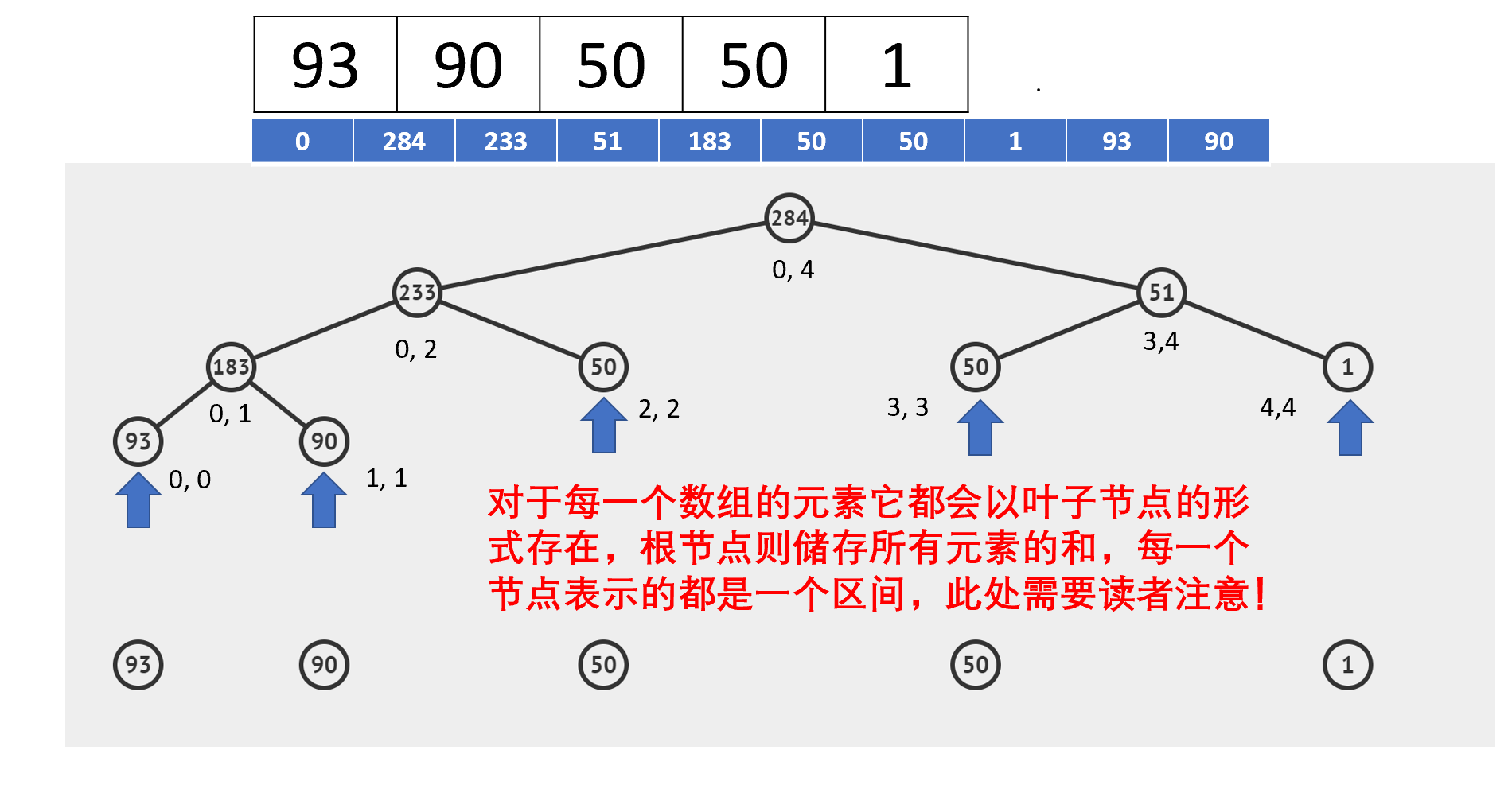
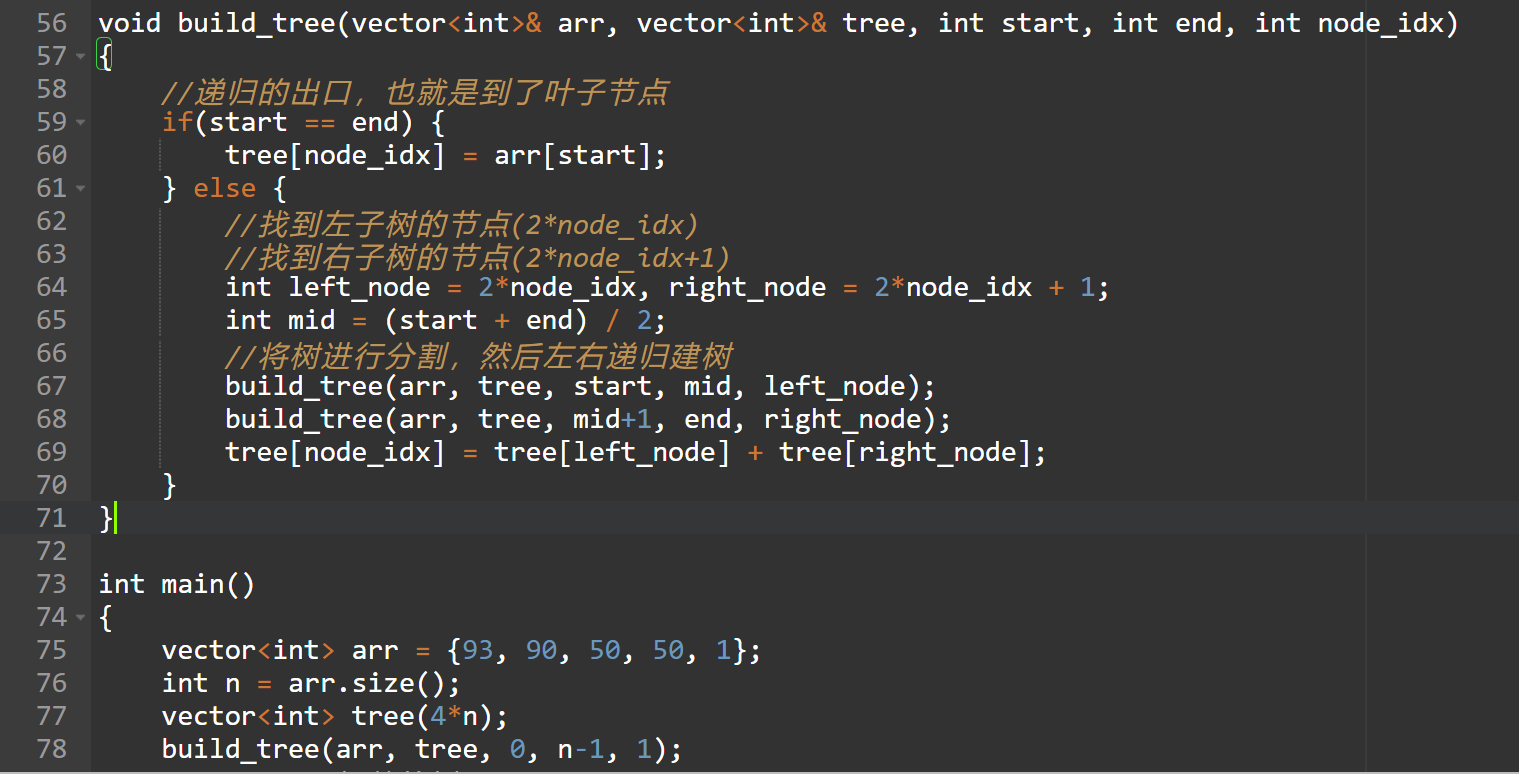
线段树的结构有点像堆,首先需要明确的是,我们用数组来表示树的结构,对于根树的根节点,它会在index=1的位置上(其实此处0也行,不过大家普遍用1,区别就是计算子节点的方式不同),然后对于其节点的左右子节点的下标分别为 2×index 与 2×index+1。然后其子节点也是这样的规律。
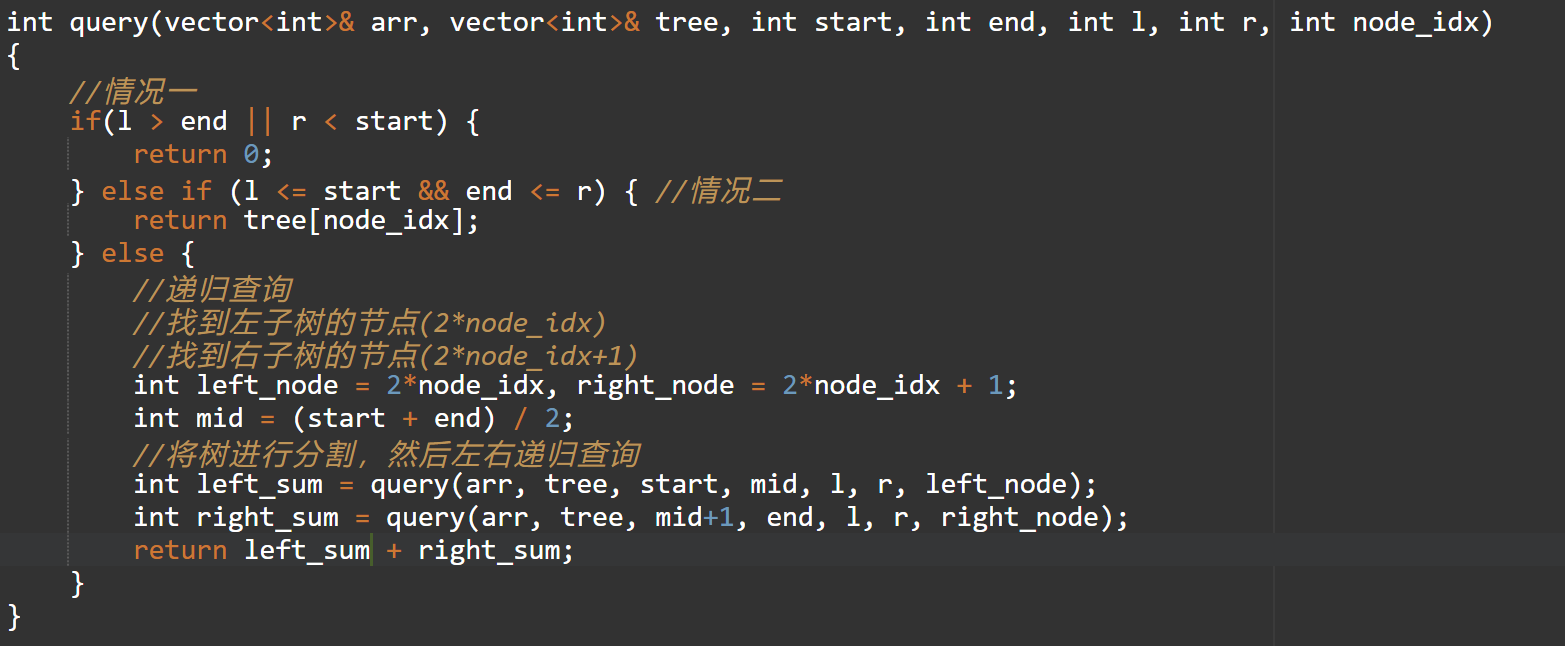
查询: 我们会根据区间从根节点向树的两边递归查寻。假设我们现在要查找此树的[2,4]的区间和,即[50,50,1]的和, 那么这个过程是什么样的呢?
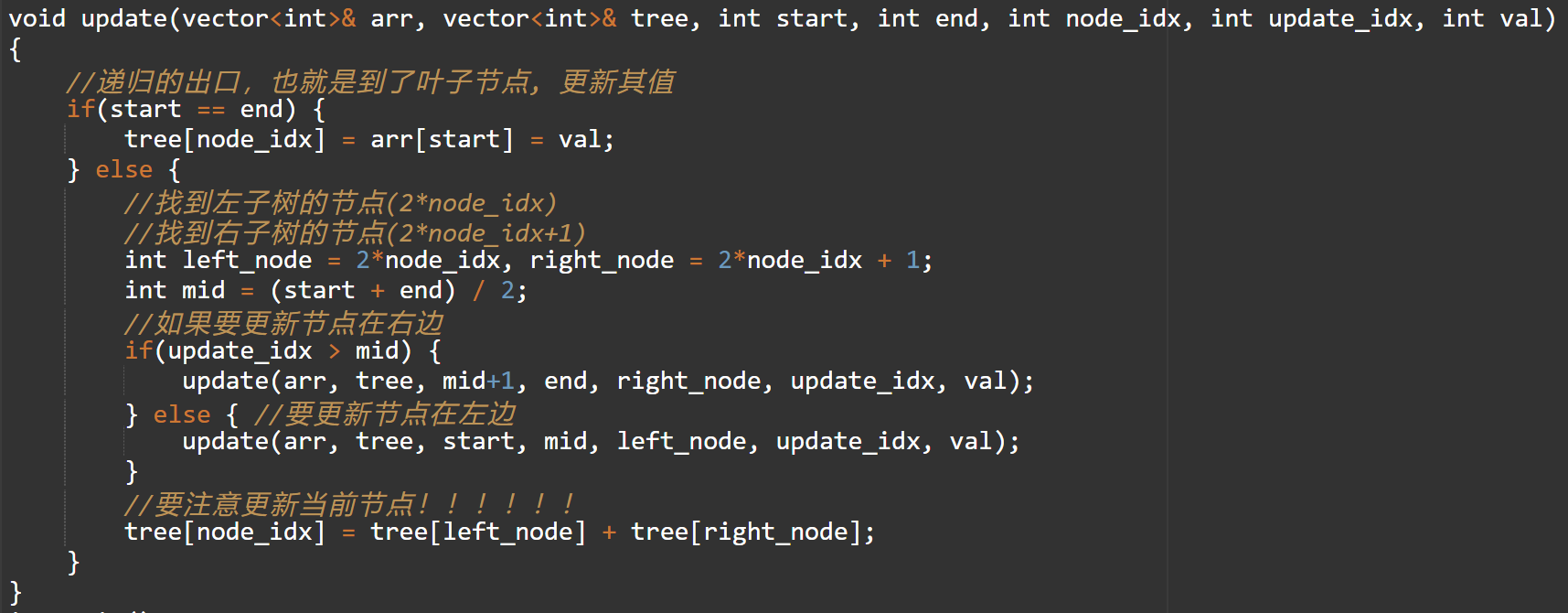
更新:假设我们要将其数组中的1更新为2,结构会发生什么变化?而有那些节点会做出改变呢?
到此我们已经基本了解了线段树了,我们发现线段树让更新与查询的时间复杂度都变成了O(logn), 下面我们来代码层面的学习一下线段树。
- 建树
-
跑完以上代码后,我们的线段树数组如下: (可以发现根节点在索引为1的位置的确为284,是所有元素的和,读者可以根据树的结构,以及从开头介绍的左右子节点的计算方式一一检查是否正确
- 检索
检索需要讨论以下情况:
情况一:
情况二:
情况二则是当前区间被我们的检索区间包围,即蓝色区间在绿色区间里面时,因此不必继续往下递归,可以直接返回当前节点值。这里比较容易想,读者可参考之前的线段树查询。思考一下,每一个节点表示的都是一个区间内所有元素的和,那么当整个当前区间都被我们的检索区间包围了,证明我们需要所有的元素,因此不必继续往下递归查询,可以返回其节点值。譬如之前例子中的区间[3,4],代码输出中依然可以观察到这一点。
代码如下:
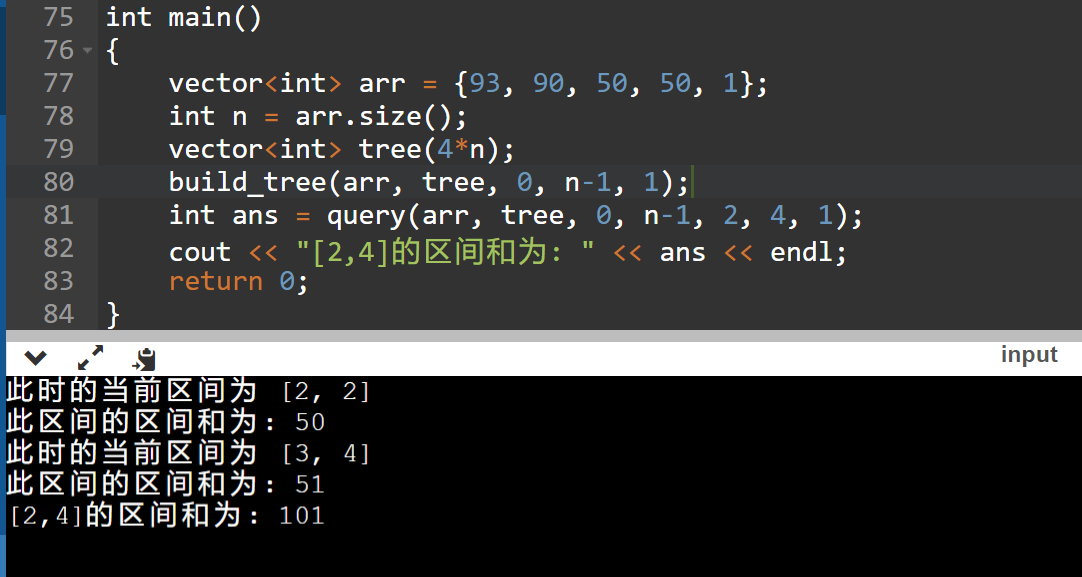
示例查询区间[2,4]的区域和结果如下: 50 + 50 + 1 = 101.为了可视化,我在其query方法中加入了几行输出。我们可以发现当递归到区间[3,4]时其实已经停止继续递归下去了,这正是我们想要的结果。
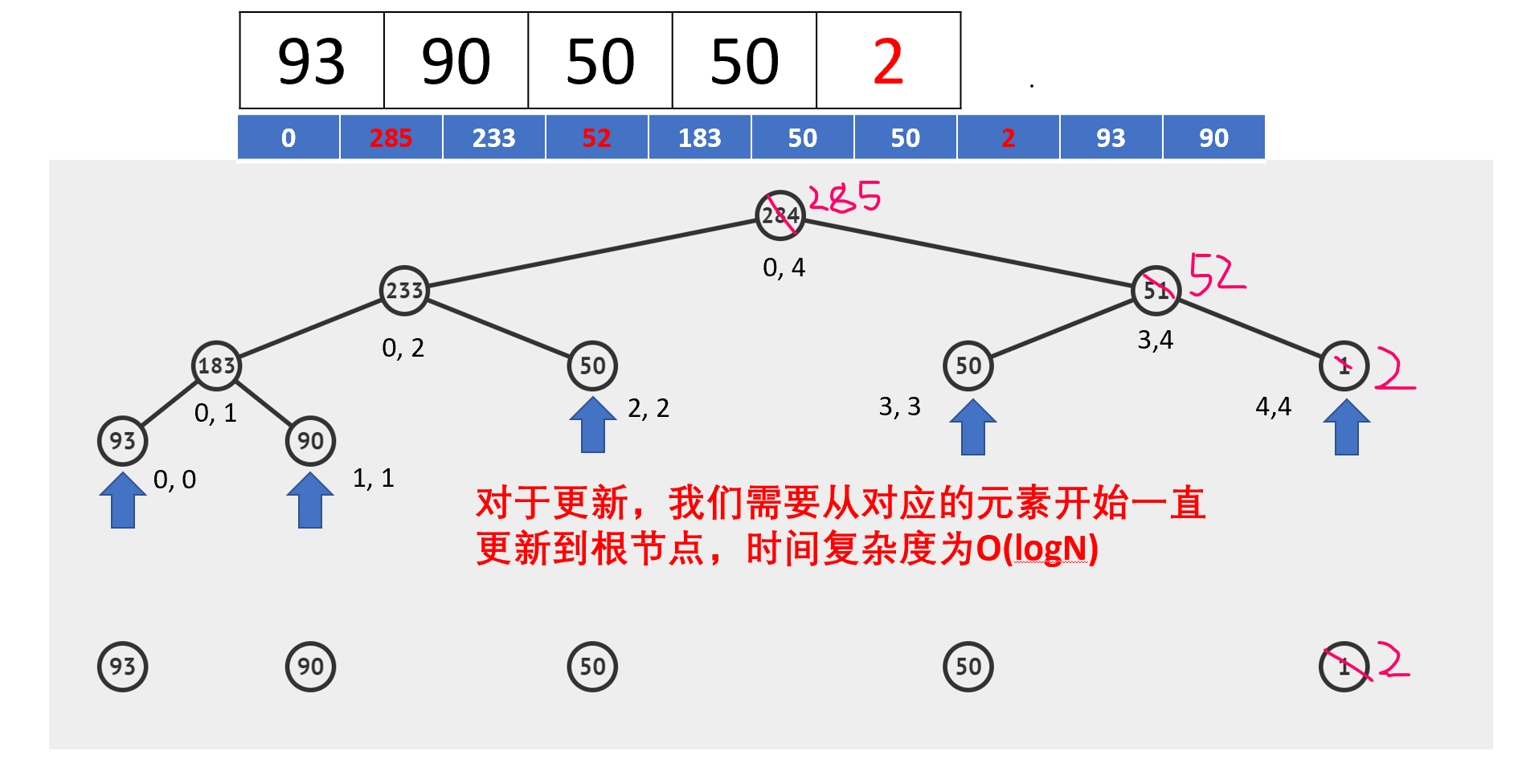
- 更新
更新与建树很像,当其递归到出口时就说明我们已经找到了要更新元素的节点。要注意更新完元素后,其包含此元素的区间节点都需要更新,代码中已加注释。
我们做一次更新,将数组从[93,90,50,50,1]改到[93,90,50,50,2],然后在做一次查询看结果是否正确:
题目练习:
732. 我的日程安排表 III
当 k 个日程安排有一些时间上的交叉时(例如 k 个日程安排都在同一时间内),就会产生 k 次预订。
给你一些日程安排 [start, end) ,请你在每个日程安排添加后,返回一个整数 k ,表示所有先前日程安排会产生的最大 k 次预订。
【问题解读】
首先我们来将问题转化一下,让题意更加明显,其实本题的本质就是给你一个区间,然后让你将其[start, end)内所有的元素值加上1,在进行了每一次的book更新的操作后,返回[0,
1
e
9
1e9
1e9]这个区间内的最大元素值是多少。
本题的解法本质上其实也是运用了线段树的思想,但是从检查区域和,变为了检索线段树中叶子节点的最大值是多少。我们很容易的想到,对于其一段区间我们需要book时,我们可以将其区间内的所有元素都加上1。显而易见的是,我们无法真的去建树,以及真的去更新其元素值。
对于第一个问题,由于此题的数据问题,我们可能造成内存溢出。因此我们用哈希表来表示我们的线段树,这样可以省去许多内存空间。
对于其第二个问题,不需要真的去手动更新每个节点值。我们选择的是官解中的懒标记,及如果当前节点区间的被索引的区间覆盖时,我们则将表示此区间的节点值加1,表示此区间内的所有元素值都加了一位,这里很重要,读者需要多读几遍。 个人觉得懒标记最难理解的地方就在这里,详细可看思路步骤中的第二点解读。
【思路步骤】
1.需要两个哈希表,一个用于线段树,一个用于区间的懒标记使用。注意此时的线段树的节点拥有的是该区间内的所有元素中的最大值。(不要被上述区间和的例子干扰,注意本题问的是什么!区间和提供的是思路!)
2.对于一个区间的更新,我们左右递归,下面分类讨论:
1)当该区间不在检索区间内时,则start > r || end < l,不做更新,直接返回。
2)当该区间被检索区间覆盖时,我们无需手动去更新该区间内所有元素值,只需要标记一下该区间内的所有元素都被加上了一位即可。显而易见,无论当前节点区间的最大值为多少,当该区间的所有元素值都加一时,其拥有的最大值自然也需要加一位。
3)当该区间内有元素不在其检索区间时,递归左右两边去更新我们的线段树。
3.返回根节点的最大值,即所有元素中的最大值。
class MyCalendarThree {
private:
unordered_map<int, int> tree;
unordered_map<int, int> lazy;
public:
MyCalendarThree() {
}
void update(int start, int end, int l, int r, int node)
{
if(start > r || end < l) {
return;
} else if(start <= l && r <= end) {
// 当前区间被检索区间覆盖, 因此区间内所有元素都加一
// 自然而然,无论当前节点区间的最大值为多少,当该区间的所有
// 元素值都加一时,其拥有的最大值自然也需要加一位
++tree[node];
++lazy[node];
} else {
int left_node = node*2, right_node = node*2 + 1;
int mid = (l+r) >> 1;
update(start, end, l, mid, left_node);
update(start, end, mid+1, r, right_node);
tree[node] = lazy[node] + max(tree[left_node], tree[right_node]);
}
}
int book(int start, int end) {
update(start, end-1, 0, 1e9, 1);
return tree[1];
}
};
复杂度分析
时间复杂度: O ( n log C ) O(n \log C) O(nlogC),其中 n 为日程安排的数量。由于使用了线段树查询,线段树的最大深度为 log C \log C logC, 每次最多会查询 log C \log C logC个节点,每次求最大的预定需的时间复杂度为 O ( log C + log C ) O(\log C + \log C) O(logC+logC),因此时间复杂度为 O ( n log C ) O(n \log C) O(nlogC),在此 C 取固定值即为 1 0 9 10^9 109。
空间复杂度: O ( n log C ) O(n \log C) O(nlogC),其中 n 为日程安排的数量。由于该解法采用的为动态线段树,线段树的最大深度为 log C \log C logC,每次预定最多会在线段树上增加 log C \log C logC个节点,因此空间复杂度为 O ( n log C ) O(n \log C) O(nlogC),在此 C 取固定值即为 1 0 9 10^9 109 。
前缀树/字典树(Trie)
前缀树(Trie Tree),Trie [traɪ] 读音和 try 相同,前缀树也叫字典树或单词查找树。
Trie(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
「前缀树」比较常用的应用场景:给定一个字符串集合构建一棵前缀树,然后给一个字符串,判断前缀树中是否存在该字符串或者该字符串的前缀。
Trie 是一种非典型的多叉树模型,多叉好理解,即每个结点的分支数量可能为多个。
为什么说非典型呢?因为它和一般的多叉树不一样,尤其在结点的数据结构设计上,比如一般的多叉树的结点是这样的:
struct TreeNode {
VALUETYPE value; //结点值
TreeNode* children[NUM]; //指向孩子结点
};
而 Trie 的结点是这样的(假设只包含’a’~'z’中的字符),可以理解为26叉树(有的分支为空,可以忽略):
struct TrieNode {
bool isEnd; //该结点是否是一个串的结束
vector<TrieNode*> children = vector<TrieNode*>(26);//字母映射表
//TrieNode* children[26]; //或者这样写
};
children 中保存了对当前结点而言下一个可能出现的所有字符的链接,因此我们可以通过一个父结点来预知它所有子结点的值:
for (int i = 0; i < 26; i++) {
char ch = 'a' + i;
if (parentNode->children[i] == nullptr) {
说明父结点的后一个字母不可为 ch
} else {
说明父结点的后一个字母可以是 ch
}
}
来看个例子,想象以下,包含三个单词 “sea”,“sells”,“she” 的 Trie 会长啥样呢?它的真实情况是这样的:
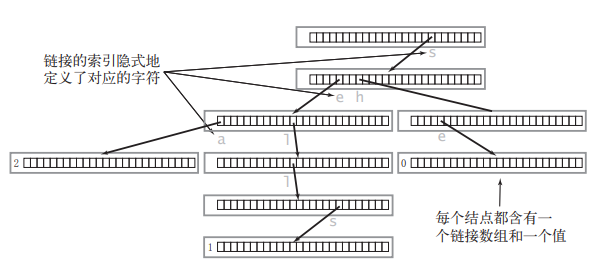
Trie 中一般都含有大量的空链接,因此在绘制一棵单词查找树时一般会忽略空链接,同时为了方便理解我们可以画成这样:
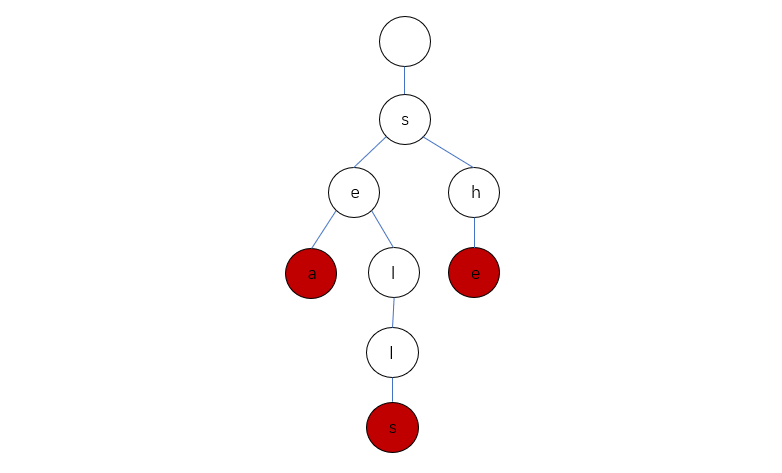
由于都是小写字母,所以对于每个节点,均有 26 个孩子节点,上图中没有画出来,省略了而已…,但是要记住:每个节点均有 26 个孩子节点
还有一个点要明确:节点仅仅表示从根节点到本节点的路径构成的字符串是否有效而已
对于上图中红色的节点,均为有效节点,即:从根节点到红色节点的路径构成的字符串均在集合中
接下来我们一起来实现对 Trie 的一些常用操作方法:
1.定义类 Trie
class Trie {
private:
bool isEnd;
vector<Trie*> children = vector<Trie*>(26);//字母映射表
public:
//方法将在下文实现...
};
2.插入
描述:向 Trie 中插入一个单词 word
实现:这个操作和构建链表很像。首先从根结点的子结点开始与 word 第一个字符进行匹配,一直匹配到前缀链上没有对应的字符,这时开始不断开辟新的结点,直到插入完 word 的最后一个字符,同时还要将最后一个结点isEnd = true;,表示它是一个单词的末尾。
void insert(string word) {
Trie* node = this;
for (char c : word) {
if (node->children[c-'a'] == nullptr) {
node->children[c-'a'] = new Trie();
}
node = node->children[c-'a'];
}
node->isEnd = true;
}
3.查找
描述:查找 Trie 中是否存在单词 word
实现:从根结点的子结点开始,一直向下匹配即可,如果出现结点值为空就返回 false,如果匹配到了最后一个字符,那我们只需判断 node->isEnd 即可。
bool search(string word) {
Trie* node = this;
for (char c : word) {
node = node->children[c - 'a'];
if (node == nullptr) {
return false;
}
}
return node->isEnd;
}
4.前缀匹配
描述:判断 Trie 中是或有以 prefix 为前缀的单词
实现:和 search 操作类似,只是不需要判断最后一个字符结点的isEnd,因为既然能匹配到最后一个字符,那后面一定有单词是以它为前缀的。
bool startsWith(string prefix) {
Trie* node = this;
for (char c : prefix) {
node = node->children[c-'a'];
if (node == nullptr) {
return false;
}
}
return true;
}
总结:
通过以上介绍和代码实现我们可以总结出 Trie 的几点性质:
1.Trie 的形状和单词的插入或删除顺序无关,也就是说对于任意给定的一组单词,Trie 的形状都是唯一的。
2.查找或插入一个长度为 L 的单词,访问 children 数组的次数最多为 L + 1 L+1 L+1,和 Trie 中包含多少个单词无关。
3.Trie 的每个结点中都保留着一个字母表,这是很耗费空间的。如果 Trie 的高度为 n n n,字母表的大小为 m m m,最坏的情况是 Trie 中还不存在前缀相同的单词,那空间复杂度就为 O ( m n ) O(m^n) O(mn)
最后,关于 Trie 的应用场景,希望你能记住 8 个字:一次建树,多次查询。(慢慢领悟叭~~)
请你实现 Trie 类:
Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
示例:
输入 [“Trie”, “insert”, “search”, “search”, “startsWith”, “insert”, “search”]
[[], [“apple”], [“apple”], [“app”], [“app”], [“app”],[“app”]]
输出 [null, null, true, false, true, null, true]
解释 Trie trie = new Trie();
trie.insert(“apple”);
trie.search(“apple”);// 返回 True
trie.search(“app”); // 返回 False
trie.startsWith(“app”);// 返回 True
trie.insert(“app”);
trie.search(“app”); // 返回 True
class Trie {
bool isend;
//若使用语句 vector<Trie*> children(26);
//编译器可能无法区分这是一个成员函数声明还是一个成员变量声明,也就是产生歧义。
//解决办法就是消除歧义,使用下面的方式即可
//vector<Trie*> children = vector<Trie*>(26);//明确这是一个成员变量声明
//或者去默认构造函数里面进行成员变量的初始化
vector<Trie*> children;
public:
//children 默认为空指针
Trie():children(26), isend(false) {}
void insert(string word) {
Trie* node = this;
for(char & ch : word){
if(node->children[ch - 'a'] == nullptr){ //容易漏 node->
node->children[ch - 'a'] = new Trie();
}
node = node->children[ch - 'a']; //没有else
}
node->isend = true;
}
bool search(string word) {
Trie* node = this;
for(char& ch : word){
node = node->children[ch - 'a'];
if(node == nullptr){
return false;
}
}
return node->isend;
}
bool startsWith(string prefix) {
Trie* node = this;
for(char& ch : prefix){
node = node->children[ch - 'a'];
if(node == nullptr){
return false;
}
}
return true;
}
};
前缀树例题整理:
208. 实现 Trie (前缀树)
单调栈
单调栈一般存储的是下标,满足从栈底到栈顶的下标对应的数组 中的元素递减。
判别是否需要使用单调栈,如果需要找到左/右边第一个比当前位置的数大/小的元素,则可以考虑使用单调栈;单调栈的题目如矩形求面积等等
739. 每日温度
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指在第 i 天之后,才会有更高的温度。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
【解答】用单调栈,每个元素最多出栈入栈一次
可以维护一个存储下标的单调栈,从栈底到栈顶的下标对应的温度列表中的温度依次递减。如果一个下标在单调栈里,则表示尚未找到下一次温度更高的下标。
正向遍历温度列表。对于温度列表中的每个元素,如果栈为空,则直接进栈;如果栈不为空,则与栈顶元素比较,若当前元素大于栈顶元素,则栈顶元素出栈,并更新等待天数,重复上述操作直到栈为空或者栈顶元素对应的温度小于等于当前温度,然后将 当前元素下标 i 进栈。
由于单调栈满足从栈底到栈顶元素对应的温度递减,因此每次有元素进栈时,会将温度更低的元素全部移除,并更新出栈元素对应的等待天数,这样可以确保等待天数一定是最小的。
vector<int> dailyTemperatures(vector<int>& temperatures) {
stack<int> st;
int n = temperatures.size();
vector<int> ans(n);
for(int i = 0; i < n; ++i){
while(!st.empty() && temperatures[i] > temperatures[st.top()]){
int k = st.top();
ans[k] = i - k;
st.pop();
}
st.emplace(i);
}
return ans;
}
42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组[0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
【分析】本题比较好记的是动态规划解法,详见动态规划专题
下面介绍单调栈解法:
维护一个单调栈,单调栈存储的是下标,满足从栈底到栈顶的下标对应的数组
height
\textit{height}
height 中的元素递减。
从左到右遍历数组,遍历到下标 i 时,如果栈内至少有两个元素,记栈顶元素为
top
\textit{top}
top,
top
\textit{top}
top 的下面一个元素是
left
\textit{left}
left,则一定有
height
[
left
]
≥
height
[
top
]
\textit{height}[\textit{left}] \ge \textit{height}[\textit{top}]
height[left]≥height[top] 。如果
height
[
i
]
>
height
[
top
]
\textit{height}[i]>\textit{height}[\textit{top}]
height[i]>height[top],则得到一个可以接雨水的区域,该区域的宽度是
i
−
left
−
1
i-\textit{left}-1
i−left−1,高度是
min
(
height
[
left
]
,
height
[
i
]
)
−
height
[
top
]
\min(\textit{height}[\textit{left}],\textit{height}[i])-\textit{height}[\textit{top}]
min(height[left],height[i])−height[top],根据宽度和高度即可计算得到该区域能接的雨水量。
为了得到 left \textit{left} left,需要将 top \textit{top} top 出栈。在对 top \textit{top} top 计算能接的雨水量之后, left \textit{left} left 变成新的 top \textit{top} top,重复上述操作,直到栈变为空,或者栈顶下标对应的 height \textit{height} height 中的元素大于或等于 height [ i ] \textit{height}[i] height[i]。
在对下标 i 处计算能接的雨水量之后,将 i 入栈,继续遍历后面的下标,计算能接的雨水量。遍历结束之后即可得到能接的雨水总量。
int trap(vector<int>& height) {
int ans = 0;
stack<int> stk;
int n = height.size();
for (int i = 0; i < n; ++i) {
while (!stk.empty() && height[i] > height[stk.top()]) {
int top = stk.top();
stk.pop();
if (stk.empty()) {
break;
}
int left = stk.top();
int currWidth = i - left - 1;
int currHeight = min(height[left], height[i]) - height[top];
ans += currWidth * currHeight;
}
stk.push(i);
}
return ans;
}
一个比较经典的单调栈题目:
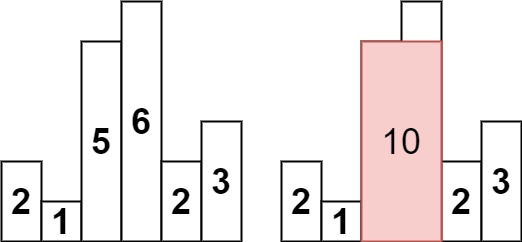
84. 柱状图中最大的矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
输入:
heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
示例 2:
输入:
heights = [2,4]
输出: 4
【分析】
枚举每一个柱形的「高」,使用一重循环枚举某一根柱子,将其固定为矩形的高度
h
h
h。随后我们从这跟柱子开始向两侧延伸,直到遇到左右两侧最近的高度小于
h
h
h 的柱子,这样这两根柱子之间(不包括其本身)的所有柱子高度均不小于
h
h
h,就确定了此固定高度矩形的左右边界。如果左右边界之间的宽度为
w
w
w,那么对应的面积为
w
×
h
w \times h
w×h。
求一根柱子的左/右侧且最近的小于其高度的柱子,可以用单调栈。
对于两根柱子
j
0
j_0
j0 以及
j
1
j_1
j1,如果
j
0
<
j
1
j_0 < j_1
j0<j1 并且
heights
[
j
0
]
≥
heights
[
j
1
]
\textit{heights}[j_0] \geq \textit{heights}[j_1]
heights[j0]≥heights[j1],那么对于任意的在它们之后出现的柱子
i
(
j
1
<
i
)
i(j_1 < i)
i(j1<i),
j
0
j_0
j0 一定不会是
i
i
i 左侧且最近的小于其高度的柱子。
步骤为:
栈中存放下标
j
j
j 值。从栈底到栈顶,
j
j
j 的值严格单调递增,同时对应的高度值也严格单调递增;
1)求一根柱子的左侧且最近的小于其高度的柱子:
当我们枚举到第
i
i
i 根柱子时,我们从栈顶不断地移除
height
[
j
]
≥
height
[
i
]
\textit{height}[j] \geq \textit{height}[i]
height[j]≥height[i] 的
j
j
j 值。在移除完毕后,栈顶的
j
j
j 值就一定满足
height
[
j
]
<
height
[
i
]
\textit{height}[j] < \textit{height}[i]
height[j]<height[i],此时
j
j
j 就是
i
i
i 左侧且最近的小于其高度的柱子。
这里会有一种特殊情况。如果我们移除了栈中所有的
j
j
j 值,那就说明
i
i
i 左侧所有柱子的高度都大于
height
[
i
]
\textit{height}[i]
height[i],那么我们可以认为
i
i
i 左侧且最近的小于其高度的柱子在位置
j
=
−
1
j=-1
j=−1,它是一根「虚拟」的、高度无限低的柱子。这样的定义不会对我们的答案产生任何的影响,我们也称这根「虚拟」的柱子为「哨兵」。
我们再将
i
i
i 放入栈顶。
2)同理,求一根柱子的右侧且最近的小于其高度的柱子时,只需要将「哨兵」换成 j = n j=n j=n ,从后往前遍历即可。
int largestRectangleArea(vector<int>& heights) {
int n = heights.size(), ans = 0;
stack<int> st;
//可以同时初始化两个同类型向量
vector<int> left(n), right(n);
//求一根柱子的左侧且最近的小于其高度的柱子下标,从前往后遍历
for(int i = 0; i < n; ++i){
while(!st.empty() && heights[st.top()] >= heights[i]){
st.pop();
}
if(st.empty()){
left[i] = -1;
}else{
left[i] = st.top();
}
st.push(i);
}
//对栈重新初始化,清空之前存的元素
st = stack<int>();
//求一根柱子的右侧且最近的小于其高度的柱子下标,从后往前遍历
for(int i = n - 1; i >= 0; --i){
while(!st.empty() && heights[st.top()] >= heights[i]){
st.pop();
}
if(st.empty()){
right[i] = n;
}else{
right[i] = st.top();
}
st.push(i);
}
for(int i = 0; i < n; ++i){
ans = max(ans, (right[i] - left[i] - 1) * heights[i]);
}
return ans;
}
【方法优化】单调栈 + 常数优化
我们在对位置
i
i
i 进行出栈操作时其实就可以确定它的右边界!只遍历一遍即可。
当位置 i i i 被弹出栈时,说明此时遍历到的位置 i 0 i_0 i0 的高度小于等于 height [ i ] \textit{height}[i] height[i],并且在 i 0 i_0 i0 与 i i i 之间没有其他高度小于等于 height [ i ] \textit{height}[i] height[i] 的柱子。这是因为,如果在 i i i 和 i 0 i_0 i0 之间还有其它位置的高度小于等于 height [ i ] \textit{height}[i] height[i] 的,那么在遍历到那个位置的时候, i i i 应该已经被弹出栈了。所以位置 i 0 i_0 i0 就是位置 i i i 的右边界。
需要思考的是,我们需要的是「一根柱子的左侧且最近的小于其高度的柱子」,但这里我们求的是小于等于,这就会导致我们确实无法求出正确的右边界,但对最终的答案没有任何影响。这是因为在答案对应的矩形中,如果有若干个柱子的高度都等于矩形的高度,那么最右侧的那根柱子是可以求出正确的右边界的,而我们没有对求出左边界的算法进行任何改动,因此最终的答案还是可以从最右侧的与矩形高度相同的柱子求得的。虽然相同高度柱子其他位置求得的面积可能不对,但是我们保证相同高度最右侧柱子求得的最大面积是对的就可以了。
在遍历结束后,栈中仍然有一些位置,这些位置对应的右边界就是位置为 n n n 的「哨兵」。我们可以将它们依次出栈并更新右边界,也可以在初始化右边界数组时就将所有的元素的值置为 n n n。
int largestRectangleArea(vector<int>& heights) {
int n = heights.size(), ans = 0;
vector<int> left(n), right(n, n);
stack<int> st;
//一遍遍历,用单调栈同时求得左侧最近的低柱 和 右侧最近的相同高度或更高的高柱
for(int i = 0; i < n; ++i){
while(!st.empty() && heights[st.top()] >= heights[i]){
right[st.top()] = i;
st.pop();
}
left[i] = st.empty() ? -1 : st.top();
st.push(i);
}
//遍历不同的高度
for(int i = 0; i < n; ++i){
ans = max(ans, (right[i] - left[i] - 1) * heights[i]);
}
return ans;
}
每一个位置只会入栈一次(在枚举到它时),并且最多出栈一次。所以单调栈的总时间复杂度为 O ( N ) O(N) O(N)。
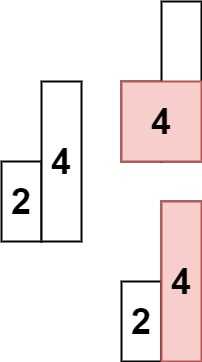
上一题的升级拓展题:
85. 最大矩形
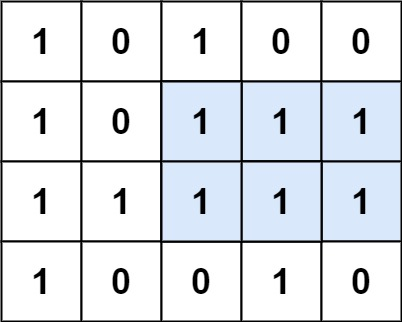
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例 1:
输入:
matrix =[[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出:6
解释:最大矩形如上图所示。
【分析】将输入矩阵转化为柱状图 + 单调栈优化求解
将输入矩阵转化为柱状图:
首先计算出矩阵的每个元素的左边连续 1 的数量,使用二维数组 left \textit{left} left 记录,其中 left [ i ] [ j ] \textit{left}[i][j] left[i][j] 为矩阵第 i i i 行第 j j j 列元素的左边连续 1 (包括自身)的数量,也就是按行统计到每个位置为止的连续1数量。这样实际上就将输入转化成了一系列的柱状图(每一列的 left \textit{left} left 向量值就对应了上一题的输入柱状图)。
随后,对于矩阵中任意一个点,我们枚举以该点为右下角的全 1 矩形。由于刚才相当于将输入矩阵拆分成了一列列的柱状图。因此,为了计算矩形的最大面积,我们只需要计算每列对应的柱状图中的最大面积,并找到全局最大值。
单调栈优化求解:
对于每一列生成的柱状图,可以使用上一题中基于柱状图的单调栈方法求解最大面积。
注意点,传入的参数矩阵是char类型,‘0’ ≠ 0。
int maximalRectangle(vector<vector<char>>& matrix) {
//首先计算出矩阵的每个元素的左边连续 1 的数量,使用二维数组 left 记录,
//其中 left[i][j] 为矩阵第 i 行第 j 列元素的左边连续 1 的数量。
int m = matrix.size();
if(m == 0) return 0;
int n = matrix[0].size();
vector<vector<int>> left(m, vector<int>(n));
for(int i = 0; i < m; ++i){
for(int j = 0; j < n; ++j){
if(matrix[i][j] == '1'){
left[i][j] = (j == 0 ? 1 : left[i][j - 1] + 1);
}
}
}
//对于矩阵中任意一个点,我们枚举以该点为右下角的全 1 矩形
//由于刚才相当于将输入矩阵拆分成了一列列的柱状图。因此,为了计算矩形的最大面积,
//我们只需要计算每列对应的柱状图中的最大面积,并找到全局最大值。
int ans = 0;
// 对于每一列,使用上一题中基于柱状图的单调栈方法求解最大面积
//每一列从上到下相当于从左到右
for(int j = 0; j < n; ++j){
vector<int> l(m, -1), r(m, m); //m
stack<int> st;
for(int i = 0; i < m; ++i){
while(!st.empty() && left[st.top()][j] >= left[i][j]){
r[st.top()] = i;
st.pop();
}
if(!st.empty()){
l[i] = st.top();
}
//或者 l[i] = (st.empty() ? -1 : st.top()); 可以不用初始化向量 l的值为 -1
st.push(i);
}
for(int i = 0; i < m; ++i){
ans = max(ans, (r[i] - l[i] - 1) * left[i][j]);
}
}
return ans;
}
此外,在得到 left \textit{left} left 数组之后,该题还可以采用暴力解法:
求解最大面积时,分别以每个元素为右下角,向上遍历不同的高度(遇到0停止),不同高度对应不同的宽度(一直取宽度的min),可以得到不同的面积,保存最大的面积。如下图:
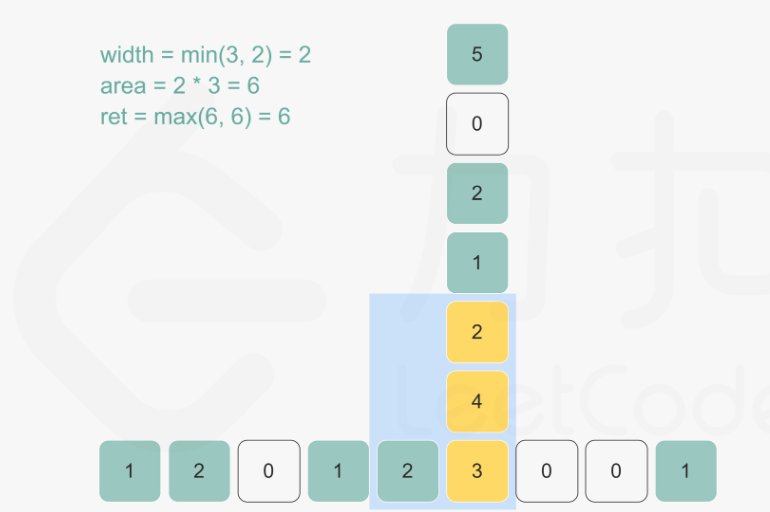
由于前面求 left \textit{left} left 数组的方式相同,下面代码只展示了优化暴力求解的部分。
int ans = 0;
for(int i = 0; i < m; ++i){
for(int j = 0; j < n; ++j){
int l = left[i][j], h = 0;
for(int k = i; k >= 0; --k){
if(left[k][j] == 0){
break;
}else{
l = min(l, left[k][j]);
h ++;
ans = max(l * h, ans);
}
}
}
}
return ans;
单调队列
单调队列用满足单调性的双端队列来实现,常用于求解每次滑动窗口中的最大值问题。
单调队列和单调栈都是存储的输入数组的下标。比如单调队列中保存的是一些单调递增的下标,但是这些下标对应的数组元素的值却呈现单调递减。
以一个经典题目为例:
239. 滑动窗口最大值
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口 k 内的数字。滑动窗口每次只向右移动一位。
返回滑动窗口最大值。
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
【思路】方法一:优先级队列
朴素思路:建立一个最大堆,每次读入一个新的数字,就把不在区间范围内的数字从堆中移除,然后堆的顶部就是此次循环的结果。
实现方式:初始时,将数组 nums \textit{nums} nums 的前 k k k 个元素放入优先队列中。每当我们向右移动窗口时,我们就可以把一个新的元素放入优先队列中,此时堆顶的元素就是堆中所有元素的最大值。然而这个最大值可能并不在滑动窗口中,在这种情况下,这个值在数组 nums \textit{nums} nums 中的位置出现在滑动窗口左边界的左侧。因此,当我们后续继续向右移动窗口时,这个值就永远不可能出现在滑动窗口中了,我们可以将其永久地从优先队列中移除。
我们不断地移除堆顶的元素,直到其确实出现在滑动窗口中。此时,堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素与滑动窗口的位置关系,我们可以在优先队列中存储二元组 ( num , index ) (\textit{num}, \textit{index}) (num,index),表示元素 num \textit{num} num 在数组中的下标为 index \textit{index} index。
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n = nums.size();
//pair<int, int>可以作为基本数据类型存储,不用建立结构体
priority_queue<pair<int, int>> q;
for (int i = 0; i < k; ++i) {
q.emplace(nums[i], i);
}
//注意优先级队列只有 top,没有 front
vector<int> ans = {q.top().first};
for (int i = k; i < n; ++i) {
q.emplace(nums[i], i);
while (q.top().second <= i - k) {
q.pop();
}
ans.push_back(q.top().first);
}
return ans;
}
时间复杂度: O ( n log n ) O(n \log n) O(nlogn)
方法二:利用双端队列构造单调队列(推荐这个方法!!)
顺着方法一的思路继续进行优化。
假设当前的滑动窗口中有两个下标
i
i
i 和
j
j
j,其中
i
i
i 在
j
j
j 的左侧(
i
<
j
i < j
i<j),并且
i
i
i 对应的元素不大于
j
j
j 对应的元素(
nums
[
i
]
≤
nums
[
j
]
\textit{nums}[i] \leq \textit{nums}[j]
nums[i]≤nums[j]),那么当滑动窗口向右移动时,只要
i
i
i 还在窗口中,那么
j
j
j 一定也还在窗口中,这是
i
i
i 在
j
j
j 的左侧所保证的。因此,由于
nums
[
j
]
\textit{nums}[j]
nums[j] 的存在,
nums
[
i
]
\textit{nums}[i]
nums[i] 一定不会是滑动窗口中的最大值了,我们可以将
nums
[
i
]
\textit{nums}[i]
nums[i] 永久地移除。
因此我们可以使用一个队列存储所有还没有被移除的下标。在队列中,这些下标按照从小到大的顺序被存储,并且它们在数组 nums \textit{nums} nums 中对应的值是严格单调递减的。因为如果队列中有两个相邻的下标,它们对应的值相等或者递增,那么令前者为 i i i,后者为 j j j,就对应了上面所说的情况,即 nums [ i ] \textit{nums}[i] nums[i] 会被移除,这就产生了矛盾。
当滑动窗口向右移动时,我们需要把一个新的元素放入队列中。为了保持队列的性质,我们会不断地将新的元素与队尾的元素相比较,如果前者大于等于后者,那么队尾的元素就可以被永久地移除,我们将其弹出队列。我们需要不断地进行此项操作,直到队列为空或者新的元素小于队尾的元素。
由于队列中下标对应的元素是严格单调递减的,因此队首下标对应的元素就是滑动窗口中的最大值。但与方法一中相同的是,此时的最大值可能在滑动窗口左边界的左侧,并且随着窗口向右移动,它永远不可能出现在滑动窗口中了。因此我们还需要不断从队首弹出元素,直到队首元素在窗口中为止。
为了可以同时弹出队首和队尾的元素,我们需要使用双端队列。满足这种单调性的双端队列一般称作「单调队列」。
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n = nums.size();
deque<int> q;
for(int i = 0; i < k; ++i){
while(!q.empty() && nums[i] >= nums[q.back()]){
q.pop_back();
}
q.push_back(i);
}
vector<int> ans = {nums[q.front()]};
for(int i = k; i < n; ++i){
while(!q.empty() && nums[i] >= nums[q.back()]){
q.pop_back();
}
q.push_back(i);
while(q.front() <= i - k){
q.pop_front();
}
ans.emplace_back(nums[q.front()]);
}
return ans;
}
每一个下标恰好被放入队列一次,并且最多被弹出队列一次,因此时间复杂度为 O ( n ) O(n) O(n)。
并查集
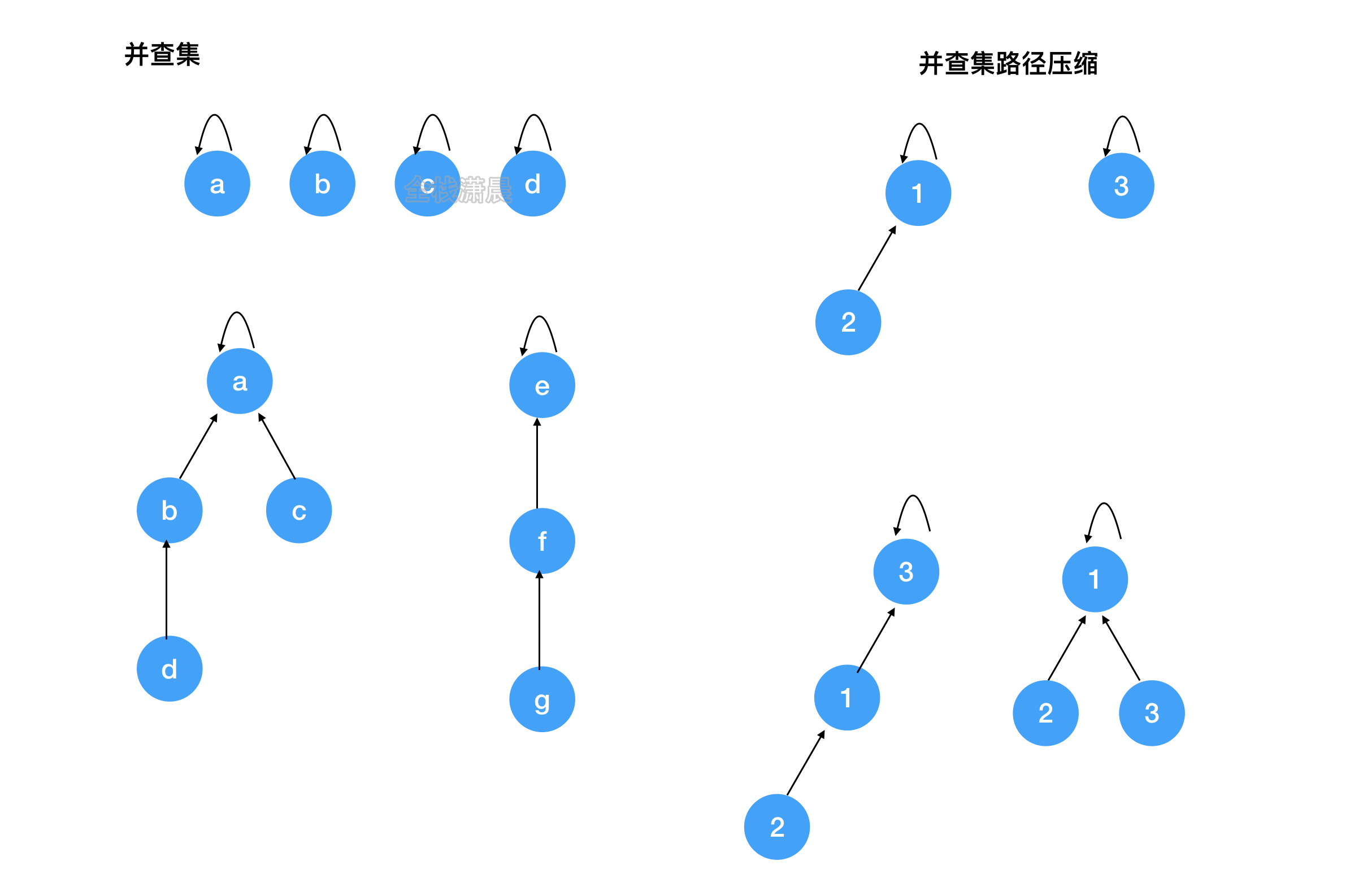
并查集(union & find):用于处理一些元素的合并和查询问题
Find:确定元素属于哪一个子集,他可以被用来确定两个元素是否属于同一个子集,加入路径压缩,复杂度近乎O(1)
Union:将两个子集合并成同一个集合
【附】全栈视频教程
方法一:深度优先搜索
将二维网格看成一个无向图,竖直或水平相邻的 1 之间有边相连。
为了求出岛屿的数量,我们可以扫描整个二维网格。如果一个位置为 1,则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中,每个搜索到的 1 都会被重新标记为 0。
最终岛屿的数量就是我们进行深度优先搜索的次数。
代码讲解
参考岛屿问题的模板解法
方法二:并查集
使用并查集代替搜索。
为了求出岛屿的数量,我们可以扫描整个二维网格。如果一个位置为 1,则将其与相邻四个方向上的 1 在并查集中进行合并。
最终岛屿的数量就是并查集中连通分量的数目。
需要一个类 :并查集类。其中定义三个私有变量: 一个是parent ,记录当前位置节点对应的父亲节点 ;一个是rank类,其记录了当前是根节点时树的深度,以此优化路径;最后是count,记录当前有多少个集合。
方法需要三个:一个是初始化,因为私有变量定义的是vector,所以要遍历数据 对vector进行pushback操作,然后是find和merge函数,merge函数只有再二者rank相同时会导致树深度加一, find函数则是顺便起到了扁平化的作用
//并查集
class UnionFind {
private:
vector<int> parent;
vector<int> rank;
int count; //并查集总数
public:
UnionFind(vector<vector<char>>& grid) {
count = 0;
int m = grid.size();
int n = grid[0].size();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == '1') {
parent.push_back(i * n + j);
++count;
}
else {
parent.push_back(-1);
}
rank.push_back(0);
}
}
}
//找当前位置节点对应的父亲节点(集合查找)
int find(int i) {
if (parent[i] != i) {
parent[i] = find(parent[i]);
}
return parent[i];
}
//集合合并
void unite(int x, int y) {
int rootx = find(x);
int rooty = find(y);
if (rootx != rooty) {
if (rank[rootx] < rank[rooty]) {
swap(rootx, rooty);
}
parent[rooty] = rootx;
if (rank[rootx] == rank[rooty]) rank[rootx] += 1;
--count;
}
}
//返回子集个数
int getCount() const {
return count;
}
};
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
int nr = grid.size();
if (!nr) return 0;
int nc = grid[0].size();
UnionFind uf(grid);
int num_islands = 0;
for (int r = 0; r < nr; ++r) {
for (int c = 0; c < nc; ++c) {
if (grid[r][c] == '1') {
grid[r][c] = '0';
if (r - 1 >= 0 && grid[r-1][c] == '1') uf.unite(r * nc + c, (r-1) * nc + c);
if (r + 1 < nr && grid[r+1][c] == '1') uf.unite(r * nc + c, (r+1) * nc + c);
if (c - 1 >= 0 && grid[r][c-1] == '1') uf.unite(r * nc + c, r * nc + c - 1);
if (c + 1 < nc && grid[r][c+1] == '1') uf.unite(r * nc + c, r * nc + c + 1);
}
}
}
return uf.getCount();
}
};
二叉树
二叉树的结构体定义常常如下:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
和类class的用法类似,常用的创建对象指针的方法为:
//创建指向结构体或对象的指针
TreeNode* node = new TreeNode(x);
比如类的定义与对象创建的定义为:
class Num{
private:
vector<string> res;
public:
Num():res({"abs", "d"}){} //默认构造函数初始化
//变换构造函数初始化
Num(vector<string> res){ //:res(res) 可以直接初始化列表给数据成员初始化
//res = this->res;注意this指针指向当前对象数据成员而不是形参,别用反了
this->res = res;
}
void disp(){
for(string& str : res){
cout<<str<<endl;
}
}
};
int main(){
//调用变换构造函数
Num t({"apple", "banana"});
t.disp(); //apple banana
//利用变换构造函数生成指向类对象的指针
Num *r = new Num({"a", "b", "c"});
r->disp(); // a b c
//调用默认构造函数
//调用默认构造函数时候不需要加()
//注意区分:与 Num* m = new Num() 需要加()不同
Num m;
m.disp(); //abs d
return 0;
}
需要理清楚几点:
1)struct 默认为 public 类型,而 class 默认为 private 类型。
2)this指针指向的是当前类对象,如果想给当前对象中定义的数据成员进行赋值,需要放到赋值号左边。比如this->res = res;中,左边的res是类数据成员,右边的res是传入构造函数的形参。当数据成员名与构造函数传入的形参名相同时,必须要用this指针,否则系统无法调用数据成员。
当数据成员名(比如改为red)与形参名不同时,可以不用this指针。直接red = res;进行初始化即可。
3)此外还可采用初始化列表的方式直接进行数据成员初始化,即使数据成员与形参名相同时也可以。
比如用变换构造函数初始化:
Num(vector<string> res):res(res){}
或者用默认构造函数初始化
Num():res({"abs", "d"}){}
创建二叉树
LeetCode中经常有函数参数是树的根结点root,做多了往往会觉得习以为常,认为题目理所应当会给创建好树,但是当笔试时候往往是白板,什么都没有的情况下就需要自己手动去建立一棵树,下面这段代码就会显得非常实用了。
根据层次遍历向量数组创建二叉树,空节点在数组中用-1表示:
//想改变指针而不是改变指针指向的值,需要传入指针的引用
//递归调用,传入初始根结点,数组以及当前节点下标
void buildTree(TreeNode* &root, vector<int>& nums, int i){ //注意root必须要加&
if(i<nums.size(){
TreeNode* node = new TreeNode(nums[i]);
root = node;
}
int left = 2*i+1;
int right = 2*i+2;
if(left<nums.size() && nums[left]!=-1){
buildTree(root->left, nums,left);
}
if(right<nums.size() && nums[right]!=-1){
buildTree(root->right, nums,right);
}
}
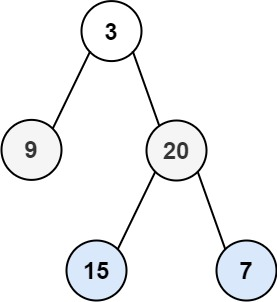
另外一种比较常用的写法,一个节点一个节点地输入数据:
比如下图的输入样例为:3 9 null null 20 15 null null 7 null null
struct TreeNode{
int val;
TreeNode* left, *right;
TreeNode():val(0), left(nullptr), right(nullptr){}
explicit TreeNode(int x):val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode* left, TreeNode* right):val(x), left(left), right(right) {}
};
//创建二叉树
TreeNode* CreateTree()
{
string str; cin>>str;
if (str == "null") return nullptr;
else {
auto* T = new TreeNode(stoi(str));
T->left = CreateTree();
T->right = CreateTree();
return T;
}
}
int main(){
printf("请采用先序遍历输入(空节点为null):\n");
TreeNode* root = CreateTree();
}
二叉树的遍历
先序遍历:先遍历根结点,再左子树、右子树
中序遍历:先左子树,再根结点,再右子树
后序遍历;先左子树,再右子树,最后根结点
这三种遍历都是用递归或栈实现。
层次遍历用队列实现。
给定二叉树的任何一种遍历序列,都无法唯一确定相应的二叉树。但是如果给定二叉树的中序遍历序列和任意的另一种遍历序列,就可以唯一地确定二叉树。
二叉树的递归遍历很简单,以前序遍历为例,稍微调整下面递归函数主体中三个语句的顺序就可以变为中序遍历或者后序遍历。但是不适用于层次遍历,层次遍历需要用队列非递归实现。
vector<int> ans;
void preOrder(TreeNode* root){
if(!root){
return ;
}
ans.emplace_back(root->val);
preOrder(root->left);
preOrder(root->right);
}
vector<int> preorderTraversal(TreeNode* root) {
preOrder(root);
return ans;
}
102. 二叉树的层序遍历
用队列实现二叉树的层次遍历:
按层输出,需要记录每层节点数。每次记录一下队列中的元素数目,作为循环中的当前层节点总数。
//二叉树层次遍历
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ans;
queue<TreeNode*> myQueue;//辅助队列,用于层次遍历
if (!root) {
return ans;
}
myQueue.emplace(root);
TreeNode *p = NULL;
while (!myQueue.empty()) {
int n = myQueue.size();//此时栈的大小(即将访问的层的节点数目)
vector<int> rec; //前往不要初始化大小n,否则后面emplace_back就会在n个0之后继续添加元素
for (int i = 0; i < n; ++i) {//将此层的所有节点出队列
p = myQueue.front();//获取队头
myQueue.pop();
rec.push_back(p->val);//记录val值
if (p->left ) {//放置左子树根节点
myQueue.push(p->left);
}
if (p->right) {//放置右子树根节点
myQueue.push(p->right);
}
}
ans.push_back(rec);//将此层的val结果放入结果容器
}
return ans;
}
};
树的深度优先搜索,用栈实现:
//力扣199. 二叉树的右视图
//树的深度优先搜索,用栈实现。
//深度优先遍历
void depthFirstSearch(Tree root){
stack<Node *> nodeStack; //使用C++的STL标准模板库
nodeStack.push(root);
Node *node;
while(!nodeStack.empty()){
node = nodeStack.top();
printf(format, node->data); //遍历根结点
nodeStack.pop();
if(node->rchild){
nodeStack.push(node->rchild); //先将右子树压栈
}
if(node->lchild){
nodeStack.push(node->lchild); //再将左子树压栈
}
}
}
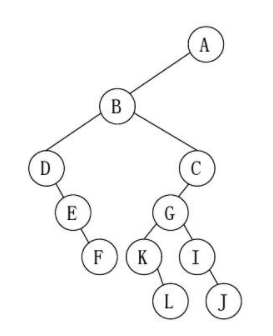
二叉树用栈实现的三种深度优先遍历可以采用这种树形的ABDEF路线来帮助理解:
先序遍历:ABDEFCGKLIJ
中序遍历:DEFBKLGIJCA
后序遍历:FEDLKJIGCBA
94. 二叉树的中序遍历
非递归的中序遍历,中序遍历比较常用,比如二叉搜索树的中序遍历就是个递增序列。用栈实现:
依次入栈到最左下节点D,然后开始出栈输出当前节点D,并转而指向当前左下节点D的右孩子E
//非递归的中序遍历,依次入栈到最左下节点D,然后开始出栈输出当前节点
//并转而指向当前左下节点D的右孩子E
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ans;
stack<TreeNode*> mystack;
while(root || !mystack.empty())
{
while(root)
{
mystack.emplace(root);
root=root->left;
}
root = mystack.top();
mystack.pop();//别忘了出栈,不然超出时间限制
ans.emplace_back(root->val);
root= root->right;
}
return ans;
}
144. 二叉树的前序遍历
非递归的先序遍历,用栈实现:
沿着左下路线入栈一个节点则输出一个节点,直到左下叶子D,然后转而指向左下节点D的右孩子E
//非递归的先序遍历,沿着左下路线入栈一个节点则输出一个节点,直到左下叶子D
//然后转而指向左下节点D的右孩子E
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ans;
stack<TreeNode*> mystack;
while(root || !mystack.empty())
{
while(root) //入栈一个节点则记录或输出一个节点,边入栈边输出
{
mystack.emplace(root);
ans.emplace_back(root->val);
root = root->left;
}
root = mystack.top();
mystack.pop();
root = root->right;
}
return ans;
}
145. 二叉树的后序遍历
非递归的后序遍历,后序遍历最难,因为要用pre指针记录之前出栈的右孩子,用栈实现:
【难点】考虑右下方一串光秃秃的右孩子情况,需要对已经遍历的右孩子进行pre标记,并需要将pre进行更新,以及将root置为空节点!否则root指向当前结点,之后又会进行一次重复的while压栈。
此外有右孩子的情况需要用else,因为另外一种情况也包括右孩子存在的情况,只不过那个情况的右孩子被pre标记输出过而已。
【过程】沿着左下路线依次入栈节点,到头后出栈当前左下叶子节点。当前节点有右孩子则转而指向右孩子;当前节点没有右孩子则输出当前节点并用pre记录,转而指向空节点,方便出栈下一个节点,或者当前节点的右孩子之前已经被记录输出过,则右孩子不再重复入栈,输出当前节点并用pre记录,转向空节点,继续出栈下一个节点。
//后序遍历二叉树
//沿着左下路线依次入栈节点,到头后出栈当前左下叶子节点
//当前节点有右孩子则转而指向右孩子
//当前节点没有右孩子则输出当前节点并用pre记录,转而指向空节点,方便出栈下一个节点
//或者当前节点的右孩子之前已经被记录输出过,则右孩子不再重复入栈,输出当前节点并用pre记录,转向空节点,继续出栈下一个节点
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ans;
stack<TreeNode*> mystack;
TreeNode* pre;
while(root || !mystack.empty())
{
while(root)
{
mystack.emplace(root);
root = root->left;
}
root = mystack.top();
//当没有右孩子时候需要输出当前节点(右叶子节点),
//或者当前节点的右孩子之前已经输出过了,用pre记录过已经输出的右孩子节点。
//否则的话因为判断到有右孩子,还会继续将右孩子入栈,然后将右孩子出栈输出,再出栈当前节点,陷入死循环
//考虑右下方一串光秃秃的右孩子情况,需要对已经遍历的右孩子进行pre标记
//并需要将pre进行更新,以及将root置为空节点!
//否则root指向当前结点,之后又会进行一次重复的while压栈
if(!root->right || root->right == pre)
{
ans.emplace_back(root->val);
mystack.pop();
pre = root;
root = nullptr;
}
//易错点:需要用else,因为上面那种情况也包括右孩子存在的情况
else
{
root = root->right;
}
}
return ans;
}
总结:
这三种遍历的非递归方式可以说是有一套模板,只是细微逻辑需要理解,模板大框架如下:
vector<int> traversal(TreeNode* root) {
vector<int> ans;
stack<TreeNode*> mystack;
TreeNode* pre; //仅后序遍历需要一个额外记录指针pre
while(root || !mystack.empty())
{
while(root) //仅前序遍历还需要边入栈边输出,其他两种遍历都是一直入栈到最左下节点
{
先序遍历:ans.emplace_back(root->val);//该句是先序遍历专有
mystack.emplace(root);
root = root->left;
}
root = mystack.top();
mystack.pop();
……下面三种遍历方法开始出现不同:
先序遍历直接转向右孩子:root = root->right; //先序
中序遍历先输出当前节点,再转向右孩子:
ans.emplace_back(root->val); //中序
root= root->right; //中序
后序遍历需要判断:1)没有右孩子或者右孩子被标记输出
2)有右孩子
if(!root->right || root->right == pre) //后序
{
ans.emplace_back(root->val); //后序
pre = root; //后序
root = nullptr; //后序
}
else //后序
{
mystack.emplace(root); //后序
root = root->right; //后序
}
}
return ans;
}
二叉树遍历的变体
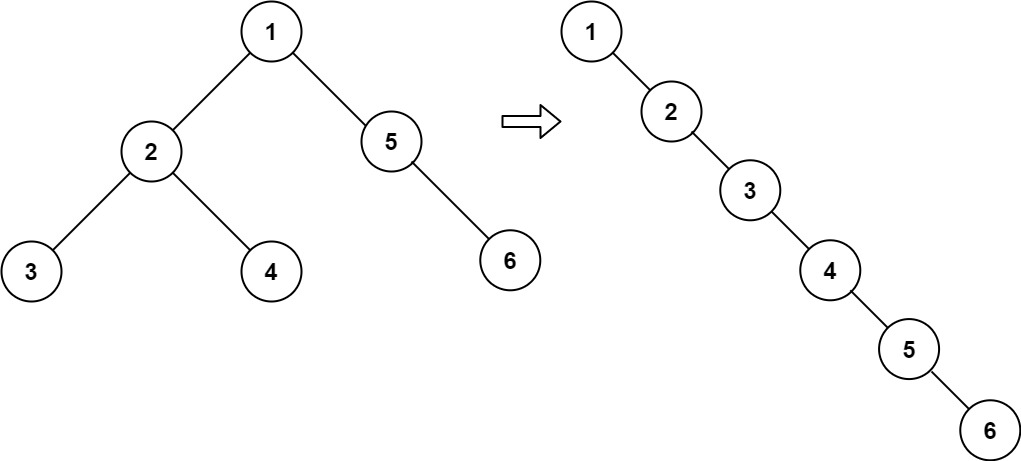
114. 二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:
输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
输入: root = []
输出:[]
【分析】
先前序遍历一遍,将每个节点存入数组,之后更新数组中每个节点的左右子节点的信息,将二叉树展开为单链表。
void flatten(TreeNode* root) {
stack<TreeNode*> mystack;
vector<TreeNode*> myvector;
while(root || !mystack.empty()){
while(root){
myvector.emplace_back(root);
mystack.emplace(root);
root = root->left;
}
root = mystack.top();
mystack.pop();
root = root->right;
}
int n = myvector.size();
for(int i = 1; i < n; ++i){
TreeNode* pre = myvector[i-1];
TreeNode* now = myvector[i];
pre->left = nullptr;
pre->right = now;
}
}
平衡二叉树(AVL)与二叉搜索树
平衡二叉树:
每个节点左右子树高度差的绝对值不能超过1。
二叉搜索树/二叉排序树(BST):
左子树小于根,右子树大于根。
二叉搜索树的中序遍历是升序序列,中序遍历的遍历次序:左子树-根-右子树
平衡二叉搜索树:
满足以上两种树的条件。
删除二叉搜索树的结点:
如果最后要删除的节点左右子树均不为空,寻找右子树中最左节点,用这个最左节点(就是后继节点)替换当前节点,并且将最左节点从原位置删除。
例题:
//LeetCode108. 将有序数组转换为二叉搜索树
//给你一个整数数组 nums,其中元素已经按升序排列,请你将其转换为一棵高度平衡二叉搜索树。
// 总是选择中间位置左边的数字作为根节点
int mid = (left + right) / 2;
// 总是选择中间位置右边的数字作为根节点
int mid = (left + right + 1) / 2;
// 选择任意一个中间位置数字作为根节点
int mid = (left + right + rand() % 2) / 2;
//题解:
TreeNode* sortedArrayToBST(vector<int>& nums)
{
return treeBuild(nums,0,nums.size()-1);
}
TreeNode* treeBuild(vector<int>& nums, int le,int ri)
{
if(le>ri)
{
return nullptr;
}
int mid=(le+ri)/2;
//TreeNode*left,*right;
TreeNode * root = new TreeNode(nums[mid]);
root->left = treeBuild(nums,le,mid-1);
root->right = treeBuild(nums,mid+1,ri);
return root;
}
此题有几点注意:
1)给定二叉搜索树的中序遍历,并要求二叉搜索树的高度平衡,不可以唯一地确定二叉搜索树。
2)在给定中序遍历序列数组的情况下,每一个子树中的数字在数组中一定是连续的,因此可以通过数组下标范围确定子树包含的数字,下标范围记为 [left,right]
3)递归的基准情形是平衡二叉搜索树不包含任何数字,此时平衡二叉搜索树为空。即遍历left=0 到 right=nums.length−1,当 left>right 时,平衡二叉搜索树为空。
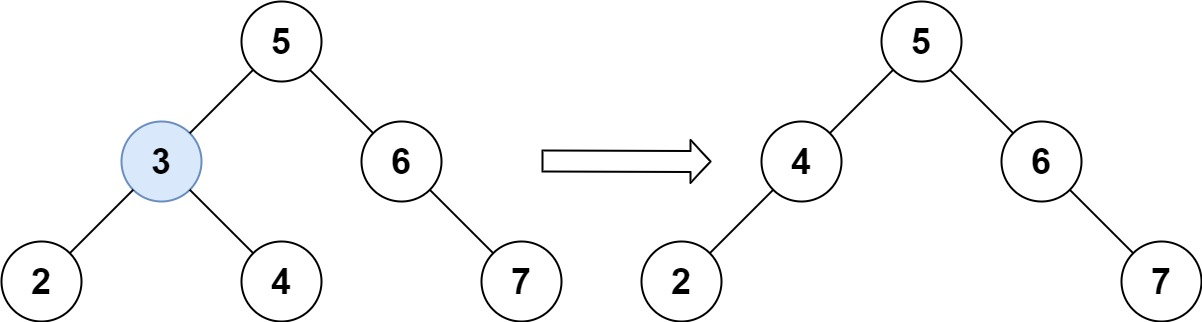
450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。
示例 1:
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。 一个正确的答案是[5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
【分析】二叉搜索树的题目往往可以用递归来解决。进行分类讨论。
TreeNode* deleteNode(TreeNode* root, int key) {
if(!root) return nullptr;
if(key < root->val)
root->left = deleteNode(root->left, key);
else if(key > root->val)
root->right = deleteNode(root->right, key);
else{
if(!root->left && !root->right)
return nullptr;
else if(root->left && !root->right)
return root->left;
//root = root->left;
else if(!root->left && root->right)
//root = root->right; 仅仅改变了root的指向,并没有改变树结构,因为return root,因此这样写也对
return root->right;
else{
auto now = root->right;
while(now->left) now = now->left;
root->val = now->val;
//now = now->right;仅仅是改变了now的指向,并没有改变树结构
///要改变树结构,用now节点的右孩子来代替now节点,需要递归删除now节点
root->right = deleteNode(root->right, now->val);
}
}
return root;
}
N叉树
N叉树结点结构定义:
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};

树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
输入:root = [1,null,3,2,4,null,5,6]
输出:[[1],[3,2,4],[5,6]]
【注意点】按层输出,需要记录每层节点数。此外N叉树比二叉树不同的地方还在于孩子节点数目,每次出队列一个节点时,都需要用for循环来将当前要出队列节点的多个孩子节点入队列。
vector<vector<int>> levelOrder(Node* root) {
vector<vector<int>> ans;
if(!root)
{
return ans;
}
queue<Node*> myque; //Node*
myque.emplace(root);
while(!myque.empty())
{
int n = myque.size();//按层输出,需要记录每层节点数
vector<int> res; //还是这个初始化为n的问题,若res(n),则每次emplace_back都会从前面n个初始0后方添加元素!
for(int i=0; i<n; ++i)
{
Node* node = myque.front();
myque.pop();
res.emplace_back(node->val);
//每个节点都有children数组成员,只是该数组可能不含元素罢了,
//因此不能用node->children[0]这种判断
for(Node* child : node->children)
{
myque.emplace(child);
}
//也可以这样遍历孩子节点
// for(int j=0; j<node->children.size(); ++j)
// myque.emplace(node->children[j]);
}
ans.emplace_back(res);
}
return ans;
}
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
输入:root = [1,null,3,2,4,null,5,6]
输出:[1,3,5,6,2,4]
递归方法:
N 叉树的前序遍历与二叉树的前序遍历的思路和方法基本一致,每次递归时,先访问根节点,然后依次递归访问每个孩子节点即可。
vector<int> ans;
void pre(Node* root)
{
if(!root)
{
return;
}
ans.emplace_back(root->val);
for(Node* child : root->children)
{
pre(child);
}
}
vector<int> preorder(Node* root) {
pre(root);
return ans;
}
非递归方法:
先遍历节点本身,然后从左向右依次先序遍历该每个以子节点为根的子树,此时利用栈先进后出的原理,依次从右向左将子节点入栈,这样出栈的时候即可保证从左向右依次遍历每个子树。
vector<int> preorder(Node* root) {
vector<int> ans;
if(!root)
{
return ans;
}
stack<Node*> mystack;
mystack.emplace(root);
while(!mystack.empty())
{
Node* node = mystack.top();
ans.emplace_back(node->val);
mystack.pop();
for(auto it = node->children.rbegin(); it!= node->children.rend(); ++it)
{
mystack.emplace(*it);
}
}
return ans;
}
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
输入:root = [1,null,3,2,4,null,5,6]
输出:[5,6,3,2,4,1]
非递归方法:
N叉树的后序遍历与前序遍历都是将当前节点的孩子节点从右到左入栈,然后每次取栈顶元素。前序遍历是取到栈顶元素就直接输出,后序遍历相对更复杂一些,需要记录一下当前节点的孩子节点是否都已经入栈,如果没入栈,则不输出当前节点,依次从右到左入栈孩子节点,并将当前节点标记到set中;如果后继孩子都入栈了,才输出当前节点的值,并将栈顶出栈。
后序遍历具体做法:
首先把根节点入栈,因为根节点是前序遍历中的第一个节点。随后每次我们找到栈顶节点 u,如果当前节点的子节点没有遍历过,则应该先把 u 的所有子节点从右向左逆序压入栈中,这样出栈的节点则是顺序从左向右的,同时对节点 u 进行标记,表示该节点的子节点已经全部入栈;如果当前节点 u 为叶子节点或者当前节点的子节点已经全部遍历过,则从栈中弹出节点 u,并记录节点 u的值。例如 u 的子节点从左到右为 v1 ,v2 ,v3 ,那么入栈的顺序应当为 v3,v2,v1,这样就保证了下一个遍历到的节点(即 u 的左侧第一个孩子节点 v1 )出现在栈顶的位置。此时,访问第一个子节点 v1 时,仍然按照此方法则会先访问 v1的左侧第一个孩子节点。
vector<int> postorder(Node* root) {
vector<int> ans;
if(!root)
{
return ans;
}
unordered_set<Node*> myset;//记录成员节点是否已经将孩子都入栈
stack<Node*> mystack;
mystack.emplace(root);
while(!mystack.empty())
{
root = mystack.top();
if(myset.count(root)==0) //1.当前节点的孩子没入栈,需要先从右到左入栈孩子节点
{
for(auto it = root->children.rbegin();it != root->children.rend(); ++it)
{
mystack.emplace(*it);
}
myset.insert(root);//记录已经入栈完孩子节点的当前节点
}
else //2.当前节点的孩子都入栈了,才输出当前节点,并出栈
{
ans.emplace_back(root->val);
mystack.pop();
}
}
return ans;
}
图
图的广度优先搜索类似于树的层次遍历过程。
图的深度优先搜索(Depth First Search),和树的先序遍历比较类似。假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
有向图的入度和出度统计:
vector<int> inDegrees(n + 1);
vector<int> outDegrees(n + 1); //默认初始化都为0
for (auto& edge : trust) {
int x = edge[0], y = edge[1];
......
图的深度优先遍历:
//图的深度优先遍历
//使用深度优先搜索的方式遍历整张图,统计可以到达的节点个数,并利用数组 vis 标记当前节点是否访问过,以防止重复访问。
vector<int> vis;
int num=0;
public:
void DFS(vector<vector<int>>& rooms, int k)
{
vis[k]=1;
num++;
for(int a:rooms[k])
{
if(!vis[a])
{
DFS(rooms,a);
}
}
}
图的层次遍历:
//图的层次遍历
vector<int> vis(n);
vis[0]=1;
queue<int> myque;
myque.push(0);//或者用emplace
while(!myque.empty())
{
int rec=myque.front();//队列是front不是top
myque.pop();
for(int a:rooms[rec])
{
if(!vis[a])
{
vis[a]=1;
num++;
myque.push(a);
}
}
}
拓扑排序
比较好理解的拓扑排序是用广度优先搜索实现。
初始时,所有入度为 0 的节点都被放入队列中,它们就是可以作为拓扑排序最前面的节点,并且它们之间的相对顺序是无关紧要的。
在广度优先搜索的每一步中,我们取出队首的节点 u:
1)我们将 u 放入答案中;
2)我们移除 u 的所有出边,也就是将 u 的所有相邻节点的入度减少 1。如果某个相邻节点 v 的入度变为 0,那么我们就将 v 放入队列中。
在广度优先搜索的过程结束后。如果答案中包含了这 n 个节点,那么我们就找到了一种拓扑排序,否则说明图中存在环,也就不存在拓扑排序了。
207. 课程表
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
【分析】
只需要判断是否存在一种拓扑排序,用一个变量记录被放入答案数组的节点个数。省去存放答案数组,
记录队列中访问过的入度为0的节点数目visted是否等于numCourses,不相等则存在环。
vector<vector<int>> edges;
vector<int> indgree;
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
edges.resize(numCourses);
indgree.resize(numCourses);
for(auto info : prerequisites){
edges[info[1]].emplace_back(info[0]);
indgree[info[0]]++;
}
queue<int> myque;
for(int i = 0; i < numCourses; ++i){
if(indgree[i] == 0){
myque.emplace(i);
}
}
int visted = 0;
while(!myque.empty()){
visted++;
int u = myque.front();
myque.pop();
for(int v : edges[u]){
indgree[v]--;
if(indgree[v] == 0){
myque.emplace(v);
}
}
}
return visted == numCourses;
}
【方法二】利用深度优先搜索实现拓扑排序
思路:遍历邻接表的每行,从该行的每个邻接顶点(下一个指向的节点)开始,进行dfs,若产生环则返回false
实现过程:
在每一轮的搜索搜索开始时,我们任取一个「未搜索」的节点开始进行深度优先搜索。
我们将当前搜索的节点 u 标记为「搜索中」,遍历该节点的每一个相邻节点 v:
1) 如果 v 为「未搜索0」,那么我们开始搜索 v,待搜索完成回溯到 u;
2) 如果 v为「搜索中1」,那么我们就找到了图中的一个环,因此是不存在拓扑排序的;
3)如果 v为「已完成2」,那么说明 v 已经在栈中了,而 u 还不在栈中,因此 u 无论何时入栈都不会影响到(u,v) 之前的拓扑关系,以及不用进行任何操作。
当 u 的所有相邻节点都为「已完成2」时,我们将 u 放入栈中,并将其标记为「已完成2」。
vector<vector<int>> edges;
vector<int> vis;
bool valid = true;//是否存在环,存在环时为false
void dfs(int u){
vis[u] = 1;
for(auto v : edges[u]){
if(vis[v] == 0){
dfs(v);
if(!valid){
return;
}
}else if(vis[v] == 1){
valid = false;
return;
}
}
vis[u] = 2;
}
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
edges.resize(numCourses);
vis.resize(numCourses);
for(auto p : prerequisites){
edges[p[1]].emplace_back(p[0]);
}
for(int i = 0; i < numCourses && valid; ++i){
if (!visited[i]) {
dfs(i);
}
}
return valid;
}
210. 课程表 II
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。
【分析】与上一题的区别就是需要输出拓扑排序的序列
vector<vector<int>> edges;
vector<int> indgree;
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
edges.resize(numCourses);
indgree.resize(numCourses);
for(auto info : prerequisites){
edges[info[1]].emplace_back(info[0]);
indgree[info[0]]++;
}
queue<int> myque;
for(int i = 0; i < numCourses; ++i){
if(indgree[i] == 0){
myque.emplace(i);
}
}
vector<int> ans;
int visted = 0;
while(!myque.empty()){
int u = myque.front();
ans.emplace_back(u);
++visted;
myque.pop();
for(auto v : edges[u]){
--indgree[v];
if(indgree[v] == 0){
myque.emplace(v);
}
}
}
if(visted != numCourses){
return {};
}else{
return ans;
}
}
剑指 Offer II 115. 重建序列
给定一个长度为 n 的整数数组 nums ,其中 nums 是范围为 [1,n] 的整数的排列。还提供了一个 2D 整数数组 sequences ,其中 sequences[i] 是 nums 的子序列。
检查 nums 是否是唯一的最短 超序列 。最短 超序列 是 长度最短 的序列,并且所有序列 sequences[i] 都是它的子序列。对于给定的数组 sequences ,可能存在多个有效的 超序列 。
例如,对于 sequences = [[1,2],[1,3]] ,有两个最短的 超序列 ,[1,2,3] 和 [1,3,2] 。
而对于 sequences = [[1,2],[1,3],[1,2,3]] ,唯一可能的最短 超序列 是 [1,2,3] 。[1,2,3,4] 是可能的超序列,但不是最短的。
如果 nums 是序列的唯一最短 超序列 ,则返回 true ,否则返回 false 。
子序列 是一个可以通过从另一个序列中删除一些元素或不删除任何元素,而不改变其余元素的顺序的序列。
示例 1:
输入:nums = [1,2,3], sequences = [[1,2],[1,3]]
输出:false
解释:有两种可能的超序列:[1,2,3]和[1,3,2]。
序列 [1,2] 是[1,2,3]和[1,3,2]的子序列。
序列 [1,3]是[1,2,3]和[1,3,2]的子序列。
因为 nums 不是唯一最短的超序列,所以返回false。
【分析】拓扑排序
判断根据sequences 中的每个序列构造超序列的结果是否唯一,可以将 sequences 中的所有序列看成有向图,数字 1 到 n 分别表示图中的 n 个结点,每个序列中的相邻数字表示的结点之间存在一条有向边。根据给定的序列构造超序列等价于有向图的拓扑排序。
拓扑排序,需要两个数组分别保存各顶点后继节点和各顶点入度;第三个数组来保存拓扑结果;一个队列保存入度为0的节点;
【细节】
当保存入度为0节点的队列中元素个数大于1时,说明存在不止一种拓扑排序结果。
按理说在将每对序列进行后继和入度记录时,应该先判断一下该对序列有没有被记录过,当然也可以进行重复记录,之后减入度时候也会相应重复减少,不会影响最终结果。
bool sequenceReconstruction(vector<int>& nums, vector<vector<int>>& sequences) {
int n = nums.size();
//注意数组中的数从1开始,不是从0开始,注意数组越界问题。可以存数的时候-1来避免,
//也可将初始size + 1,后面遍历入度时候从下标1开始到n结束即可。
vector<vector<int>> edges(n + 1);
vector<int> indgree(n + 1);
for(auto info : sequences){
int m = info.size();
//sequences中保存的是一个个长度不定的序列,不一定都是两个两个的序列对
//需要将每个序列中的数对拓扑序都找出来,可以检查是否重复,也可不检查
for(int i = 0; i < m - 1; ++i){
edges[info[i]].emplace_back(info[i + 1]);
indgree[info[i + 1]]++;
}
}
vector<int> ans;
queue<int> q;
//注意入队入度为0的顶点时,入的是该顶点的序号,而不是该顶点的入度大小(这样入的永远是0)
for(int i = 1; i <= n; ++i){
if(indgree[i] == 0){
q.emplace(i);
}
}
while(!q.empty()){
if(q.size() > 1){
return false;
}
ans.emplace_back(q.front());
for(int a : edges[q.front()]){
indgree[a]--;
if(indgree[a] == 0){
q.emplace(a);
}
}
q.pop();
}
return nums == ans;
}
如果需要检查是否重复记录了序列对,可以采用哈希集合数组,利用哈希集合的count或者find函数,但亲测这样内存占用更大,运行时间更长。
//如果需要检查是否重复记录了序列对,可以采用哈希集合数组,利用哈希集合的count或者find函数
vector<unordered_set<int>> edges(n + 1);
vector<int> indgree(n + 1);
for(auto info : sequences){
int m = info.size();
//sequences中保存的是一个个长度不定的序列,不一定都是两个两个的数对
//需要将每个序列中的数对拓扑序都找出来
for(int i = 0; i < m - 1; ++i){
//这里利用了count函数
if(edges[info[i]].count(info[i + 1]) == 0){
edges[info[i]].emplace(info[i + 1]);
indgree[info[i + 1]]++;
}
}
}