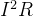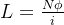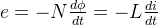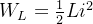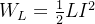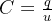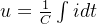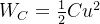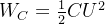电路与电子学复习——电路的基本定律与分析方法 - 悦读

电路与电子学复习——电路的基本定律与分析方法

目录

1.1 电路的基本概念

1.1.1 电路的组成及作用

1.1.2 电流和电压的参考方向

1.1.3功率与能量

1.1.4 电源的工作状态

1.有载工作状态

1.1.5 理想电路元件

理想电压源

理想电流源

恒流源和恒压源同时出现时

理想受控源

1.1.6 电路模型

建模时必须考虑工作条件

1.2 电路的基本定律

1.2.1欧姆定律

1.2.2基尔霍夫定律

1.2.2.1基尔霍夫电流定律（KCL）

1.2.2.2基尔霍夫电压定律（KVL）

1.3 电路的分析方法

1.3.1 支路电流法

1.3.2 节点电压法

1.3.3 电源等效变换法

1.3.4 叠加原理

1.3.5 等效电源定理

1.3.6 电位的计算

1.3.7 含受控源电路的分析

1.1 电路的基本概念

1.1.1 电路的组成及作用

电路的作用：实现电能的传输和转换

电源（信号源）：提供电能（信号）的部分；

负载：吸收或转换电能的部分；

中间环节：连接和控制电源和负载的部分；

1.1.2 电流和电压的参考方向

物理量正方向表示方式：

解题时，先假定“正方向”(即在图中表明物理量的参考方向)，然后再列方程计算。

方程式U/I=R 仅适用于U, I 参考方向一致的情况

为了避免列方程时出错，习惯上把 I 与 U 的方向按相同方向假设，称为关联参考方向。

1.1.3功率与能量

P = U I

负载：若元件上的电压为 U 和电流为 I 的实际方向一致 ,P > 0,则该元件吸收功率,为负载;

电源：若元件上的电压为 U 和电流为 I 的实际方向相反 ,P < 0,则该元件发出功率,为电源。

电路符号为电源在电路中不一定起电源的作用，电路符号为负载在电路中不一定起负载的作用。

需要根据其功率情况来判断在电路中是作为电源还是负载

1.1.4 电源的工作状态

1.有载工作状态

当电源与负载接通，电路中有电流流动，电路的此种状态称为通路，电源的此种状态称为有载状态。

额定值：

对负载：额定值指负载正常工作时的条件及消耗的功率限额。*一般负载必须额定工作!

对电源：额定值指电源向负载提供的电流、电压和功率的限额。*电源使用时不允许超过额定值!

在一定条件下，电源输出的功率取决于负载的大小，所以电源不一定处于额定工作状态，但是一般不应该超过额定值。

Q：电源的额定功率为125kw、220v，接220v、60w的电灯时，电灯会不会烧毁？

A：不会，电源输出的功率为60w

负载一般要额定工作。电源的输出功率取决于负载。

2.电源开路

空载，RL=∞

I = 0； U0 = E； P = 0；

3.电源短路

外电路被短路（RL =0）

I = E / R0； U = 0；P（输出功率） = 0； P（电源消耗） = $I^{2} R$

电源短路容易烧坏电源，因此电源使用中通常接入熔断器

1.1.5 理想电路元件

理想电压源

两端电压可按某种规律变化，而与通过它的电流无关的元件。

特点:

1）输出电压不变，其值恒等于电动势。Uab = E；

2）电源中的电流由外电路决定。

eg：

假设E = 10 V

当R1接入时：I = 10 / 2 = 5 A

I = 10 / ((2 * 2) / (2 + 2)) = 10 A;

理想电流源

通过元件电流可按某种规律变化，而与其两端电压无关的元件。

特点：

1）输出电流不变，其值恒等于电流源电流 Is；

2）输出电压由外电路决定。

eg:

设Is = 10 A

R = 1 Ω 时， U = Is * R = 10 V

R = 2 Ω 时， U = Is * R = 20 V

恒流源和恒压源同时出现时

原则：Is不能变，E 不能变。

恒压源中的电流：I = Is

恒流源两端电压：Uab = - E （注意方向！E的方向与 I 的方向相同，*关联参考方向）

与理想电压源并联的电路（器件），其两端电压等于理想电压源的电压；与理想电流源串联的电路（器件），其电流等于理想电流源的电流。

电阻

由消耗电能的物理过程抽象出来的理想电路元件。

线性电阻： R 恒定不变，伏安特性曲线为直线，表明电阻不变

非线性电阻：R 会改变，伏安特性曲线为曲线，电阻会受温度等因素而改变

电感

由磁能储存的物理过程抽象出来的理想电路元件

线圈是典型的电感元件，忽略其电阻可以认为是一个理想的电感元件。

当电流 I 通过线圈时，线圈中就会有磁通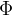 $\Phi$ ，若线圈匝数为N，则线圈的电感定义为单位电流产生的磁链，即 $L = \frac{N\phi }{i}$

电感是表征线圈产生磁通能力的物理量

*电感和结构参数的关系

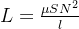
$L = \frac{\mu SN^{2}}{l}$ （ $\mu$ 是磁导率， S是线圈面积， N 是线圈匝数， l 是线圈长度）

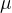
线性电感 : L恒定不变 (如:空心电感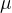 $\mu$ 不变)

非线性电感： L 会改变 (如:铁心电感 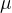$\mu$ 不为常数)

*电感中的感应电动势e

当线圈中的电流发生变化时，它产生的磁通也变化，根据电磁感应定律，在线圈两端将有感应电动势产生。

e的方向：与 I 方向一致

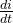
e的大小： $e = -N\frac{d\phi }{dt} = - L\frac{di}{dt}$

在 i 为直流时， $\frac{di}{dt}$ = 0；则 e = 0；

所以,在直流电路中电感相当于短路。可看作导线。

*电感的储能

电感储存的磁场能量为 $W_{L} = \frac{1}{2} Li^{2}$

Q：电感中的电流是直流时, 储存的磁场能量是否为0 ？

A：否， $W_{L} = \frac{1}{2} L I^{2}$

**直流电路中，电感没有感应电动势e，但依旧有储能作用**

电容

由电能储存的物理过程抽象出来的理想电路元件。

**电容是磁能储存，电容是电能储存**

在电容两极板间加电压u，电容即被充电，建立电场。电容定义为单位电压下存储的电荷。

$C=\frac{q}{u}$

*电容和结构参数的关系

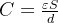
$C=\frac{\varepsilon S}{d}$ ， $\varepsilon$ 是介电常数， S是极板面积， d是极板间距离

线性电容: C恒定不变 ( $\varepsilon$ 不变)

非线性电容： C会改变 ( $\varepsilon$ 不为常数)

*电容上电流、电压的关系

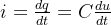
$i = \frac{dq}{dt} = C\frac{du}{dt}$ (q = Cu)

$u = \frac{1}{C}\int idt$

当u = U（直流）时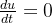， $\frac{du}{dt} = 0$ ，则 i = 0；

所以,在直流电路中电容相当于开路。

*电容的储能

电容储存的电场能量为 $W_{C}=\frac{1}{2}Cu^{2}$

Q：电容两端的电压是直流时, 储存的电场能量是否为0 ？

A：否， $W_{C} = \frac{1}{2}CU^{2}$

Q：电容两端的电压是交流时, 电容储存的磁场能量不为0 ？

A：否，电容无法储存磁场能量

**直流电路中，电容依旧有储能作用**

无源元件汇总

理想受控源

压控电压源：VCVS

流控电压源：VCCS

压控电流源：CCVS

流控电流源：CCCS

受控电压源：方块内线与导线同方向

受控电流源：方块内线与导线垂直

电压控制受控源： U/I = 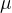$\mu$ （系数） $U_{0}$ （控制电压）

电流控制受控源： U/I = 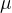$\mu$ （系数） $I_ {0}$ （控制电流）

*独立源和受控源的异同

同：两者性质都属电源，均可向电路提供电压或电流。

异：独立电源的电动势或电流是由非电能量提供的，其大小、方向和电路中的电压、电流无关；受控源的电动势或输出电流，受电路中某个电压或电流的控制。它不能独立存在，其大小、方向由控制量决定。

1.1.6 电路模型

实际元件用理想元件或其组合来近似代替，得到实际电路的模型叫做电路模型。

建模时必须考虑工作条件

直流电路 $\rightarrow$ 电阻元件

低频电路 $\rightarrow$ 电阻元件和电感元件的串联

高频电路 $\rightarrow$ 电阻、电感、电容元件

1.2 电路的基本定律

1.2.1欧姆定律

欧姆定律列方程时，要在图中标明正方向

方向相反时需要添加负号

1.2.2基尔霍夫定律

描述电路中节点上的电流和回路中的电压所满足的普遍规律，其中包括电流和电压两个定律，又称节点电流定律与回路电压定律。

1.支路（Branch）：电路中通过同一电流的每一条分支。

2.节点（Node）：三条或三条以上支路的连接点。

3.回路（Loop）：电路中任一闭合路径。

4.网孔（Mesh）：内部不含有其他支路的回路。

1.2.2.1基尔霍夫电流定律（KCL）

对任何节点，在任一瞬间，流入节点的电流等于由节点流出的电流。

$I_{1} + I_{2} = I_{3}$

（另一表述：在任一瞬间，一个节点上电流的代数和为 0。取流入节点为 “+”，流出节点为“-”。）

$I_{1} + I_2 -I_3 = 0$

**在含有N个节点的电路中，只能列出N-1个独立的KCL方程。**

列KCL的基本步骤

1.找出电路中的节点；

2.指定每一个支路的电流参考方向；

3.对电路节点列写方程: $\sum I_{in} = \sum I_{out}$

KCL的扩展

KCL对包围多个节点的任一闭合面也适用。

eg：

流入： I_A , I_B, I_C

流出：无

故： I_A+I_B+I_C = 0

KCL还适用于电路中任意假设的封闭面，即任一瞬间，通过任意封闭面电流的代数和为0。

eg:

圈出右侧回路，列KCL

I = 0

1.2.2.2基尔霍夫电压定律（KVL）

对电路中的任一回路，沿任意方向绕行一周，各段电压的代数和为 0。即 $\sum U = 0$ 。与绕行方向一致取“＋”，相反取“-”。

l_1 : I_1R_1 + I_3R_3-E_1 = 0

l_2 : I_2R_2 + I_3R_3-E_2 = 0

l_3 : I_1R_1 -I_2R_2+E_2-E_1 = 0

列KVL的基本步骤

1.标出回路中各段电压和电流的参考方向；

2.找出电路中的回路并选定一个绕行方向：顺时针或逆时针；

3.对电路回路列写方程： $\sum U = 0$

KVL的扩展

KVL还适用于电路任一假想回路。

eg1:求 $U_{ab}$

选逆时针为绕行方向，列KVL: $U_1 + U_2+ U_S+U_{ab} = 0$

故： $U_{ab} = -U_1-U_2-U_S$

eg2:求 I_1,I_2,I_3

粉圈（取顺时针） $1\Omega *I_3-3V+4V=0$ $\Rightarrow I_3 = -1A$

红圈（取逆时针） $1\Omega *I_2 +5V - I_3 = 0$ $\Rightarrow I_2 = -6V$

橙圈（KCL） I_1 = I_2+I_3 $\Rightarrow I_1 = -7A$

1.3 电路的分析方法

1.3.1 支路电流法

已知：电路结构和参数

未知：各支路电流

解题思路：根据电路的基本定律，列节点电流和回路电压方程，然后联立求解。

Q:在用基尔霍夫电流定律或电压定律列方程时，可以列出多少个独立的KCL、KVL方程？

A:电路中有N个节点，B 个支路，M 个网孔

独立的KCL方程有（N-1）个 ,独立的KVL方程有（B-N+1）个（一般为网孔个数M）

支路电流法分析电路步骤

1. 选定未知支路电流以及电压或电动势的参考方向；

2. 列独立方程：

电路中有N个节点，B 个支路，M 个网孔

独立的KCL方程有（N-1）个 ,独立的KVL方程有（B-N+1）个（一般为网孔个数M）

3. 解联立方程组，得未知支路电流。

适用范围

适用于支路数较少的电路。

eg：

N=4，B=6，M=3

独立KCL：

a: I_3+I_4-I_1= 0

b: I_1+I_6-I_2= 0

c: I_2-I_5-I_3= 0

独立KVL：

l_1:I_1R_1-I_6R_6+I_4R_4-E_4=0

l_2:I_2R_2+I_5R_5+I_6R_6=0

l_3:I_3R_3-I_4R_4-I_5R_5-E_3+E_4=0

支路中含有恒流源的情况：

当支路中含有恒流源时，若在列KVL方程时，所选回路中不包含恒流源支路，这时，电路中有几条支路含有恒流源，则可少列几个KVL方程。

1.3.2 节点电压法

已知：两节点电路结构和参数

未知：节点电压和支路电流

节点电压：任意选择电路中的某个节点为参考节点，其他节点与此参考节点之间的电压称为节点电压。

对于两节点电路，节点电压计算公式(弥尔曼定理）：

$U_{ab}=\frac{\sum \frac{E_k}{R_k}+\sum I_k}{\sum \frac{1}{R_k}}$

（1）分母各项总为正，等于与该节点相连的各支路的电阻的倒数和。

（2）分子各项的符号：若支路包含电压源，电压源的电压与结点电压一致时为正，反之为负。若该支路包含电流源，电流源的电流流入结点为正，相反为负。

适用范围

适用于分析计算支路数较多，但只含有两个节点的电路。

eg：求 $U_{ab}$

上端为“+”，与流入节点a一致（ $U_{ab}$ 中以a为正，b为负） I_S 流入a节点，取“+”

$U_{ab} = \frac{\frac{E}{R_3} + I_S}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}}$

为什么不是 $\frac{E}{R_2 + R_3}$ ？因为在从a到b的最右端那条回路中，不含有 R_2

**与电流源串联的电阻由于不影响支路电流，不计入分母中。**

eg求 $U_{ab}$

$U=\frac{6+\frac{12}{4}}{\frac{1}{2+2} + \frac{1}{4}} = 18V$

1.3.3 电源等效变换法

1.电压源与电流源的等效变换

等效互换的条件：对外的电压电流相等。（即外特性一致 $I=I^{'},U_{ab}=U_{ab}^{'}$ ）

**注意事项**

（1）“等效”指“对外”等效（等效前后对外伏安特性一致），对内不等效。（消耗能量不同）

（2）注意转换前后 E 与 Is的方向。 Is的方向为原来的E的负极指向正极

（3）恒压源和恒流源不能等效互换（必须要有电阻）

（4）与恒压源串联的电阻和与恒流源并联的电阻可作为其内阻处理。

(5) 串联的恒压源可以合并，并联的恒流源可以合并。（原理：基尔霍夫定律）

2.利用电源的等效变换分析电路

1、所求支路不得参与变换；

2、与恒压源并联的元件、与恒流源串联的元件对外电路不起作用。

易错点：

若使用电源的等效变换

求得 $I=\frac{10-4}{2}=3A$

错因：支路参与了变换；

正解： $I=\frac{10}{2} = 5A$ （电阻两端电压即为恒压源提供的电压，直接用欧姆定律得出结果）

eg：求 I,I_1,U_s ；并判断20V的理想电压源和5A的理想电流源是电源还是负载？

求时，将8 Ω的电阻看作外电路，两个10Ω的电阻对求I 没有影响，可以先将其除去，简化电图。（上方的10Ω电阻能去掉是因为和恒压源并联，下方的10Ω电阻能去掉是因为和恒流源串联）

而后将电流源（5A，2 Ω)等效为电压源（10V，2 Ω)。

$I=\frac{20-10}{8 + 2} = 1A$

求 I_1,U_s 时，因为是内电路，去掉电阻会改变电流、电压。两个10Ω的电阻应保留。

$I_1=I+I_2=1+\frac{20}{10}=3A$

理想电压源的电流方向由‘-’指向‘+’，为电源

U_s = 8I-20-10*5=-62V

理想电流源的电方向由低电位指向高电位，为电源（根据计算结果可知上端为低电位）

1.3.4 叠加原理

在多个电源同时作用的线性电路中，任何支路的电流或任意两点间的电压，都是各个电源单独作用时所得结果的代数和。

线性电路：电路中不含有任何非线性元件

电源单独作用：电路中每次只保留一个电源作用，其余电源均置零。电压源置零指把理想电压源短路，电流源置零指把理想电流源断路，但是要保留各自的内阻。

注意点：

最后将各分电压、分电流叠加时，若总量与分量的参考方向一致则取正，相反则取负。

注意点：

1. 叠加定理只适用于线性电路中电压电流的计算，不能计算功率；

2. 叠加时只将电源分别考虑，电路的结构和参数不变。不作用的恒压源当作短路，即令E=0；不作用的恒流源当作开路，即令 Is=0。

3. 运用叠加定理时也可以把电源分组求解，每个分电路的电源个数可能不止一个。

1.3.5 等效电源定理

二端网络：若一个电路只通过两个输出端与外电路相联，则该电路称为“二端网络”。

无源二端网络：二端网络中不含独立电源

有源二端网络：二端网络中含有独立电源

无源&有源

等效电源定理

有源二端网络用电源模型替代

有源二端网络用电压源模型替代 ------ 戴维宁定理

有源二端网络用电流源模型替代 ------ 诺顿定理

注意点：“等效”是指对端口外等效

戴维宁定理

等效电压源的方向：根据U0的参考方向和代数值确定电压源的极性：U0是正，电压源的方向与U0的参考方向相同，U0为负，电压源的方向与U0的参考方向相反。（等效电压源中理想电压源的方向与开路电压的实际方向相同）

用戴维宁解题步骤：

1.将待求支路画出，其余部分就是一个有源二端网络；

2.求有源二端网络的开路电压；

3.求有源二端网络的等效内阻；

4.画出有源二端网络的等效电路；

5.将1.中画出的支路接入有源二端网络，由此电路计算待求量；

1.3.6 电位的计算

在电路中任选一节点，设其电位为零。此点称为参考点。其它各节点对参考点的电压，便是该节点的电位。记为：“Vx“（注意：电位为单下标，x为节点名称）。

点位与电压的区别

电位值是相对的,参考点选的不同，电路中其它各点的电位也将随之改变；

电路中两点间的电压值是固定的，不会因参考点的不同而改变。

1.3.7 含受控源电路的分析

独立源和受控源的异同

同：两者性质都属电源，均可向电路提供电压或电流。

异：独立电源的电动势或电流是由非电能量提供的，其大小、方向和电路中的电压、电流无关；受控源的电动势或输出电流，受电路中某个电压或电流的控制。它不能独立存在，其大小、方向由控制量决定。

注意点：

1 . 电路的分析方法也适用于受控源电路

2. 用电源的等效变换求解时，含控制量的支路不能参与转换

3. 用叠加原理求解时，受控源一般不单独作用

悦读

道可道，非常道；名可名，非常名。无名，天地之始，有名，万物之母。故常无欲，以观其妙，常有欲，以观其徼。此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

值得收藏的6个OCR文字识别软件，帮你提升10倍工作效率

java程序员能做多久？何时调薪？

最长不下降子序列A1045

GraphRAG： Auto Prompt Tuning 实践

一文搞懂地域和可用区如何选择

银河麒麟桌面系统——桌面鼠标变成x，窗口无关闭按钮的解决办法

Centos7NFS(网络文件系统的搭建)

项目管理工具Maven 概述以及部署过程

aptio设置图解教程2012中文_bios设置图解教程

【Adapter】安卓Android开发中的Activity、Fragment、Adapter

;