树：

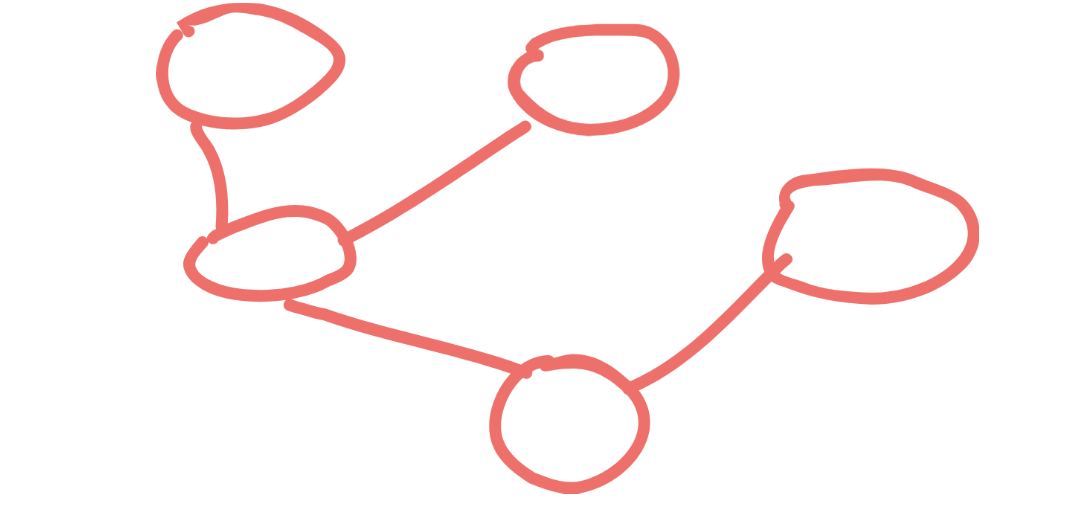
发散性的图，就是树

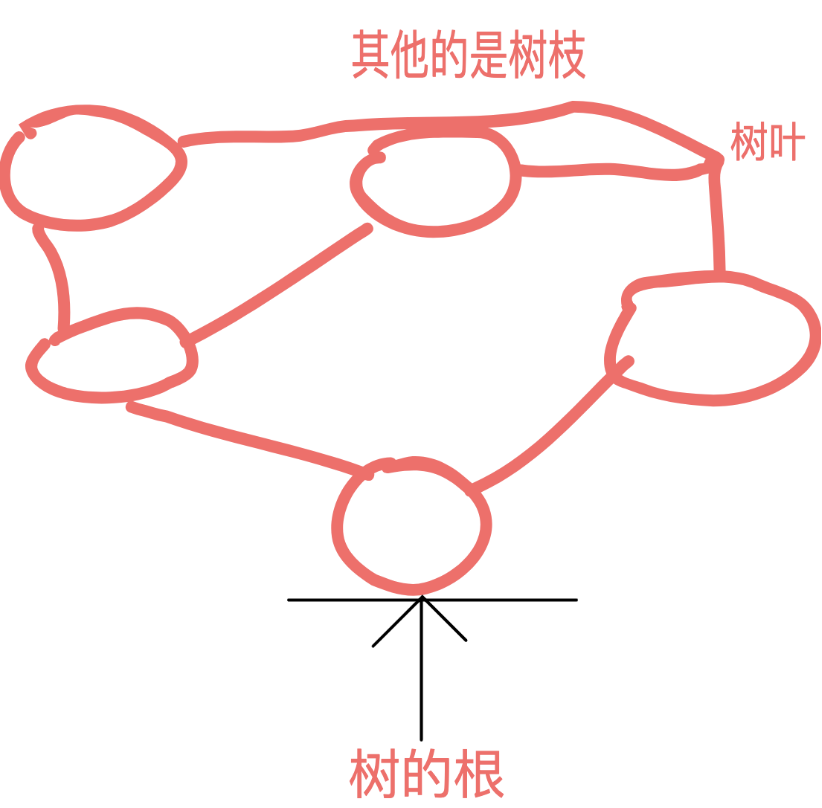
这就是一棵树。

树有n个节点，那么它就有n-1条边。

二叉树：

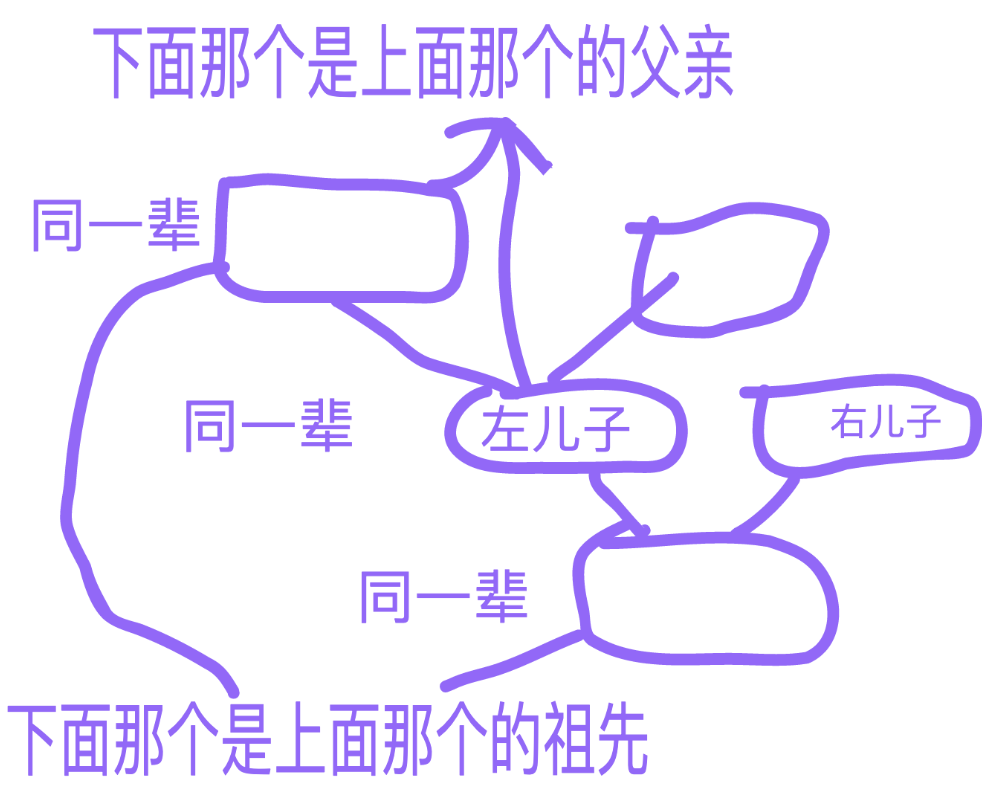
每个节点只指向最多2个节点的数

还是这个，它也是一个二叉树。

结构：

图的存储：

有向图

#include<iostream>

typedef long long Int;

constexpr Int maxN=10;

Int map[1+maxN][1+maxN]{};//map[i][j]==1表示有一条从i号点指向j号点的边

Int n,m;

int main(){

std::cin>>n>>m;

for(Int e=1;e<=m;e++){

Int x,y;

std::cin>>x>>y;

map[x][y]=1;

}

return 0;//map称为邻接矩阵

无向图：

相当于每个有边的节点之间有2条互相指的线段

#include<iostream>

typedef long long Int;

constexpr Int maxN=10;

Int map[1+maxN][1+maxN]{};

Int n,m;

int main(){

std::cin>>n>>m;

for(Int e=1;e<=m;e++){

Int x,y;

std::cin>>x>>y;

map[x][y]=1;

map[y][x]=1;

}

for(Int e=1;e<=n;e++){

for(Int f=1;f<=n;f++){

std::cout<<map[e][f]<<' ';

}

std::cout<<std::endl;

}

return 0;

}

树的表示方法：

有三种：前序遍历，中序遍历，后序遍历。

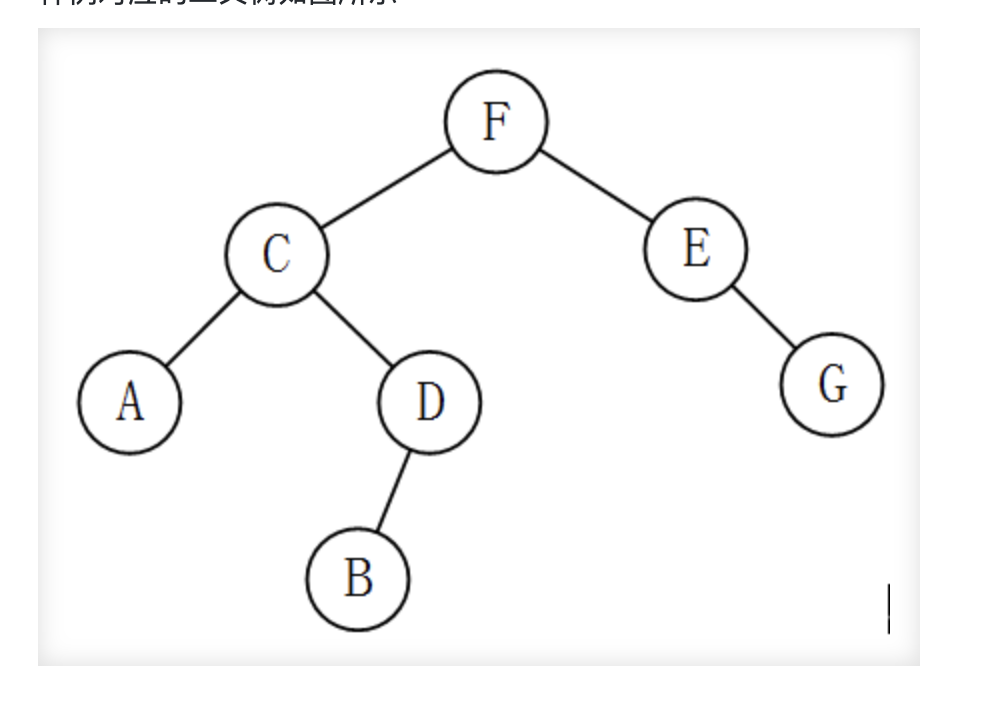
拿这个图示例：

他的前序遍历是FCADBEG

中序遍历是ACBDFEG

后序遍历是：ABDCGEF

前序遍历就是根在前然后从左儿子的树继续，遍历完再遍历右儿子的树

后序遍历就是根在后然后从左儿子的树继续也是一样左儿子在后，遍历完再遍历右儿子的树

中序遍历就是根在中间然后根左边是左儿子的树左儿子在右边一段的中间，遍历完再遍历右儿子的树放右边。