目录
递归的深入讨论与扩展
在前文的基础上,我们将进一步探讨递归的更多细节,包括递归的数学基础、递归与动态规划的关系、递归的空间复杂度分析、递归的替代方案(如迭代和栈模拟递归),以及递归在函数式编程中的应用。通过这些扩展内容,读者将能够更全面地理解递归,并在实际编程中灵活运用。
递归的数学基础
递归与数学归纳法有很强的对应关系。数学归纳法是一种证明方法,用于证明某个命题对所有自然数成立。递归则是将问题分解为更小的子问题,直到达到基准条件。
数学归纳法的步骤:
基准条件:证明命题对最小的自然数(通常是 0 或 1)成立。
归纳假设:假设命题对某个自然数 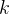
归纳步骤:证明命题对 
递归的对应:
-
基准条件:递归的终止条件。
-
递归条件:将问题分解为更小的子问题。
示例:斐波那契数列
数学归纳法:证明 对所有
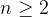
递归实现:直接对应数学公式。
递归与动态规划的关系
动态规划(Dynamic Programming, DP)是一种通过存储子问题的解来避免重复计算的优化技术。递归是动态规划的基础,许多动态规划问题可以通过递归的方式描述。
示例:斐波那契数列的动态规划实现(Python)
def fibonacci(n):
if n <= 1:
return n
dp = [0] * (n + 1)
dp[0], dp[1] = 0, 1
for i in range(2, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]
n = 50
print(f"Fibonacci of {n} is {fibonacci(n)}")递归的空间复杂度分析
递归的空间复杂度主要由递归调用栈的深度决定。每次递归调用都会占用一定的栈空间,因此递归深度过大会导致栈溢出。
示例:阶乘递归的空间复杂度
递归深度:
空间复杂度:
优化方法:
尾递归优化:某些编译器或解释器会对尾递归进行优化,将其转换为迭代,从而减少栈空间的使用。
迭代替代:将递归改写为迭代,使用循环和变量代替递归调用。
递归的替代方案
1. 迭代
迭代是递归的常见替代方案,通常通过循环实现。迭代的空间复杂度较低,且不会出现栈溢出问题。
示例:斐波那契数列的迭代实现(Python)
def fibonacci(n):
if n <= 1:
return n
a, b = 0, 1
for _ in range(2, n + 1):
a, b = b, a + b
return b
n = 50
print(f"Fibonacci of {n} is {fibonacci(n)}")2. 栈模拟递归
对于非尾递归的情况,可以使用显式的栈数据结构来模拟递归调用。
示例:二叉树的中序遍历(栈模拟递归,Python)
def inorder_traversal(root):
stack, result = [], []
current = root
while current or stack:
while current:
stack.append(current)
current = current.left
current = stack.pop()
result.append(current.val)
current = current.right
return result
递归在函数式编程中的应用
函数式编程语言(如 Haskell、Lisp、Scala)天然支持递归,并且通常会对尾递归进行优化。递归在函数式编程中常用于以下场景:
-
列表操作:如 map、filter、reduce 等。
-
树和图的遍历:如递归处理嵌套数据结构。
-
惰性计算:通过递归实现无限序列。
示例:Haskell 中的递归实现阶乘
factorial :: Integer -> Integer
factorial 0 = 1 -- 基准条件
factorial n = n * factorial (n - 1) -- 递归条件递归的更多应用场景
分形图形生成:如绘制科赫雪花、谢尔宾斯基三角形等。
语法解析:如解析数学表达式、JSON 数据等。
组合优化问题:如旅行商问题、背包问题等。
总结
递归是一种强大的编程工具,能够将复杂问题分解为简单的子问题,使代码更加简洁和优雅。然而,递归也有其局限性,如栈溢出和效率问题。通过记忆化、尾递归优化、动态规划等技术,可以有效提升递归的性能。同时,递归与迭代各有优缺点,应根据具体问题选择合适的方法。
掌握递归需要大量的练习和实践。希望本文的内容能够帮助读者深入理解递归,并在实际编程中灵活运用。递归不仅是编程技巧,更是一种思维方式,能够帮助我们更好地理解和解决复杂问题。通过不断学习和实践,读者将能够在算法设计、数据结构、函数式编程等领域中游刃有余地使用递归。
人工智能:如决策树、博弈树搜索等。