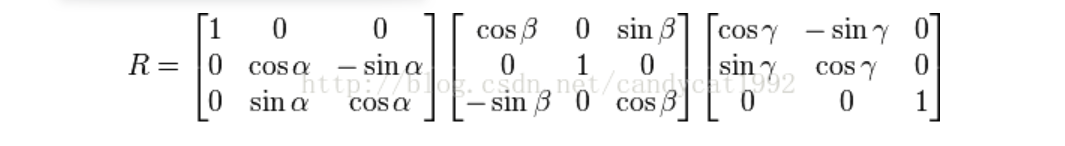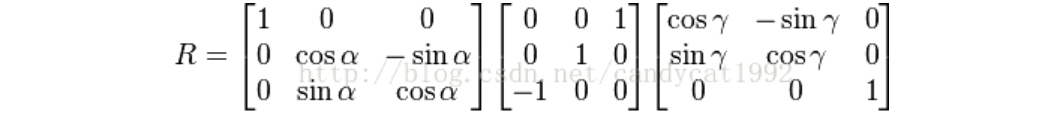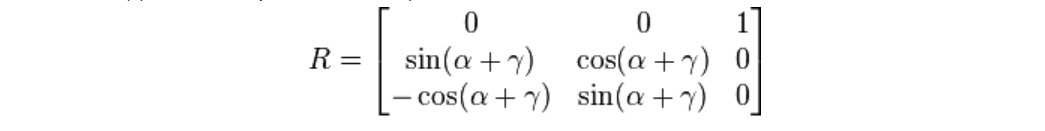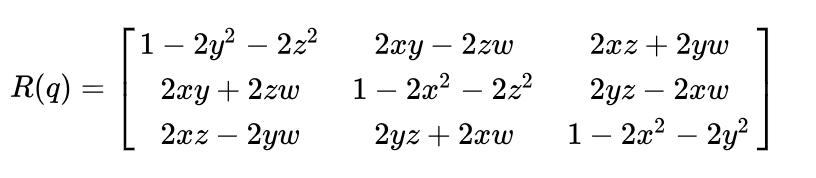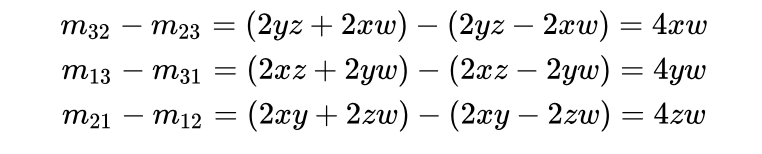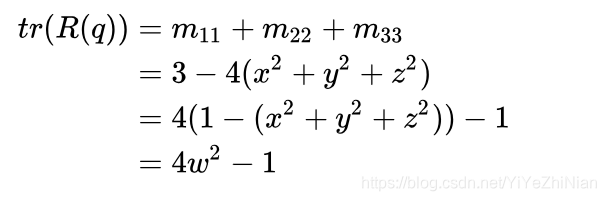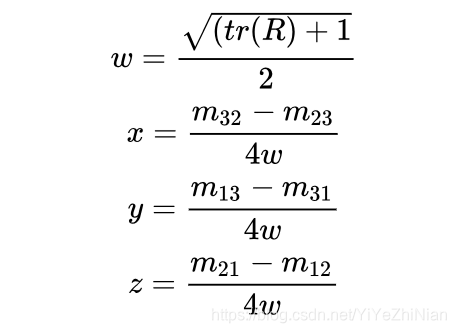1、欧拉角

欧拉角使用最简单的x,y,z值来分别表示在x，y，z轴上的旋转角度，其取值为0-360(或者0-2pi），一般使用roll，pitch，yaw来表示这些分量的旋转值。需要注意的是，这里的旋转是针对世界坐标系说的，这意味着第一次的旋转不会影响第二、三次的转轴。

欧拉旋转
欧拉旋转的数学实现就是使用矩阵。而最常见的表示方法就是3*3的矩阵。在Wiki里我们可以找到这种矩阵的表示形式，以下以按XYZ的旋转顺序为例，三个矩阵分别表示了：

万向节锁
虽然欧拉旋转非常容易理解，但它会造成臭名昭著的万向节锁问题。从最简单的矩阵来理解。还是使用XYZ的旋转顺序。当Y轴的旋转角度为90°时，我们会得到下面的旋转矩阵：

我们对上述矩阵进行左乘可以得到下面的结果：

可以发现，此时当我们改变第一次和第三次的旋转角度时，是同样的效果，而不会改变第一行和第三列的任何数值，从而缺失了一个维度。
Wiki上写，万向节锁出现的本质原因，是因为从欧拉角到旋转的映射并不是一个覆盖映射，即它并不是在每个点处都是局部同胚的。通俗一下解释，这意味着，从欧拉角到旋转是一个多对一的映射（即不同的欧拉角可以表示同一个旋转方向），而且并不是每一个旋转变化都可以用欧拉角来表示。其他更多的大家去参考wiki吧。

所以欧拉角容易出现的问题是 ：
1）不易在任意方向的旋转轴插值；
2）万向节死锁；
3）旋转的次序无法确定。

2、轴角

轴角用一个以单位矢量定义的旋转角，再加上一个标量定义的旋转角来表示旋转。通常的表示[x,y,z,theta]，前面三个表示轴，最后一个表示角度。表示非常直观，也很紧凑。

轴角最大的一个局限就是不能进行简单的插值，此外，轴角形式的旋转不能直接施于点或矢量，必转换为矩阵或者四元数。

3、四元数

四元数（Quaternions）是由爱尔兰数学家哈密顿(William Rowan Hamilton,1805-1865）在1843年发明的数学概念。四元数的乘法不符合交换律（commutative law）。

明确地说，四元数是复数的不可交换延伸。如把四元数的集合考虑成多维实数空间的话，四元数就代表着一个四维空间，相对于复数为二维空间。

四元数的基本性质：
四元数就是形如 ai+bj+ck+d 的数，a、b、c、d是实数。
i^2=j2=k^2=-1
ij=k、ji=-k、jk=i、kj=-i、ki=j、ik=-j

四元数的乘法定义如下，利用简单的分配律就是了：
q1 * q2 =
(w1w2 - x1x2 - y1y2 - z1z2) +
(w1x2 + x1w2 + y1z2 - z1y2) i +
(w1y2 - x1z2 + y1w2 + z1x2) j +
(w1z2 + x1y2 - y1x2 + z1w2) k

由于q = w + x i + y j + z k中可以分为纯量w与向量x i + y j + z k，所以为了方便表示，将q表示为(S, V)，其中S表示纯量w，V表示向量x i + y j + z k，所以四元数乘法又可以表示为：
q1 * q2 = (S1 + V1)(S2 + V2) = S1S2 - V1.V2 + V1XV2 + S1V2 + S2V1

求模：
N(q) = √(x^2 + y^2 + z^2 +w^2)

求共轭：
q*=(w,-x, -y, -z)

求逆：
对于向量逆的定义, q-1 =q*/|q|2
对于单位四元素，分母为1，q-1 =q*=(w,-x, -y, -z)

4、四元数与空间旋转

四元素与轴角的表示很接近，也是使用一个3维向量表示转轴和一个角度分量表示绕此转轴的旋转角度，即(w,x,y,z)， 其中:

w = cos(theta/2)
x = ax * sin(theta/2)
y = ay * sin(theta/2)
z = az * sin(theta/2)
四元数对于空间旋转的计算通过一个向量左乘四元数再右乘该四元数的逆得到：
v‘ = qvq-1
例如我有一个向量v(1，0，1),旋转轴p为（0，1，0）,我希望v绕着p顺时针旋转180°（注意：在四元数空间中使用右手定则表示旋转方向，也就是逆时针）。
根据上面的式子我们可以得到：

q=（0，0，1，0）；
q’=（0，0，-1，0）；
将向量改写成四元数的形式：
v=（0，1，0，1）
注：这里令向量的“w”为“0”。
通过四元数的表示方法：

q=j;
q’=-j;
v=i+k;
则v’=qvq’=j(i+k)(-j)
=(ji+jk)(-j)
=(-k+i)(-j)
=kj-ij
=-i-k
写成向量的形式：
v’=(-1，0，-1）
与我们直观上的理解是一样的，只是它通过一个简单的运算能够更快速的算出这个结果。虽然这里举的例子很简单，但是对于更一般的情况下计算方式也是一样的，只是在思维上没有这么直观。

总结一下：感觉四元数与轴角其实很相似，但是表达的方式不一样，轴角无法进行插值运算，但是四元数可以。嗯。。。不是很能理解。另外计算上面似乎四元数也更简单一点。
学习的时候找到了几篇还不错的文章，如果有想深入理解的可以参考一下，非常详细：

5、四元数(Quaternion)与旋转矩阵

5.1 四元数到旋转矩阵

欧拉旋转是有万向节死锁(Gimbal Lock)的问题的。幸好我们有四元数(Quaternion)这种数学工具可以避免这个情况。一般来说，我们都会用单位四元数 来表示旋转，那么给定一个单位四元数，可以构造旋转矩阵(column major）：
这里的过程参考于：

1、Henderson, D.M… Euler angles, quaternions, and transformation matrices for space shuttle analysis[C]//NASA, Jun 09, 1977.
2、https://en.wikipedia.org/wiki/Rotation_matrix
3、Tomas K.M. , Eric H., Naty H… Real Time Rendering 3rd Edition , p76-p77, 2008.
4、http://run.usc.edu/cs520-s12/quaternions/quaternions-cs520.pdf

这个四元数构造的大概思路就是把四元数的旋转操作写成矩阵形式。

5.2 旋转矩阵到四元数

要从旋转矩阵里提取四元数，也是可以像提取欧拉角那样，用参数化过的矩阵的表达式凑出来。参考《Real Time Rendering 3rd edition》Chapter4的思路，我们观察一下用四元数分量进行参数化的矩阵 ，然后经过一顿操作，我们发现：

于是我们再凑出个实分量w ，就可以把四元数四个分量都用矩阵元素表示出来了。于是我们又机智地发现了一个等式：

其中tr®是矩阵 R 的迹(trace)，也就是矩阵对角元素的和。因为这里用的是3x3矩阵，跟其他资料里面的表示有一点不同。所以我们可以把四元数的四个分量都用矩阵元素凑出来了：

https://krasjet.github.io/quaternion/quaternion.pdf

https://blog.csdn.net/weixin_38294178/article/details/87872893?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-3.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-3.nonecase

https://blog.csdn.net/weixin_34367257/article/details/93387530?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase

https://www.qiujiawei.com/understanding-quaternions/