为什么要做 LeetCode Top 100 题

前言介绍

LeetCode Top 100 经典题目是算法与编程领域内公认的一系列具有挑战性和代表性的问题，它们之所以经典和受欢迎，主要有以下几个原因：

1. 基础性：这些题目覆盖了算法和数据结构的各个方面，如数组、链表、树、图、动态规划、贪心算法等，是学习和巩固编程基础不可或缺的部分。
2. 代表性：这些问题往往代表了某一类算法问题的解题思路和方法，解决它们可以帮助理解更广泛的算法问题。
3. 实战性：许多题目来源于真实世界的工程问题，解决这些题目能够提高解决实际问题的能力。
4. 挑战性：这些题目通常需要深入的思考和巧妙的设计，解决它们能够带来成就感和满足感。
5. 面试相关性：在技术公司的面试中，LeetCode 题目经常被用作考察求职者编程和算法能力的工具，因此受到广泛重视。

以下是部分经典题目的介绍：

1.1 数据结构相关

• 两数之和（Two Sum）：考察哈希表的运用，如何快速查找元素。
• 合并两个有序链表（Merge Two Sorted Lists）：练习链表操作的基本技巧。
• 有效的括号（Valid Parentheses）：栈的经典应用，用于匹配括号序列。

1.2 动态规划

• 最长公共子序列（Longest Common Subsequence）：DP入门问题，处理序列相关问题。
• 打家劫舍（House Robber）：考察动态规划的状态转移和空间优化。
• 买卖股票的最佳时机（Best Time to Buy and Sell Stock）：一系列问题，通过动态规划解决金融类问题。

1.3 树

• 二叉树的遍历（Binary Tree Inorder/Preorder/Postorder Traversal）：理解树的递归和非递归遍历。
• 二叉树的层次遍历（Binary Tree Level Order Traversal）：队列在树中的应用。

1.4 图

• 岛屿数量（Number of Islands）：使用深度优先搜索（DFS）或广度优先搜索（BFS）解决图问题。

1.5 贪心算法

• 跳跃游戏（Jump Game）：通过局部最优解达到全局最优解。

1.6 字符串

• 最长回文子串（Longest Palindromic Substring）：动态规划和中心扩展法的应用。

1.7 其他

• 合并K个排序链表（Merge k Sorted Lists）：优先队列和分治算法的应用。
• 寻找旋转排序数组中的最小值（Find Minimum in Rotated Sorted Array）：二分查找的高级应用。

这些题目因为它们在面试中的高频出现，以及它们在算法学习中的基础和核心地位，而成为经典。它们帮助程序员不仅提升编程技能，还能在面试中更好地展示自己的逻辑思维和问题解决能力。

2. 正文开始

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

提示：

• 2 <= nums.length <= 104
• -109 <= nums[i] <= 109
• -109 <= target <= 109
• 只会存在一个有效答案

python 参考题解：

第一道题是 "Two Sum"，题目描述如下： 给定一个整数数组 `nums` 和一个目标值 `target`，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。 你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素。

示例:

给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

以下是用 Python 给出的题解：

def twoSum(nums, target):
    # 创建一个字典用于存储已经遍历过的数字及其索引
    num_dict = {}
    
    # 遍历数组中的每一个元素及其索引
    for i, num in enumerate(nums):
        # 计算当前元素与目标值的差值
        complement = target - num
        
        # 如果差值在字典中，说明找到了一对和为target的数字
        if complement in num_dict:
            # 返回这对数字的索引
            return [num_dict[complement], i]
        
        # 将当前元素及其索引存入字典
        num_dict[num] = i
    
    # 如果没有找到，返回空列表
    return []
# 示例
nums = [2, 7, 11, 15]
target = 9
print(twoSum(nums, target))  # 输出: [0, 1]

解题思路和步骤：

1. 初始化字典：首先，我们创建一个空字典 num_dict，用于存储遍历过的数字及其索引。
2. 遍历数组：使用 enumerate 函数遍历数组 nums，这样可以同时获得元素值 num 和它的索引 i。
3. 计算差值：对于数组中的每一个元素，我们计算它与目标值 target 的差值 complement。
4. 查找差值：检查这个差值是否已经在字典 num_dict 中。如果在，说明我们找到了一对和为 target 的数字，因为当前的数字加上字典中存储的数字（它们的索引）就是目标值。
5. 返回结果：如果差值在字典中，我们返回差值的索引和当前元素的索引。
6. 更新字典：如果差值不在字典中，我们将当前元素的值和它的索引存入字典，以便后续查找。
7. 结束遍历：如果遍历完整个数组都没有找到结果，则返回空列表。根据题目描述，这种情况不会发生。
   这个算法的时间复杂度是 O(n)，因为每个元素最多被遍历一次。空间复杂度也是 O(n)，因为我们需要存储遍历过的元素及其索引。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

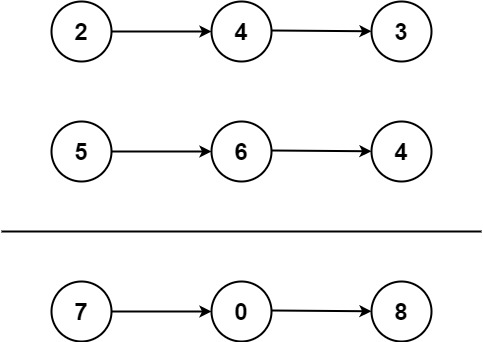
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

提示：

• 每个链表中的节点数在范围 [1, 100] 内
• 0 <= Node.val <= 9
• 题目数据保证列表表示的数字不含前导零

python 参考题解：

第二道题是 "Add Two Numbers"，题目描述如下： 给定两个非空链表来表示两个非负整数。位数按照逆序方式存储，它们的每个节点只存储单个数字。将两数相加返回一个新的链表。 你可以假设除了数字 0 之外，这两个数字都不会以零开头。

示例:

输入: (2 -> 4 -> 3) + (5 -> 6 -> 4)
输出: 7 -> 0 -> 8
解释: 342 + 465 = 807.

以下是用 Python 给出的题解：

# 定义链表节点
class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None
def addTwoNumbers(l1, l2):
    # 初始化哑节点和当前节点
    dummy = ListNode(0)
    current = dummy
    carry = 0
    # 遍历两个链表，直到两个链表都为空
    while l1 or l2:
        # 获取两个链表的当前值，如果链表为空，则值为0
        x = l1.val if l1 else 0
        y = l2.val if l2 else 0
        
        # 计算当前位的和以及进位
        sum_val = x + y + carry
        carry = sum_val // 10
        
        # 将当前和的个位数添加到新链表中
        current.next = ListNode(sum_val % 10)
        current = current.next
        
        # 移动链表指针
        if l1:
            l1 = l1.next
        if l2:
            l2 = l2.next
    # 如果最后有进位，添加一个新节点
    if carry > 0:
        current.next = ListNode(carry)
    # 返回哑节点的下一个节点，即新链表的头节点
    return dummy.next
# 示例
# 创建链表 2 -> 4 -> 3
l1 = ListNode(2)
l1.next = ListNode(4)
l1.next.next = ListNode(3)
# 创建链表 5 -> 6 -> 4
l2 = ListNode(5)
l2.next = ListNode(6)
l2.next.next = ListNode(4)
# 调用函数并打印结果
result = addTwoNumbers(l1, l2)
while result:
    print(result.val, end=" -> ")
    result = result.next
# 输出: 7 -> 0 -> 8

解题思路和步骤：

1. 初始化哑节点：创建一个哑节点（dummy node）用于简化边界条件的处理，哑节点的下一个节点将是返回的新链表的头节点。
2. 初始化进位变量：创建一个变量 carry 用于存储两数相加的进位。
3. 遍历链表：使用一个循环来遍历两个链表，直到两个链表都为空。在循环中，我们处理每个节点的值。
4. 处理节点值：获取两个链表的当前节点值，如果链表为空，则值为0。
5. 计算和及进位：将两个节点的值加上前一次计算的进位 carry，计算新的和 sum_val 以及新的进位 carry。
6. 创建新节点：将 sum_val 的个位数（sum_val % 10）作为新链表的当前节点值，并将新节点链接到当前节点的 next。
7. 移动指针：将当前节点指针移动到下一个节点，并更新两个输入链表的指针。
8. 处理最后的进位：如果循环结束后，carry 大于0，则需要在链表末尾添加一个新的节点。
9. 返回结果：返回哑节点的下一个节点，即新链表的头节点。
   这个算法的时间复杂度是 O(max(m, n))，其中 m 和 n 分别是两个链表的长度，因为我们最多遍历两个链表各一次。空间复杂度是 O(max(m, n))，因为我们需要存储结果链表的节点。

示例 1:

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: s = "pwwkew"
输出: 3

解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
请注意，你的答案必须是 子串 的长度，"pwke" 是一个 子序列，不是子串。

提示：

• 0 <= s.length <= 5 * 104
• s 由英文字母、数字、符号和空格组成

python 参考题解：

第三道题是 "Longest Substring Without Repeating Characters"，题目描述如下： 给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

以下是用 Python 给出的题解：

def lengthOfLongestSubstring(s):
    # 初始化最长子串长度为0，左边界为-1
    max_len = 0
    left = -1
    # 使用字典来存储字符及其在字符串中的索引
    char_map = {}
    
    # 遍历字符串中的每一个字符
    for i, char in enumerate(s):
        # 如果字符在字典中，且其索引大于左边界，更新左边界
        if char in char_map and char_map[char] > left:
            left = char_map[char]
        # 更新最长子串长度
        max_len = max(max_len, i - left)
        # 更新字符在字典中的索引
        char_map[char] = i
    return max_len
# 示例
print(lengthOfLongestSubstring("abcabcbb"))  # 输出: 3
print(lengthOfLongestSubstring("bbbbb"))     # 输出: 1

解题思路和步骤：

1. 初始化变量：首先，我们初始化最长子串长度 max_len 为0，左边界 left 为-1。我们还需要一个字典 char_map 来存储字符及其在字符串中的索引。
2. 遍历字符串：使用 enumerate 函数遍历字符串中的每一个字符及其索引。
3. 检查字符是否重复：对于每一个字符，检查它是否已经在字典 char_map 中，并且它的索引是否大于当前的左边界 left。如果条件成立，说明我们找到了一个重复的字符，需要更新左边界 left 为该字符的索引。
4. 更新最长子串长度：计算当前不重复子串的长度（即当前索引 i 减去左边界 left），并与 max_len 比较，取较大值更新 max_len。
5. 更新字符索引：在字典 char_map 中更新当前字符的最新索引。
6. 返回结果：遍历完成后，返回 max_len 作为结果。
   这个算法的时间复杂度是 O(n)，其中 n 是字符串的长度，因为我们只需要遍历字符串一次。空间复杂度是 O(min(m, n))，其中 m 是字符集的大小（例如，ASCII字符集大小为128），因为我们需要存储字符及其索引，而在最坏的情况下，字符集的大小决定了字典的大小。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

提示：

• nums1.length == m
• nums2.length == n
• 0 <= m <= 1000
• 0 <= n <= 1000
• 1 <= m + n <= 2000
• -106 <= nums1[i], nums2[i] <= 106

python 参考题解：

第四道题是 "Median of Two Sorted Arrays"，题目描述如下： 给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。 请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。 你可以假设 nums1 和 nums2 不会同时为空。

示例 1:

nums1 = [1, 3]
nums2 = [2]
则中位数是 2.0

示例 2:

nums1 = [1, 2]
nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5

以下是用 Python 给出的题解：

def findMedianSortedArrays(nums1, nums2):
    # 确保 nums1 是较短的数组
    if len(nums1) > len(nums2):
        nums1, nums2 = nums2, nums1
    m, n = len(nums1), len(nums2)
    imin, imax, half_len = 0, m, (m + n + 1) // 2
    while imin <= imax:
        i = (imin + imax) // 2
        j = half_len - i
        if i < m and nums1[i] < nums2[j - 1]:
            # i 需要增大
            imin = i + 1
        elif i > 0 and nums1[i - 1] > nums2[j]:
            # i 需要减小
            imax = i - 1
        else:
            # i 正确
            if i == 0: max_of_left = nums2[j - 1]
            elif j == 0: max_of_left = nums1[i - 1]
            else: max_of_left = max(nums1[i - 1], nums2[j - 1])
            if (m + n) % 2 == 1:
                return max_of_left
            if i == m: min_of_right = nums2[j]
            elif j == n: min_of_right = nums1[i]
            else: min_of_right = min(nums1[i], nums2[j])
            return (max_of_left + min_of_right) / 2.0
# 示例
print(findMedianSortedArrays([1, 3], [2]))  # 输出: 2.0
print(findMedianSortedArrays([1, 2], [3, 4]))  # 输出: 2.5

解题思路和步骤：

1. 确保nums1较短：首先，我们确保 nums1 是两个数组中较短的一个，这样可以减少搜索的范围。
2. 初始化变量：定义变量 m 和 n 分别表示 nums1 和 nums2 的长度，imin 和 imax 分别表示在 nums1 中搜索的起始和结束位置，half_len 表示合并后数组中位数的索引位置。
3. 二分搜索：在 nums1 中使用二分搜索找到正确的分割位置 i。对于 nums1 中的每个位置 i，我们计算 nums2 中的位置 j，使得 i + j = half_len。
4. 调整搜索范围：如果 nums1[i] 小于 nums2[j - 1]，则意味着 i 太小，需要增大 i；如果 nums1[i - 1] 大于 nums2[j]，则意味着 i 太大，需要减小 i。
5. 找到正确的分割位置：当找到正确的分割位置时，我们计算合并后数组左侧的最大值 max_of_left 和右侧的最小值 min_of_right。
6. 计算中位数：如果合并后数组的长度是奇数，则中位数是 max_of_left；如果是偶数，则中位数是 (max_of_left + min_of_right) / 2.0。
7. 返回结果：返回计算出的中位数。
   这个算法的时间复杂度是 O(log(min(m, n)))，因为我们在较短的数组上使用了二分搜索。空间复杂度是 O(1)，因为我们没有使用额外的空间来存储合并后的数组。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

提示：

• 1 <= s.length <= 1000
• s 仅由数字和英文字母组成

python 参考题解：

第五道题是 "Longest Palindromic Substring"，题目描述如下： 给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。 示例 1:

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

示例 2:

输入: "cbbd"
输出: "bb"

以下是用 Python 给出的题解：

def longestPalindrome(s):
    # 如果字符串为空或长度为1，直接返回原字符串
    if len(s) < 2:
        return s
    
    # 初始化最长回文子串的起始和结束位置
    start, end = 0, 0
    
    # 遍历字符串的每一个字符
    for i in range(len(s)):
        # 分别检查以当前字符为中心的奇数长度和偶数长度的回文子串
        len1 = expandAroundCenter(s, i, i)
        len2 = expandAroundCenter(s, i, i + 1)
        # 取两者中的最大长度
        max_len = max(len1, len2)
        
        # 如果找到更长的回文子串，更新起始和结束位置
        if max_len > end - start:
            start = i - (max_len - 1) // 2
            end = i + max_len // 2
    
    # 返回最长回文子串
    return s[start:end+1]
def expandAroundCenter(s, left, right):
    # 当左右指针没有越界且字符相等时，继续向外扩展
    while left >= 0 and right < len(s) and s[left] == s[right]:
        left -= 1
        right += 1
    # 返回以s[left]和s[right]为中心的回文子串长度
    return right - left - 1
# 示例
print(longestPalindrome("babad"))  # 输出: "bab" 或 "aba"
print(longestPalindrome("cbbd"))   # 输出: "bb"

解题思路和步骤：

1. 边界情况处理：首先，如果字符串为空或长度为1，则直接返回原字符串，因为单个字符或空字符串都是回文串。
2. 初始化变量：定义变量 start 和 end 来记录最长回文子串的起始和结束位置。
3. 遍历字符串：使用一个循环遍历字符串的每一个字符。
4. 检查回文子串：对于每个字符，我们检查以该字符为中心的奇数长度和偶数长度的回文子串。这是通过 expandAroundCenter 函数完成的。
5. 扩展中心：在 expandAroundCenter 函数中，我们使用两个指针分别向左和向右扩展，直到它们指向的字符不相等或指针越界。
6. 更新最长回文子串：比较当前找到的回文子串长度和之前记录的最长长度，如果当前长度更长，则更新 start 和 end。
7. 返回结果：最后，根据 start 和 end 的位置返回最长回文子串。
   这个算法的时间复杂度是 O(n^2)，其中 n 是字符串的长度，因为我们对于每个字符都要进行一次扩展操作，最坏情况下需要遍历整个字符串。空间复杂度是 O(1)，因为我们只使用了常数级别的额外空间。