知识点

基本流程

1. 确定基本流程和假设，确认做这个功能是为了提升/降低什么指标。
2. 开发相关功能
3. 设计分层实验，进行流量分配。通过PowerAnalysis计算最小样本量。
4. 实验达到最小样本量后，进行SRM检验，检验分流是否符合预期，若不符合预期，则回去检查分流系统正确性。
5. 若通过SRM检验，进行效果分析，得出实验结论。

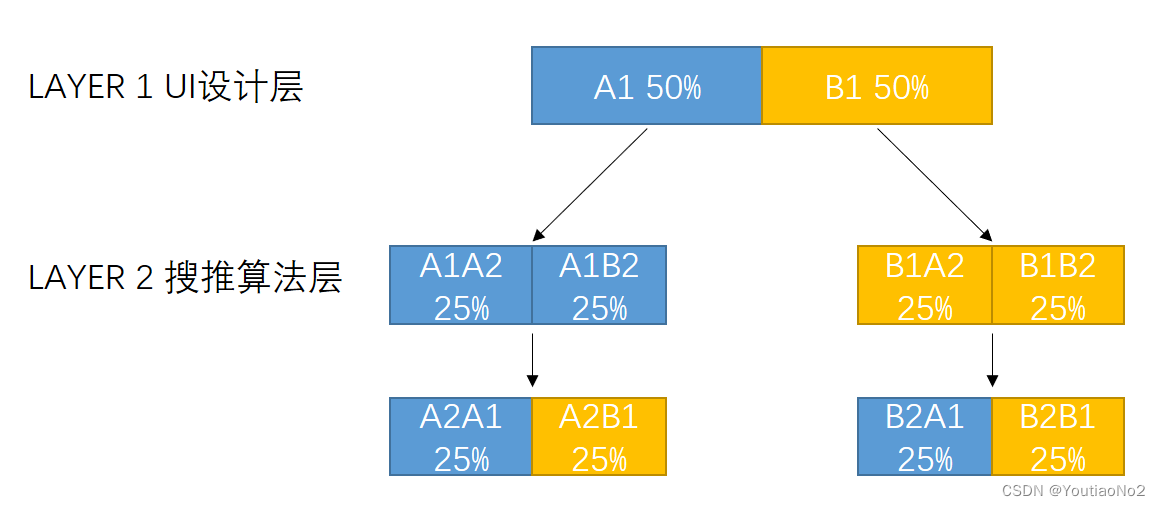
实验分层问题

1. 流量正交要求层与层之间必须相互独立。
2. 同一层可以有多个实验，但流量不能有交集。
3. 一般采用MD5哈希算法来进行ID的分流。

4. 流量分配采用先上小流量，再上大流量的方法进行。

最小样本量计算

均值类

1. 实验采用双边检验，原假设如下：
   $$\begin{array}{r}{H}_0:{\mu }_A-{\mu }_B=0\\ H_1:{\mu }_A-{\mu }_B\ne 0\end{array}$$
2. 样本计算公式如下：
   $$n_A=k{n}_B{n}_B=(1+\frac{1}{k})(\sigma \frac{z_{1-\frac{\alpha }{2}}+z_{1-\beta }}{{\mu }_A-{\mu }_B}{)}^2$$
   其中，${\mu }_B$是当前的数据，${\mu }_A$是预期改进后的数据值。k为$n_A$和$n_B$的比值，这个值一般情况下，我们都默认为1，即AB两组样本量相等，方便做严谨的实验对比，$\sigma$需要根据历史数据估计。
3. 因此，计算均值类指标的最小样本量需要如下变量
   • $\alpha$，显著性水平
   • $\beta$，第二类错误
   • $\delta$，预期提升值(${\mu }_A-{\mu }_B$)
   • $\sigma ,{\mu }_B$，历史均值和标准差

同样的，根据已有的参数，我们也可以估计统计的功效$\beta$是多少，若功效不足，也无法得到实验结论：
$$1-\beta =\Phi (z-z_{1-\frac{\alpha }{2}})+\Phi (-z-z_{1-\frac{\alpha }{2}}),z=\frac{{\mu }_A-{\mu }_B}{\sigma \sqrt{\frac{1}{n_A}+\frac{1}{n_B}}}$$

比值类

1. 实验采用双边检验，原假设如下：
   $$\begin{array}{r}{H}_0:p_A-p_B=0\\ H_1:p_A-p_B\ne 0\end{array}$$
2. 样本计算公式如下：
   $$n_A=k{n}_B{n}_B=(p_B(1-p_B)+\frac{p_A(1-p_A)}{k})(\frac{z_{1-\frac{\alpha }{2}}+z_{1-\beta }}{p_A-p_B}{)}^2$$
   其中，$p_B$是当前的数据，$p_A$是预期改进后的数据值。k为$n_A$和$n_B$的比值，这个值一般情况下，我们都默认为1，即AB两组样本量相等，方便做严谨的实验对比，跟均值有所不同的是，比值类无需计算方差。
3. 因此，计算均值类指标的最小样本量需要如下变量
   • $\alpha$，显著性水平
   • $\beta$，第二类错误
   • $\delta$，预期提升值($p_A-p_B$)
   • $p_B$，历史均值

同样的，根据已有的参数，我们也可以估计统计的功效$\beta$是多少，若功效不足，也无法得到实验结论：
$$1-\beta =\Phi (z-z_{1-\frac{\alpha }{2}})+\Phi (-z-z_{1-\frac{\alpha }{2}}),z=\frac{p_A-p_B}{\sqrt{\frac{p_A(1-p_A)}{n_A}+\frac{p_B(1-p_B)}{n_B}}}$$

4. 在计算得到最小样本量公式后，根据流量的分配及每日流入的用户数，估算需要天数。理论上需要涵盖完整行为周期(视情况而定，有一定的时间成本)。

SRM检验

1. Sample Ratio Mismatch Test，简称样本分流不一致检验。主要检验实验人数分流是否符合预期。
2. 卡方检验：
   • 卡方检验，主要有两种用途。1. 推断总体分布与期望分布是否一致。 (test of goodness-of-fit) 2. 推断两个分类变量是否相关或独立。(test of independence/homogenetity) 实验中，主要用来做第一种检验。
   • 其原假设为：观察频数与期望频数没有差别。
   • 计算公式：
     $${\chi }^2=\sum \frac{(f_o-f_e{)}^2}{f_e}$$
     其中$f_o$为实际观测值，$f_e$为期望值。df 为number of groups - 1。

指标检验

比值类

$$z=\frac{p_1-p_2}{\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}}$$

均值类

1. 首先要进行方差齐性检验：
   $H_0$：对照组和实验组方差一致
   $H_1$：对照组和实验组方差不一致
   $$F=\frac{s_1^2}{s_2^2}$$
   根据F值计算P值，理论上只有在方差一致的情况下才能进行配对t检验。方差不一致时，可以对t检验做一些调整来计算。
2. 两个总体方差未知但相等：
   $$t=\frac{\overline{x_1}-\overline{x_2}}{\sqrt{\frac{s_p^2}{n_1}+\frac{s_p^2}{n_2}}}{s}_p^2=\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}$$
   df 为$n_1+n_2-2$。
3. 两个总体方差未知且不等:
   此时抽样已不服从自由度为$(n_1+n_2-2)$的t分布，而是近似服从自由度为f的t分布，f的计算公式：
   $$f=\frac{(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}{)}^2}{\frac{(\frac{s_1^2}{n_1}{)}^2}{n_1-1}+\frac{(\frac{s_2^2}{n_2}{)}^2}{n_2-1}}t=\frac{\overline{x_1}-\overline{x_2}}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$$
   df为f

关于统计检验显著性问题

1. 在实际业务中，统计指标显著性是一个重要参考，但并非决定因素，还取决于业务上的判断。
2. 关于样本量太大导致实验组和对照组间细微的变化也会显著的解决方案：
   • 计算当前样本量/最小样本量= n， 然后将实验指标的检验变的更加严格， 即使用${\alpha }_{new}=\alpha /n$
   • 在样本中随机采样出最小所需样本量，进行统计分析。
   • 以上均是可能的解决方案，并没有严格的理论支持。

参考资料

• http://powerandsamplesize.com/Calculators/Compare-2-Proportions/2-Sample-Non-Inferiority-or-Superiority
• https://www.microsoft.com/en-us/research/group/experimentation-platform-exp/articles/diagnosing-sample-ratio-mismatch-in-a-b-testing/
• 统计学习方法，贾俊平
• https://www.evanmiller.org/ab-testing/sample-size.html
• https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4296634/