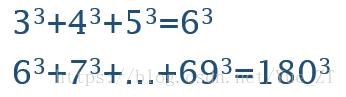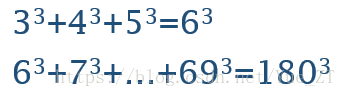编写一个应用程序,验证以下等式是成立的:
提示:if分支语句、for循环语句与C、C++是一样的。
如果能完成上面的验证,则达到基本要求(可得到基本分数8分)。
较高要求,可根据实际情况选做(可得到附加的2分):找到更多的这样的整数:一些相续正整数的立方和正好等于另一个整数的立方。
首先看第一问,编写一个应用程序,验证以下等式是成立的:
问题分析:验证(a^3+(a+1)^3+(a+2)^3+……+b^3)= n^3
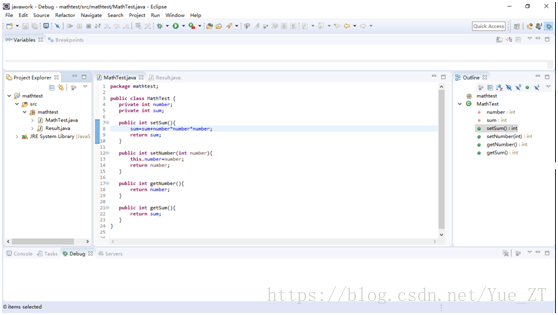
该问很简单,直接上代码,写了两个类
Mathtest类:
packagemathtest;
publicclass MathTest {
privateintnumber;
privateintsum;
publicint setSum(){
sum=sum+number*number*number;
returnsum;
}
publicint setNumber(intnumber){
this.number=number;
returnnumber;
}
publicint getNumber(){
returnnumber;
}
publicint getSum(){
returnsum;
}
}
Result类:
packagemathtest;
importjava.util.Scanner;
publicclass Result {
publicstaticvoid main(String[] args) {
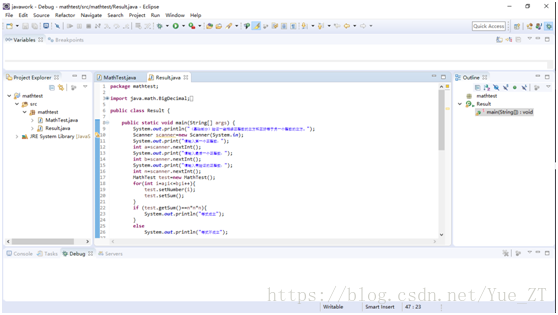
System.out.println("(基础部分)验证一些相续正整数的立方和正好等于另一个整数的立方。");
Scanner scanner=new Scanner(System.in);
System.out.print("请输入第一个正整数:");
inta=scanner.nextInt();
System.out.print("请输入最后一个正整数:");
intb=scanner.nextInt();
System.out.print("请输入需验证的正整数:");
intn=scanner.nextInt();
MathTest test=new MathTest();
for(inti=a;i<=b;i++){
test.setNumber(i);
test.setSum();
}
if (test.getSum()==n*n*n){
System.out.println("等式成立");
}
else
System.out.println("等式不成立");
}
}
上程序截图
上运行截图
再来看拓展目标:找到更多的这样的整数:一些相续正整数的立方和正好等于另一个整数的立方。
问题分析即寻找[k,j]范围内满足(x^3+(x+1)^3+(x+2)^3+……+y^3)= c^3的数
j>=y>=k
//以下为简单思路说明
//整理可求得1^3+2^3+3^3+……+n^3=[n(n+1)/2]^2
//即(1^3+2^3+3^3+……+y^3)-(1^3+2^3+3^3+……+(x-1)^3)表示(x^3+(x+1)^3+(x+2)^3+……+y^3)
//即如果[y*(y+1)/2]^2-[(x-1)*x/2]^2开三次方的结果为一个正整数则等式成立
//说明完毕
上核心代码(思路正确)(结果有错)
System.out.println("寻找【k~j】内满足要求的正整数");
System.out.print("请输入一个正整数j:");
intj=scanner.nextInt();
doublem;
for(floaty=k;y<=j;y++){
for(floatx=1;x<y;x++){
m=(y*(y+1)/2)*(y*(y+1)/2)-((x-1)*x/2)*((x-1)*x/2);
doublec=Math.pow(m,1.0/3);
if (c==(int)c){
System.out.println("第一个整数为:"+(int)x+" 最后一个整数为:"+(int)y);
System.out.println("找到的数为:"+(int)c);
}
}
}