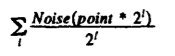参考论文:《An Image Synthesizer》 Ken Perlin
如果你是游戏玩家,你也许曾在游戏风景中驻足,并仔细观察草木和岩石的贴图,并感叹于它那看似杂乱而又自然的纹脉。你未必会知道,这里面的很多纹理,并不是美工一个个像素填出来的,也不是相机拍摄出来的,而是由代码自动生成的。同样,波澜起伏的地面或海洋,也不一定完全是手工制作的高度图,而同样依赖于代码的力量,也就是我们接下来要介绍的柏林噪声。
柏林噪声旨在描述自然中的随机效果,它创建的纹理可以直接运用于顶点着色器,而不是生成一张纹理图,然后用传统的纹理映射技术把贴图附加到一个三维物体上。
这也就相当于,纹理将不需要适应表面,我们只需要提供每个顶点的(x,y,z)的坐标,传入柏林噪声函数Noise(),计算得到一个随机数,然后与原颜色运算,得到新的颜色,如同直接在物体表面绘制纹理一样。
这意味着我们应用柏林噪声的代码最好采用着色器,直接把颜色运算之后传给顶点着色器。
那么,问题的关键就在于这个Noise()应该是怎样的,perlin认为,噪声函数应当满足以下性质:
| 1. 旋转统计不变性。(不管我们怎么旋转它的域,它都有同样的统计特性) 2. 频率带通有一定界限。(它没有明显的大或者小的特征,而是在一定范围内) 3. 平移统计不变性。(不管我们如何平移它的域,它都有同样的统计特性) |
这也就意味着,我们可以在不同的视觉尺度上创建所需表面的随机特性。
噪声的生成步骤:
1.预处理:考虑x,y,z空间中所有点的集合(坐标为整数),我们称这个集合为整数格。现在我们为整数格的每个点附一个(x,y,z)上的伪随机梯度值,也就是一个向量,并且要将其 处理成单位向量。
perlin给出的计算方法如下 :
对于每个顶点先随机生成一个向量(比如调用C库中的rand()),然后将这个下标固定地映射到另外一个下标上,取另外一个下标对应的顶点向量。如果是二维或三维,这个过程就要重复2次,具体过程可以看之后的代码。
2.如果(x,y,z)处在整数格上,那么此处的噪声就是d。
3.如果(x,y,z)不在整数格上,我们计算光滑插值系数。
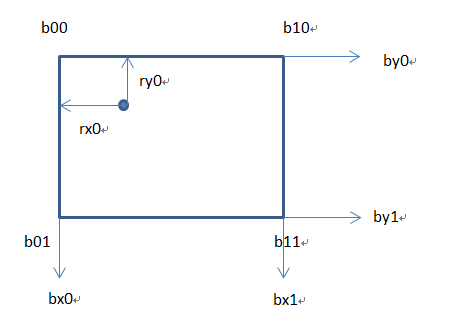
具体的方法如下,以二维为例,我们要找到这个点周围的四个整数点,然后我们得到四个值,横坐标为bx0 ~ bx1,纵坐标为by0 ~ by1。点到bx0在x轴上的距离为rx0,到by0在y轴上的距离为ry0。
perlin给出了一个缓和曲线使得线性插值连贯。
能使得一阶导数连续的缓和曲线函数 (最初的版本) : s_curve(t) ( t * t * (3. - 2. * t) )
能使得二阶导数连续的缓和曲线函数 (更新的版本) : s_curve(t) ( t * t * t * (6 * t * t - 15 * t + 10) )
之后分别将rx0和ry0传入缓和曲线,得到一个新的值sx和sy。
接下来做一个双线性插值,sx和sy就是第一步线性插值的系数,但是计算得到系数之后,我们还需要插值的起点和终点。他们的计算方法如下:
(1)求(rx0,ry0)与左上角点的梯度b00的点乘,得到起点u,求(rx0 + 1,ry0)与右上角点的梯度b10的点乘,得到终点v,以uv为两端,sx为插值系数,做线性插值,得到a
(2)求(rx0,ry0 + 1)与左下角点的梯度b01的点乘,得到起点u,求(rx0 + 1,ry0 + 1)与右下角点的梯度b11的点乘,得到终点v,以uv为两端,sx为插值系数,做线性插值,得到b
( 3 ) 最终,对a和b进行线性插值,插值系数为sy,得到最终的结果。
以上算法步骤中,先对x轴还是先对y轴插值其实是无所谓的。
最终得到的柏林噪声分布在 -1 ~ 1之间,我们可以把它映射到我们需要的颜色区别(比如0 ~ 255 或 0 ~ 1)得到对应的颜色。
应用
计算得到噪声之后,我们可以做一些简单的应用,比如创建一个简单的随机表面纹理:
color = white * Noise(point)
上式中的point也就是点的坐标。
这样的效果如下,这张图具有较窄的带宽,它的细节仅仅分布特定区间内,也就是说,纹理的频谱没有一些中心峰的频率。关于生成这些图的代码会在后面给出。两张图仅仅是参数不同的区别,它们都是由柏林噪声生成的。


Perlin给出的官方例程的噪声生成结果
生成以上基础柏林噪声纹理的代码会在后面给出,之后的一些变形都是在Noise()函数的基础上得到的,可以根据perlin给定的一些公式自己尝试实现这些效果。当然也可以自己试着模拟一些效果。
当然,我们还可以做点别的。比如当我们可能想要不同范围的值,映射到不同的颜色上:
color = Colorful(Noise(k*point)
我们通过乘以一个常量k,就可以得到不同尺度上的纹理,这么描述似乎有些晦涩,我们可以看一下最终的效果:
可以看到这个脉络和最简单的柏林噪声图是类似的,只不过我们把特定区间的rgb映射到了一个颜色上。(通过Colorful函数)
我们把描述Noise()在x,y,z上各自的变化率(梯度)的函数为DNoise()。
假如我们想制作一个凹凸纹理贴图,我们也可以在原有法线(normal)上加一些噪声的扰动,以做出凹凸的效果。在有了DNoise()之后,这样的行为变得非常方便:
normal = normal + Dnoise(point)
最终的效果图如下:
我们来一些更有意思的。
我们可以加入一个1/f波动,通过以下公式来模拟这个信号(把不同频率的octave叠加以得到更为真实的效果):
以上1/f频谱函数的微分是一个单调频谱的函数,因此我们可以同时在所有的octave内创建类似的法线扰动,它的伪代码如下:
f = 1
while f < pixel_freq
normal += Dnoise ( f * point )
f *= 2
这个算法在计算到像素级别后停止。以上这些算法都是逐像素独立的,也就是说计算一个像素颜色不需要依赖于其它像素,所以我们可以并行地计算每个像素,然后大幅度提升运行速度。
大理石纹理
我们注意到大理石的有着各种各样的层次,我们可以用正弦波来做一个简单的色彩滤镜:
function boring_marble(point)
x = point[1]
return marble_color(sin(x))
上式中,Point[1]是point的第一个分量(x),而marble_color()是一个样条曲线函数,它可以把一个数映射到一个色彩向量上。
想要模拟更真实的大理石,可以加一个扰动:
function marble(point)
x = point[1] + turbulence(point)
return marble_color(sin(x))
而这个扰动turbluence()函数,可以通过Noise()得到,它的具体算法如下:
function turbulence(p)
t = 0
scale = 1
while( scale > pixelsize)
t += abs(Noise(p/scale) * scale)
scale /= 2
return t
水纹理
假设我们想要模拟波浪的表面,为了简单起见,我们使用法线扰动,而不是修改表面点的值。
我们使用球面波来做这件事,对于每个波浪中心,我们将会通过一个表面到中心的圆的函数来扰动表面法线。
normal += wave ( point - center)
function wave (v)
return direction(v) * cycloid (norm (v))
我们可以使用某一集合的点的Doise()的方向,产生随机分布的单位球体,来创建多个中心。
function makewaves(n)
for i in [ 1 .. n ]
center [i] = direction (Dnoise ( i * [100 0 0] ))
return center
比如如果我们想要创建一个有20个源的波浪,我们可以这样调用:
if begin_frame
center = makewaves(20)
for c in center
normal += wave (point - c)
用20的参数做出的效果:
如果想要做出更逼真的波浪效果,可以加入一个1/f扰动。如果对每个中心加一个随机的频率f,那么这个程序的最后一行将替换为:
normal += wave ((point - c) * f ) / f
此外,我们还需要让波浪随着时间动起来:
function moving_wave (v ,Dphase)
return direction(v) * cycloid (norm(v) - frame * Dphase)
Dphase就是相变的速度,一个可以让效果比较真实的参数是f^(1/2)。
做出的波浪效果:
perlin的个人主页中给出了基本Noise()函数的代码,以下只截取了二维部分,加入绘制部分,更详细的代码可以参考以下链接,点击打开链接
#include <stdlib.h>
#include "gl/glut.h"
#include <stdio.h>
#include <time.h>
#include <math.h>
#define B 0x100 //256
#define BM 0xff //255
#define N 0x1000 //4096
#define NP 12 // 2^N
#define NM 0xfff
static int p[B + B + 2];
static float g2[B + B + 2][2];
int start = 1;
static void init(void);
//#define s_curve(t) ( t * t * (3. - 2. * t) )
#define s_curve(t) ( t * t * t * (t * (t * 6. - 15.) + 10.) )
#define lerp(t, a, b) ( a + t * (b - a) )
#define setup(i,b0,b1,r0,r1)\
t = vec[i] + N; \
b0 = ((int)t) & BM; \
b1 = (b0 + 1) & BM; \
r0 = t - (int)t; \
r1 = r0 - 1.;
float noise2(float vec[2])
{
int bx0, bx1, by0, by1, b00, b10, b01, b11;
float rx0, rx1, ry0, ry1, *q, sx, sy, a, b, u, v, t;
register int i, j;
if (start){
start = 0;
init();
}
setup(0, bx0, bx1, rx0, rx1);
setup(1, by0, by1, ry0, ry1);
i = p[bx0];
j = p[bx1];
b00 = p[i + by0];
b10 = p[j + by0];
b01 = p[i + by1];
b11 = p[j + by1];
sx = s_curve(rx0);
sy = s_curve(ry0);
#define at2(rx,ry) ( rx * q[0] + ry * q[1] )
q = g2[b00]; u = at2(rx0, ry0);
q = g2[b10]; v = at2(rx1, ry0);
a = lerp(sx, u, v);
q = g2[b01]; u = at2(rx0, ry1);
q = g2[b11]; v = at2(rx1, ry1);
b = lerp(sx, u, v);
return lerp(sy, a, b);
}
static void normalize2(float v[2])
{
float s;
s = sqrt(v[0] * v[0] + v[1] * v[1]);
v[0] = v[0] / s;
v[1] = v[1] / s;
}
static void init(void)
{
int i, j, k;
for (i = 0; i < B; i++) {
p[i] = i;
for (j = 0; j < 2; j++)
g2[i][j] = (float)((rand() % (B + B)) - B) / B;
}
while (--i) {
k = p[i];
p[i] = p[j = rand() % B];
p[j] = k;
}
for (i = 0; i < B + 2; i++){
p[B + i] = p[i];
for (j = 0; j < 2; j++)
g2[B + i][j] = g2[i][j];
}
}
void drawScene()
{
float d1 = -300.0, d2 = -300.0;
const float size = 0.1f;
for (int i = 0; i < 100; i++) {
d1 = -300;
for (int j = 0; j < 100; j++) {
float vec[2] = { d1,d2 };
float color = (noise2(vec) + 1)/4;
glColor3f(color,color,color);
glRectf(i*size, j*size, i*size + size, j*size + size);
d1 += 0.1;
}
d2 += 0.1;
}
}
void reshape(int width, int height)
{
if (height == 0)height = 1;
glViewport(0, 0, width, height);
glMatrixMode(GL_PROJECTION);//设置矩阵模式为投影
glLoadIdentity(); //初始化矩阵为单位矩阵
glOrtho(0, 10,0,10, -100, 100); //正投影
glMatrixMode(GL_MODELVIEW); //设置矩阵模式为模型
}
void redraw()
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);//清除颜色和深度缓存
glMatrixMode(GL_MODELVIEW);
glLoadIdentity(); //初始化矩阵为单位矩阵
drawScene();//绘制场景
glutSwapBuffers();//交换缓冲区
}
int main(int argc,char* argv[])
{
srand(time(nullptr));
glutInit(&argc, argv);//对glut的初始化
glutInitDisplayMode(GLUT_RGBA | GLUT_DEPTH | GLUT_DOUBLE);
glutInitWindowSize(400, 400);//设置窗口大小
int windowHandle = glutCreateWindow("Perlin Noise");//设置窗口标题
glutDisplayFunc(redraw); //注册绘制回调函数
glutReshapeFunc(reshape); //注册重绘回调函数
glutMainLoop(); // glut事件处理循环
}