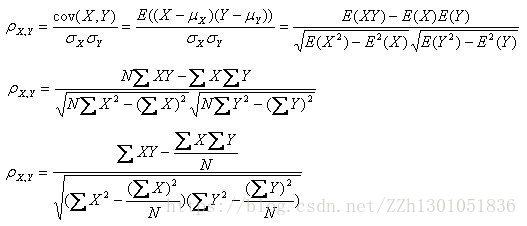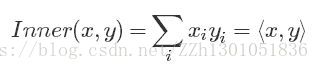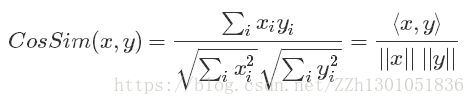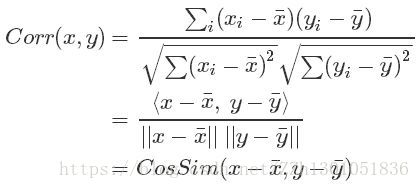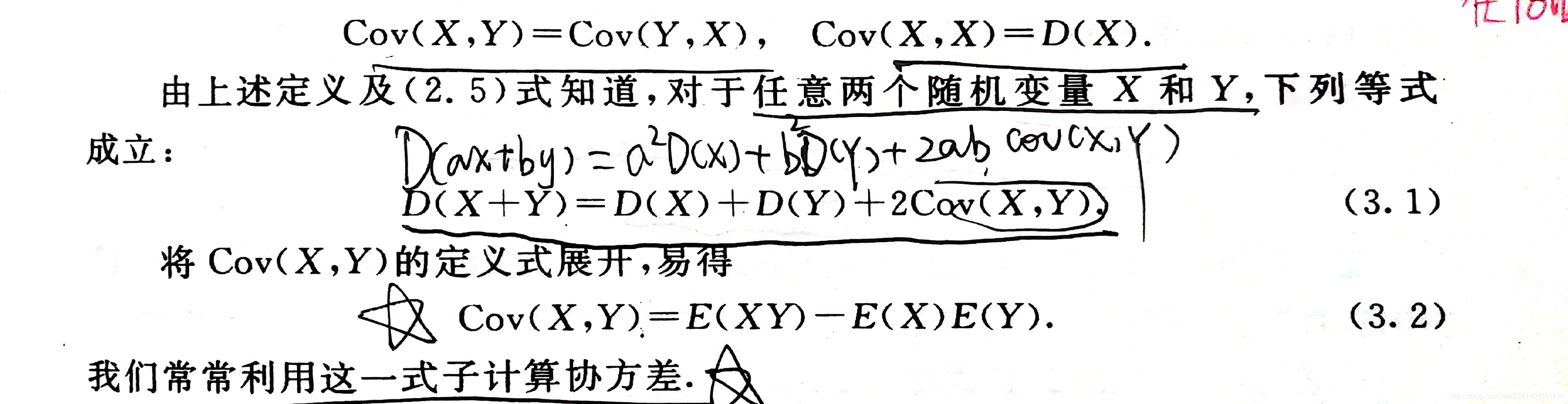一、相关系数第一次理解
概念:Pearson相关系数 (Pearson CorrelationCoefficient)是用来衡量两个数据集合是否在一条线上面,它用来衡量定距变量间的线性关系。[1]
注:
【定距变量】[2][3]
若想理解定距变量,需要与其他变量类型进行比对。
统计学依据数据的计量尺度将数据划分为四大类 ,即定距型数据、定序型数据、定类型数据和定比型数据。
- 定距型数据是数字型变量,可以求加减平均值等,但不存在基准0值,即当变量值为0时不是表示没有,如温度变量,当温度为0时,并不是表示没有温度,这样温度就为定距变量,而不是定比变量。
- 定序型数据具有内在固有大小或高低顺序,如职称变量可以有低级、中级和高级三个取值,可以分别用1、2、3等表示。有大小或高低顺序,但数据之间却是不等距的,因为低级和中级职称之间的差距与中级和高级职称之间的差距是不相等的,因此可以排序,但不能加减。
- 定类型数据是指没有内在固定大小或高低顺序,如性别男和女;
- 定比型变量就是常说的数值变量,既有测量单位,也有绝对零点。例如职工人数,身高。
线性关系
【线性关系】[4]
两个变量之间存在一次方函数关系,就称它们之间存在线性关系。正比例关系是线性关系中的特例,反比例关系不是线性关系。更通俗一点讲,如果把这两个变量分别作为点的横坐标与纵坐标,其图象是平面上的一条直线,则这两个变量之间的关系就是线性关系。即如果可以用一个二元一次方程来表达两个变量之间关系的话,这两个变量之间的关系称为线性关系。
线性关系的显著特征是图像为过原点的直线(没有常数项的情况下,如:y=kx+jz,(k,j为常数,x,z为变量);而当图像为不过原点的直线时,函数称为直线关系。线性关系与直线关系是不同的,经常被大家混淆。
线性关系的函数具备如下特点:
(1)每一项(常数项除外)的次数必须是一次的(这是最重要的)。如:x=y+z+c+v+b。如果出现平方,这些就肯定不是线性关系。
如果每项的次数不是一次就不是线性关系:x=yz(这里假定y,z是变量而不是常数),那么x与y,或x与z就不是线性关系。
(2)常数对是否构成直线关系没影响(假定常数不为0)如:x=ky+l*z+a。
用途:[5] pearson系数用来描述两组线性的数据一同变化移动的趋势。
公式:[5]
用数学公式表示,皮尔森相关系数等于两个变量的协方差除于两个变量的标准差。
X、Y线性相关时,两个变量的协方差等于两个变量各自标准差的乘积,此时皮尔森相关系数为1。
公式理解:
值域:[-1,1]
使用情况:
Pearson相关系数常用于基于用户的推荐系统,比其他对比用户的方法更胜一筹。(相对的,在基于物品的推荐系统中,常使用余弦相似度方法。)[6]
由于pearson描述的是两组数据变化移动的趋势,所以在基于user-based的协同过滤系统中,经常使用。描述用户购买或评分变化的趋势,若趋势相近则pearson系数趋近于1,也就是我们认为相似的用户。[5]
缺陷:笔者尚未理解明白,所以只粘贴原文了。
(1)存在一些所有人都喜爱的物品,让两个用户对有争议的物品达成共识会比对广受欢迎的物品达成共识更有价值,但Pearson这样的相似度方法无法将这种情况考虑在内。[6] Page10
(2)某博主关于重叠项的思考。 [5]
该部分如有了解的朋友,还请留下指点,不胜感谢。
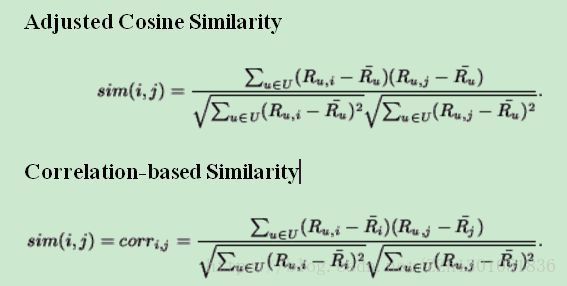
皮尔森系数与修正余弦相似度的区别:[8]
两者在公式形式上极其相似,所以需要进行对比区分。
由于没有实际应用过,尚且没有明白透彻,所以此处只提几点表面上的理解。
两者计算的形式很类似,但是有具体的细节差别,在分母和分子上都有体现。归纳起来:差别就在去中心化的方式上。
修正余弦公式和皮尔森相关系数公式都是针对item-based CF计算item-item之间相似性的,所以修正余弦公式减去了用户的打分均值,皮尔森相关系数公式减去了item得分均值。(换句话说,修正cosine考虑的是对item i打过分的每个user u,其打分的均值,Pearson考虑的是每个item i 的被打分的均值。)
两者为什么要去中心化呢?(两种方式减去均值)
(1)修正cosine相似度的目的是解决cosine相似度仅考虑向量维度方向上的相似而没考虑到各个维度的量纲的差异性,所以在计算相似度的时候,做了每个维度减去均值的修正操作。
(2)Pearson correlation 相关系数主要考虑线性相关性,定义为两个变量之间的协方差和标准差的商,所以自然的考虑了均值的修正操作。
简便记忆方法
可以看出,公式比较长,可以使用点积进行记忆。公式形式上简单后,也更便于理解。
各种相似度与点积关系的推演:
cosine相似度,其实就是归一化后的点积结果,
Pearson相关系数是去中心化&归一化的点积结果
修正cosine相似度,也是去中心化&归一化的点积结果,与Pearson的差别就在于去中心化的差异(上面描述的)
公式参考如下:
点积:
cosine相似度:
Pearson相关系数:
##参考文献
[1] Pearson相关系数_百度百科
[2] 定距变量_百度百科
[3] 举例说明定类数据,定序数据,定距数据和定比数据的区别_百度知道
[4] 线性关系_百度百科
[5] Pearson 相关系数–最佳理解及相关应用-CSDN博客
[6] 《推荐系统 》书籍 Dietmar Jannach, Markus Zanker etc 蒋帆译
[7] 皮尔森相关系数及原理_smilingflowers
[8] 修正余弦相似度和皮尔森系数什么关系?- 知乎
二、相关系数第二次理解
相关系数可以看做协方差
2.1 协方差
概率论和统计学中的协方差,评估两个向量如何一起变化,通俗的说,即是否同时偏离均值。
考虑两个数值属性A、B和n次观测的集合{(a1,b1),…,(an,bn)},A、B的均值又称为A、B的期望值。
A、B的协方差定义为:
Cov(A,B)=E((A -
A
‾
\overline{A}
A)(B -
B
‾
\overline{B}
B))
可以看出,当A、B同时大于或小于均值时,协方差为正数;当一个大于均值,一个小于均值时,协方差为负数。
协方差的作用、缺点、及改进。
作用:在A、B量纲相同时,协方差对描述X、Y的相关程度有一定作用。
具体的,当A、B不相关(即独立)时,E(A
⋅
\cdot
⋅B) = E(A)E(B),所以,协方差Cov(A,B) = E(A
⋅
\cdot
⋅B) -
A
‾
\overline{A}
A
B
‾
\overline{B}
B = 0。然而,反过来不成立。
所以,上面才说,只有“一定作用”。。。而已。真正判断两个变量的相关性,还是得用Pearson相关系数鸭!
缺点:在A、B量纲不同时,协方差在数值上差异很大。
改进:为了解决上述缺点,将协方差除以A的标准差和B的标准差,从而剔除量纲的影响。这便是后来引入的Pearson相关系数。
2.2 Pearson 相关系数
又叫Pearson积矩系数、协相关系数,表示为rA,B。
公式即
rA,B = Cov(A,B) /
σ
A
\sigma{A}
σA
σ
B
\sigma{B}
σB
相关系数作用:
在描述两个变量的相关性上,协方差的作用有限。
相关系数比协方差更好,因为相关系数剔除了量纲的影响。并且
相关系数 > 0 ,变量正相关;
相关系数 < 0 ,变量负相关;
相关系数 = 0 ,变量不相关;
可以看出,描述两个变量的相关性时,相关系数的作用更全面。
参考文献:
[1] [统计学理论基础] 协方差与相关系数
[2] 协方差-百度百科
三、协方差和相关系数 第三次理解
3.1 协方差、相关系数的前提
-
数学期望的一个重要性质是:
设X、Y是两个随机变量,则- E(X+Y)=E(X)+E(Y)
- E(XY)=E(X)E(Y)
-
方差的定义是:
D(X) = E{[X - E(X)]2}
注:
方差描述随机变量X与其均值的偏离程度,所以直观上应为E{|X-E(X)|}。
但上式带有绝对值,运算不方便,为了数学计算上的方便,使用平方代替绝对值E{[X-E(X)]2}
- 方差的一个重要性质是:
设X、Y是两个随机变量,则 D(X+Y) = D(X)+D(Y)+2E[ (X-E(X)) (Y-E(Y)) ]。
证明:
将上面的结论摘录下来,即:
D(X+Y) = D(X) + D(Y) + 2E{ [X-E(X)] [Y-E(Y)] }
E{[X-E(X)] [Y-E(Y)]} = E(XY)-E(X)E(Y)
由数学期望的性质2 (E(XY) = E(X)E(Y))知,若随机变量X、Y相互独立,则:
注意:该公式将成为推导协方差和相关系数的源头
故D(X+Y)=D(X)+D(Y)。
3.2 协方差和相关系数
3.2.1 协方差和相关系数的定义
由3.1方差性质的证明中,可以看到,若两个随机变量相互独立,则
协方差和相关系数的定义:
3.2.2 协方差和相关系数 为什么能表示两个随机变量的相关性
参考博客:协方差为什么能表示两个随机变量的相关性?
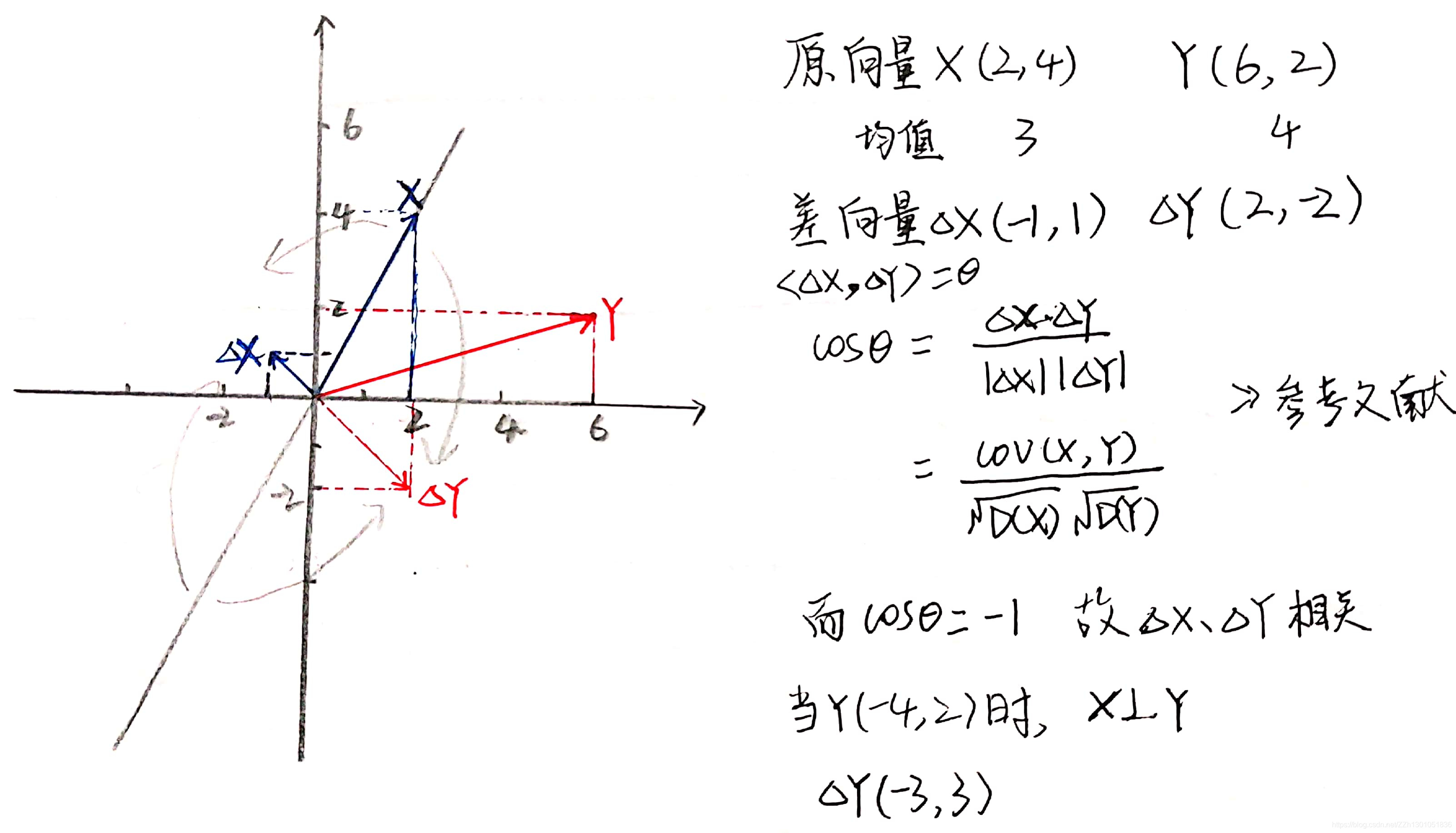
证明的主旨思想使用了 两个向量的夹角的余弦:
两个不相关,那么他们的夹角为90度,相关,则夹角小于90度。
笔者在测试这一证明时,遇到一个问题,即图中,有一条与向量X重合的黑线L:L左上方的向量Y们,其差向量的方向,全指向(-1,1)方向,只是长度不同,这些向量Y们与X的相关系数cosθ = 1;L右下方的向量Y们,其差向量的方向,全指向(1,-1)方向,只是长度不同,这些向量Y们与X的相关系数cosθ = -1;只有(1,1)方向的向量,其差向量才与X,垂直,此时cosθ = 0。
也就是说,照这样推导,不管X是什么向量,只有(1,1)方向的向量与之不相关,其他向量都是或者正相关,或者负相关。
23333333333333,我到底错在哪里了??????感觉自己绕进了某一个圈里,请求看到这儿的朋友指点迷津鸭!!!!!!!!!!!
3.2.3 协方差矩阵
X、Y的协方差矩阵,由X、Y的方差和协方差组成: