前言
- 课本: 编译原理(第三版)[王生原、董渊…等编著]
- 习题: 主要习题内容是第一章到第八章,具体内容如下表
| 章节 | 内容 | 链接 |
|---|---|---|
| 第一章 | 课后部分选择题 | https://blog.csdn.net/Zchengjisihan/article/details/136243955 |
| 第二章 | 课后部分选择题 | https://blog.csdn.net/Zchengjisihan/article/details/136243955 |
| 第三章 | 课后习题1(4)、5、9 | https://blog.csdn.net/Zchengjisihan/article/details/136264182 |
| 第四章 | 课后习题1、2、3 | https://blog.csdn.net/Zchengjisihan/article/details/136264485 |
| 第五章 | 课后习题1、4 | https://blog.csdn.net/Zchengjisihan/article/details/136264816 |
| 第六章 | 课后习题11、15 | https://blog.csdn.net/Zchengjisihan/article/details/136276626 |
| 第七章 | 课后习题2 | https://blog.csdn.net/Zchengjisihan/article/details/136277222 |
| 第八章 | 课后习题1 | https://blog.csdn.net/Zchengjisihan/article/details/136277222 |
1. 对文法G[S]
S → a ∣ ∧ ∣ ( T ) S\to a|\wedge|(T) S→a∣∧∣(T)
T → T , S ∣ S T\to T,S|S T→T,S∣S
(1)给出 ( a , ( a , a ) ) (a,(a,a)) (a,(a,a))和 ( ( ( a , a ) , ∧ , ( a ) ) , a ) (((a,a), \wedge ,(a) ),a) (((a,a),∧,(a)),a)的最左推导
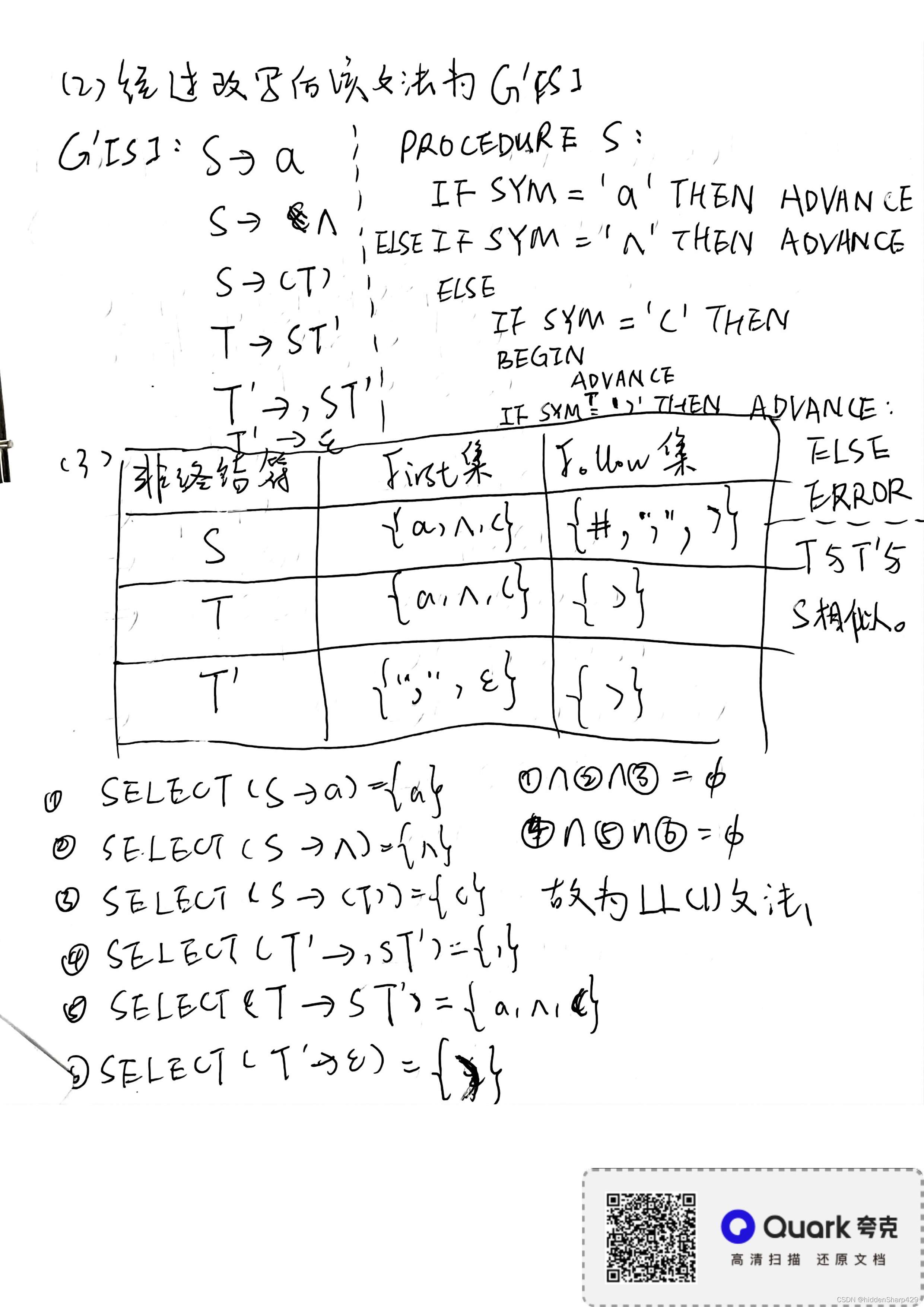
(2)对文法G进行改写,然后对每个非终结符写出不带回溯的递归子程序
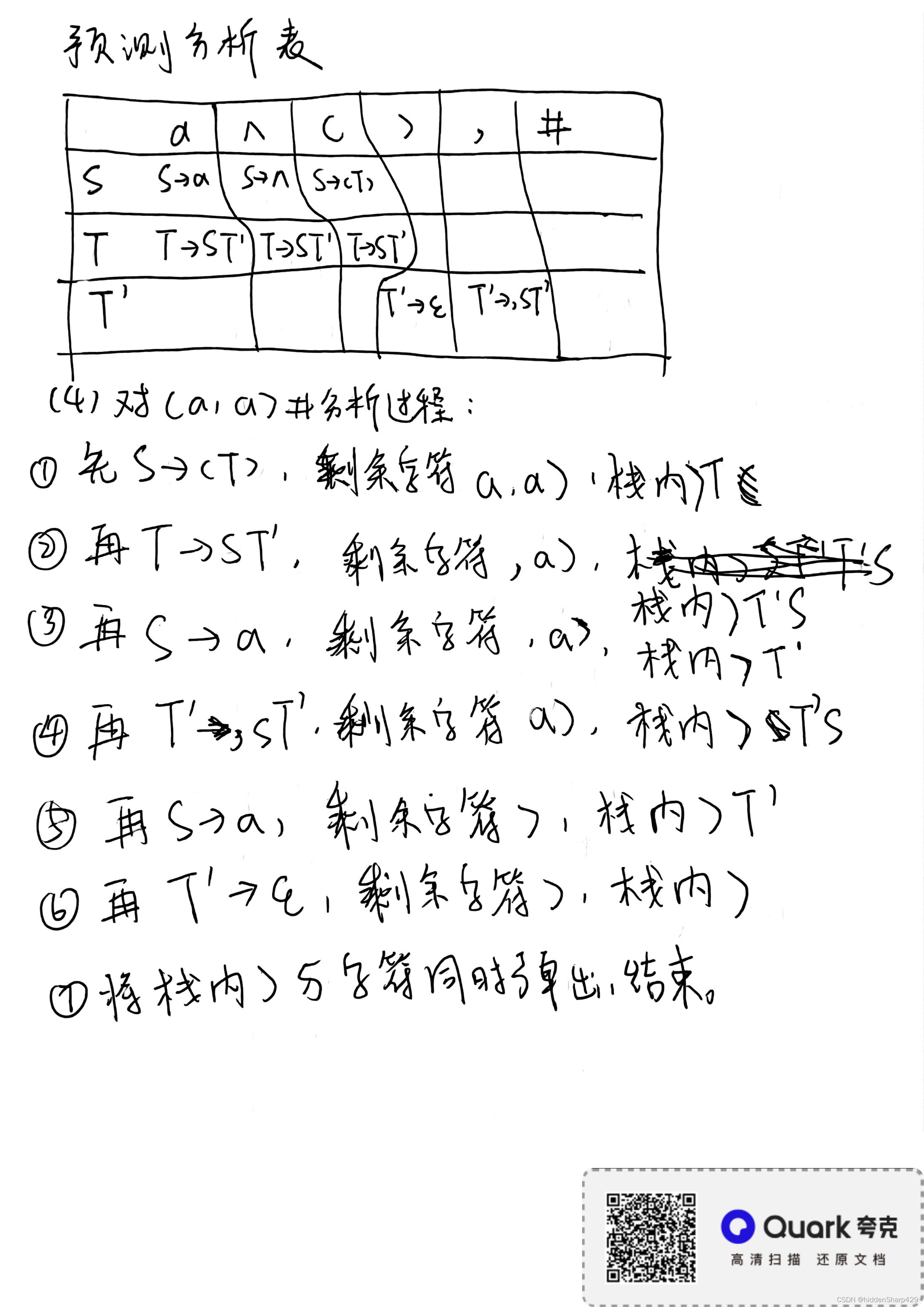
(3) 经改写后的文法是否是LL(1)的?给出它的预测分析表
(4) 给出输入串 ( a . a ) # (a.a)\# (a.a)#的分析过程,并说明该串是否为G的句子
2. 对下面的文法G
E → T E ′ E\to TE' E→TE′
E ′ → + E ∣ ϵ E'\to +E|\epsilon E′→+E∣ϵ
T → F T ′ T\to FT' T→FT′
T ′ → T ∣ ϵ T'\to T|\epsilon T′→T∣ϵ
F → P F ′ F\to PF' F→PF′
F ′ → ∗ F ′ ∣ ϵ F'\to *F'|\epsilon F′→∗F′∣ϵ
P → ( E ) ∣ a ∣ b ∣ ∧ P\to (E)|a|b|\wedge P→(E)∣a∣b∣∧
(1)给计算这个文法每个非终结符的FIRST集和FLLOW集
(2)证明这个文法是LL(1)的
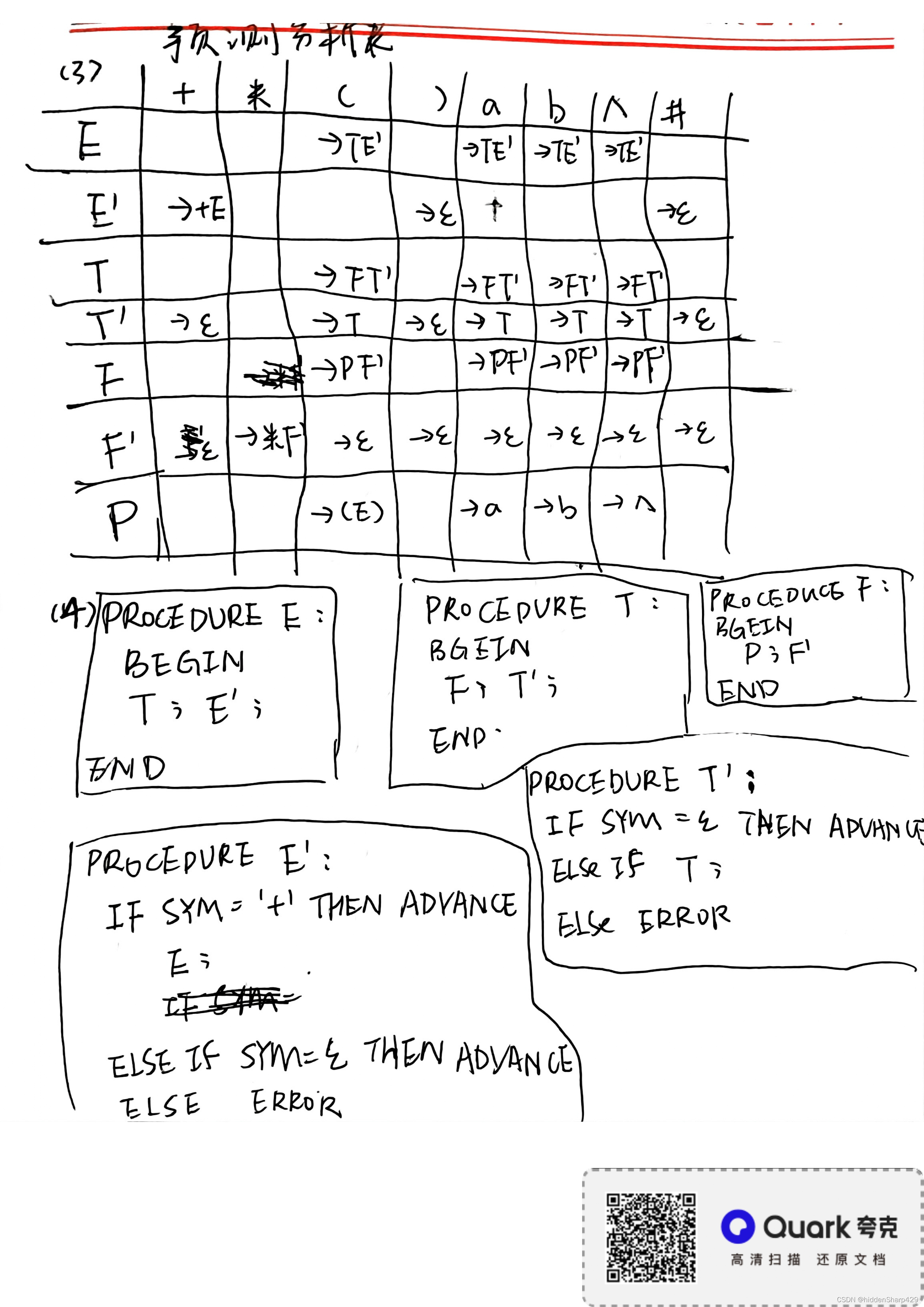
(3) 构造它的预测分析表
(4) 构造它的递归下降分析程序
3. 已知文法G[S]
S → M H ∣ a S\to MH|a S→MH∣a
H → L S o ∣ ϵ H\to LSo|\epsilon H→LSo∣ϵ
K → d M L ∣ ϵ K\to dML|\epsilon K→dML∣ϵ
L → e H f L\to eHf L→eHf
M → K ∣ b L M M\to K|bLM M→K∣bLM
判断G是否是LL(1)文法,如果是,构造LL(1)分析表
结束语
如果有疑问欢迎大家留言讨论,你如果觉得这篇文章对你有帮助可以给我一个免费的赞吗?我们之间的交流是我最大的动力!