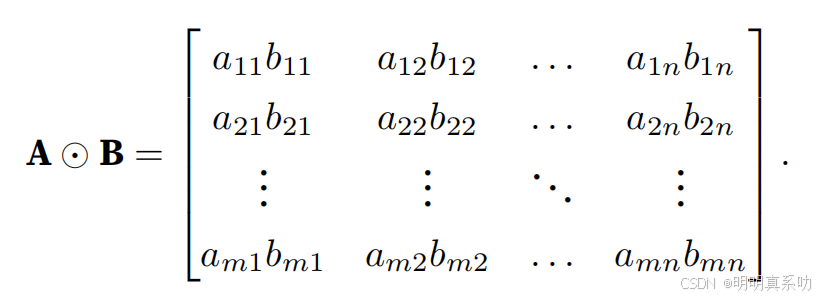摘要

本文深入探讨了深度学习中的数学基础，特别是线性代数的核心概念。文章从标量、向量、矩阵和张量的定义和性质出发，逐步介绍了它们在深度学习中的应用。通过详细的代码示例和数学公式，本文展示了如何进行基本的算术运算、矩阵操作、点积、范数计算等关键操作。文章还讨论了降维技术，包括求和和平均值计算，以及它们在数据压缩和特征提取中的重要性。

Abstract

This paper delves into the mathematical foundations of deep learning, with a particular focus on the core concepts of linear algebra. Starting from the definitions and properties of scalars, vectors, matrices, and tensors, the paper gradually introduces their applications in deep learning. Through detailed code examples and mathematical formulas, the paper demonstrates how to perform basic arithmetic operations, matrix operations, dot products, and norm calculations. The paper also discusses dimensionality reduction techniques, including sum and average calculations, and their importance in data compression and feature extraction.

一、动手深度学习

1. 线性代数

1.1 标量

在数学上，我们通常将仅包含单个数值的量称为标量。
要将华氏度转换为摄氏度，我们可以使用以下公式：
$$c=\frac{5}{9}(f-32)$$
其中， f 代表华氏度温度，比如52。
在这个等式中，5、9和32都是标量值。变量 c 和 f 代表未知的标量值。

我们采用了标准的数学表示法，其中标量变量通常用小写字母表示，如 x 、 y 和 z 。
$$我们用\mathbb{R}来表示所有连续实数标量的空间。$$

虽然我们稍后会详细定义“空间”的概念，但目前你只需知道
$$x\in \mathbb{R}，表示x是一个实数标量的正式表达方式。$$
$$符号\in 表示“属于”，意味着x是某个集合的成员。$$

例如，

$$x,y\in 0,1。表示x和y只能是0或1。$$

标量可以用只有一个元素的张量来表示。
在接下来的代码示例中，我们将创建两个标量，并展示一些基本的算术运算，包括加法、乘法、除法和指数运算。

import torch

x = torch.tensor(3.0)
y = torch.tensor(2.0)
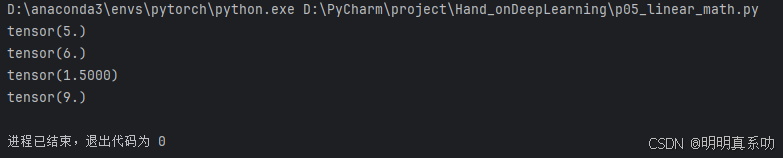
print(x + y)
print(x * y)
print(x / y)
print(x ** y)

1.2 向量

向量可以被视为由标量值组成的有序列表，其中每个标量值都是向量的一个元素或分量。
在数据科学和机器学习中，向量常用于表示数据集中的单个样本，每个分量都具有实际的业务或研究意义。
举个例子：

1. 以贷款违约风险预测模型为例，我们可能会为每位贷款申请人创建一个向量，向量的每个分量分别代表申请人的收入水平、工作年限、历史违约次数等关键信息。
2. 在医疗领域，如果我们分析患者心脏病发作的风险，我们可能会构建一个向量来描述每位患者，其分量可能包括患者的生命体征、胆固醇水平、日常运动时间等健康相关数据。

在数学表示中，向量通常用粗体小写字母表示，例如 x、y 和 z。向量本质上是一维张量，其长度可以非常长，理论上只受限于计算机的内存容量。

x = torch.arange(4)
print(x)

我们可以使⽤下标来引⽤向量的任⼀元素。例如，我们可以通过x_i来引⽤第i个元素。
例如，我们可以通过x_i来引⽤第i个元素。
注意，元素xi是⼀个标量，所以我们在引⽤它时不会加粗。大多数人认为列向量是向量的默认⽅向
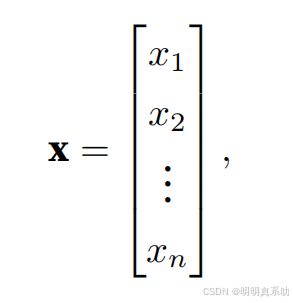
所以向量x可以写为：

其中x1, . . . , xn是向量的元素。
在代码中，我们通过张量的索引来访问任⼀元素。

import torch
x = torch.arange(4)
print(x)
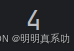
print(x[3])

向量只是⼀个数字数组，就像每个数组都有⼀个⻓度⼀样，每个向量也是如此。
⼀个向量x由n个实值标量组成，我们可以将其表⽰为x ∈ R_n。
向量的⻓度通常称为向量的维度（dimension）。
与普通的Python数组⼀样，我们可以通过调⽤Python的内置len()函数来访问张量的⻓度。

print(len(x))

当⽤张量表⽰⼀个向量（只有⼀个轴）时，我们也可以通过.shape属性访问向量的⻓度。
形状（shape）是⼀个元素组，列出了张量沿每个轴的⻓度（维数）。对于只有⼀个轴的张量，形状只有⼀个元素。

print(x.shape)

向量或轴的维度被⽤来表⽰向量或轴的⻓度，即向量或轴的元素数量。
然⽽，张量的维度⽤来表⽰张量具有的轴数。
在这个意义上，张量的某个轴的维数就是这个轴的⻓度。

1.3 矩阵

正如向量将标量从零阶推⼴到⼀阶，矩阵将向量从⼀阶推⼴到⼆阶。
矩阵，我们通常⽤粗体、⼤写字⺟来表⽰（例如，X、Y和Z），在代码中表⽰为具有两个轴的张量。
在数学表⽰法中，我们使⽤A ∈ R^m×n 来表⽰矩阵A，其由m⾏和n列的实值标量组成。
我们可以将任意矩阵A ∈ R,m×n视为⼀个表格，其中每个元素a_i,j属于第i⾏第j列：

import torch
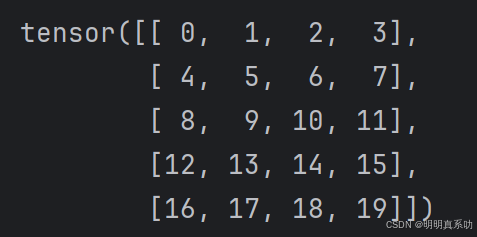
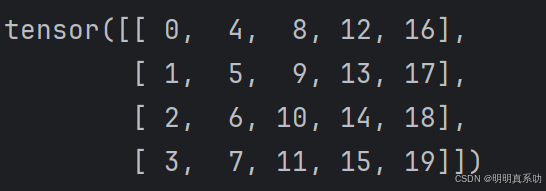
A = torch.arange(20).reshape(5, 4)
print(A)

在代码中访问矩阵的转置。

A.T

作为⽅阵的⼀种特殊类型，对称矩阵（symmetric matrix）A等于其转置：A = A^⊤。
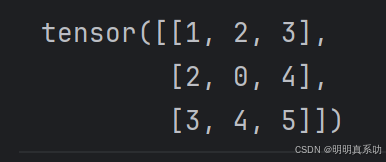
定义⼀个对称矩阵B

B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])

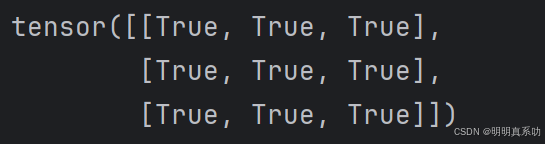
将B与它的转置进⾏⽐较

B == B.T

矩阵是一种非常有用的数据结构，它使我们能够以结构化的方式组织具有不同特征的数据。
例如，在矩阵中，每一行可以代表一个不同的房屋（数据样本），而每一列则对应不同的属性。
尽管，在数学中单个向量默认是列向量，但在表示表格数据集的矩阵中，将每个数据样本作为行向量更为常见。
这种约定将有助于支持常见的深度学习实践。例如，沿着张量的最外层维度，我们可以访问或遍历小批量的数据样本。

1.4 张量

正如向量是标量的推广，矩阵是向量的推广，我们可以构建具有更多维度的数据结构。
张量提供了一种通用的方法来描述具有任意数量维度的n维数组。
例如，向量是一阶张量，矩阵是二阶张量。
张量用特殊的大写字母表示（如X、Y和Z），它们的索引机制（例如x_ijk和[X]_1,2i−1,3）与矩阵的索引类似。

处理图像时，张量将变得更加重要
图像以n维数组形式出现，其中3个轴对应于⾼度、宽度，以及⼀个通道（channel）轴，⽤于表⽰颜⾊通道（红⾊、绿⾊和蓝⾊）

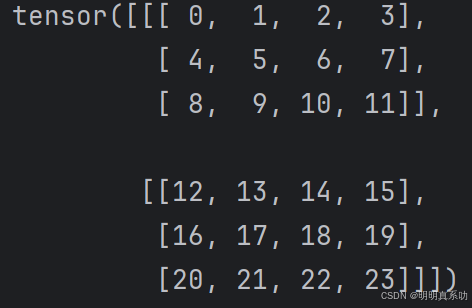
X = torch.arange(24).reshape(2, 3, 4) # reshape(C,H,W)--》（通道数，行数，列数） 

1.4.1 张量算法的基本性质

标量、向量、矩阵以及任意数量维度的张量具有一些实用的属性。
例如，从按元素操作的定义中，我们可以注意到，任何按元素的一元运算都不会改变操作数的形状。同样，给定两个具有相同形状的张量，任何按元素的二元运算结果也将是一个相同形状的张量。
例如，将两个相同形状的矩阵相加时，会对这两个矩阵执行元素级的加法运算（对应位置相互运算）。

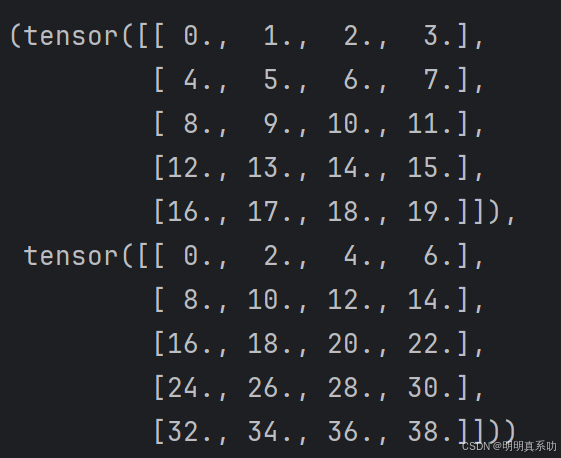
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()
A, A + B

具体⽽⾔，两个矩阵的按元素乘法称为Hadamard积（Hadamard product）（数学符号⊙）。对于矩阵B ∈ R_m×n，其中第i⾏和第j列的元素是b_ij。
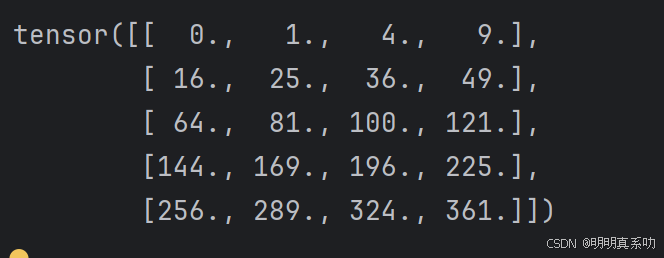
矩阵A和B的Hadamard积为：

A * B

此外！
将张量乘以或加上⼀个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘。

a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape

1.5 降维

我们对任意张量进行的一项有用操作是计算其所有元素的和。
在数学表示法中，我们使用求和符号∑来表示求和。为了表示一个长度为d的向量中所有元素的总和，可以记作
$$\sum _{i=1}^d{x}_i$$

x = torch.arange(4, dtype=torch.float32)
x, x.sum()

我们能够表示任意形状张量的元素总和。
例如，对于矩阵A，其所有元素的和可以表示为:
$$\sum _{i=1}^m\sum _{j=1}^n{a}_{ij}$$

A.shape, A.sum()

当我们使用求和函数时，默认情况下它会将张量的所有元素加起来，最终得到一个单一的数值，也就是标量。
这就像是把一个多维的数据结构压缩成一个点。
如果我们想要在特定的维度上进行求和，比如在矩阵（二维张量）中，我们可以指定沿着某一行或某一列来求和。

1. 以矩阵为例，如果我们想要沿着所有的行（也就是沿着轴0，因为矩阵的第一维是行）来求和，减少一个维度，我们可以告诉求和函数沿着axis=0操作。
   这样，原本矩阵中行的维度就会在结果中消失，我们得到的就是一个包含所有行元素和的向量，这个向量的长度就是矩阵的列数。
   简单来说，就是把每一行的数加起来，得到一个新的一维数组。

A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape

A由5行4列变成了1行4列

2. 指定axis=1将通过汇总所有列的元素降维（轴1）。

A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape

A由5行4列变成了1行5列

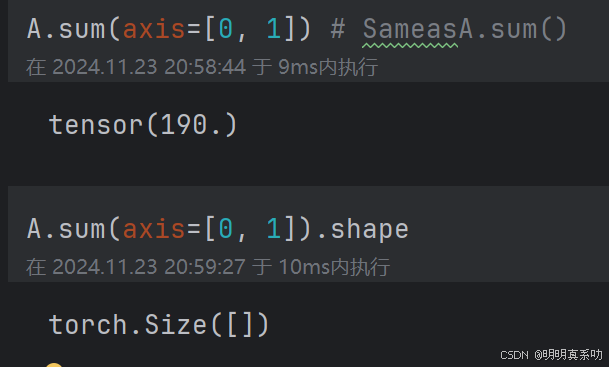
3. 沿着⾏和列对矩阵求和，等价于对矩阵的所有元素进⾏求和

A.sum(axis=[0, 1]) 

变成了标量

⼀个与求和相关的量是平均值（mean或average）。
我们通过将总和除以元素总数来计算平均值。

A.mean(), A.sum() / A.numel()

计算平均值的函数也可以沿指定轴降低张量的维度

A.mean(axis=0), A.sum(axis=0) / A.shape[0]

1.5.1 非降维求和

有时在调⽤函数来计算总和或均值时保持轴数不变会很有⽤。

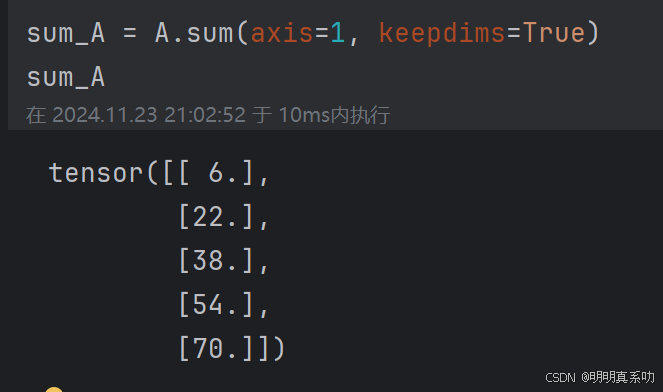
sum_A = A.sum(axis=1, keepdims=True)
sum_A

由于sum_A在对每⾏进⾏求和后仍保持两个轴，我们可以通过⼴播将A除以sum_A

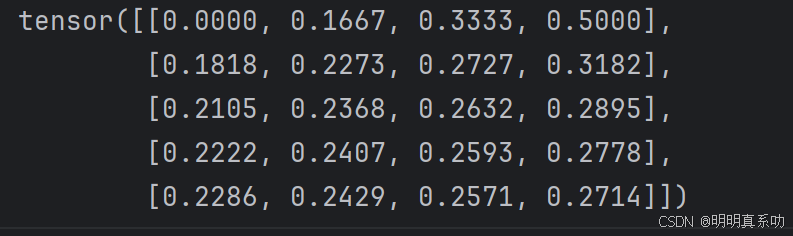
A / sum_A

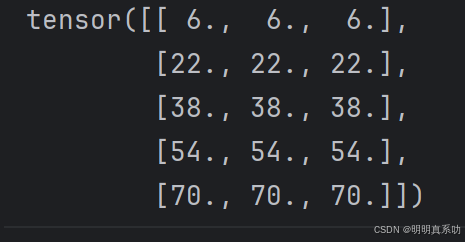
如果我们想沿某个轴计算A元素的累积总和，如axis=0（按⾏计算），我们可以调⽤cumsum函数。
此函数不会沿任何轴降低输⼊张量的维度

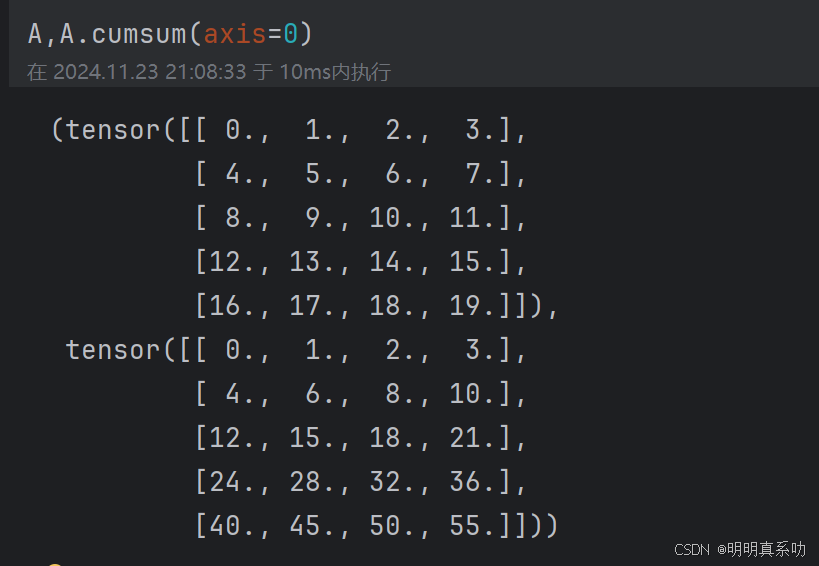
A,A.cumsum(axis=0)

第一行是自身
第二行是第一行+第二行
第三行是第一行+第二行+第三行
…
以此类推

1.6 点积

我们已经学习了按元素操作、求和和计算平均值。另一个基础操作是点积。
给定两个向量x, y ∈ R^d，它们的点积（dot product）x^⊤y （或⟨x, y⟩），是对应位置元素乘积的总和，计算公式为：
$${\mathbf{x}}^{\top }\mathbf{y}=\sum _{i=1}^d{x}_i{y}_i$$

y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)

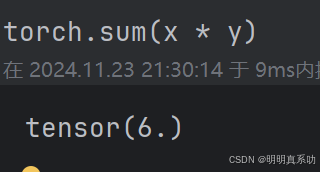
可以通过执⾏按元素乘法，然后进⾏求和来表⽰两个向量的点积:

torch.sum(x * y)

点积在许多应用场景中都非常有用。
例如， $$如果我们有一组由向量\mathbf{x}\in {\mathbb{R}}^d,表示的值$$
$$以及一组由向量\mathbf{w}\in {\mathbb{R}}^d,表示的权重$$
那么 $$\mathbf{x}中的值根据权重\mathbf{w}的加权和可以表示为点积{\mathbf{x}}^{\top }\mathbf{w}$$
$$当权重是非负数且它们的和为1,即\sum _{i=1}^d{w}_i=1时,点积表示加权平均值。$$

将两个向量规范化到单位长度后，点积表示它们之间夹角的余弦值。

1.6.1 矩阵-向量积

现在我们知道如何计算点积，我们可以开始理解矩阵-向量积（matrix-vector product）。

矩阵 $$A\in {\mathbb{R}}^{m\times n}和向量x\in {\mathbb{R}}^n可以这样表示：$$

$$A=\left[\begin{array}{c}{a}_1^{\top }\\ a_2^{\top }\\ ⋮\\ a_m^{\top }\end{array}\right]$$

$$其中每个a_i^{\top }\in {\mathbb{R}}^n是一个行向量，代表矩阵A的第i行。$$

矩阵与向量的乘积 Ax 会产生一个长度为 m 的列向量，其第 i 个元素是行向量 a^T_i与向量 x 的点积：
$$Ax=\left[\begin{array}{c}{a}_1^{\top }\\ a_2^{\top }\\ ⋮\\ a_m^{\top }\end{array}\right]x=\left[\begin{array}{c}{a}_1^{\top }x\\ a_2^{\top }x\\ ⋮\\ a_m^{\top }x\end{array}\right]$$

$$我们可以将矩阵A\in {\mathbb{R}}^{m\times n}的乘法视为一种从{\mathbb{R}}^n到{\mathbb{R}}^m的向量转换。$$
这种转换在许多情况下都非常有用，比如在表示旋转时，我们可以使用方阵的乘法。

我们可以使用张量来表示矩阵-向量积，并且使用与点积相同的 mv 函数来实现。
当我们调用 torch.mv(A, x) 时，将执行矩阵-向量积运算。这里需要注意的是，矩阵 A 的列数（即沿轴1的长度）必须与向量 x 的长度相匹配。

A.shape, x.shape, torch.mv(A, x)

1.6.2 矩阵-矩阵乘法

原理同上，我们可以将矩阵-矩阵乘法AB看作是简单地执⾏m次矩阵-向量积，并将结果拼接在⼀起，形成⼀个n × m矩阵。
在下⾯的代码中，我们在A和B上执⾏矩阵乘法。这⾥的A是⼀个5⾏4列的矩阵，B是⼀个4⾏3列的矩阵。两者相乘后，我们得到了⼀个5⾏3列的矩阵。

B = torch.ones(4, 3)
torch.mm(A, B)

1.7 范数

在数学的线性代数领域，范数是一种非常实用的工具，它用来衡量向量“大小”的一种方式。这里的“大小”并不是指向量在空间中占据的体积，而是指向量各分量数值的总体“规模”。

范数是一个函数，它接受一个向量作为输入，并输出一个标量（一个单独的数值），这个数值告诉我们向量的大小。向量的范数需要满足几个关键属性：

1. 缩放不变性：如果你将向量的所有元素乘以一个常数α，那么向量的范数也会乘以α的绝对值。这就像是你将一个物体的所有尺寸都放大或缩小相同的比例，它总体的大小也会按相同的比例变化。
   $$f(\alpha x)=|\alpha |f(x)$$

2. 三角不等式：这个性质告诉我们，两个向量的范数之和总是大于或等于这两个向量相加后的范数。这类似于在平面上，两点之间的直线距离总是小于或等于这两点分别到第三点的距离之和。
   $$f(x+y)\le f(x)+f(y)$$

3. 非负性：范数总是非负的，因为大小是一个非负的概念。在数学上，这意味着向量的范数永远不会是负数。
   $$f(x)\ge 0$$

4. 零向量：如果一个向量的所有元素都是0，那么它的范数也是0。这很直观，因为一个所有分量都是0的向量在几何上就是一个点，没有“大小”。
   $$\forall i,[x]i=0\iff f(x)=0.$$

5. 范数的概念与我们熟知的欧几里得距离（直线距离）相似。
   例如，如果你在二维空间中有一个点，其坐标为(x, y)，那么这个点到原点的距离就是√(x² + y²)，这是根据毕达哥拉斯定理得出的。在数学中，这被称为L2范数，它是向量所有元素平方和的平方根。
   $$\Vert \mathbf{x}{\Vert }_2=\sqrt{\sum _{i=1}^n{x}_i^2}$$
   其中，在L2范数中常常省略下标2，也就是说∥x∥等同于∥x∥₂。
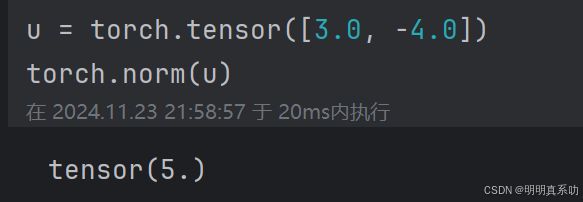
   在代码中，我们可以按如下⽅式计算向量的L2范数:

u = torch.tensor([3.0, -4.0])
torch.norm(u)

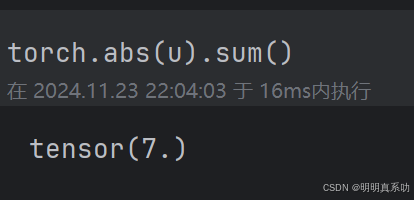
在深度学习中，我们更经常地使⽤L2范数的平⽅。你还会经常遇到L1范数，它表⽰为向量元素的绝对值之和：
$$\Vert \mathbf{x}{\Vert }_1=\sum _{i=1}^n\left|x_i\right|$$

torch.abs(u).sum()

L2范数和L1范数都是更⼀般的Lp范数的特例：
$$\Vert \mathbf{x}{\Vert }_p={\left(\sum _{i=1}^n{\left|x_i\right|}^p\right)}^{1/p}$$
类似于向量的L2范数，矩阵X ∈ R^m×n的Frobenius范数（Frobenius norm）是矩阵元素平⽅和的平⽅根：
$$\Vert \mathbf{X}{\Vert }_F=\sqrt{\sum _{i=1}^m\sum _{j=1}^n{x}_{ij}^2}$$
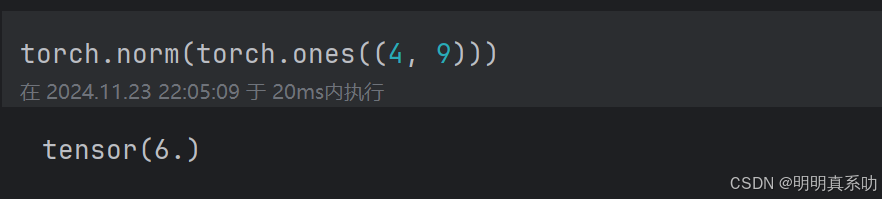
Frobenius范数满⾜向量范数的所有性质，它就像是矩阵形向量的L2范数。调⽤以下函数将计算矩阵
的Frobenius范数。

torch.norm(torch.ones((4, 9)))

在深度学习领域，我们经常致力于解决各种优化问题，这些问题的核心目标可以是：
6. 最大化观测数据的概率：这意味着我们试图找到模型参数，使得模型能够以最高的概率生成或预测观测到的数据。
7. 最小化预测与真实观测之间的距离：这通常涉及到损失函数，它衡量模型预测值与实际值之间的差异，我们的目标是最小化这个差异。
此外，我们经常使用向量来表示不同的物品，如单词、产品或新闻文章。这样做的目的是为了在向量

空间中：

• 最小化相似项之间的距离：相似的物品在向量空间中应该更接近，这有助于捕捉它们之间的相似性。
• 最大化不同项之间的距离：不同的物品在向量空间中应该更远离，这有助于区分它们之间的差异。
  在深度学习中，目标函数（或损失函数）是算法的心脏，它定义了我们希望通过训练过程优化的内容。除了数据之外，目标函数可能是深度学习算法最重要的组成部分。它通常被表达为一个范数，这是一种衡量向量大小或长度的方法，用于量化模型预测与实际观测之间的差异。通过最小化这个范数，我们可以训练模型以提高其预测的准确性。

总结

在本周的学习中，由于下周考试和课程论文的压力，我的学习进度有所放缓。
通过本文，我深入理解了深度学习中线性代数的重要性，并掌握了标量、向量、矩阵和张量的基本操作。我还学习了如何通过降维技术来处理和分析数据。考试结束后，我计划加快学习进度，并将所学知识应用于深度学习模型的构建和优化，以便更深入地理解和实践深度学习技术。
下一周计划把微分的代码底层原理用代码过一遍，然后继续复习原来学习的内容。