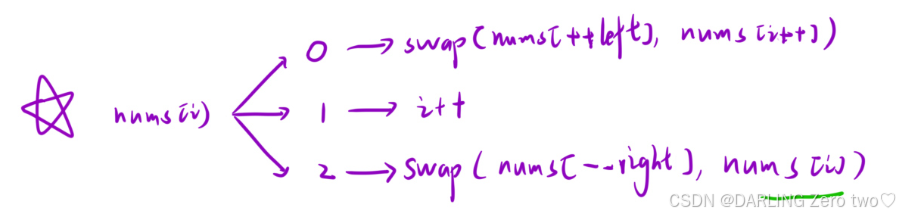本篇是优选算法之分治-快排,快排可以在更短的时间内完成相同规模数据的排序任务,大大提升了运算效率,空间复杂度在平均状况下仅为O(log N)
1.概念解析
🚩什么是分治-快排?
分治是核心思想,即将大问题拆解成形式相同的小问题来处理,从待排序数组里挑出一个元素当作基准,设置两个指针,一个从数组开头,一个从末尾出发,先把一个无序的数组划分成两个子数组,接着分别处理这两个子数组,随着递归深入,子数组越来越小,最终每个子数组只剩 1 个元素时,天然有序,整个大数组也就完成排序
2.颜色分类
✏️题目描述:
✏️示例:
传送门:颜色分类
题解:
对于排序的题目,根据前些的学习我们一般都是想到冒泡排序等基础算法,但是此类算法对于带有重复性的排序很不友好,还是太慢了,因此对于这道题,也是一道经典的荷兰国旗问题,使用类似双指针算法中的移动零那道题的方法,划分区间比较排序,衍生出来了一种三划分排序算法,也叫作快速排序
💻第一步:
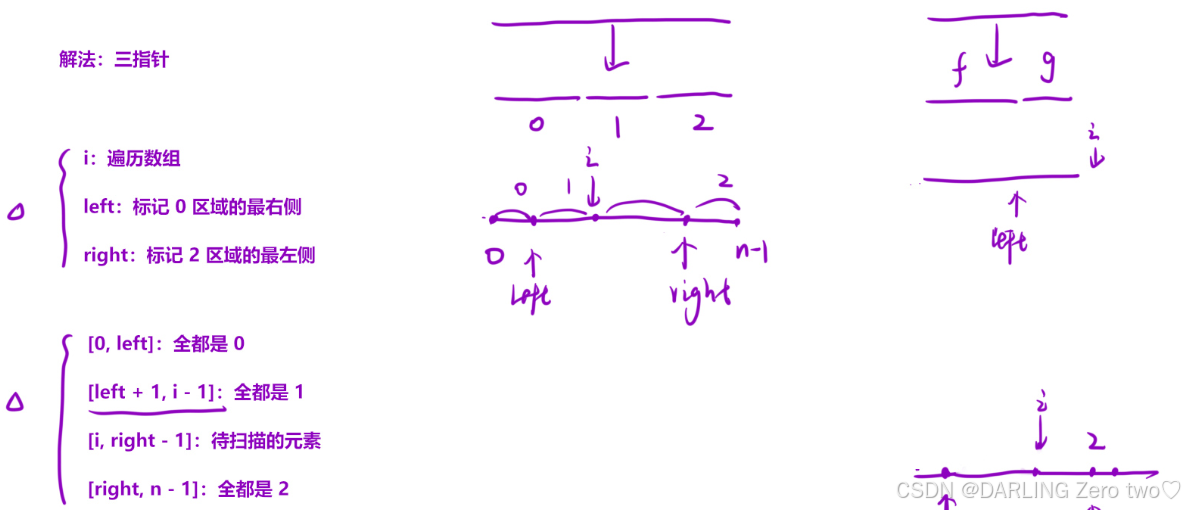
首先我们这题要排序的是0、1、2三个数字,所以划分为三个区间,分别是小于1的区间,等于1的区间,大于1的区间。left表示标记左区间的指针,i表示扫描区间指针,right表示标记右区间的指针
💻第二步:
前提条件left = -1, right = n,根据i扫描的区间,可以分为三种情况:如果遇到0,要放在左区间,left先++,和i所指的元素互换,然后i++扫描下一个元素;如果遇到1,本来就要放在中间区间,所以不用操作,i++扫描下一个元素;如果遇到2,要放在右区间,right先--,和i所指的元素互换,注意i不能++,因为此时交换过来的元素还没扫描过,要再判断一次。right和i相遇时停止扫描
💻代码实现:
#include <iostream>
#include <vector>
using namespace std;
class Solution
{
public:
void sortColors(vector<int>& nums)
{
int n = nums.size();
int left = -1, right = n, i = 0;
while (i < right)
{
if (nums[i] == 0)
{
swap(nums[++left], nums[i++]);
}
else if(nums[i] == 2)
{
swap(nums[--right], nums[i]);
}
else
{
i++;
}
}
}
};
3.排序数组
✏️题目描述:
✏️示例:
传送门:排序数组
题解:
本题其实和三色划分的道理是相同的,只不过该题才是真正的将快速排序的方法效率最大化,能普及到大部分的题目上,重点是要选取基准元素划分区间
💻第一步:
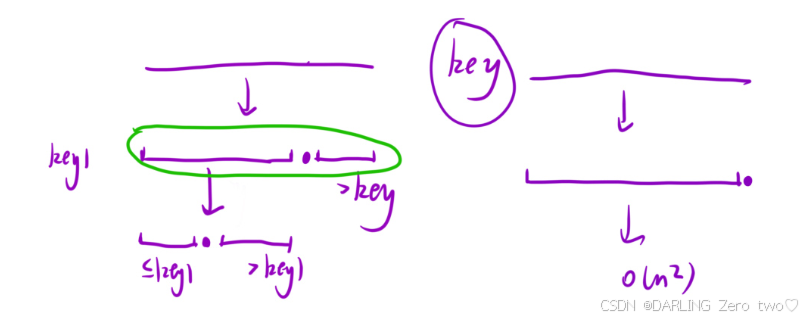
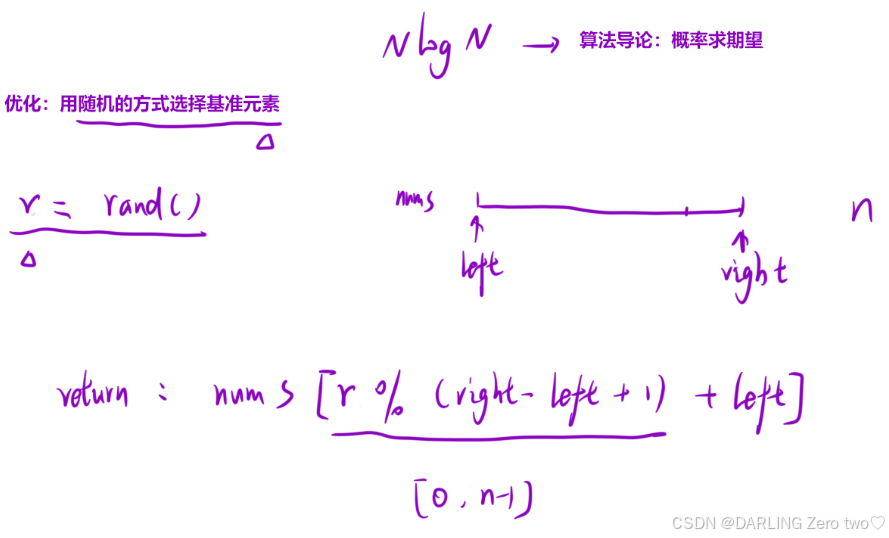
根据算法导论的期望严谨证明,发现用随机的方式选取基准元素是最优的算法,因此我们可以使用rand()随机函数,最开始调用qsort时,此时计算随机数的范围就是基于 [l, r] 这个初始区间,left作为基准偏移,让随机选取的索引能落在这个完整初始区间内
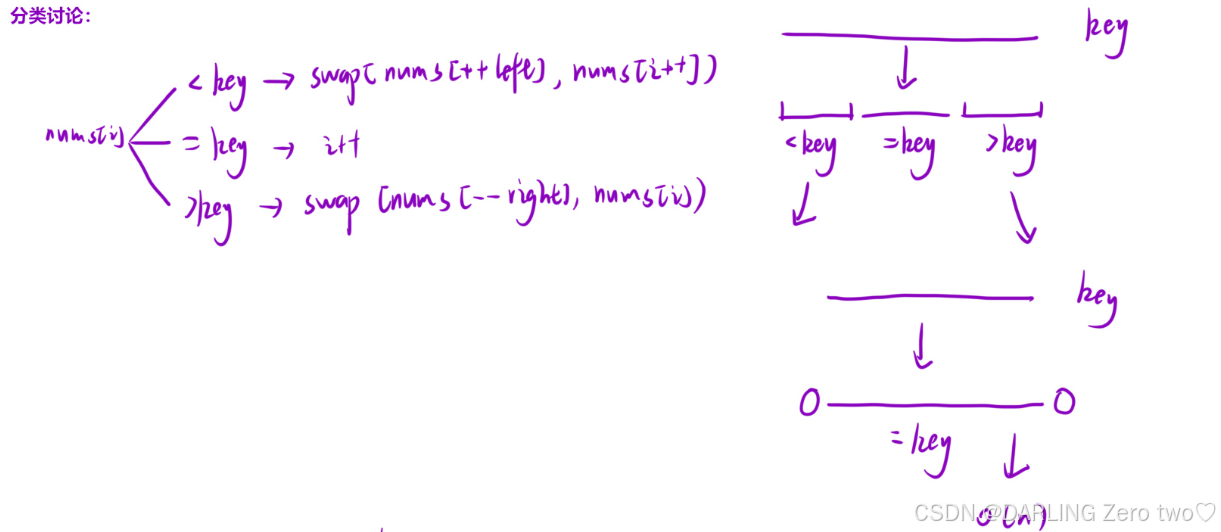
💻第二步:
既然已经选取完基准元素,那么划分的过程和三色划分是一样的,此时要注意,第一轮划分完后,left在基准元素左边一位,right在基准元素右边一位,此时就完成了两个字区间的划分,但是左右两个区间只是大于或小于,区间内的数据排序还是乱的,所以还要对左右两个区间进行相同的排序,依次往复,每次排序都能确定一个基准元素的位置
💻代码实现:
#include <iostream>
#include <vector>
#include <ctime>
using namespace std;
class Solution {
public:
vector<int> sortArray(vector<int>& nums)
{
srand(time(NULL));
qsort(nums, 0, nums.size() - 1);
return nums;
}
void qsort(vector<int>& nums, int l, int r)
{
if (l >= r)
return;
int key = getRandom(nums, l, r);
int i = l, left = l - 1, right = r + 1;
while (i < right)
{
if (nums[i] < key)
{
swap(nums[++left], nums[i++]);
}
else if (nums[i] > key)
{
swap(nums[--right], nums[i]);
}
else
{
i++;
}
}
qsort(nums, l, left);
qsort(nums, right, r);
}
int getRandom(vector<int>& nums, int left, int right)
{
int r = rand();
return nums[r % (right - left + 1) + left];
}
};
4.数组中的第k个最大元素
✏️题目描述:
✏️示例:
传送门:数组中的第k个最大元素
题解:
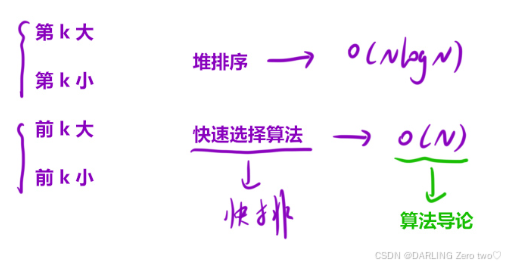
本题要求找数组中的第k个最大元素,本质是快速排序算法中的快速选择算法,该方法同样适用第k小,前k大,前k小
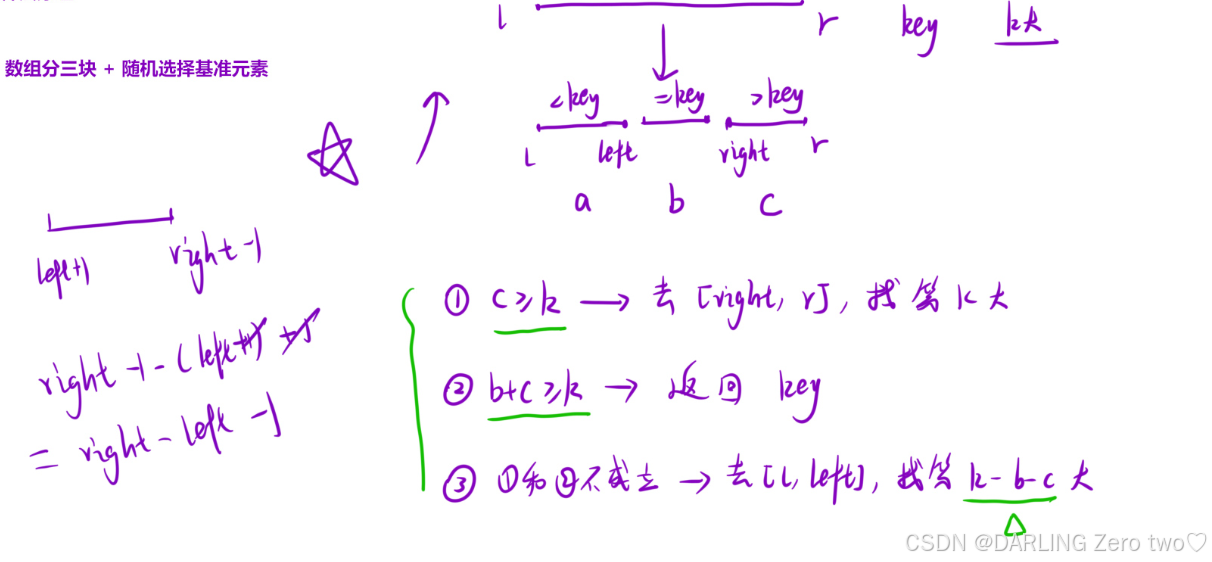
💻细节问题:
快速选择算法和快速排序基本上一样,唯一不同的是要在递归时选择区间,若c>=k,说明第k大落在大于基准元素的这段区间,那么只在这段区间寻找即可;若b+c>=k,说明第k大就在等于基准元素这段区间,即等于基准元素;若前面两种都不成立,那么第k大一定落在比基准元素小的区间,因此在整个区间上找第k大相当于在左区间上找第k-b-c大
💻代码实现:
#include <iostream>
#include <vector>
#include <ctime>
using namespace std;
class Solution
{
public:
int findKthLargest(vector<int>& nums, int k)
{
srand(time(NULL));
return qsort(nums, 0, nums.size() - 1, k);
}
int qsort(vector<int> nums, int l, int r, int k)
{
if (l == r) return nums[l];
int key = getRandom(nums, l, r);
int left = l - 1, right = r + 1, i = l;
while (i < right)
{
if (nums[i] < key)
{
swap(nums[++left], nums[i++]);
}
else if (nums[i] > key)
{
swap(nums[--right], nums[i]);
}
else
{
i++;
}
}
int c = r - right + 1, b = right - left - 1;
if (c >= k)
{
return qsort(nums, right, r, k);
}
else if (c + b >= k)
{
return key;
}
else
{
return qsort(nums, l, left, k - b - c);
}
}
int getRandom(vector<int> nums, int left, int right)
{
int r = rand();
return nums[r % (right - left + 1) + left];
}
};
5.库存管理Ⅲ
✏️题目描述:
✏️示例:
传送门:库存管理Ⅲ
题解:
这题其实也是一样的,要求一个区间内的数,只要
求第k个数的位置,然后计算这个区间间的长度就行了
💻代码实现:
#include <iostream>
#include <vector>
#include <ctime>
using namespace std;
class Solution
{
public:
vector<int> inventoryManagement(vector<int>& stock, int cnt)
{
srand(time(NULL));
qsort(stock, 0, stock.size() - 1, cnt);
return { stock.begin(),stock.begin() + cnt };
}
void qsort(vector<int>& stock, int l, int r, int cnt)
{
if (l >= r) return;
int key = getRandom(stock, l, r);
int left = l - 1, right = r + 1, i = l;
while (i < right)
{
if (stock[i] < key)
{
swap(stock[++left], stock[i++]);
}
else if (stock[i] > key)
{
swap(stock[--right], stock[i]);
}
else
{
i++;
}
}
int a = left - l + 1, b = right - left - 1;
if (a > cnt)
{
return qsort(stock, l, left, cnt);
}
else if (a + b >= cnt)
{
return;
}
else
{
return qsort(stock, right, r, cnt - b - a);
}
}
int getRandom(vector<int>& stock, int l, int r)
{
return stock[rand() % (r - l + 1) + l];
}
};