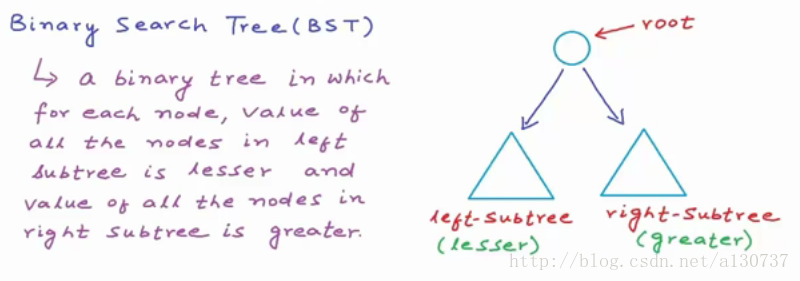
BST, 是一种完备二叉树。 顾名思义, binary search + tree, 可以实现二分查找法, 十分的高效。 BST 又被称为sorted binary tree。 是树的树结构中一种重要的数据结构。 对于每一个节点, 满足这个节点的所有左子树的各个节点的data 均小于(或者等于, 等于其实不太重要, 可以放在右子树部分)这个节点的数据, 右子树的所有节点的数据均大于这个节点的数据。
BST与其他数据结构相比, 主要的优点是与BST相关的排序算法和搜索算法(例如in-order traversal) 非常的高效。 除此之外, 还有如下优点:
(1)当BST是平衡的时候, 插入节点和删除节点的操作很快。
(2)代码简单, 容易实现。
(3)树中的节点是dynamic in nature(可以快速更新BST树, 易于修改)。
对于我们需要存储常常需要modifiable 的数据, BST的有事非常明显。 对于这种modifiable 的数据, 我们常常需要执行如下的基本操作:
下面对这种数据, 我们分析一下采用不同的数据结构, 各大基本操作的时间复杂度。
(1) 选择Array 的数据结构实现对数据的存储:
删除操作:
对于插入操作, 当我们的数组满了的时候, 我们需要申请一个更大的数组(通常2倍与原数组), 然后将数据复制到新的数组中, 此时该插入操作的时间复杂度会高达O(n)。
(2) 使用链表(例如linked list of integers)的时候:
NOTE: 下图中, 我们的插入操作是插在链表头中(故而时间复杂度为O(1), 如果插在尾部, 需要O(n)了), 删除节点需要先搜索, 故而为O(n):
不难看出, 采用上述的数据结构, 搜索某个元素花费的时间很多, 基本上需要很多次比较。我们已经知道, 如果我们在数组中存放着的是已经排好序的元素, 当我们需要查找某一个元素的时候, 可以采用binary search, 从而可以快速的找到数据。
此时时间复杂度为O(logn).
然而, 尽管查找的时间复杂度下降了(对于sorted Array, 查找只需要比较logn 次。), 但是插入和删除的时间复杂度却没有得到改善:
如何避免呢。 答案是采用BST(注意, 为了避免最坏的情况发生, 需要保证我们的BST是平衡的), 将上述三种基本操作的平均时间复杂度降至O(logn)。
下面对BST做简单介绍:
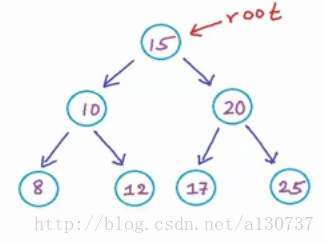
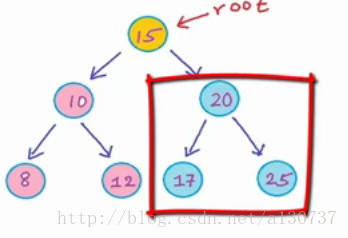
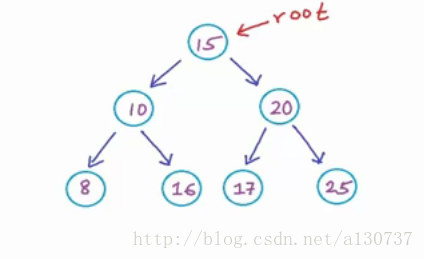
首先BST(注意树的这种递归的数据结构)如下图:
Q:判读下图是否为BST
A:(1)需要对每个节点进行分析:
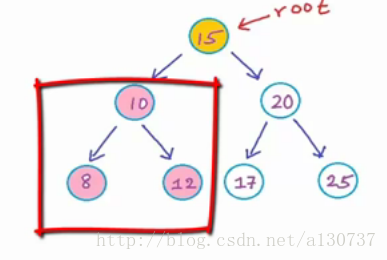
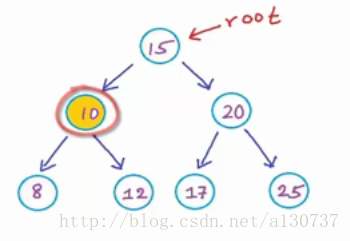
首先对于根节点15:
该节点左子树的所有节点均小于15, 右子树的所有节点均大于15, 所以满足, good node。
对于节点10, 同样的判断方式, 也是一个good node:
同理对于data 为20 的节点, 同样判断, 也是一个good node.
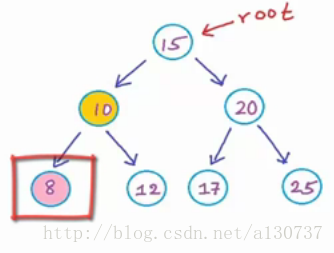
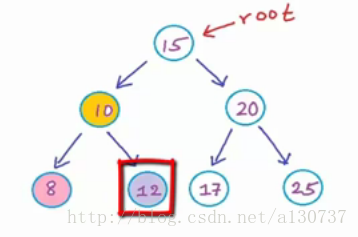
最后剩下叶子节点。 没有子树了, 停止。
所以上述的二叉树是一个BST。
Q1: 下图是一个BST吗
A: 不是的。 因为16 在15的左子树的节点, 但是大于15, 所以这个数不是一个BST。
为什么BST能够加快搜索的速度呢。
首先这源于二分法。 我们已经对对我们的数据排好序。 对于所有空间为n(数据项个数), 通过比较二分, 缩小我们的搜索空间大小, 最终实现准确定位:
使用BST的数据结构的时候, 搜索的操作和(用数组实现的)二分法是相似的。
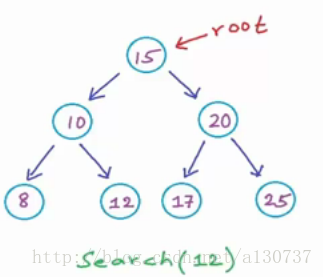
例如下面的BST数据结构:
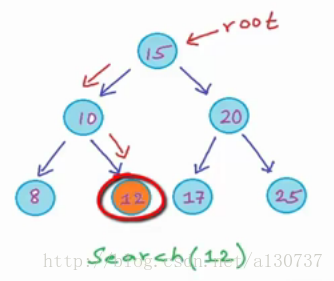
例如, 我们需要查找元素12.。 那么我们从根节点开始, 与根节点的数据(15)相比较, 由于比15小, 我们和左子树的根节点比较(数据为10), 由于12> 10, 向右子树走, 最终找到数据项12 的位置。 不难看出每一次决策在那个子树的时候, 其实就是在二分法(对于平衡的BST)。
设想一下, 如果我们的BST不是平衡的, 那么搜索的时间复杂度就是O(n)了, 并没有得到改善:
对于插入操作, 我们的第一步就是搜索确定被插入数据应该插在那个位置, 以便我们得到的二叉树任然是一个BST。
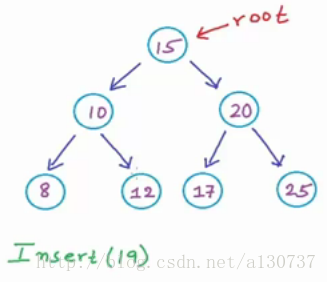
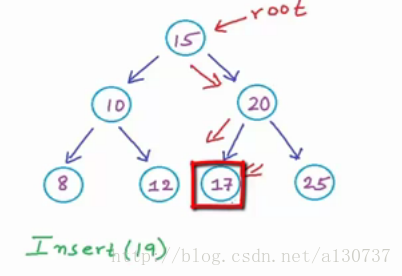
例如下例, 将19 插入到BST中:
首先, 从跟节点开始, 由于19大于15, 所以我们go right, 到达20, 由于19 < 20, 所以go right, 到达17, 17 < 19, 而且17没有右孩子,
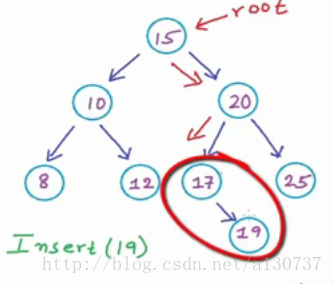
所以我们插在17 的右边, 创建一个数据为19 的node, link 起来, 作为其右孩子:
不难看出, 插入操作的时间复杂度也为O(logn)。
对于删除某个数据的操作, 我们的第一步也是搜索。 然后对link 进行调整。 一般而言, 时间复杂度也是O(logn)。
但是需要指出的是, 插入和删除操作可能会使得我们的BST不再是平衡的了。 所以一般在插入和删除操作完成之后, 我们常常需要做一些操作, 以便恢复BST的平衡性。