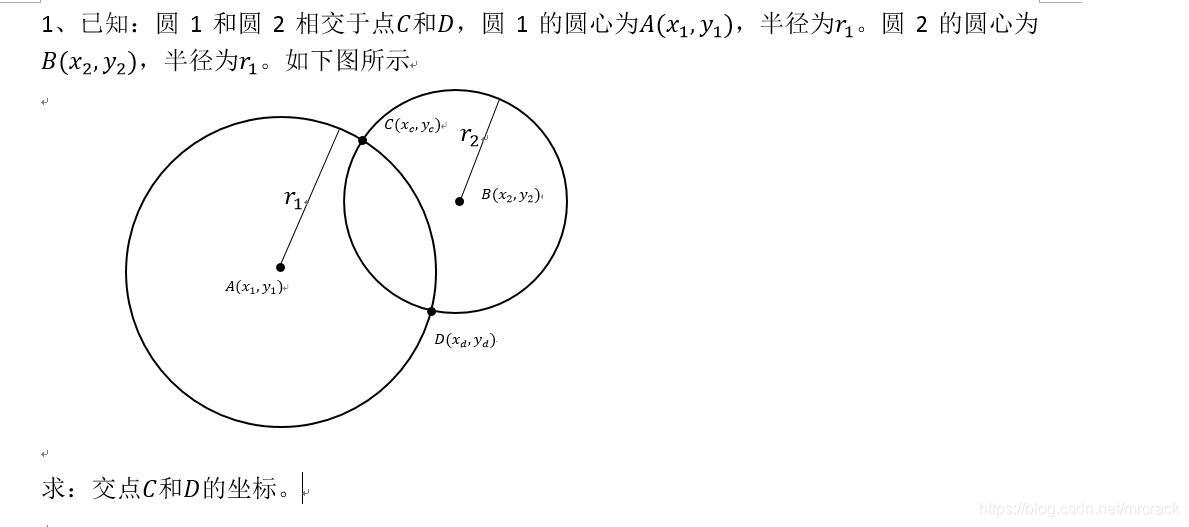
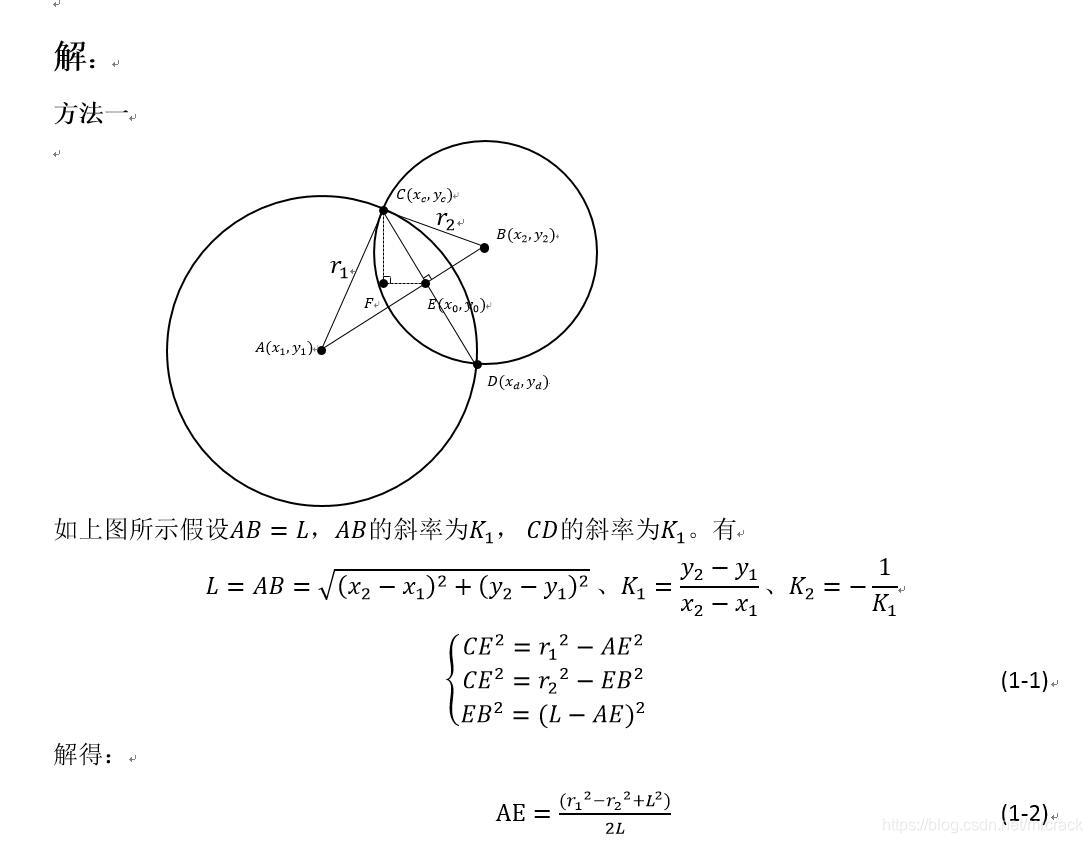
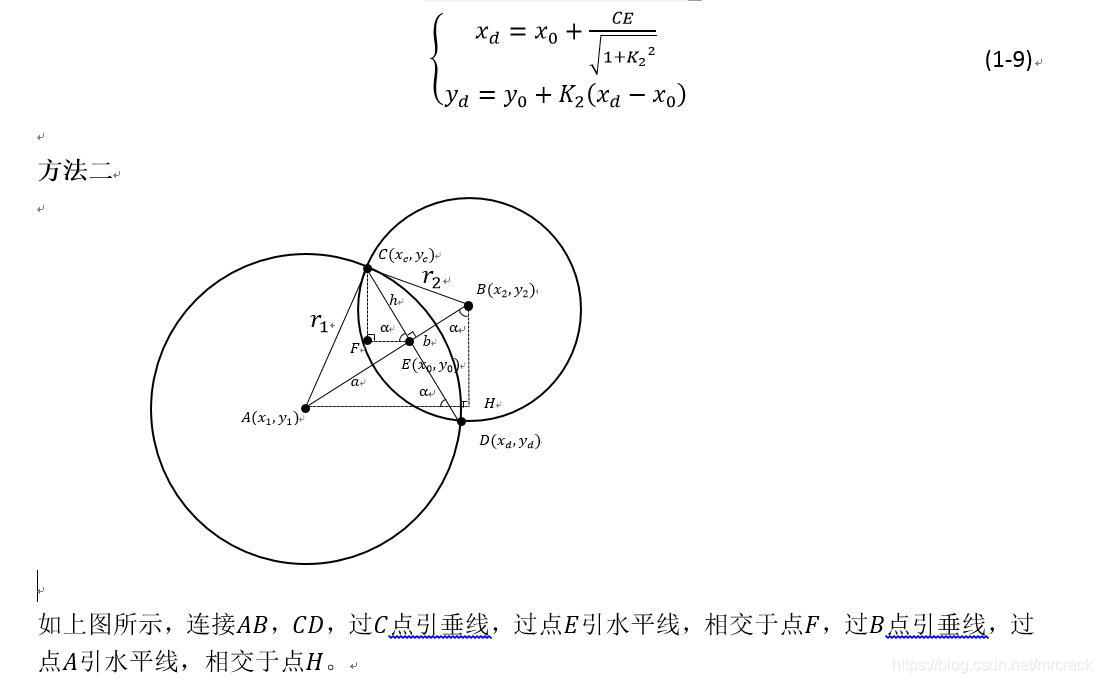
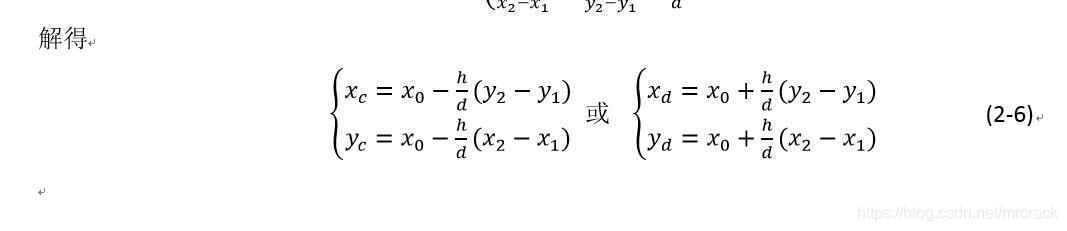摘自https://blog.csdn.net/zx3517288/article/details/53326420
方法一仔细检查了,公式没啥问题,但在实践使用时发现当y1,y2相等时,k2是求不出来的,特殊情况没考虑,建议把最后求y的式子用圆的方程联立
问:大佬们,方法一的CF=EF*K2怎么得到的呀,看不懂啊
答:
1.CF是垂直x轴,EF与x轴平行。∠FEC 为斜边与x轴正方向的夹角,再根据直线斜率定义,放到直接三角形里,斜率k为对边 / 邻边(k = CF / EF)。斜率是可以为负的。更严谨写法为 CF = EF * | K2|,
2.懂了,感谢
3.他上边写错了 因该是斜率k1和k2,,他怼成一样了
问:方法二凭空而来的两个三角形相似
答:
因为角FEC和角ABH相等,两个三角形都有直角,所以两个三角形的三个内角对应相等
问:为什么不用简单方法呢, (x-x₁)²+(y-y₁)²=r₁² (x-x₂)²+(y-y₂)²=r₂²
答:请问你是联立解方程吗,那个好像也很麻烦
下面的推导中,两三角形相似符号,错写成全等符号
yc,yd最后公式有误,应为
yc=y0+h*(x2-x1)/d
yd=y0-h*(x2-x1)/d
xd,yd求法与xc,yc求法雷同,构造一个与CFE全等的三角形,图中未画出。注意E是CD的中点,这一点根据图形的对称性可得。