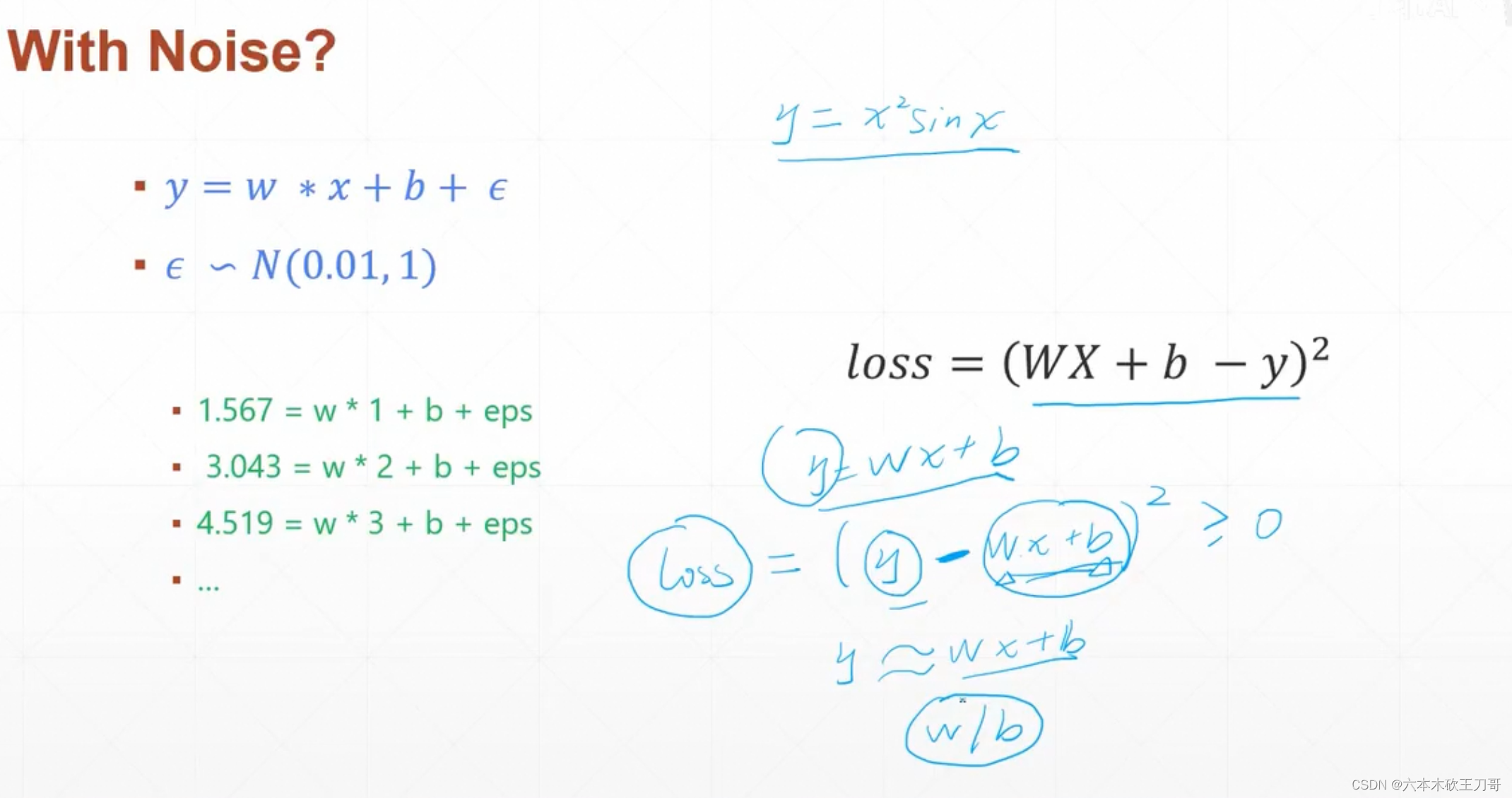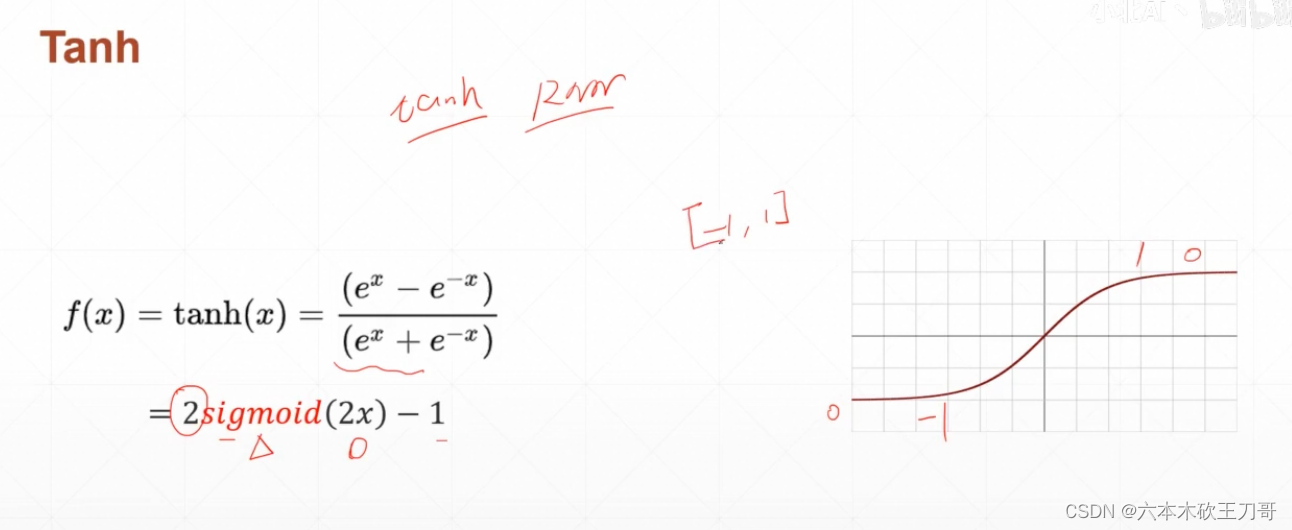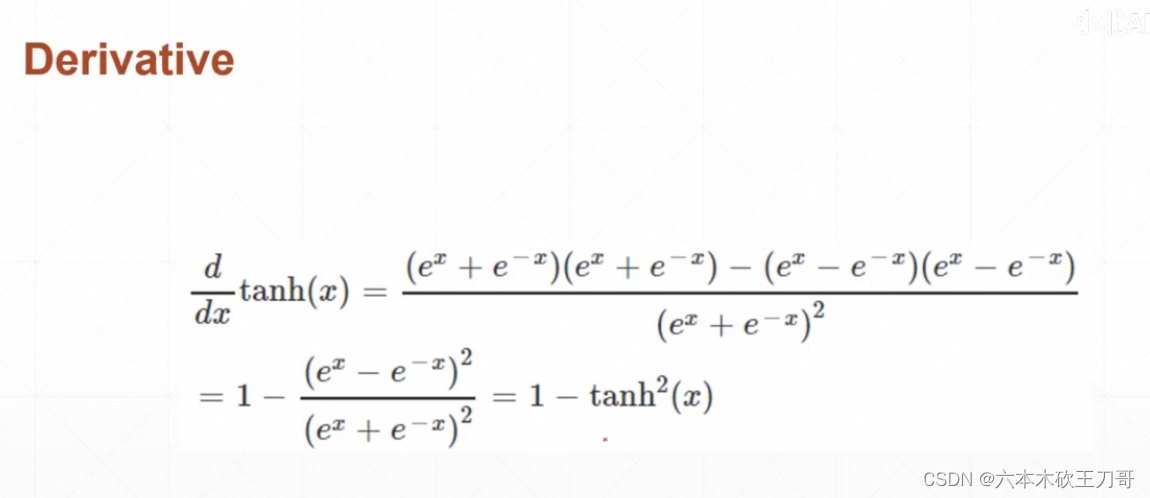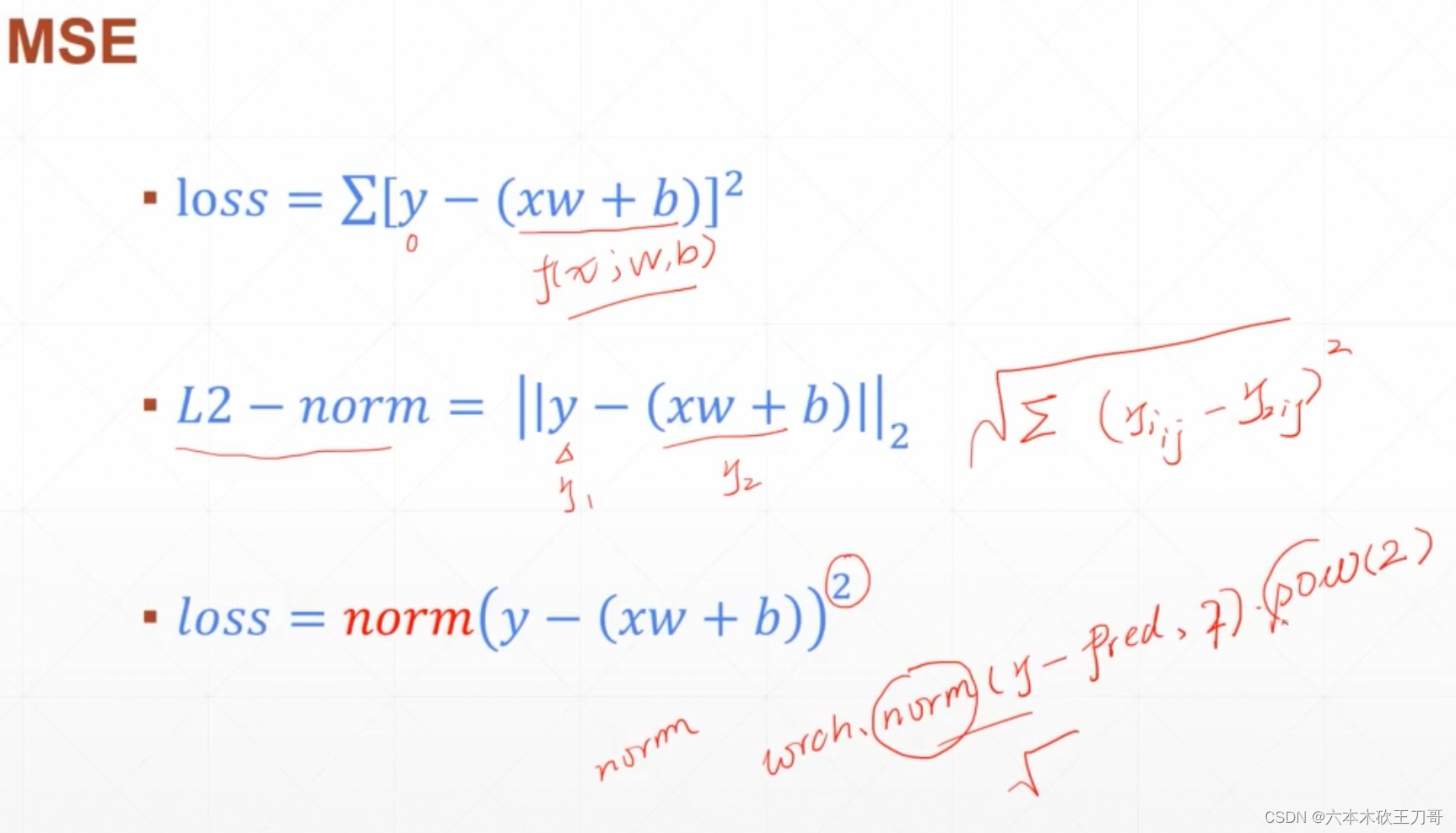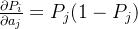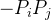1.梯度下降和线性回归

来源：PyTorch深度学习框架【龙良曲】

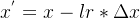
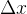
机器学习的精髓在于梯度下降，梯度下降的公式就是，其中就是Loss对x求偏导，当然这里x的意思是某个参数，所以对于和Loss相关的任意参数都可以对其求导。

下图中第一个图是设置了相对较小的学习率lr，所以每次往下走的速度较慢，但是第二幅图学习率较大，导致找最小值的过程会来回跳跃，比如说某次从最小值5的左边开始，负梯度过大的时候会跳跃到5的右边，这时候梯度变成正梯度，会导致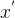又回到5的左边，直到最后收敛。

在简单的数学中求解线性方程组，给出两个样本点就可以解出完整的方程形式，但是在现实很多情况下需要近似计算，例如可能会给出1000个样本，如果我们需要用线性方程去近似，就需要保证误差在一定范围内，这时候可以列出损失函数来进行梯度下降，找出最合适的参数w和b。

问题实战：

MNIST手写数字识别问题

2.数据类型

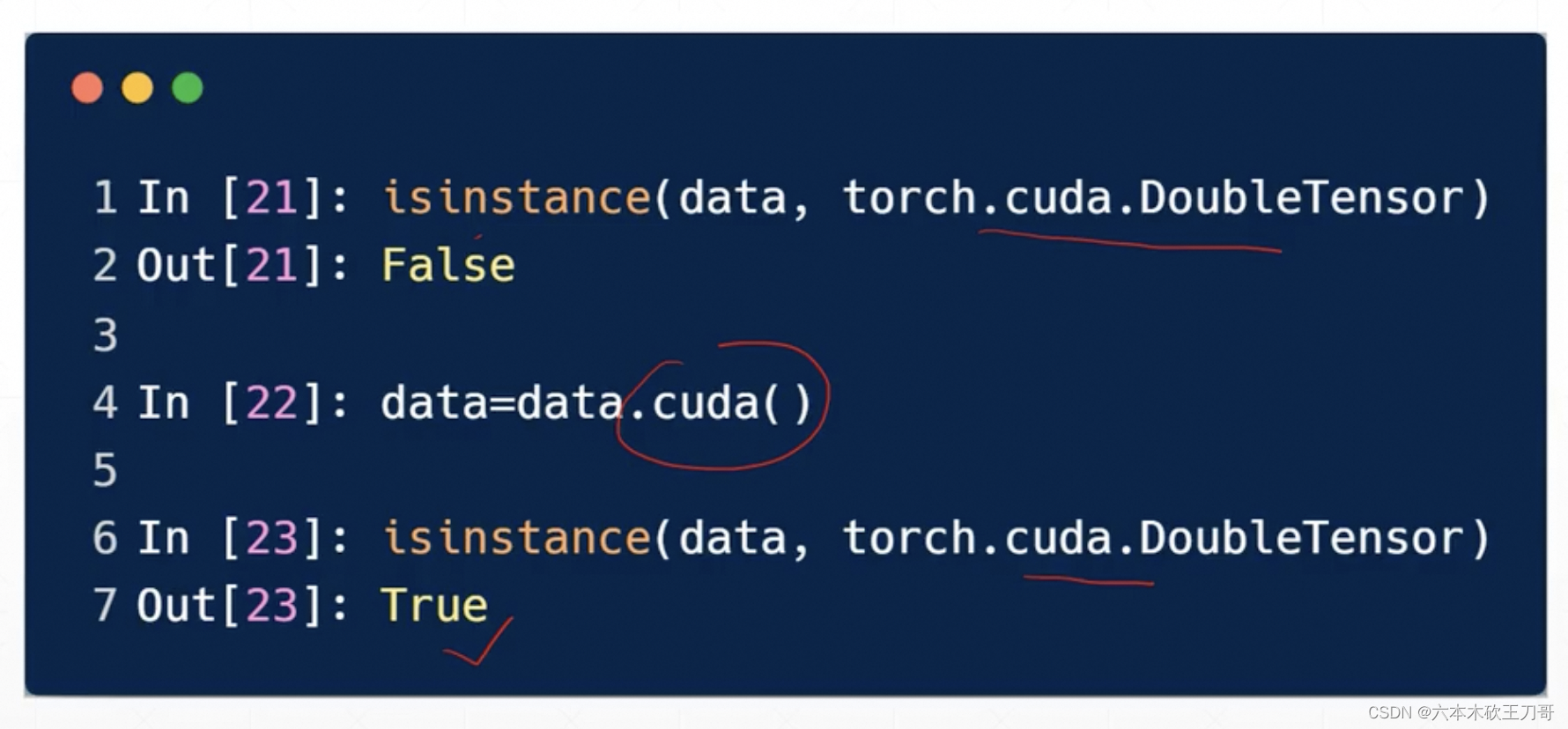
在CPU和GPU上类型是不一样的，可以使用.cuda来修改类型

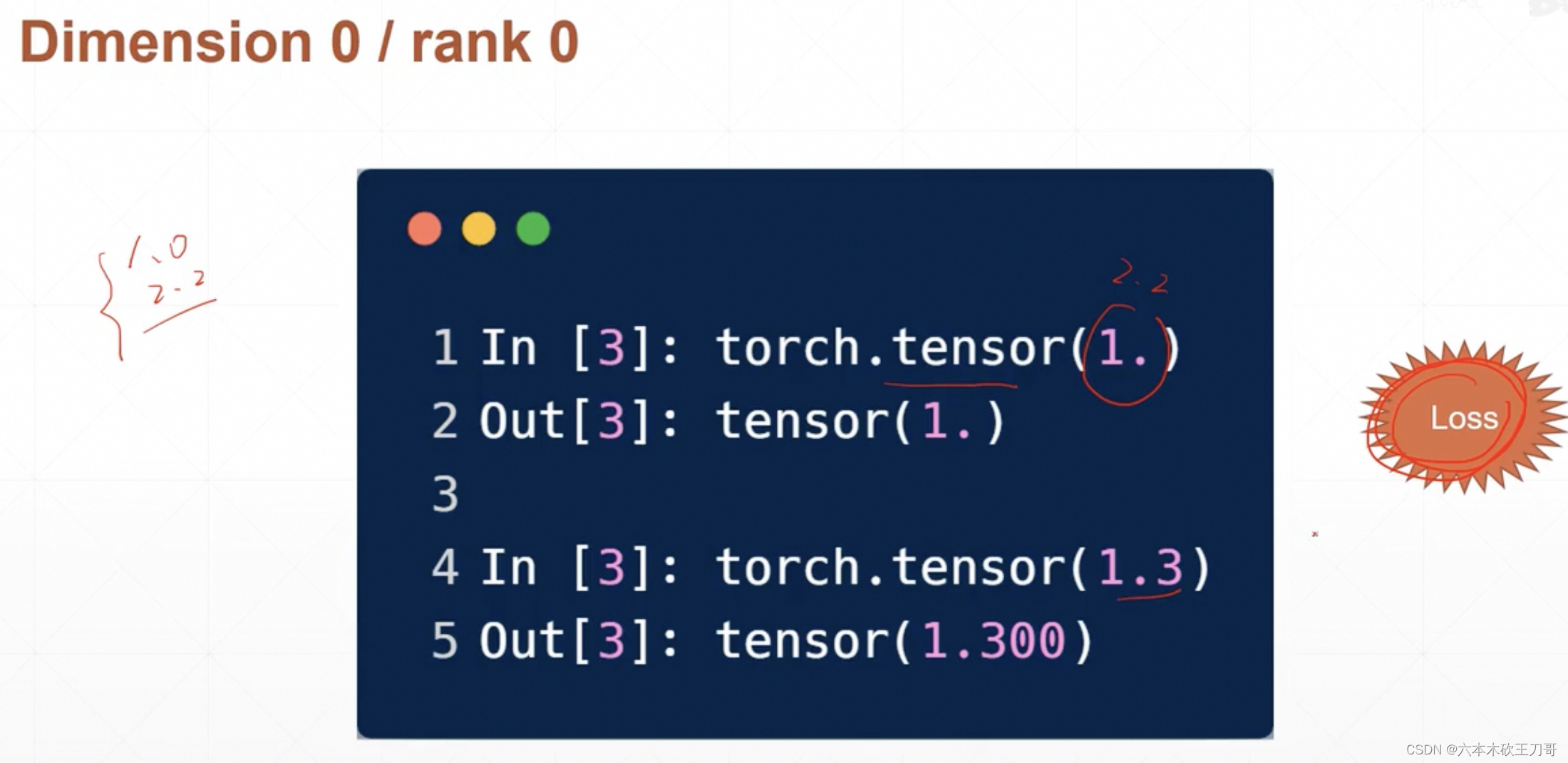
Dimension为0的Tensor类型的主要作用是计算Loss

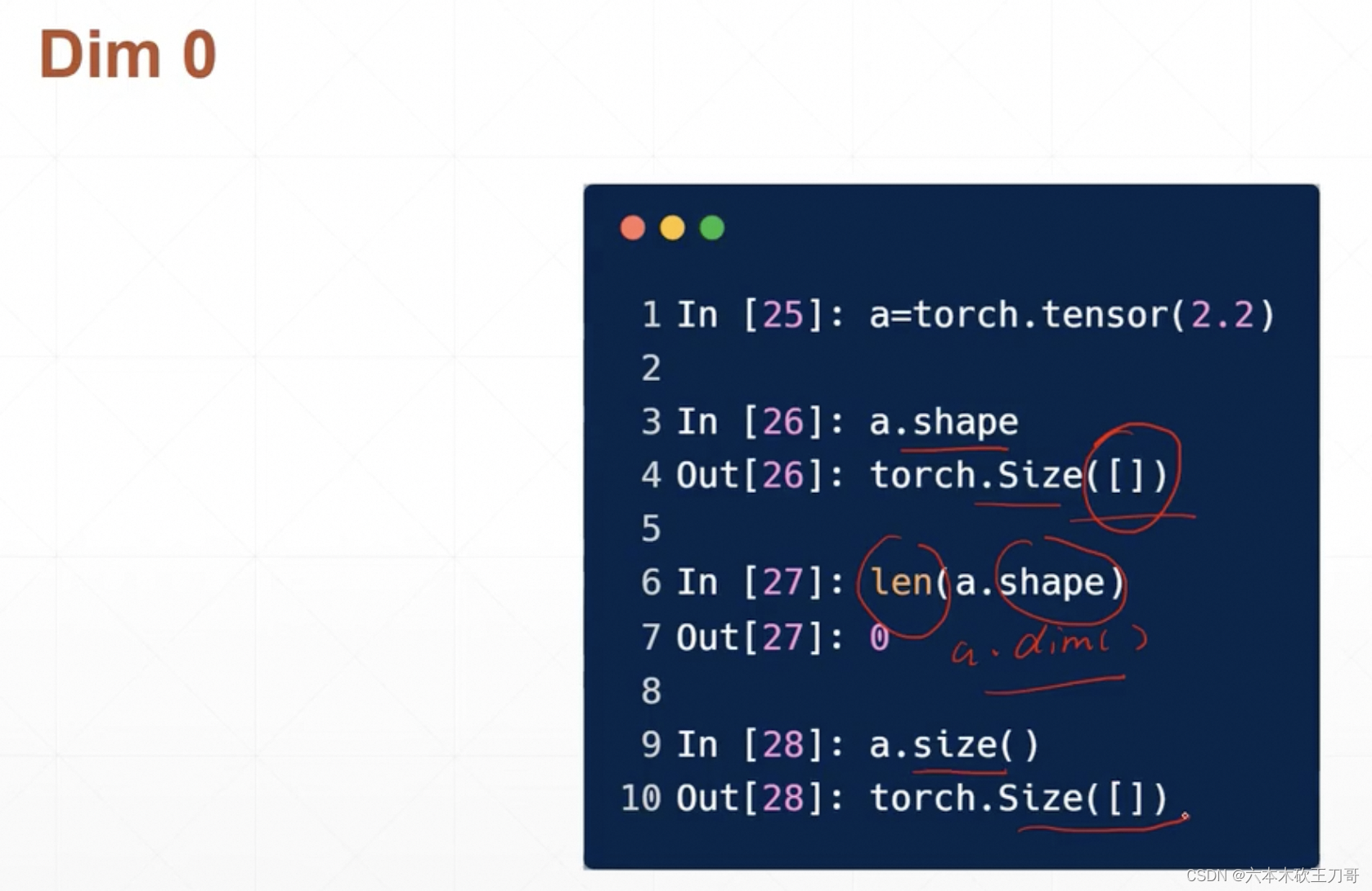
 Dim为0的标量的一些方法

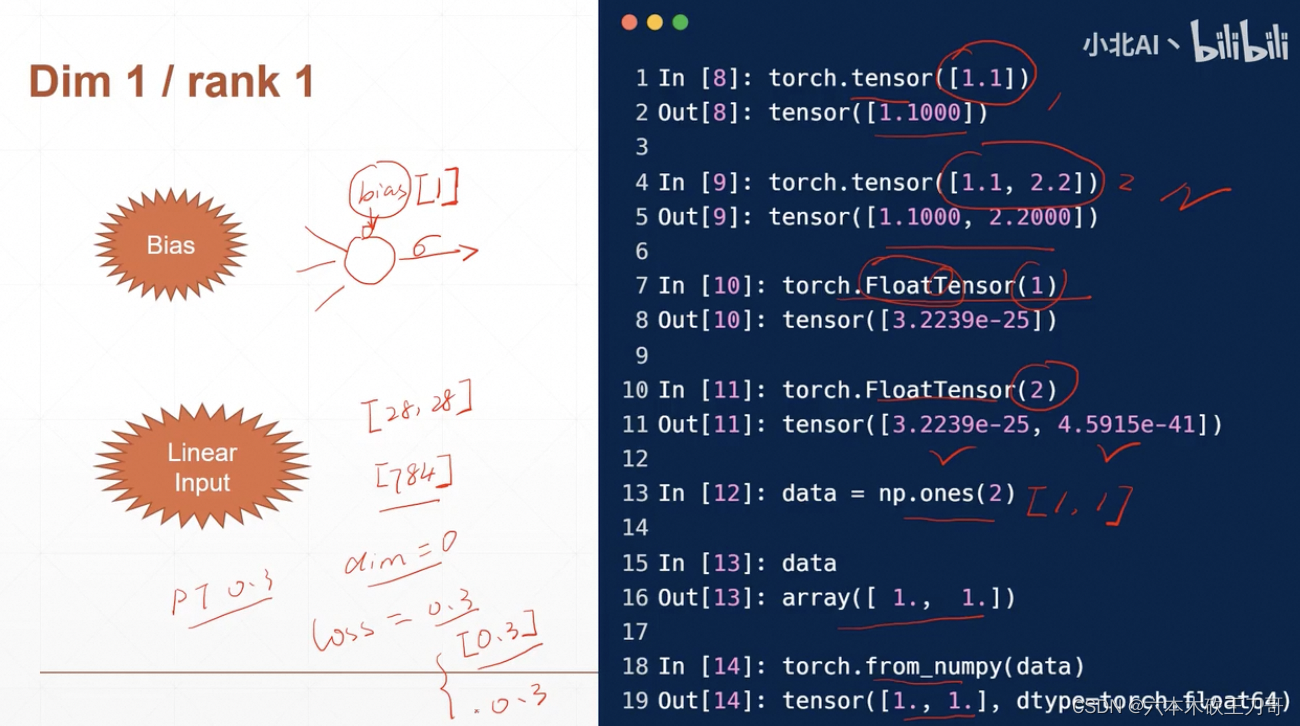
Dimension为1的向量，也就是size可以是多个但是维度必须是1，在PyTorch0.3版本之后，它没法表示一个标量，标量只能用维度为0的Tensor来表示。

一维Tensor的主要用途是在神经网络中加入Bias以及线性输入，例如把一个[28, 28]的Tensor转化为一维然后做输入。

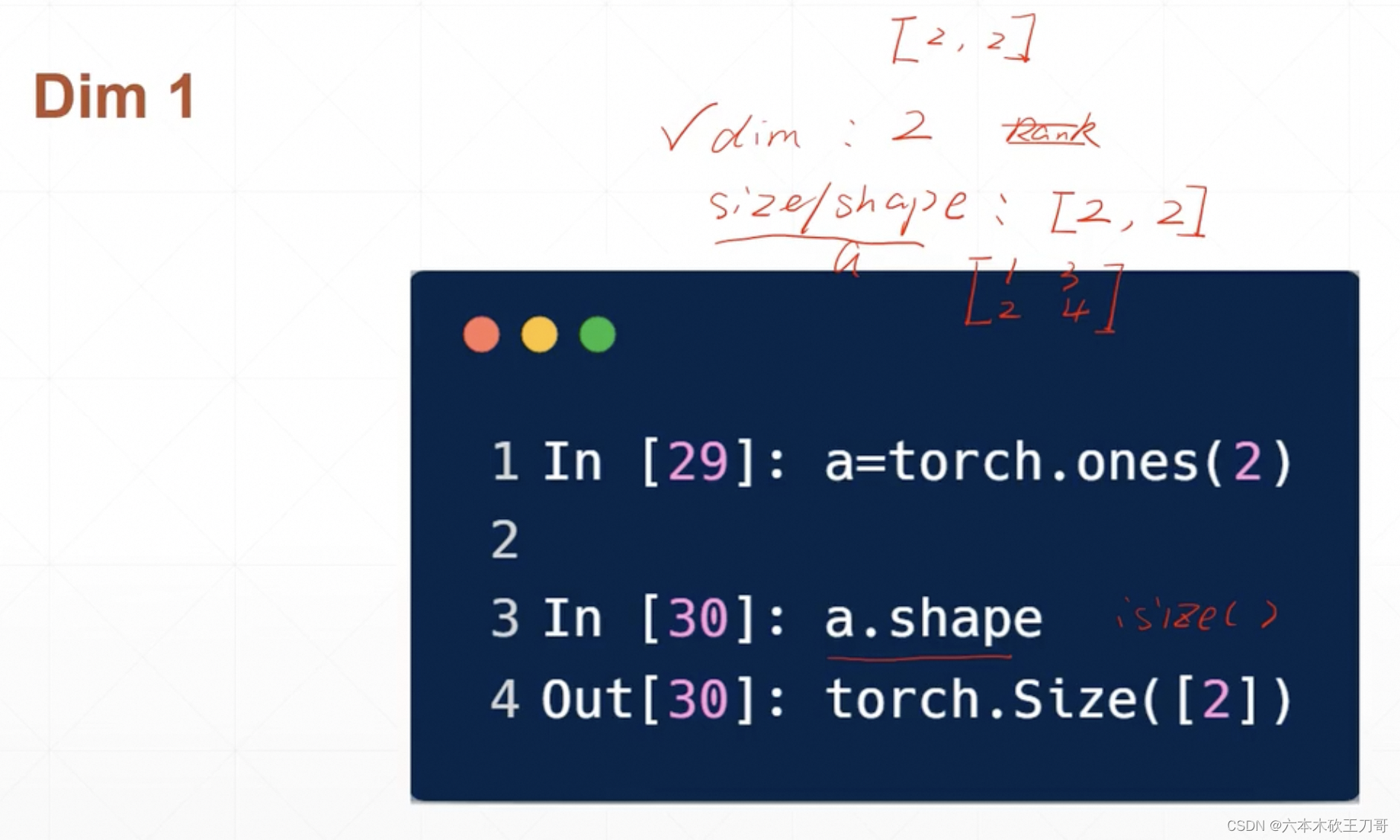
 如何区分Tensor的Size，Shape以及Tensor本身，以Dim=1为例：

 当Dim为2的时候，输出的shape，size都是[2,x]，具体应用就是Linear Batch输入，例如把一堆图片叠加在一起，那么此时Dim=2，Size就是[4,728]

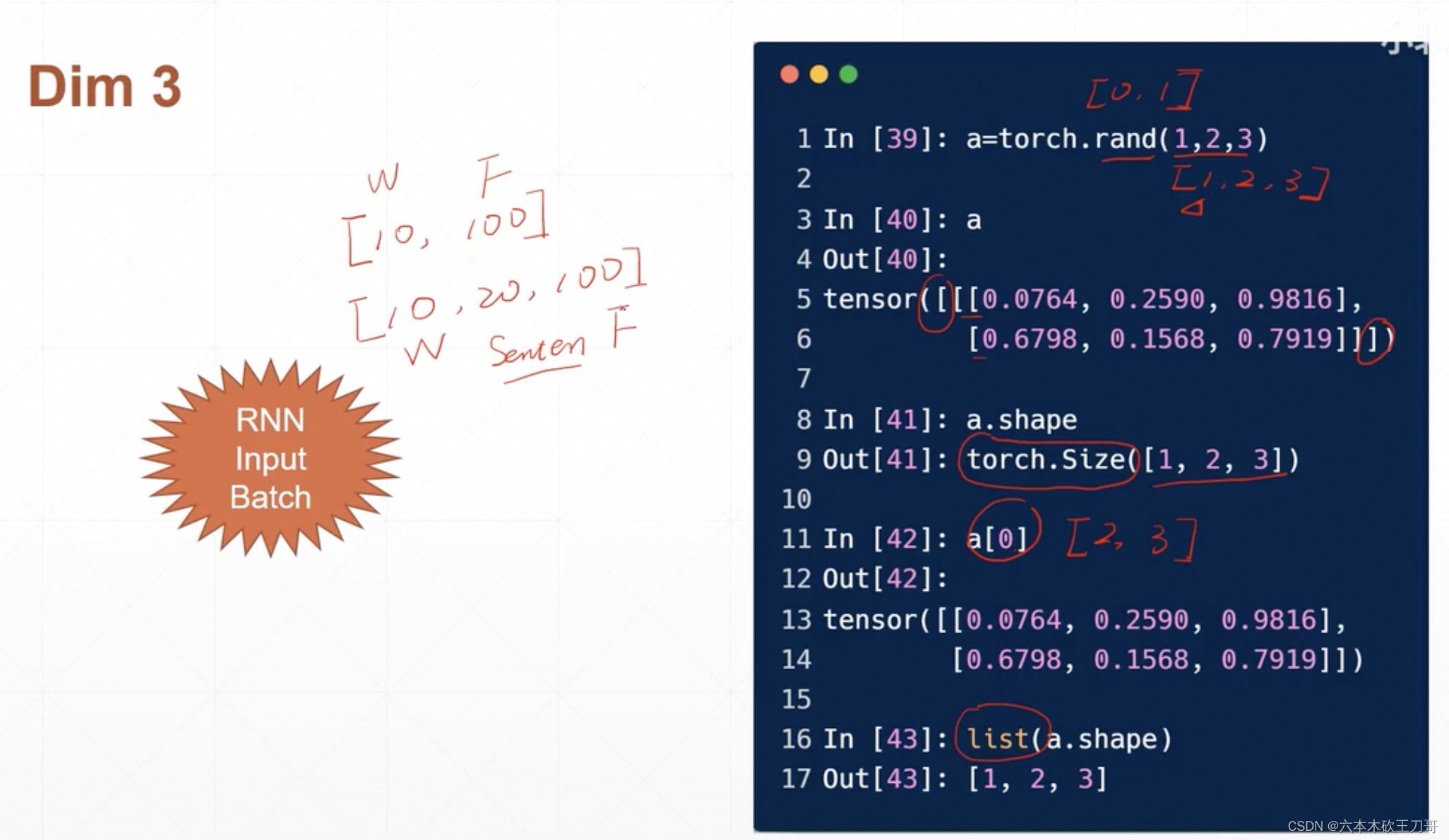
三维输入例子[1,2,3]，第一个维度只有一个[2,3]。主要可以用于RNN的输入，多个句子，每个句子有若干个单词。

四维Tensor，主要可以用来表示多张图片，例如下面就是2张3通道的28X28的RGB图片。

另外也可以使用a.numel()来返回全部元素的个数，用a.dim()直接返回维度而不是用len(a.shape) 

3.创建Tensor

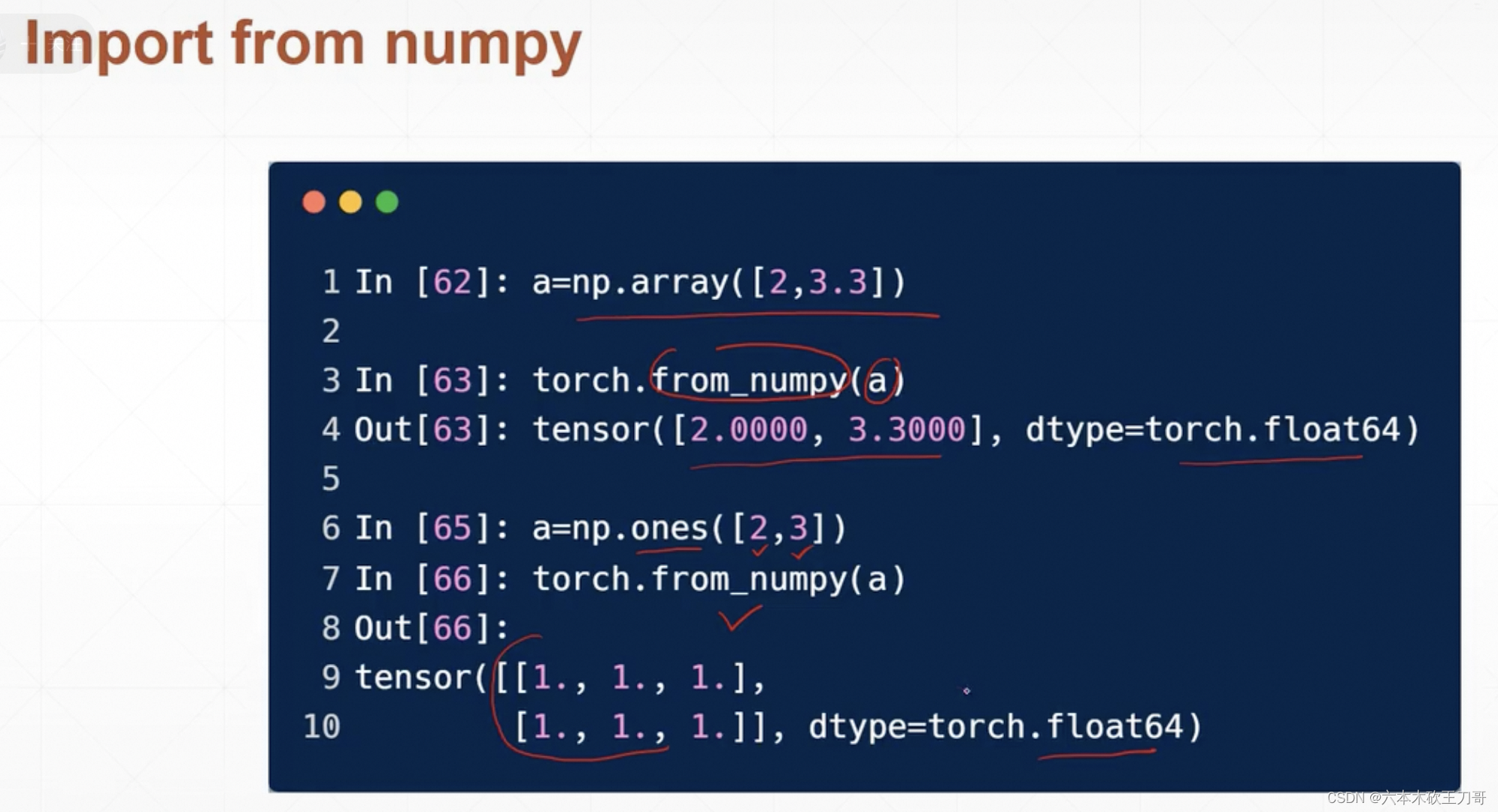
从numpy创建

直接从一个python list创建，把list直接写到torch.tensor()里面，注意这里小写tensor和大写Tensor的区别，大写Tensor()也可以接受shape维度然后创建一个未初始化的张量，一般建议使用小写的直接给list，因为大写Tensor可以接受维度会产生混淆。

生成未初始化的tensor，注意这里传入shape和直接传入list的区别

未初始化举例，生成的数据是不规则的

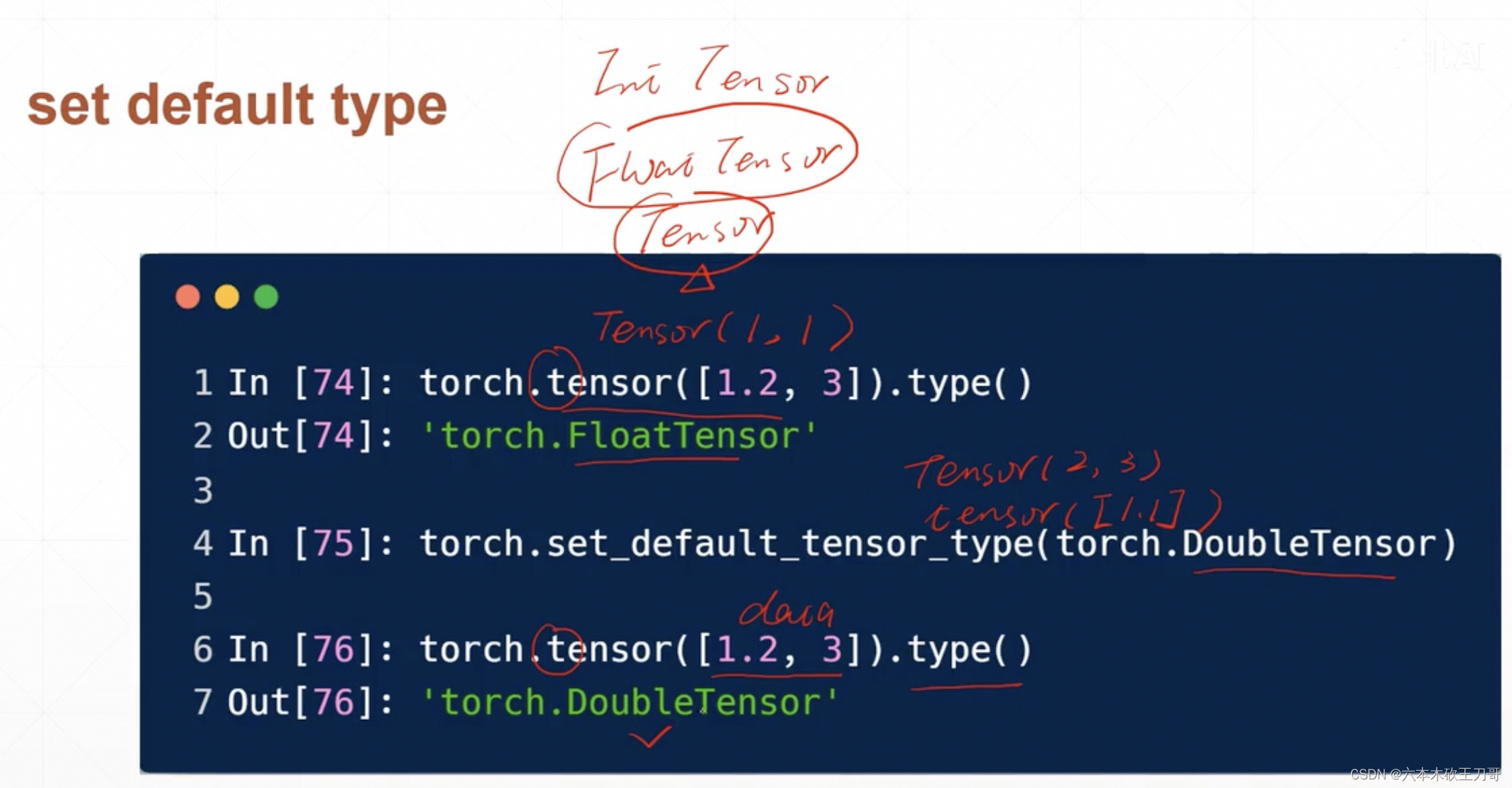
PyTorch中的数据类型默认为FloatTensor，在某些情况下需要转换默认类型

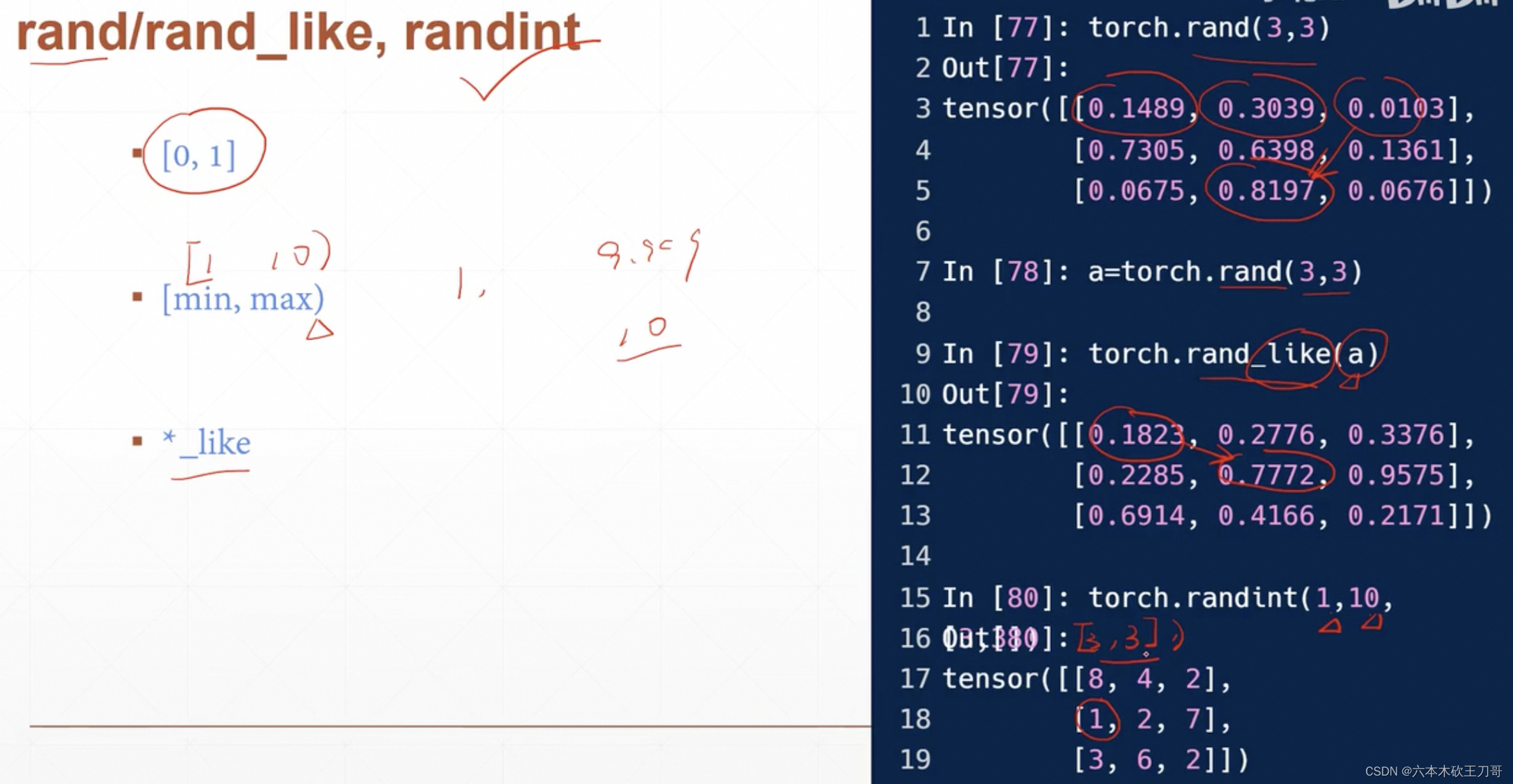
在初始化张量的时候，可以用rand来限制范围，rand是从0～1之间随机采样的函数，rand_like是输入一个张量，获得维度之后再rand出对应维度的张量，另外也可以用randint来限制随机的范围

 使用randn和normal创建采样自正态分布的tensor，相对来说normal使用起来不太方便

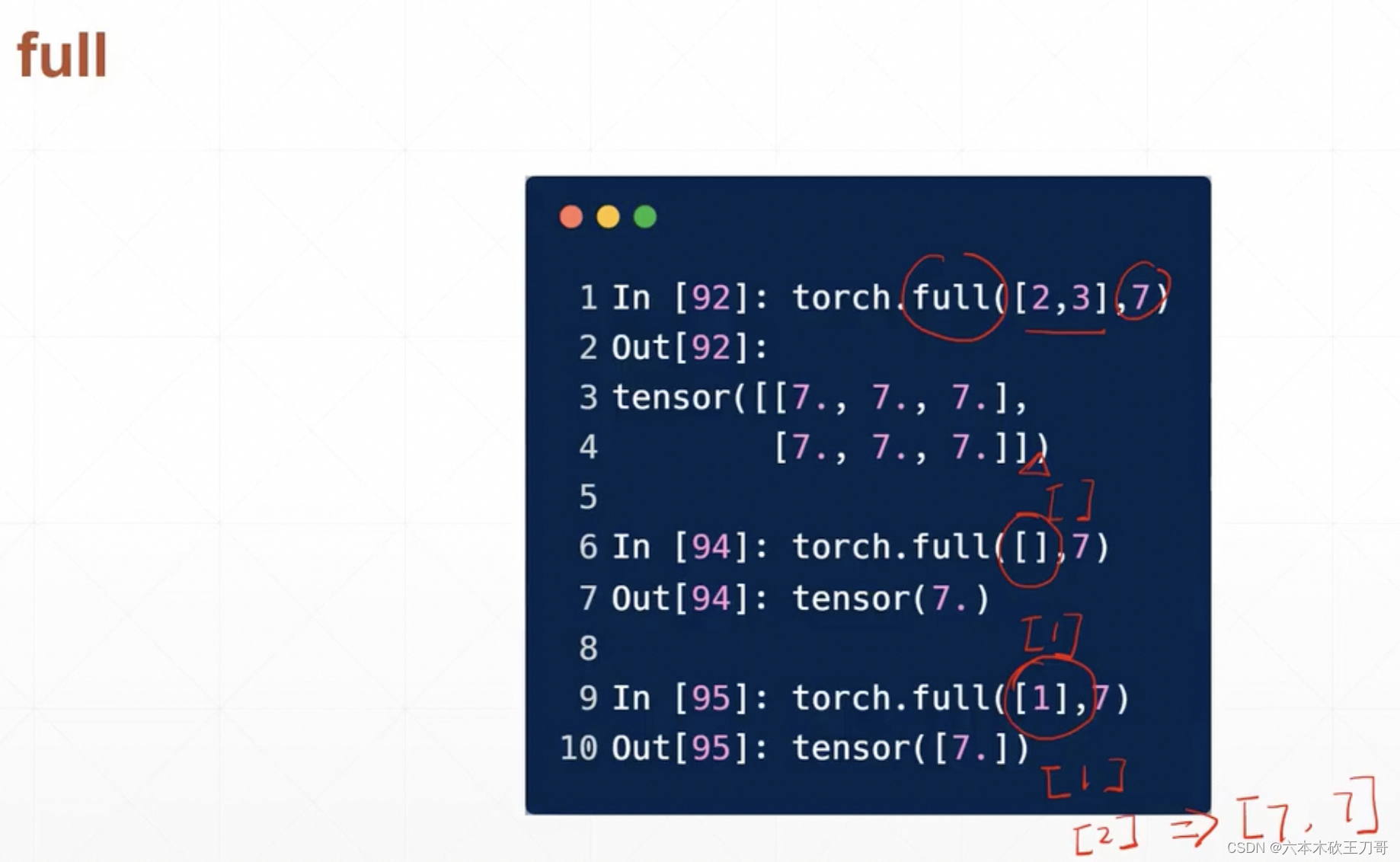
用full来生成全部元素一样的tensor

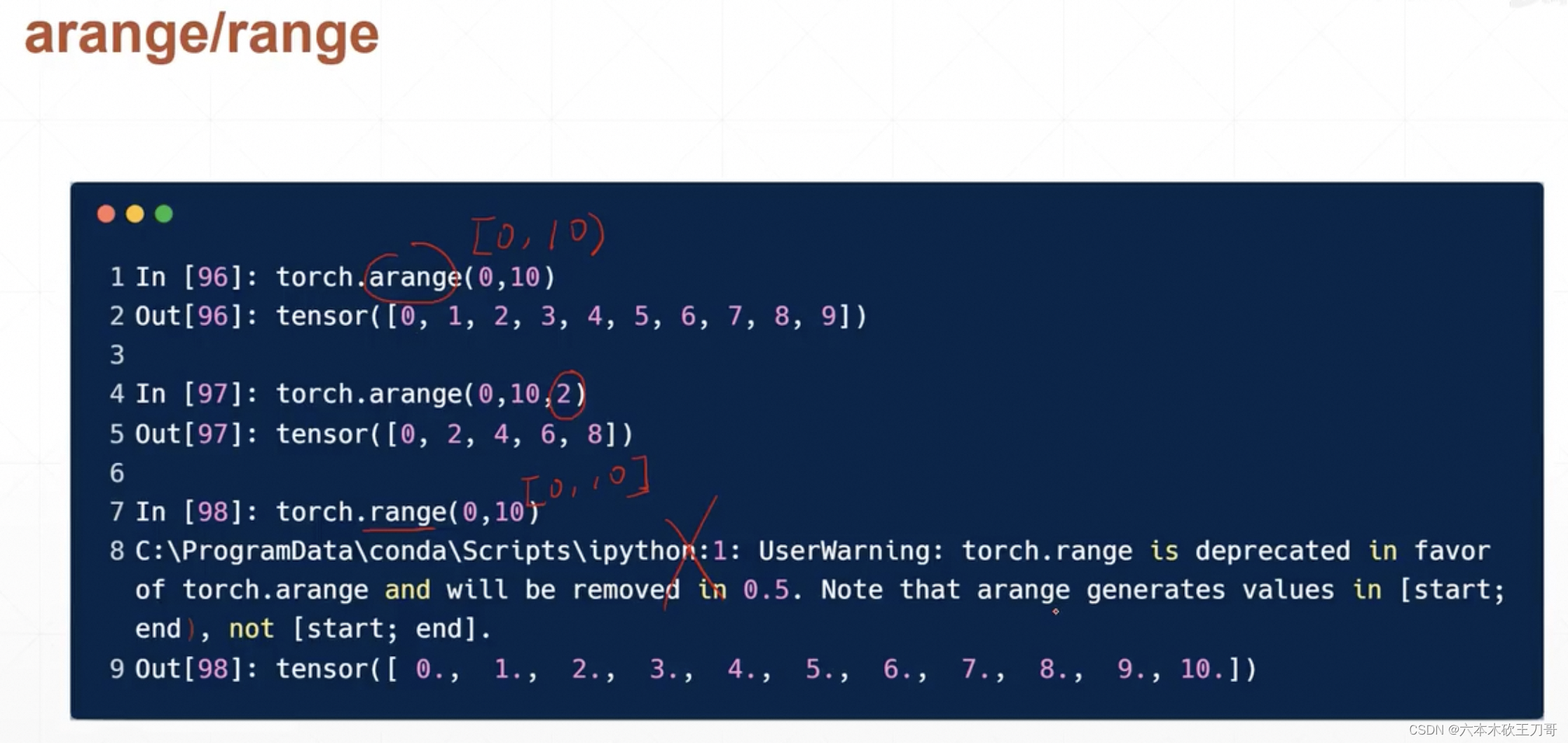
用arange来生成递增元素的tensor

linspace和logspace是用来切割数据，例如linspace设置范围是0-10，steps是4，那么就是从0到10分成4份，另外logspace是分成若干份，然后结果是10的x次，例如0到-1分成10份，然后每个数放在10的幂位置上。

生成全0，全1，和对角线的api，其中eye只接受一个或者两个参数，它只适合一个矩阵不适合更高维度的tensor。

4.梯度

4.1 梯度的概念

对于一个函数来说（或者是Loss函数），导数就是一个数，而梯度就可以理解为一个向量。

4.2 激活函数的梯度

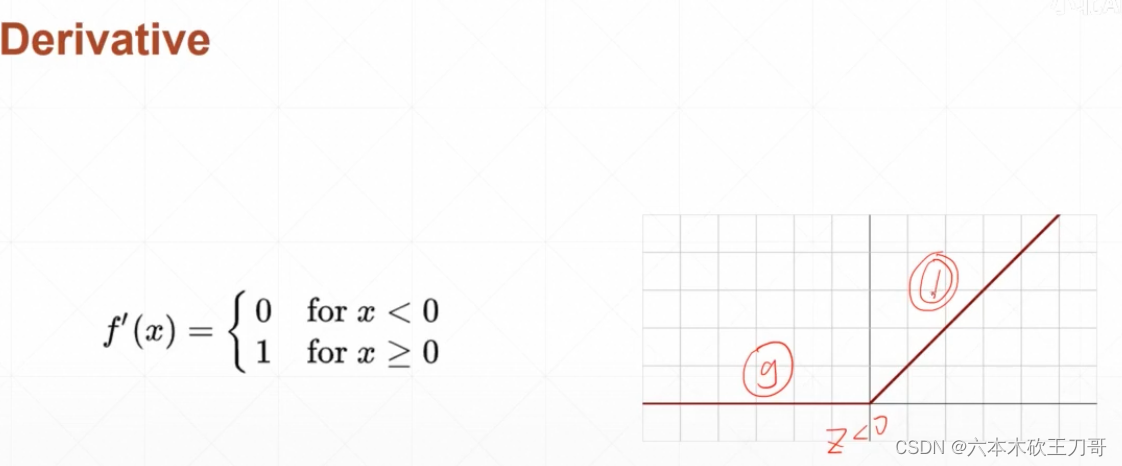
最开始用的时候阶梯函数，但是阶梯函数不可导，所以无法使用梯度下降找最优解。

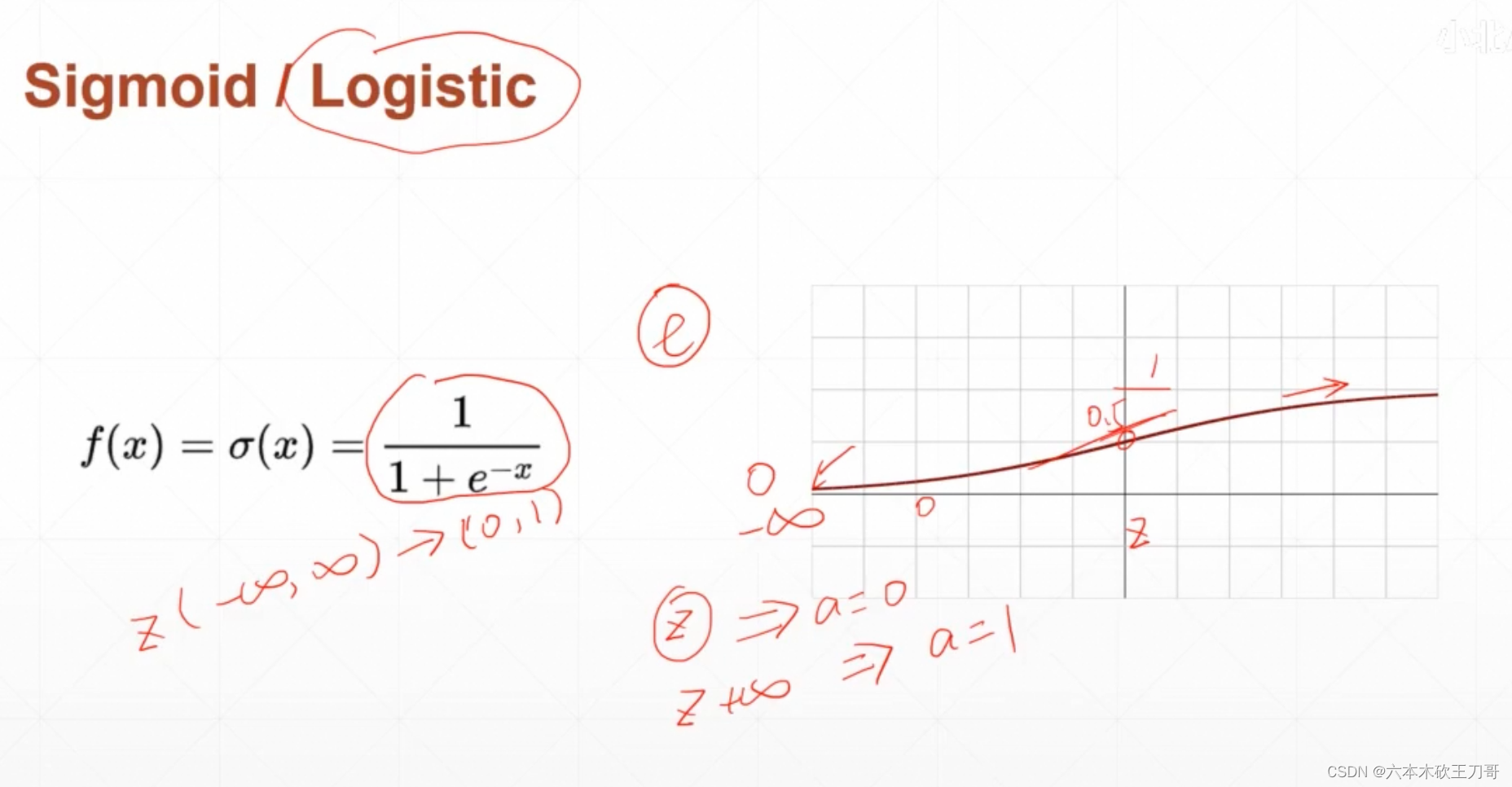
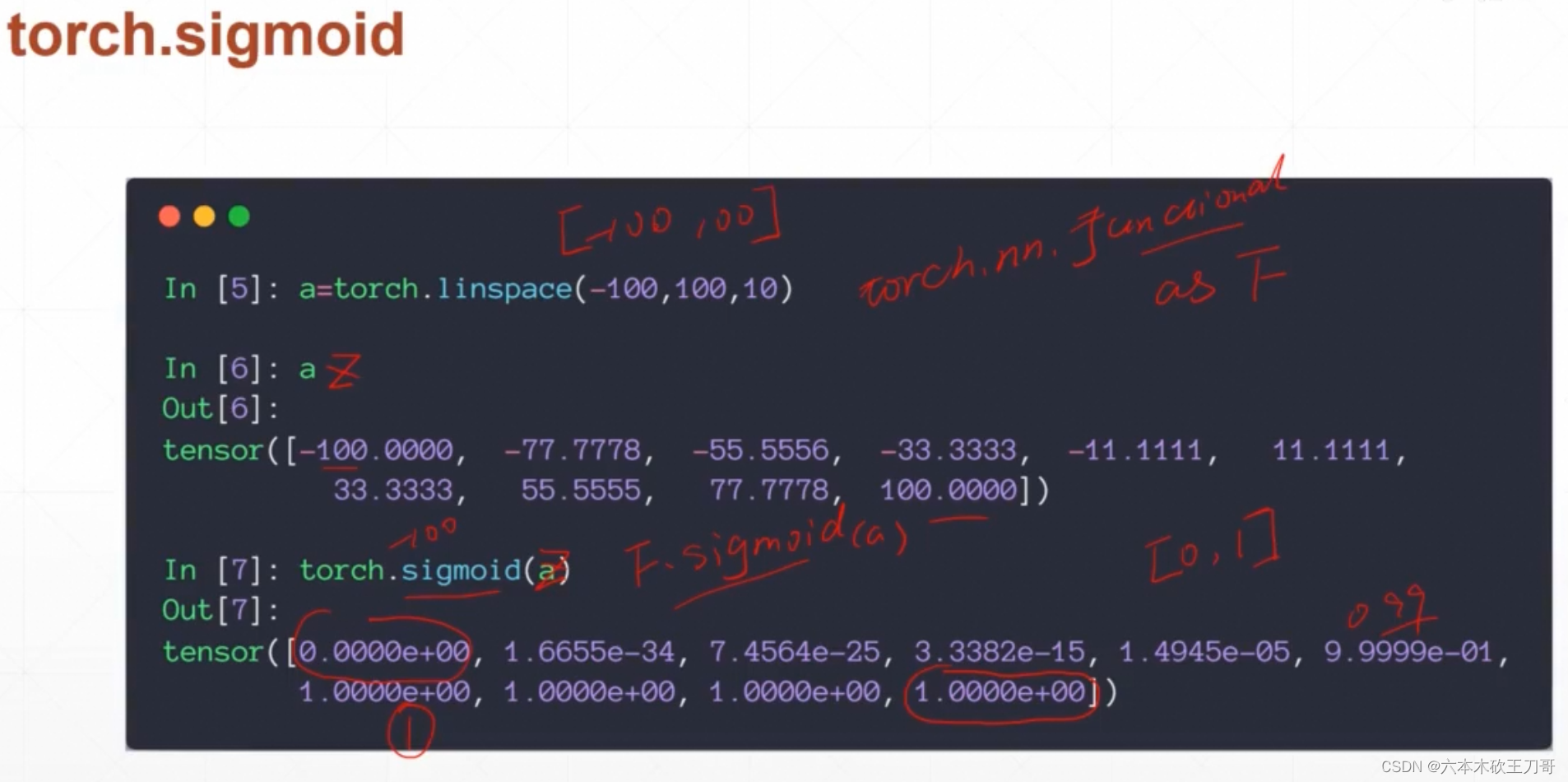
下一个激活函数是Sigmoid函数，这个函数在生物学中比较形象，对于很大或者很小的输入，生物的反应肯定是限制在一个范围内。

求Sigmoid函数的导数，导数的值非常有用，因为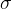的值前向计算的时候是已知的，所以对于导数来说也是已知的。

但是Sigmoid有个致命的问题就是在输入值很大或者很小的时候，导数趋于0，会使得梯度一直得不到更新。

另外一种激活函数是Tanh

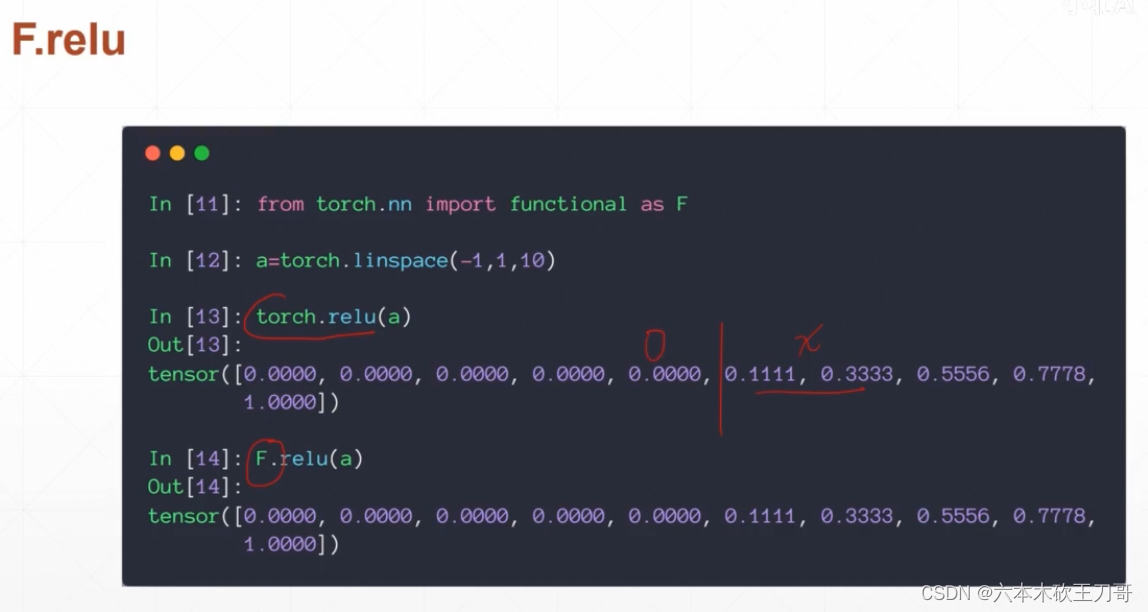
用得最多是整型线性单元ReLU，虽然和平时的生物感应不太一样，但是他特别适合深度学习，因为它在大于0的时候梯度一直是1，这样就很少出现梯度离散和梯度爆炸的情况

 4.3 Loss的梯度

注意MSE的Loss和L2Norm的区别是有没有开根号，使用torch.norm写Loss要pow2

对线性函数用PyTorch求导的过程：

pred = x*w + b，设置x=1，w=2，b=0

直接从Function中获得mes_loss，然后参数是预测值和真实值，但是写反也可以。

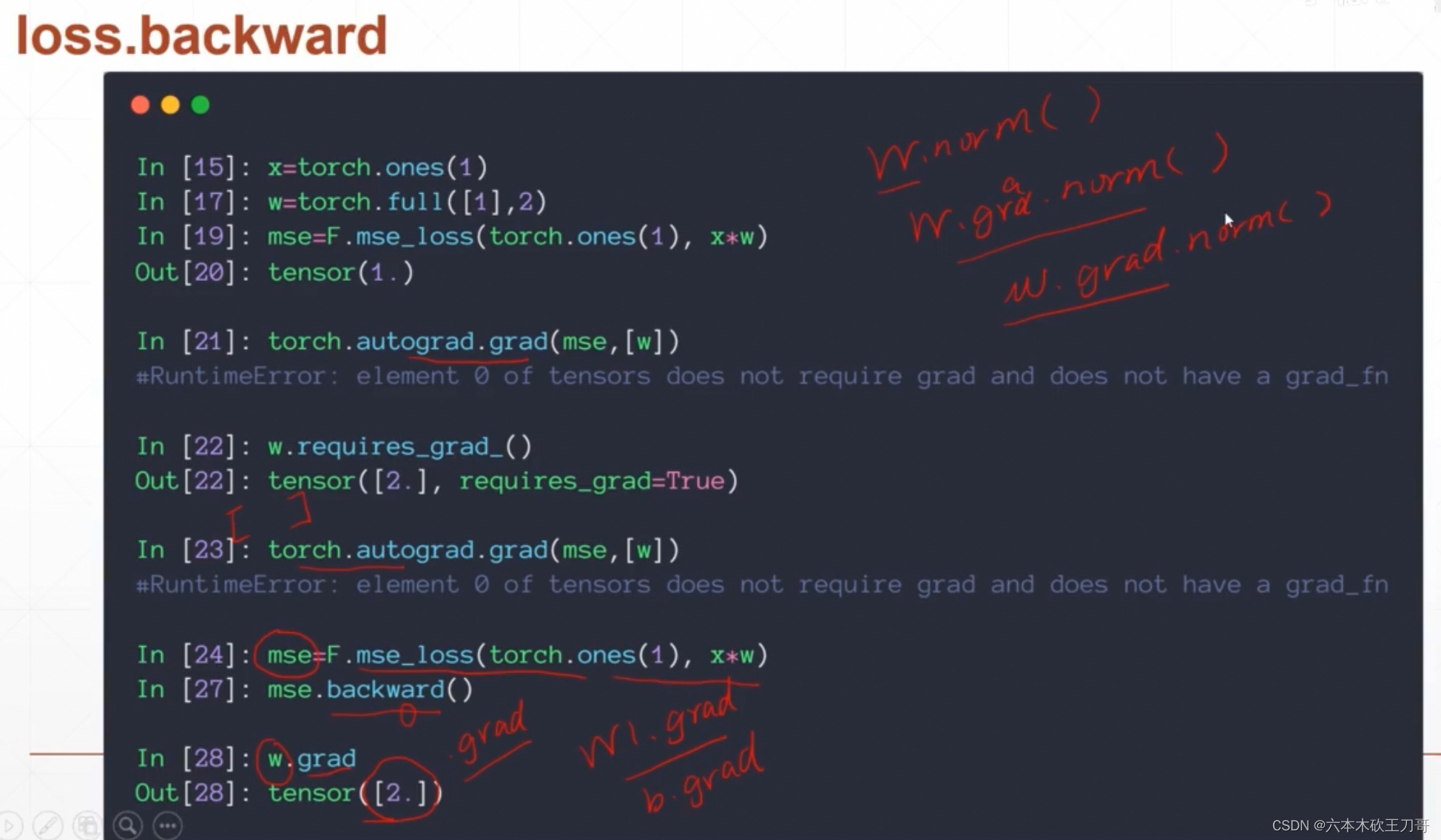
然后用autograd求w的梯度，但是这里会报错，因为最开始mse建图的时候w默认是不带梯度的，需要设置w为需要记录梯度，但是还是会报错因为图还是原来的图，需要重新求一次loss才可以

接下来用backward来求导，它的原理是得到Loss之后，反向传播一次，记录每个需要求导的参数的梯度，把它记录到其对应的grad变量中，如果要查看这个梯度，就可以直接调用.grad来查看，注意有时候需要查看梯度的norm，使用w.grad.norm()

总结下面两种求梯度的API 

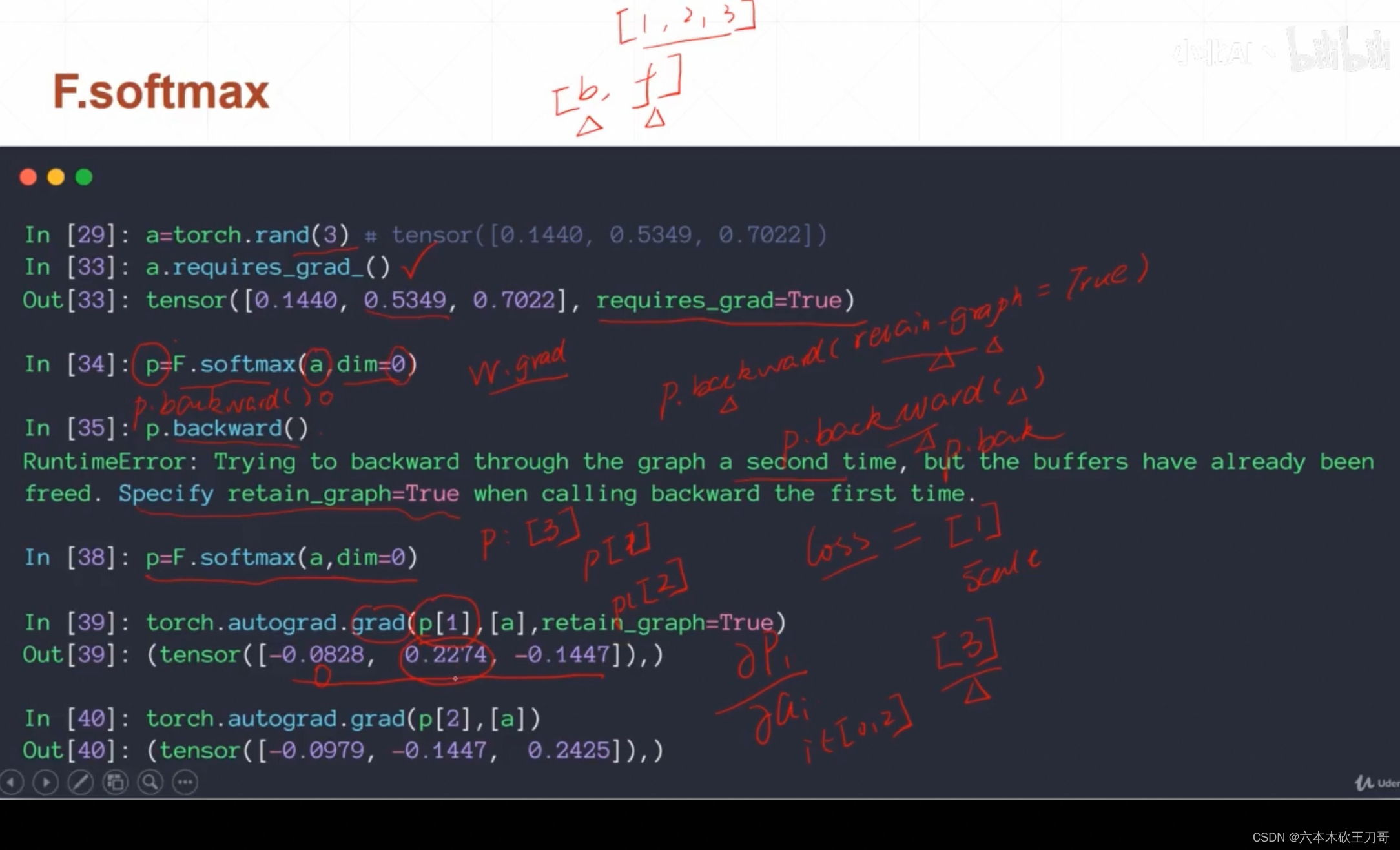
 求Softmax激活函数的梯度，可以发现如果i和j相等的时候

其中Pj在前向传播的时候就已经知道了，所以反向传播的时候就可以直接计算出梯度

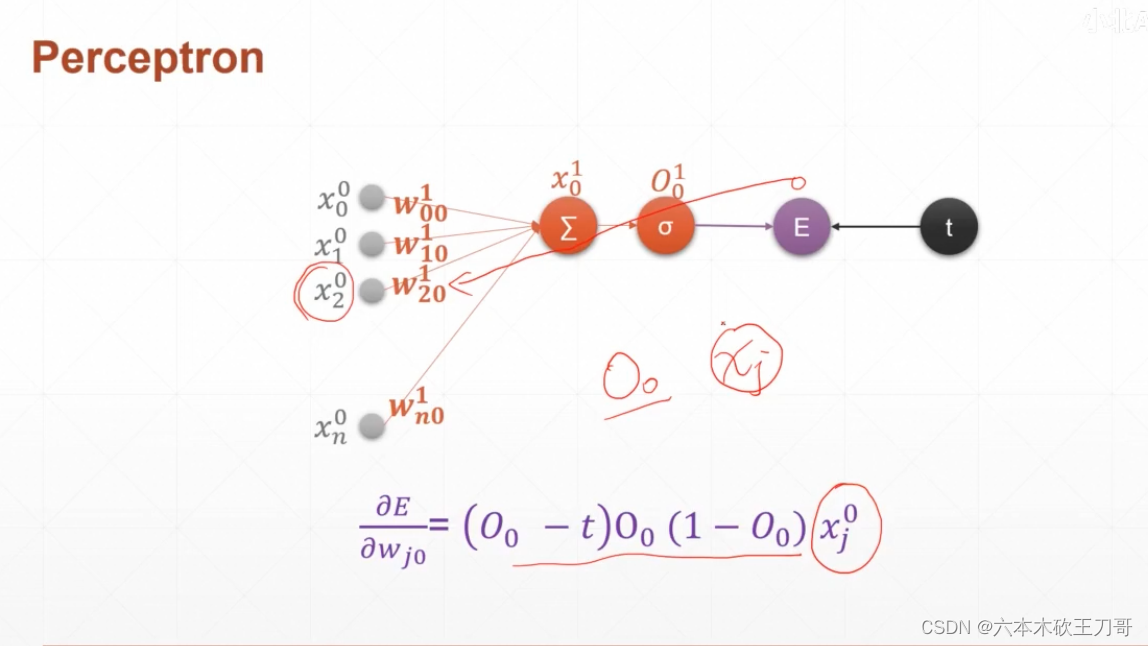
 当i不等于j的时候，求偏导得

总结如下，例如输入三个输出三个，每个节点相互之间对应的偏导有正负的区别

用PyTorch求解的过程，先生成Size为3的tensor，因为是分类问题，然后设置需要梯度。注意在反向传播的时候需要保持之前的图，之后在直接用autograd求梯度而不是反向传播的时候，需要传入的Loss必须是一维Size为1或者是0维的，这样输出出来这个Loss对三个输出a1，a2，a3的梯度就可以算出来了。

用Pytoch再次求解一个具体例子，可以看到对应的梯度符合之前推导的公式

>>> a=torch.rand(3)
>>> a.requires_grad_()
tensor([0.1103, 0.7891, 0.0804], requires_grad=True)
>>> p=F.softmax(a, dim=0)
>>> p
tensor([0.2537, 0.5001, 0.2462], grad_fn=<SoftmaxBackward0>)
>>> torch.autograd.grad(p[1], [a])
(tensor([-0.1269,  0.2500, -0.1231]),)
>>> -0.2537*0.5001 # -Pi*Pj
-0.12687537
>>> 0.5001*(1-0.5001) # Pi*(1-Pj)
0.24999999

4.4 感知机的梯度

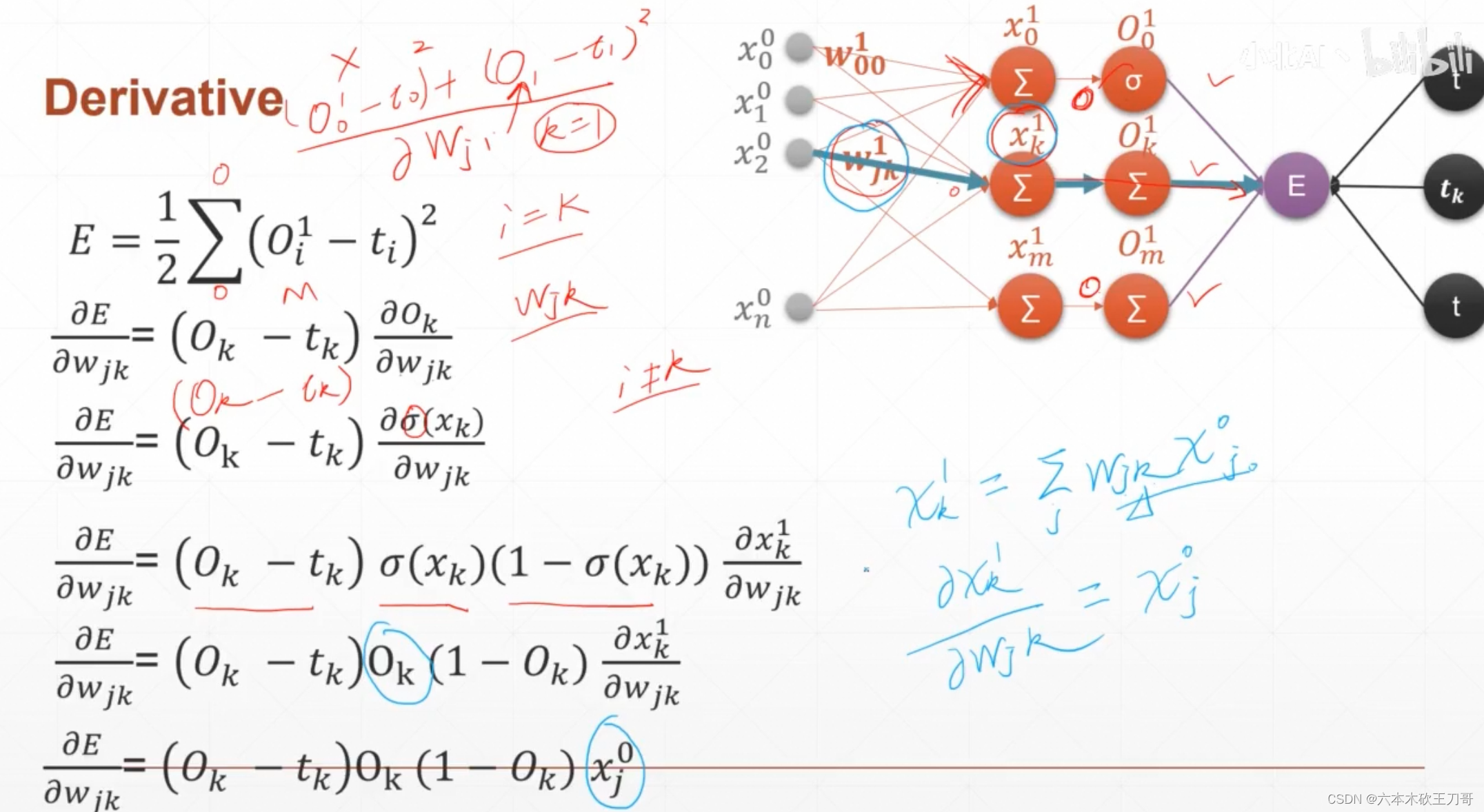
单层感知机推导

 最终对某个参数的梯度只与这个参数对应的输入值和输出值有关系（激活函数是Sigmoid函数）

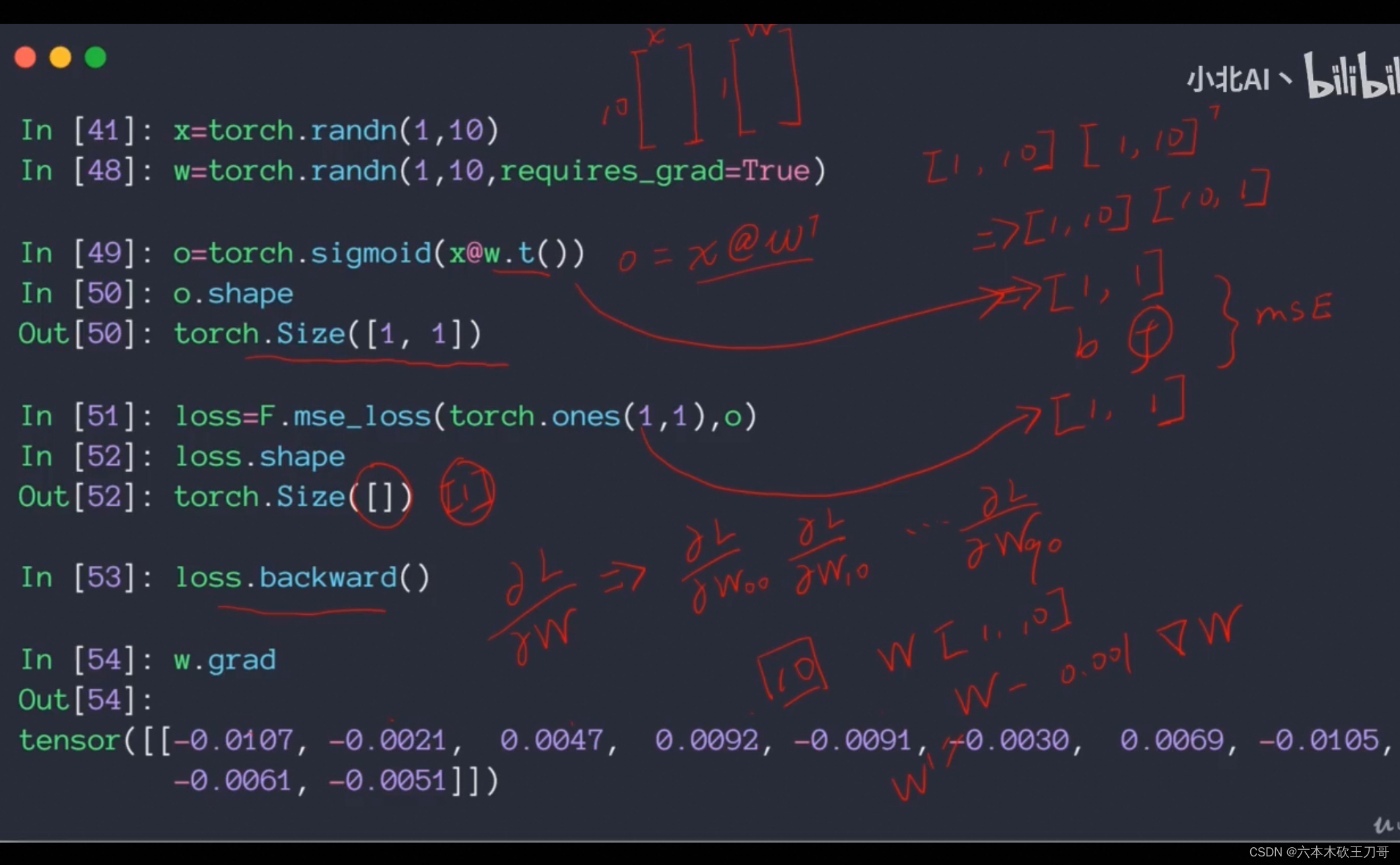
用Pytorch计算输入是一维且Size为10的Tensor，其中w参数也是一维且Size为10，计算经过Sigmoid激活函数的输出时，w的Tensor需要做一个转置，得到一个标量输出，对这个标量输出与目标值做一个MSE求得Loss，再对这个Loss反向传播，就可以得到w的梯度向量

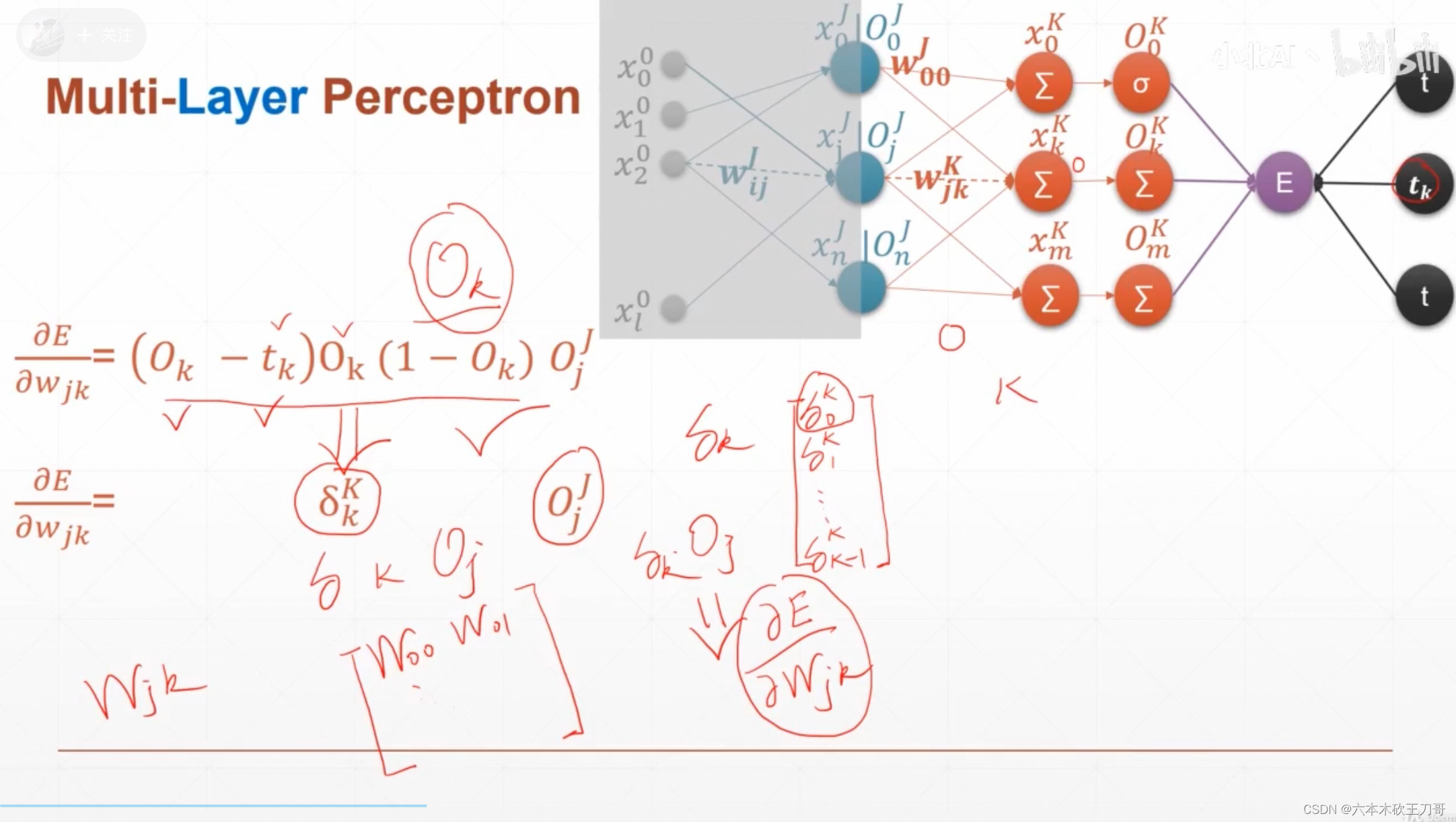
多层感知机推导

此时不止一个梯度，均方误差的公式会有变化

推导出的公式和单层很类似

使用Pytorch求解，输出x是1x10维度，输出是1x2维度，所以参数就是2x10维度，w参数和x输入矩阵做乘法，可以得到1x2的输出Tensor。求MSE-LOSS的时候需要注意目标Pred也必须是1x2的，这样可以对应的上。

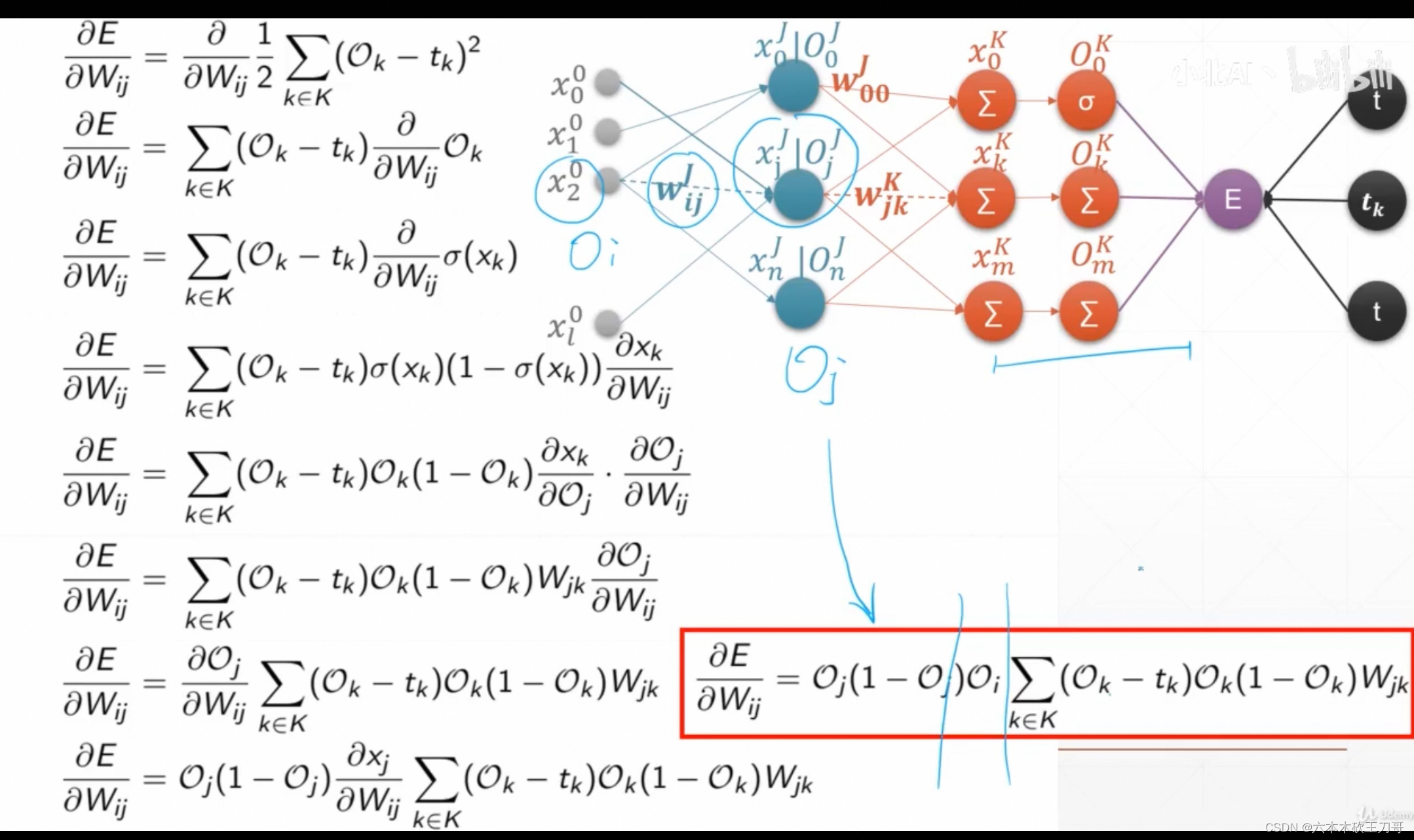
链式法则

增加了中间一层，可以使用链式法则来求解

通过链式法则来验证是否成立

反向传播实战推导

先从倒数第一层求导开始，简化与k相关的参数为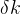，因为对于Wjk这个权重，前面是j节点，后面是k节点，对于k节点来说，他的输出Ok和预测值tk都是在前向计算中已知的，所以整个式子都可以表达为一个

 对倒数第二层求偏导

总结关系

4.5 2D函数梯度下降优化求最值

先定义一个具有四个最小值为0的函数

然后用Pytorch梯度下降，用Adam优化器来更新x和y，更新准则就是减去lr*梯度，进入循环之后，先得到预测值（就是函数的真实值，这里需要最小化这个预测值），然后梯度清零，再反向传播一次求梯度，然后通过优化器step一次更新x和y，打印x（其实是x和y）的list和fx。

5.交叉熵 

因为用于二分类的逻辑回归已经用的不多了，所以这里不记录。

描述熵，KL散度和交叉熵的文章：https://www.cnblogs.com/wuliytTaotao/p/9713038.html

用代码实例去计算：熵，交叉熵，KL散度公式与计算实例 - 知乎

 验证交叉熵的代码，其中p和q是两个分布，p可以理解为实际分布，q为近似分布。

import torch
import numpy as np
from torch.distributions import Categorical, kl

# Cross entropy
p = [0.1, 0.2, 0.3, 0.4]
q = [0.1, 0.1, 0.7, 0.1]

Hpq = -sum([p[i] * np.log(q[i]) for i in range(len(p))])
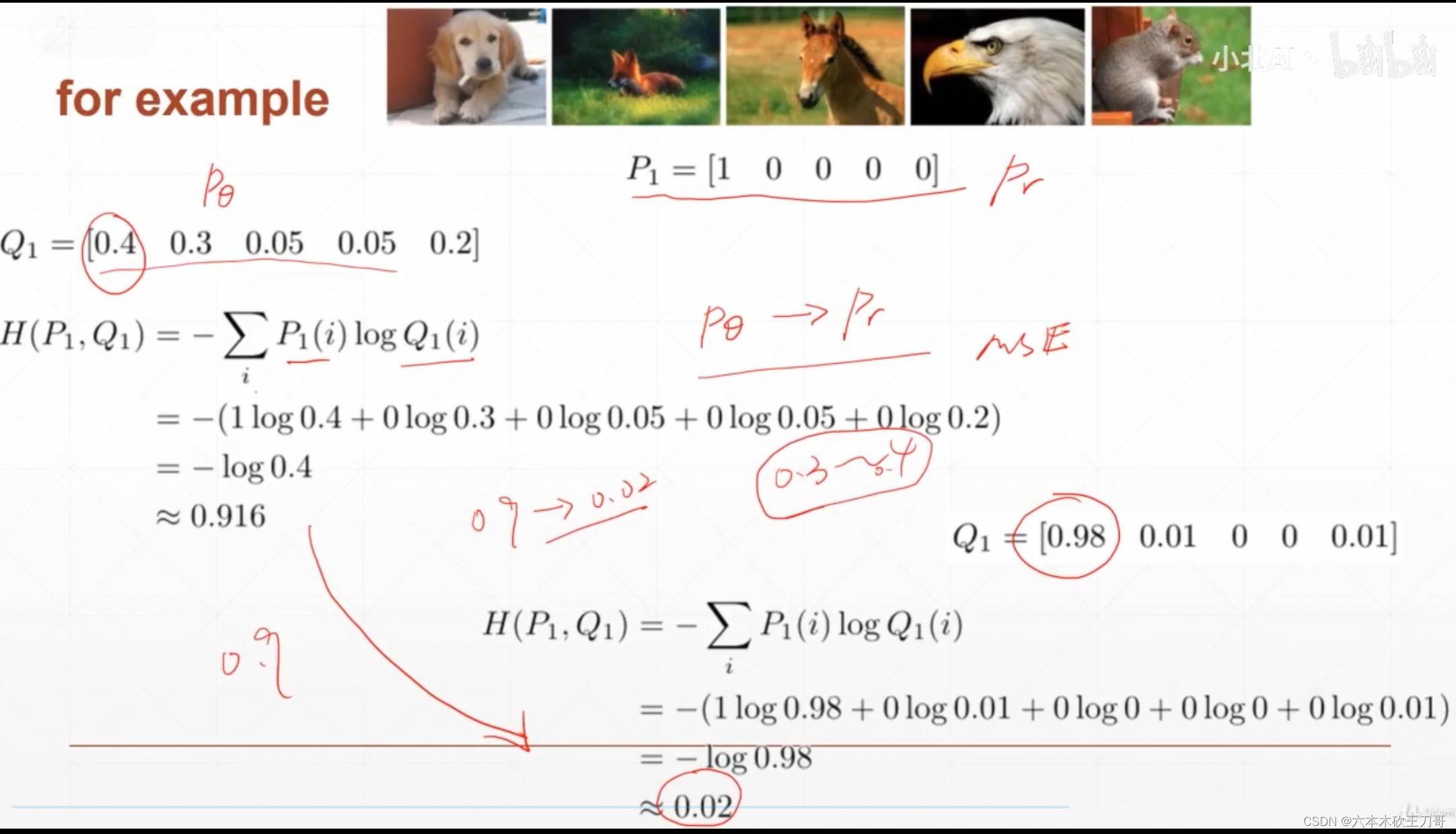
print (f"H(p, q) = {Hpq}")

 用一个例子说明，P是实际分布，Q是我们需要优化的近似分布，第一次Q1求得交叉熵为0.916，此时预测效果还不好，第二次优化之后Q1优化效果变好了，交叉熵的值降低为0.02，这样降低的熵比起MSE来说更大一些，所以更适合用交叉熵来优化。

输出线性层之后是一组logits，然后进入Softmax层，其中交叉熵计算是匹配Softmax的Loss函数

在Pytorch中，Softmax层和交叉熵层是合在一起的，所以在写代码的时候，需要在cross_entropy函数中直接传入logits，因为这个ce是由softmax+log+nll_loss组成的，如果要自己手动写的话，就要写完整这三个函数。

6.多分类问题实战

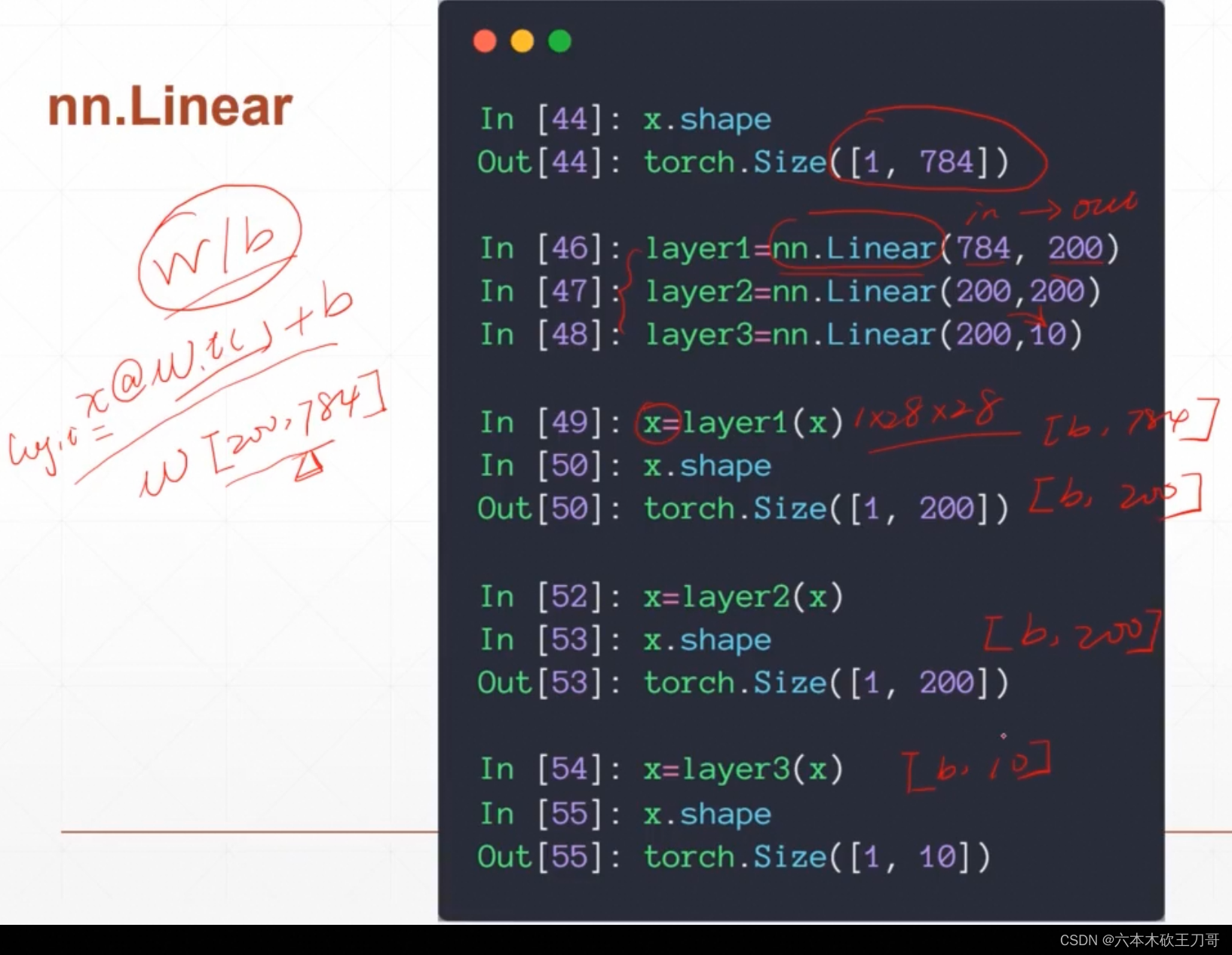
6.1 直接定义网络和输入输出

新建一个网络结构，748是28x28的图片结构，然后输出是200，最后一层是200x10，因为是有10个分类。

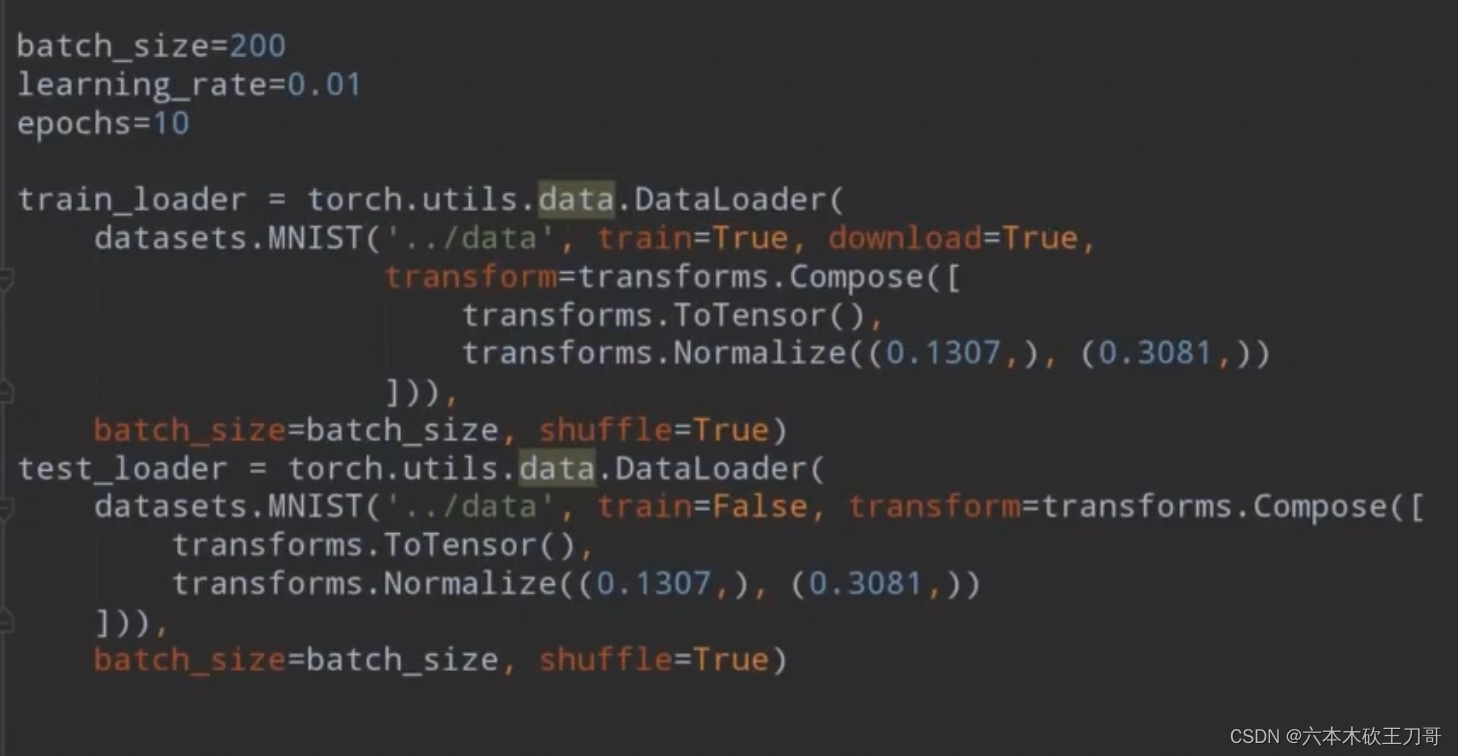
加载数据代码

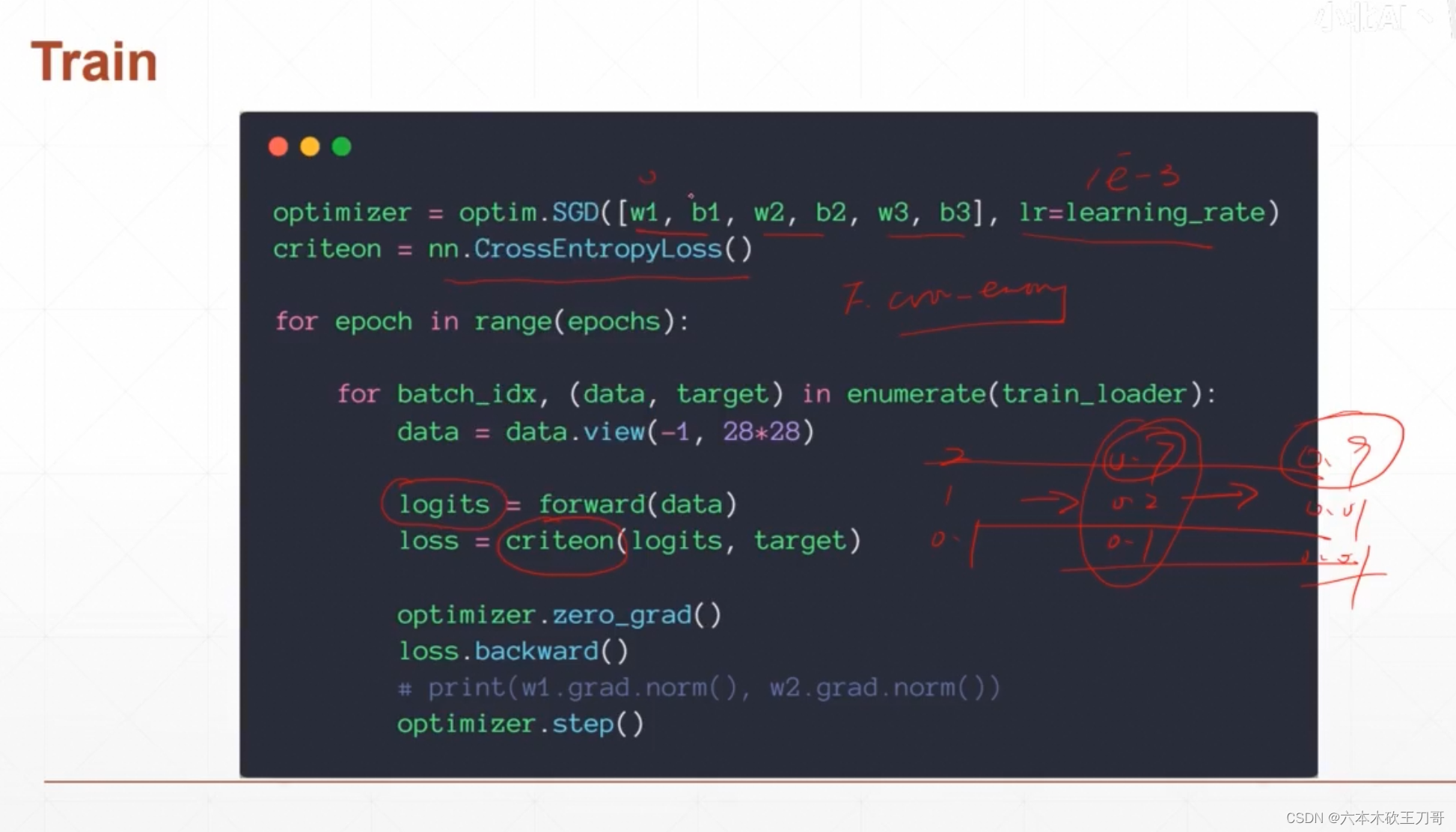
训练代码

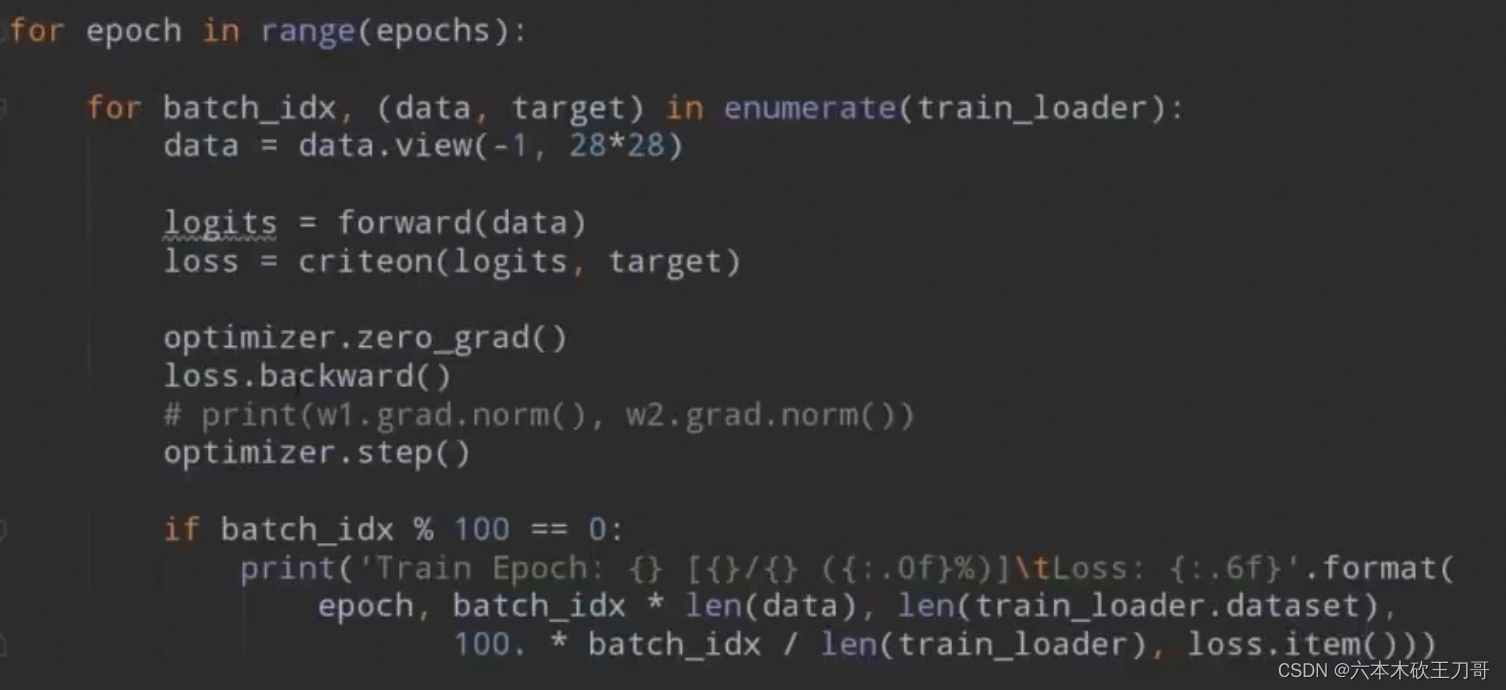
剩余代码：

记得需要初始化，不然可能会出现梯度一直没法更新的情况

完整代码：

import  torch
import  torch.nn as nn
import  torch.nn.functional as F
import  torch.optim as optim
from    torchvision import datasets, transforms


batch_size=200
learning_rate=0.01
epochs=10

train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, transform=transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize((0.1307,), (0.3081,))
    ])),
    batch_size=batch_size, shuffle=True)



w1, b1 = torch.randn(200, 784, requires_grad=True),\
         torch.zeros(200, requires_grad=True)
w2, b2 = torch.randn(200, 200, requires_grad=True),\
         torch.zeros(200, requires_grad=True)
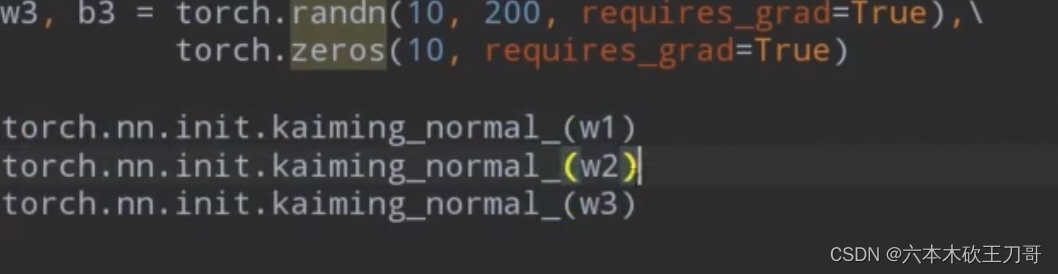
w3, b3 = torch.randn(10, 200, requires_grad=True),\
         torch.zeros(10, requires_grad=True)

torch.nn.init.kaiming_normal_(w1)
torch.nn.init.kaiming_normal_(w2)
torch.nn.init.kaiming_normal_(w3)


def forward(x):
    x = [email protected]() + b1
    x = F.relu(x)
    x = [email protected]() + b2
    x = F.relu(x)
    x = [email protected]() + b3
    x = F.relu(x)
    return x


optimizer = optim.SGD([w1, b1, w2, b2, w3, b3], lr=learning_rate)
criteon = nn.CrossEntropyLoss()

# train_loader.dataset is 60000, train_loader is 300.
print('train_loader.dataset is {}, train_loader is {}.'.format(len(train_loader.dataset), len(train_loader)))

for epoch in range(epochs):
    
    # enumerate函数会给出数据索引batch_idx和数据值(data, target)
    for batch_idx, (data, target) in enumerate(train_loader):
        # 每次循环一个batch，data最初的Size是[200, 1, 28, 28]
        # 重新组织Tensor，-1代表这个维度自动推断，这里是batch的大小200x1
        data = data.view(-1, 28*28)

        logits = forward(data)
        loss = criteon(logits, target) ##loss是一个batch的loss和

        optimizer.zero_grad()
        loss.backward()
        # print(w1.grad.norm(), w2.grad.norm())
        optimizer.step()

        if batch_idx % 100 == 0:
            print("data size:") 
            print(data.size()) # torch.Size([200, 784])
            print("logits size:")
            print(logits.size()) # torch.Size([200, 10])
            print("target size:")
            print(target.size()) # torch.Size([200])

            # Train Epoch: 0 [40000/60000 (67%)]	Loss: 0.791112
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item()))


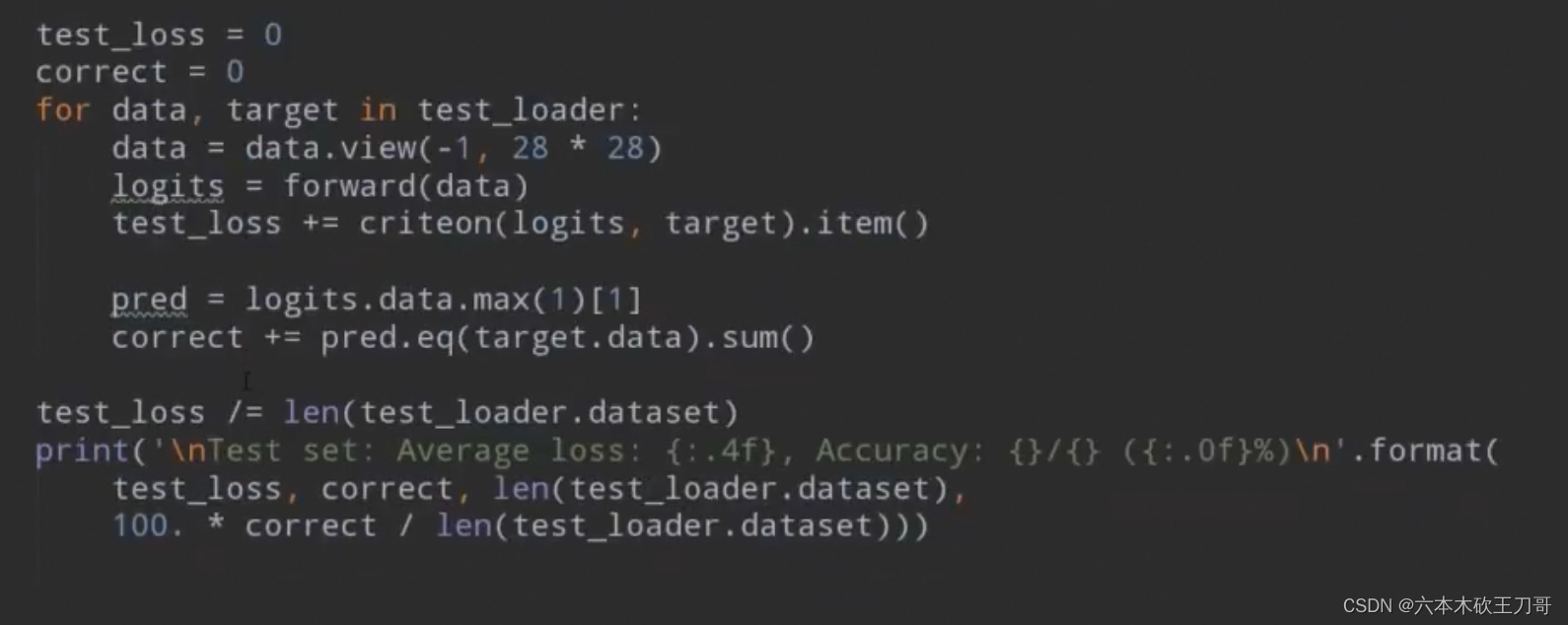
    test_loss = 0
    correct = 0
    for data, target in test_loader:
        data = data.view(-1, 28 * 28)
        logits = forward(data)
        test_loss += criteon(logits, target).item()

        # 用于从logits中获取每一行的最大值对应的索引
        pred = logits.data.max(1)[1]
        correct += pred.eq(target.data).sum()

    test_loss /= len(test_loader.dataset)
    
    # Test set: Average loss: 0.0019, Accuracy: 8943/10000 (89%)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

上述网络的参数w和b都需要自己定义，这样会非常繁琐，所以下面使用提供的API来进行计算

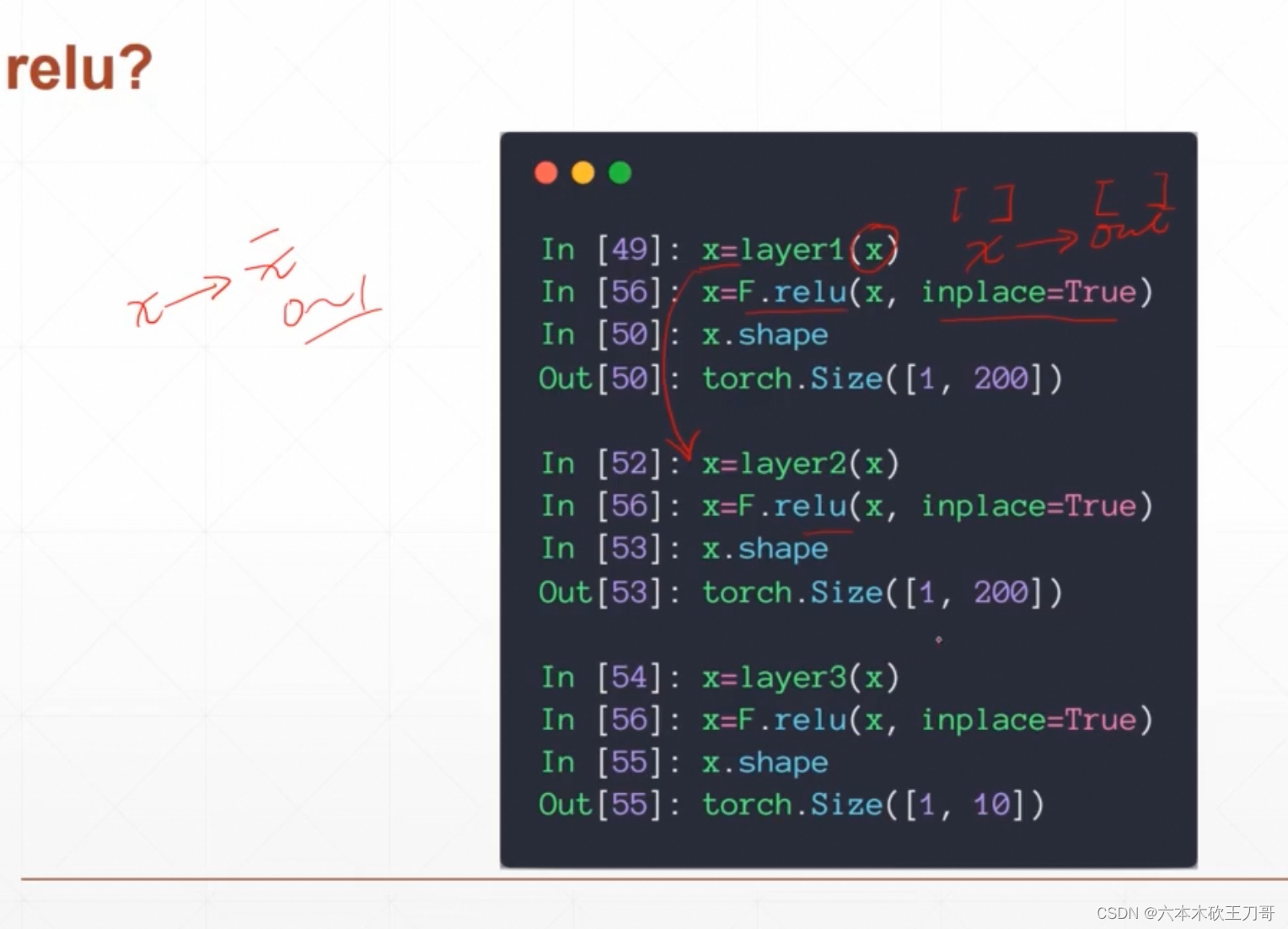
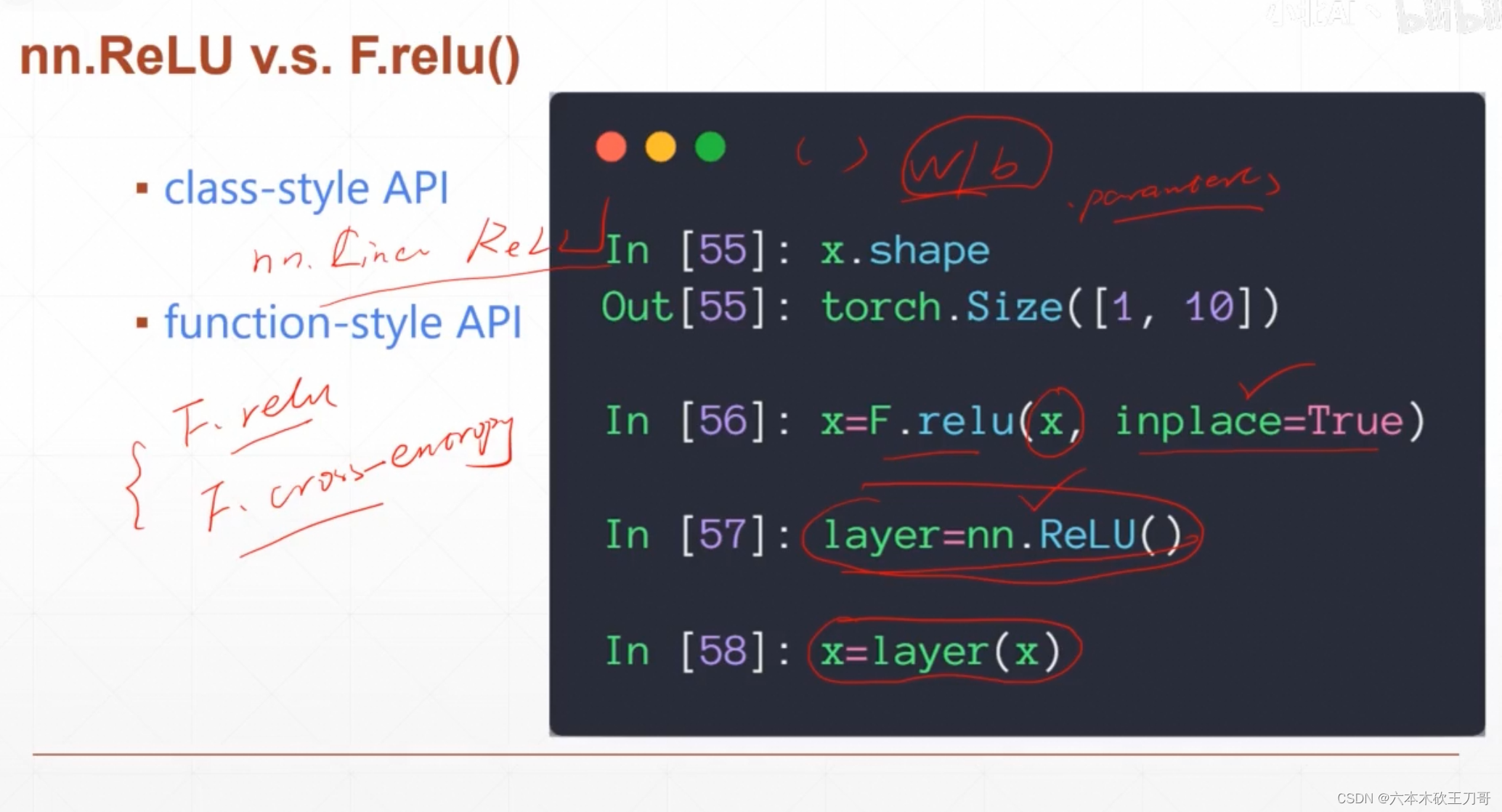
接下来可以增加一些激活函数，下面relu函数所加的inplace操作只为了节省内存，因为relu对应的输入x和输出x的维度是一样的，所以可以节省掉一半内存

6.2 更加精简的做法

通过Pytorch提供的类和接口来实现

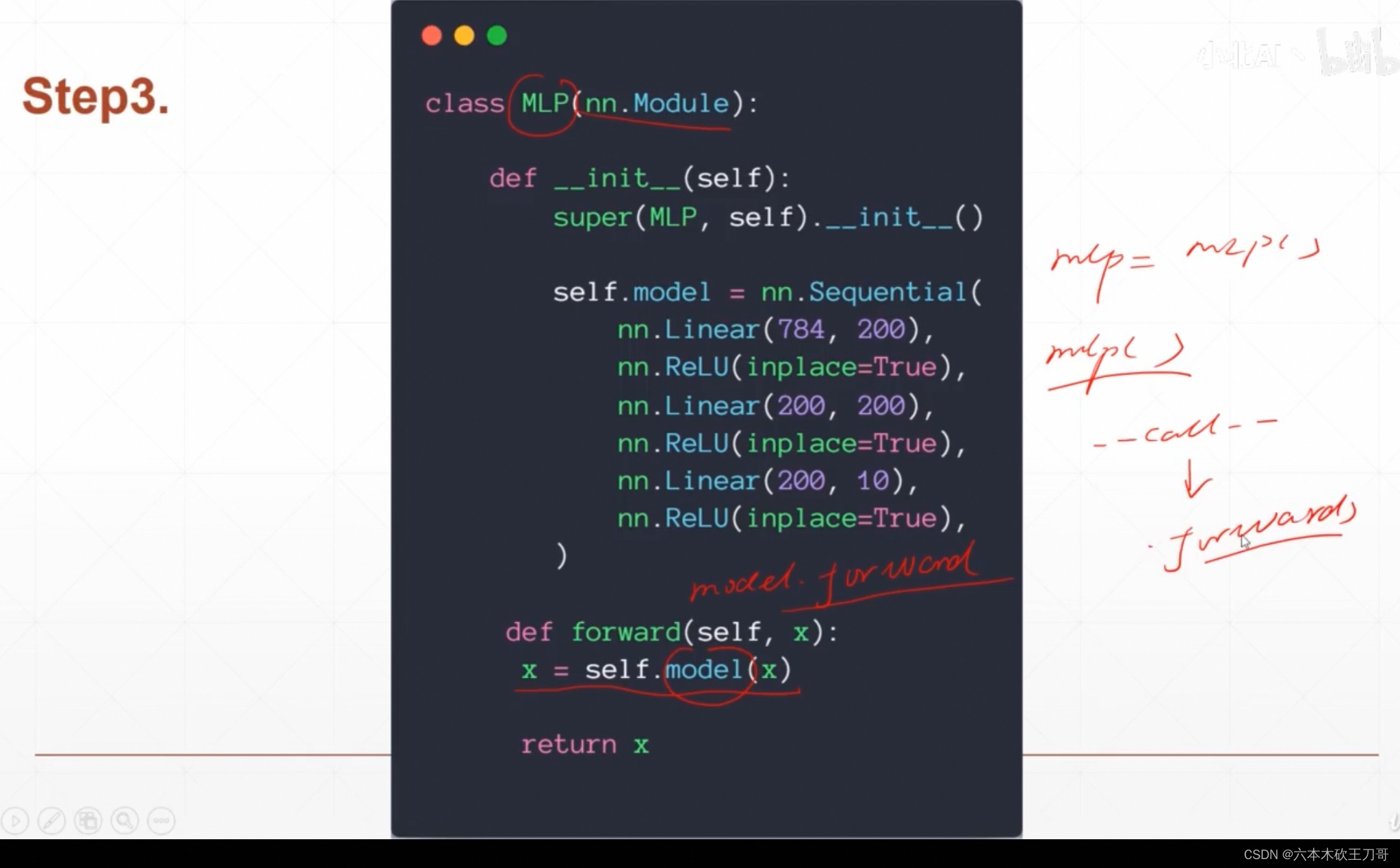
继承自nn Module的魔法，初始化一个MLP的实例，然后直接调用它就可以调用__call__，就有forward被调用。

两种relu的区别

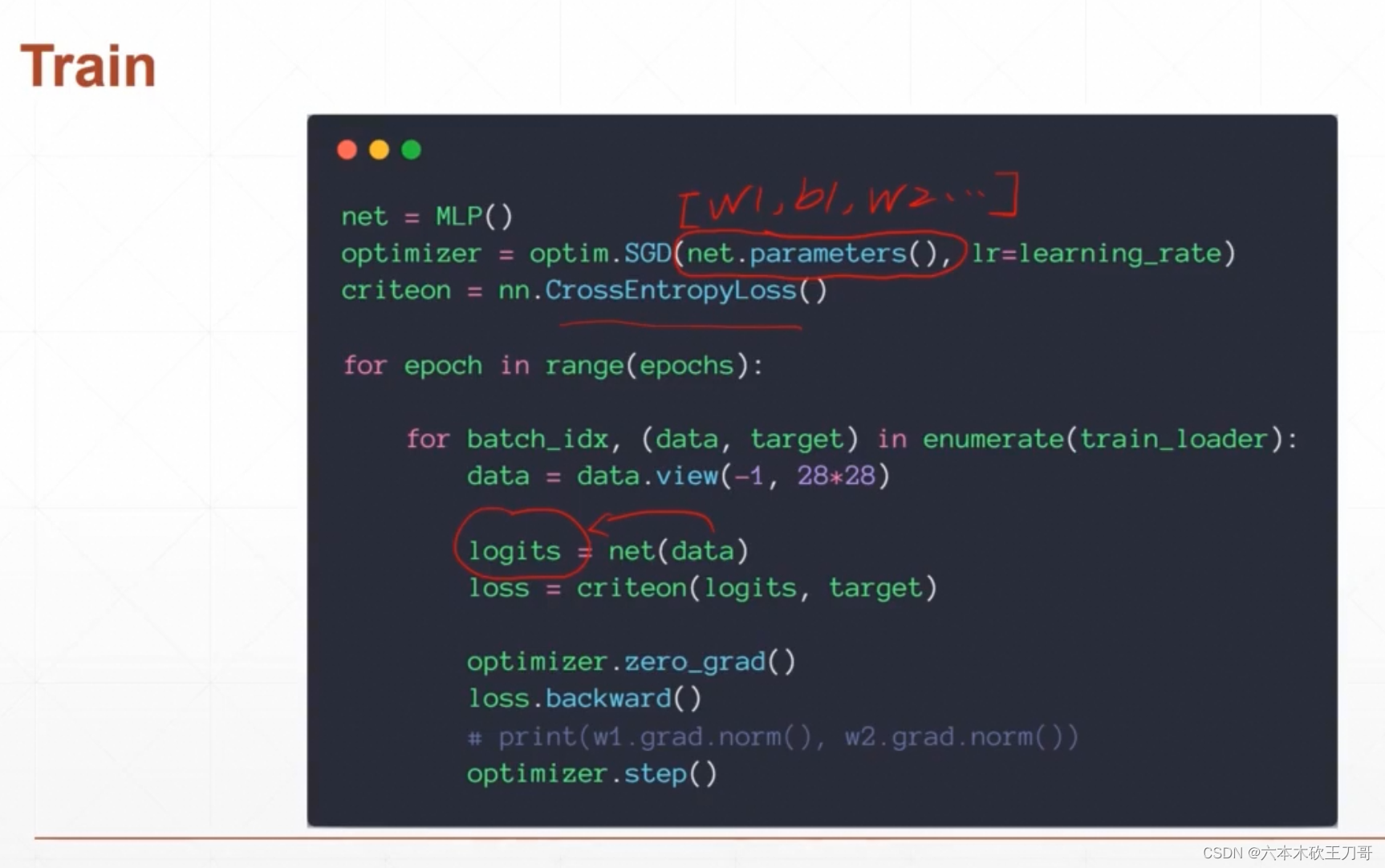
修改之前的训练代码

修改后的完整代码：

import  torch
import  torch.nn as nn
import  torch.nn.functional as F
import  torch.optim as optim
from    torchvision import datasets, transforms


batch_size=200
learning_rate=0.01
epochs=10

train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, transform=transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize((0.1307,), (0.3081,))
    ])),
    batch_size=batch_size, shuffle=True)



class MLP(nn.Module):

    def __init__(self):
        super(MLP, self).__init__()

        self.model = nn.Sequential(
            nn.Linear(784, 200),
            nn.ReLU(inplace=True),
            nn.Linear(200, 200),
            nn.ReLU(inplace=True),
            nn.Linear(200, 10),
            nn.ReLU(inplace=True),
        )

    def forward(self, x):
        x = self.model(x)

        return x

net = MLP()
optimizer = optim.SGD(net.parameters(), lr=learning_rate)
criteon = nn.CrossEntropyLoss()

for epoch in range(epochs):

    for batch_idx, (data, target) in enumerate(train_loader):
        data = data.view(-1, 28*28)

        logits = net(data)
        loss = criteon(logits, target)

        optimizer.zero_grad()
        loss.backward()
        # print(w1.grad.norm(), w2.grad.norm())
        optimizer.step()

        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item()))


    test_loss = 0
    correct = 0
    for data, target in test_loader:
        data = data.view(-1, 28 * 28)
        logits = net(data)
        test_loss += criteon(logits, target).item()

        # logits维度是[200, 10]，max(1)返回最大值和其索引，这里取第一维是索引
        pred = logits.data.max(1)[1]
        correct += pred.eq(target.data).sum()

    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

7.激活函数和GPU

Sigmoid和Tanh会遇到梯度弥散的问题，就是会出现梯度接近为0的情况。

然后ReLU函数比较常用，因为梯度大于0的时候为1，但是小于0的时候为0，所以有LeakeyReLU，SeLu和softplus激活函数来改进。

GPU加速，新版本推荐使用to(device)，注意to(device)之后的data是在GPU和CPU上不是同一个，但是网络和损失是直接搬到GPU上的

 使用GPU加速的代码如下：

import  torch
import  torch.nn as nn
import  torch.nn.functional as F
import  torch.optim as optim
from    torchvision import datasets, transforms


batch_size=200
learning_rate=0.01
epochs=10

train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, transform=transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize((0.1307,), (0.3081,))
    ])),
    batch_size=batch_size, shuffle=True)


class MLP(nn.Module):

    def __init__(self):
        super(MLP, self).__init__()

        self.model = nn.Sequential(
            nn.Linear(784, 200),
            nn.LeakyReLU(inplace=True),
            nn.Linear(200, 200),
            nn.LeakyReLU(inplace=True),
            nn.Linear(200, 10),
            nn.LeakyReLU(inplace=True),
        )

    def forward(self, x):
        x = self.model(x)

        return x

device = torch.device('cuda:0')
print(device) # cuda:0
net = MLP().to(device)
optimizer = optim.SGD(net.parameters(), lr=learning_rate)
criteon = nn.CrossEntropyLoss().to(device)

for epoch in range(epochs):

    for batch_idx, (data, target) in enumerate(train_loader):
        data = data.view(-1, 28*28)
        data, target = data.to(device), target.cuda()

        logits = net(data)
        loss = criteon(logits, target)

        optimizer.zero_grad()
        loss.backward()
        # print(w1.grad.norm(), w2.grad.norm())
        optimizer.step()

        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item()))


    test_loss = 0
    correct = 0
    for data, target in test_loader:
        data = data.view(-1, 28 * 28)
        data, target = data.to(device), target.cuda()
        logits = net(data)
        test_loss += criteon(logits, target).item()

        pred = logits.data.max(1)[1]
        correct += pred.eq(target.data).sum()

    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

8.测试方法

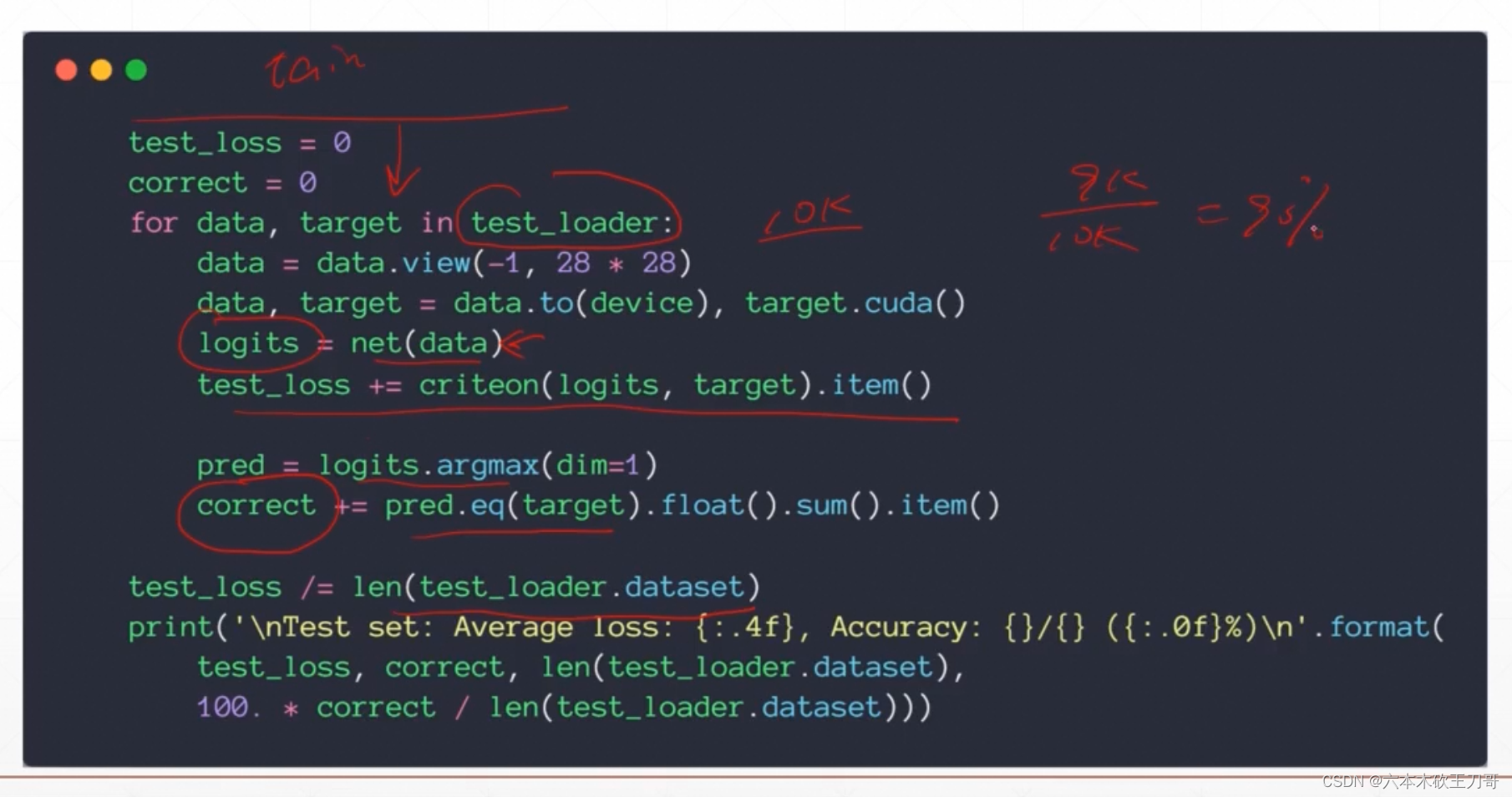
在训练过程中可能会过拟合overfiting，泛化能力会变弱，解决方法是验证。

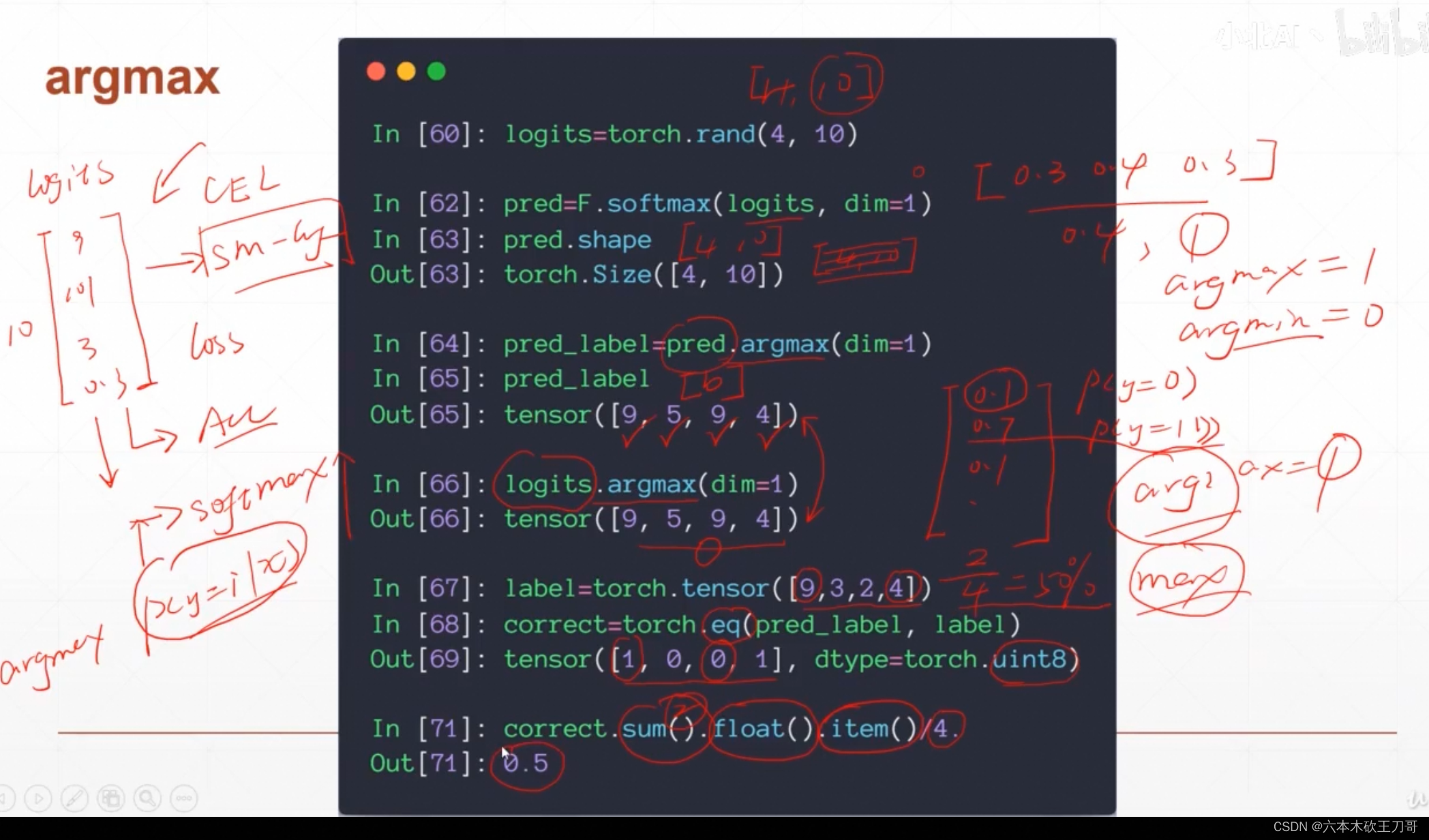
下面给了一个识别图片分类的验证例子，假设4张图片，每张图片会有10个分类，argmax就是找出一个列表里最大值的索引，给出一个label，最后得到预测正确图片的比例。

一般epoch之后再test

增加测试方法后的代码（其实和之前一样都有测试）：

import  torch
import  torch.nn as nn
import  torch.nn.functional as F
import  torch.optim as optim
from    torchvision import datasets, transforms


batch_size=200
learning_rate=0.01
epochs=10

train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, transform=transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize((0.1307,), (0.3081,))
    ])),
    batch_size=batch_size, shuffle=True)



class MLP(nn.Module):

    def __init__(self):
        super(MLP, self).__init__()

        self.model = nn.Sequential(
            nn.Linear(784, 200),
            nn.LeakyReLU(inplace=True),
            nn.Linear(200, 200),
            nn.LeakyReLU(inplace=True),
            nn.Linear(200, 10),
            nn.LeakyReLU(inplace=True),
        )

    def forward(self, x):
        x = self.model(x)

        return x

device = torch.device('cuda:0')
net = MLP().to(device)
optimizer = optim.SGD(net.parameters(), lr=learning_rate)
criteon = nn.CrossEntropyLoss().to(device)

for epoch in range(epochs):

    for batch_idx, (data, target) in enumerate(train_loader):
        data = data.view(-1, 28*28)
        data, target = data.to(device), target.cuda()

        logits = net(data)
        loss = criteon(logits, target)

        optimizer.zero_grad()
        loss.backward()
        # print(w1.grad.norm(), w2.grad.norm())
        optimizer.step()

        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item()))


    test_loss = 0
    correct = 0
    for data, target in test_loader:
        data = data.view(-1, 28 * 28)
        data, target = data.to(device), target.cuda()
        logits = net(data)
        test_loss += criteon(logits, target).item()

        pred = logits.argmax(dim=1)
        correct += pred.eq(target).float().sum().item()

    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

9. 过拟合，欠拟合和交叉验证

使用交叉验证减轻过拟合和欠拟合

如果是验证集和测试集只有一个的话，是为了验证，挑选模型参数，防止过拟合。

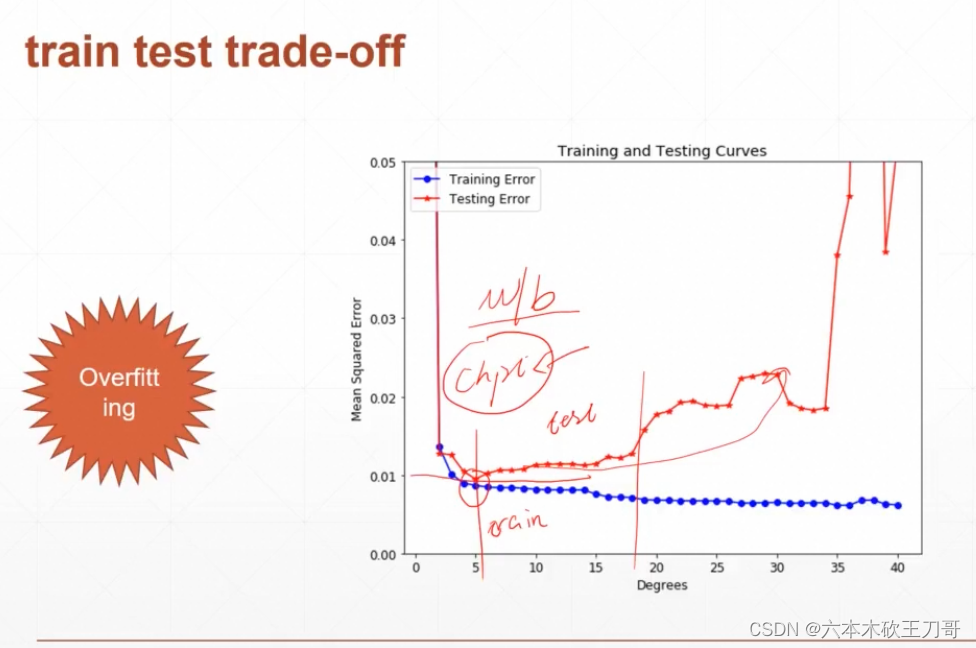
例如下面这种过拟合状态，train的loss一直在下降，但是test的error却异常上升，此时需要在每个epoch检查一次，然后在确定过拟合的时候挑选保存checkpoint（当前的w/b参数）后停止训练。

如果这时候有三种数据集：训练集，验证集和测试集，测试挑选和保存checkpoint的任务就交给验证集了，此时验证集上也要保证模型性能够好，然后才能选出最终的参数，所以此时测试集的作用就是交给“客户”去测试模型的性能，而不是用验证集（因为验证集已经得到了不错的性能） 。

具体划分三种数据集的代码：

K-fold验证，轮流用数据做训练集和验证集。

 相关代码：

import  torch
import  torch.nn as nn
import  torch.nn.functional as F
import  torch.optim as optim
from    torchvision import datasets, transforms


batch_size=200
learning_rate=0.01
epochs=10

train_db = datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ]))
train_loader = torch.utils.data.DataLoader(
    train_db,
    batch_size=batch_size, shuffle=True)

test_db = datasets.MNIST('../data', train=False, transform=transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307,), (0.3081,))
]))
test_loader = torch.utils.data.DataLoader(test_db,
    batch_size=batch_size, shuffle=True)


print('train:', len(train_db), 'test:', len(test_db))
train_db, val_db = torch.utils.data.random_split(train_db, [50000, 10000])
print('db1:', len(train_db), 'db2:', len(val_db))
train_loader = torch.utils.data.DataLoader(
    train_db,
    batch_size=batch_size, shuffle=True)
val_loader = torch.utils.data.DataLoader(
    val_db,
    batch_size=batch_size, shuffle=True)




class MLP(nn.Module):

    def __init__(self):
        super(MLP, self).__init__()

        self.model = nn.Sequential(
            nn.Linear(784, 200),
            nn.LeakyReLU(inplace=True),
            nn.Linear(200, 200),
            nn.LeakyReLU(inplace=True),
            nn.Linear(200, 10),
            nn.LeakyReLU(inplace=True),
        )

    def forward(self, x):
        x = self.model(x)

        return x

device = torch.device('cuda:0')
net = MLP().to(device)
optimizer = optim.SGD(net.parameters(), lr=learning_rate)
criteon = nn.CrossEntropyLoss().to(device)

for epoch in range(epochs):

    for batch_idx, (data, target) in enumerate(train_loader):
        data = data.view(-1, 28*28)
        data, target = data.to(device), target.cuda()

        logits = net(data)
        loss = criteon(logits, target)

        optimizer.zero_grad()
        loss.backward()
        # print(w1.grad.norm(), w2.grad.norm())
        optimizer.step()

        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item()))


    # 这里改成了验证
    test_loss = 0
    correct = 0
    for data, target in val_loader:
        data = data.view(-1, 28 * 28)
        data, target = data.to(device), target.cuda()
        logits = net(data)
        test_loss += criteon(logits, target).item()

        pred = logits.data.max(1)[1]
        correct += pred.eq(target.data).sum()

    test_loss /= len(val_loader.dataset)
    print('\nVAL set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(val_loader.dataset),
        100. * correct / len(val_loader.dataset)))



test_loss = 0
correct = 0
for data, target in test_loader:
    data = data.view(-1, 28 * 28)
    data, target = data.to(device), target.cuda()
    logits = net(data)
    test_loss += criteon(logits, target).item()

    pred = logits.data.max(1)[1]
    correct += pred.eq(target.data).sum()

test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
    test_loss, correct, len(test_loader.dataset),
    100. * correct / len(test_loader.dataset)))

10. 正则化

下面总结几种解决过拟合的几种方法

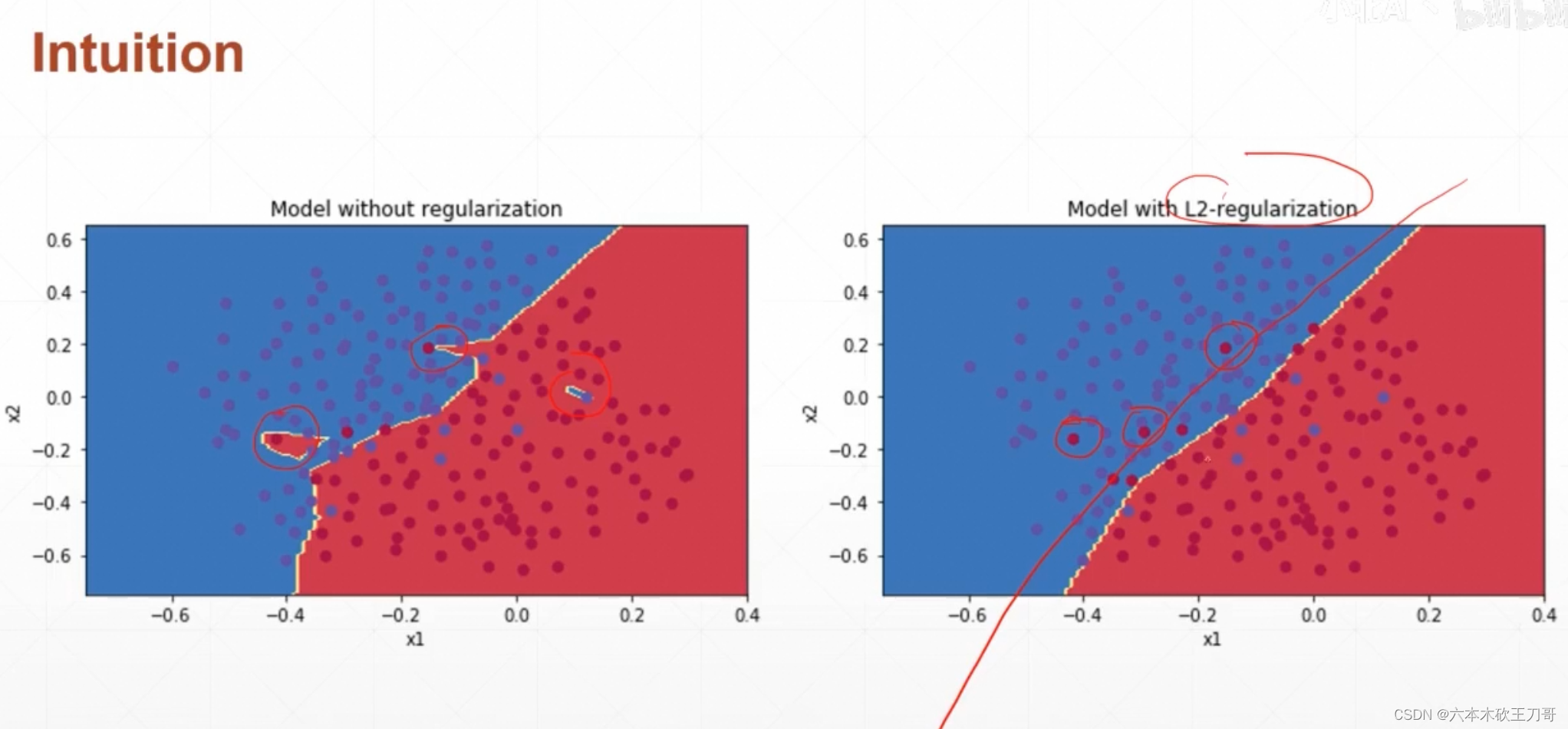
正则化就是降低模型的复杂度，比如使得某些高次项消失

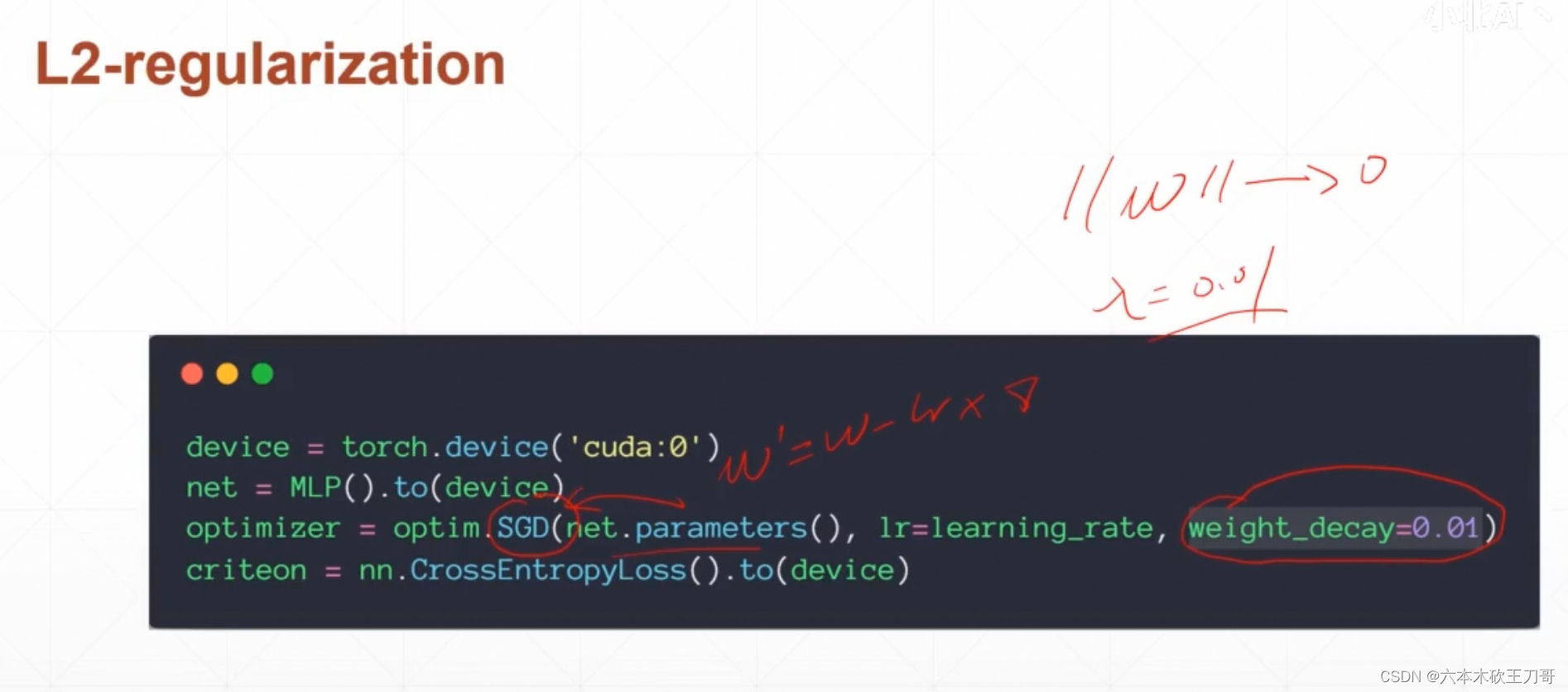
两种正则化方法

需要手写L1正则化，就是把所有w参数求和，然后乘上一个超参数0.01，最后加入到总的loss里面再反向传播更新梯度。

11. 动量与学习率

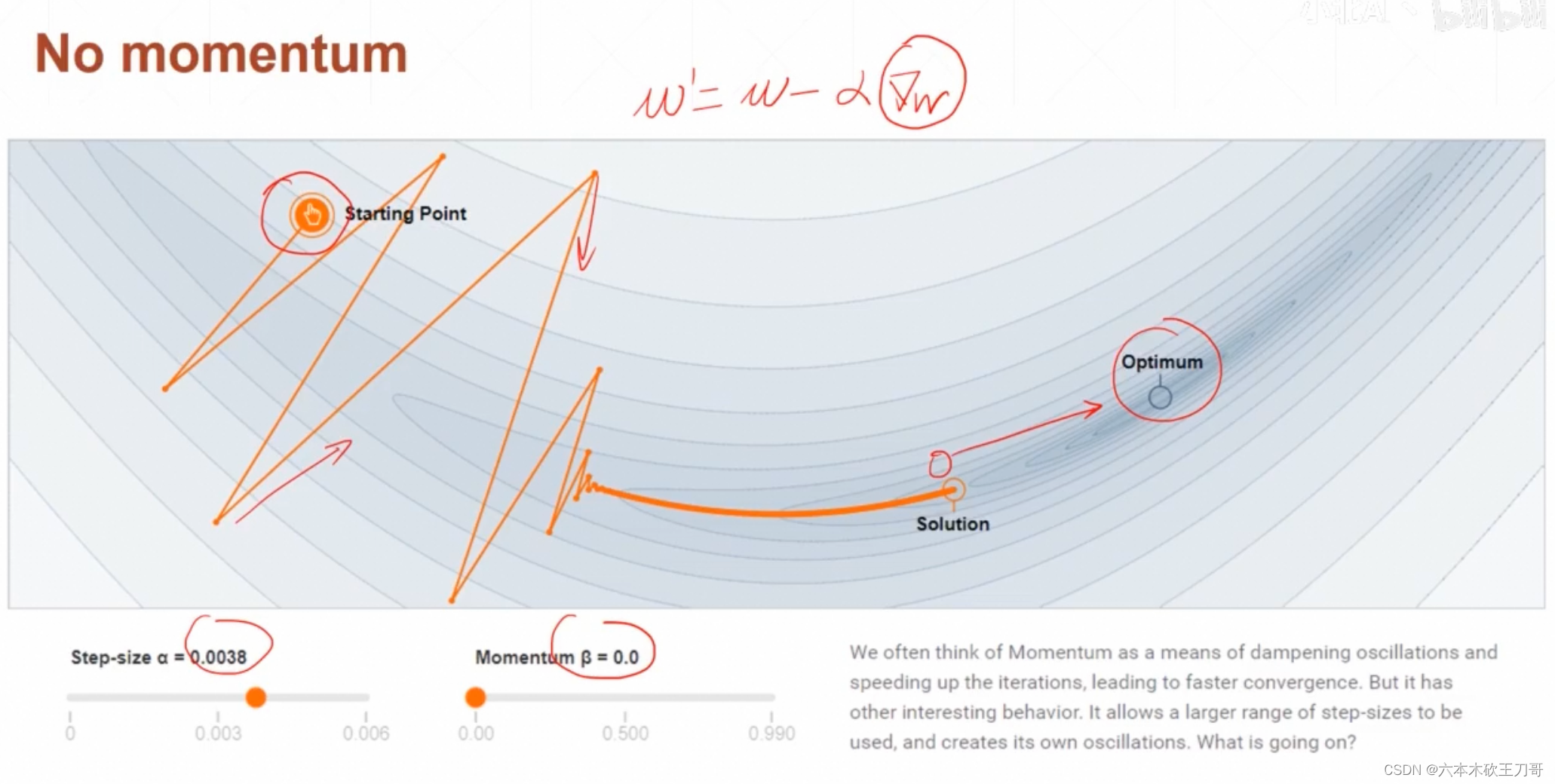
下面是增加动量之后的梯度更新规则，其中改变的zk+1其实就是zk和wk梯度之和，然后zk又与上一个梯度wk-1相关，所以动量的意义就是增加之前的一个向量方法，使得当前更新的时候可以被之前的方法影响。

举一个没有动量的例子，这里更新幅度会很大，然后无法找到最小值点

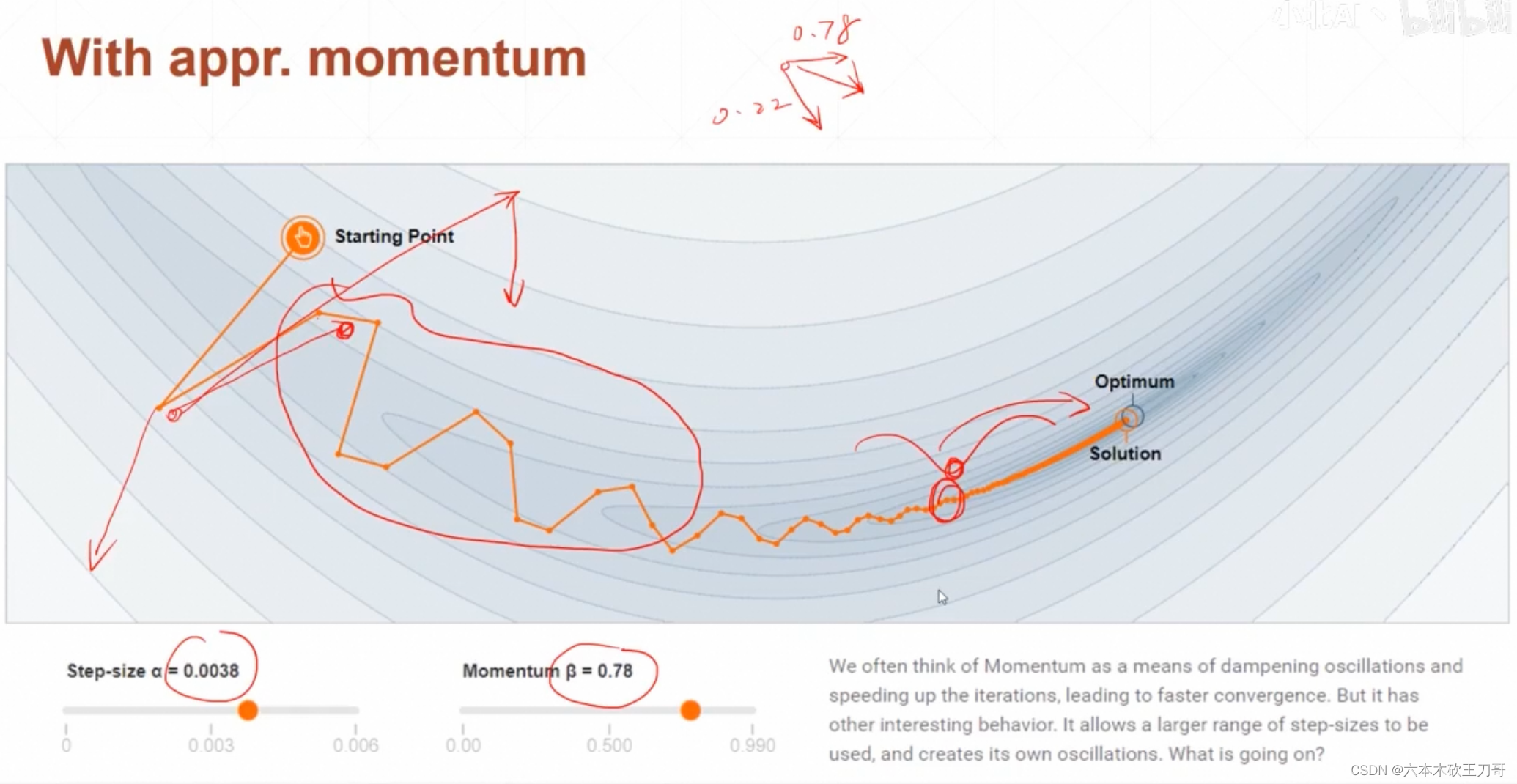
设定动量之后会发现更新的幅度没有那么大了，因为每次更新还要考虑之前的幅度。

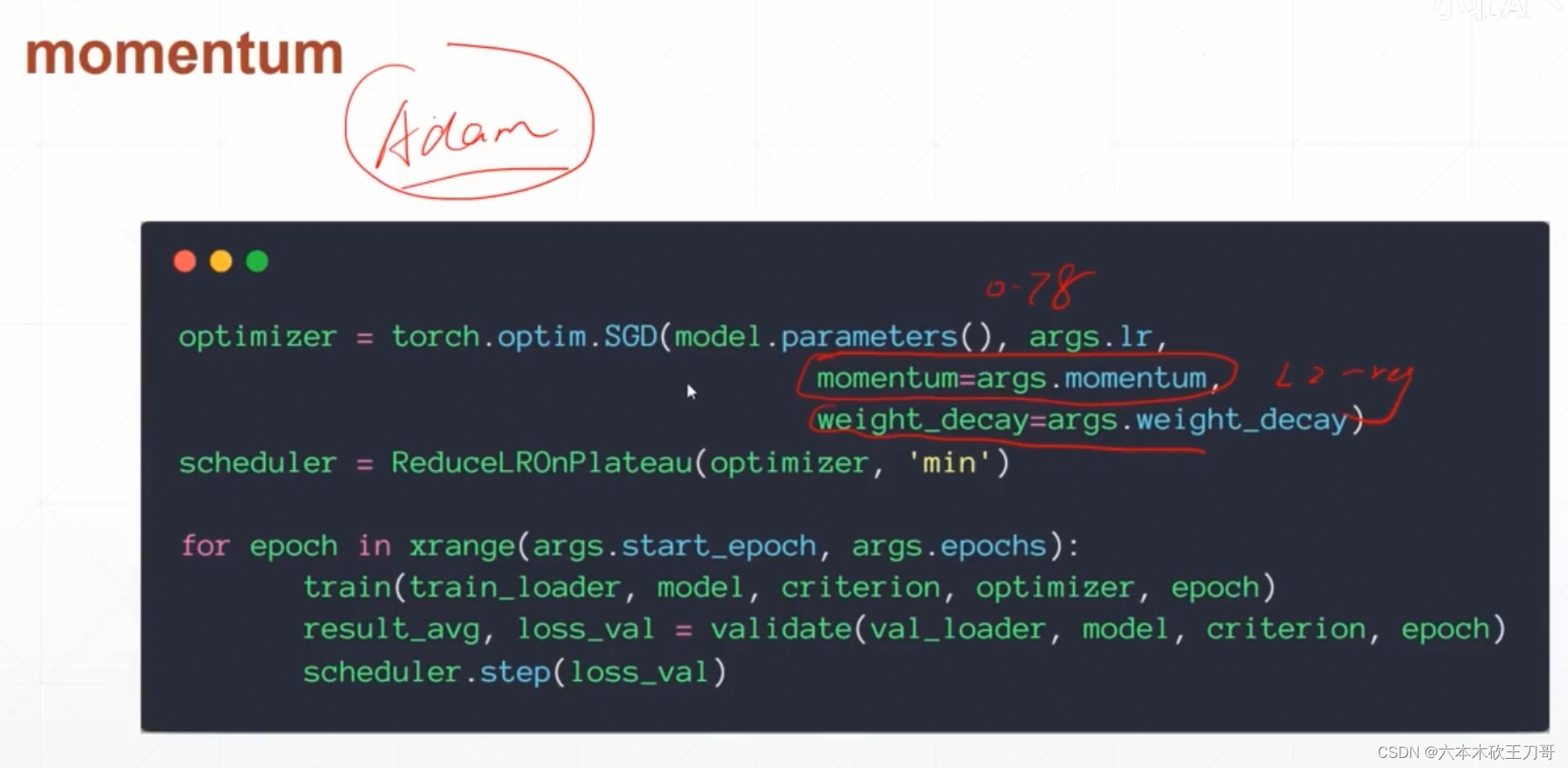
在SGD优化器中需要加上这个优化，而Adam优化自动会有

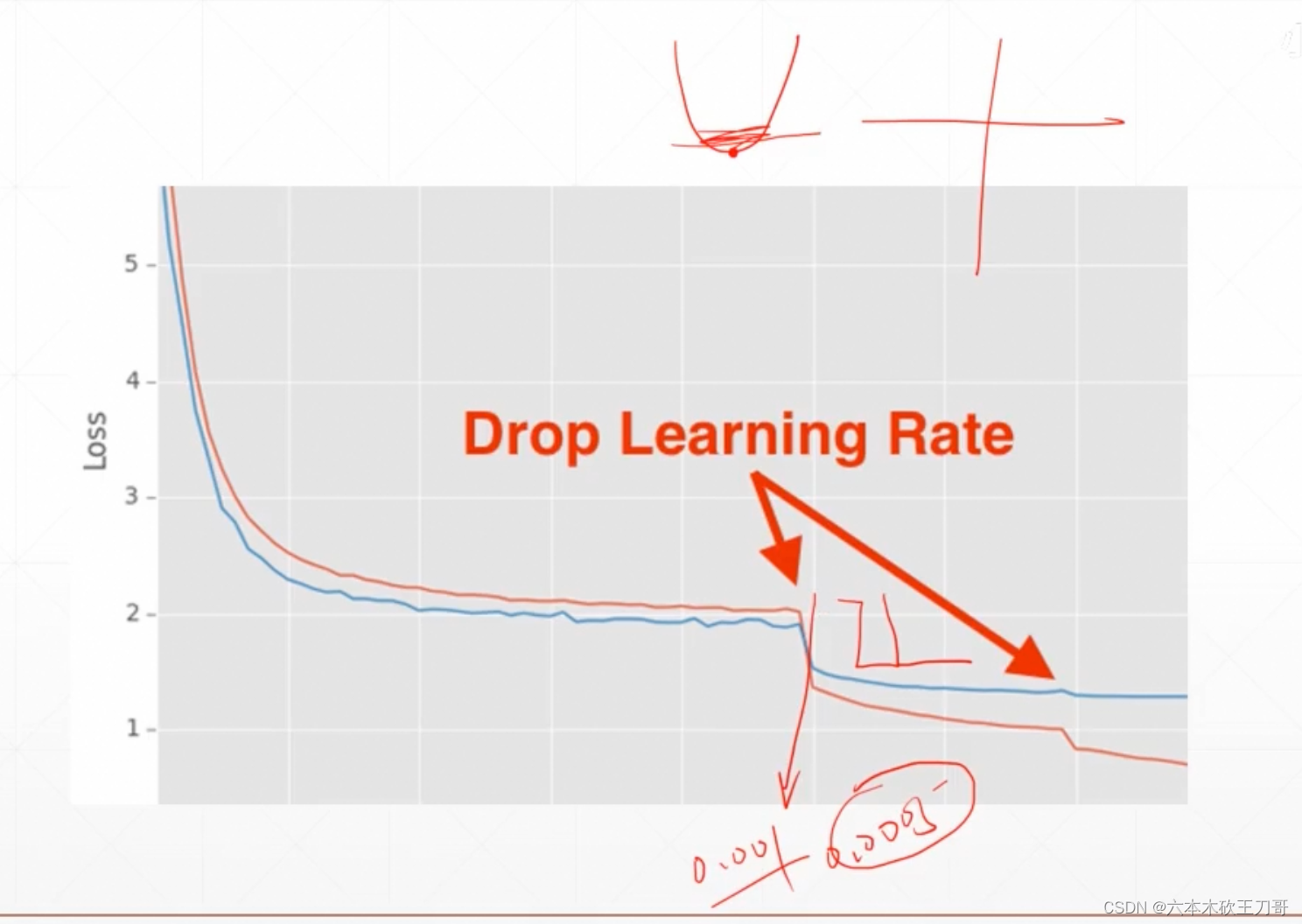
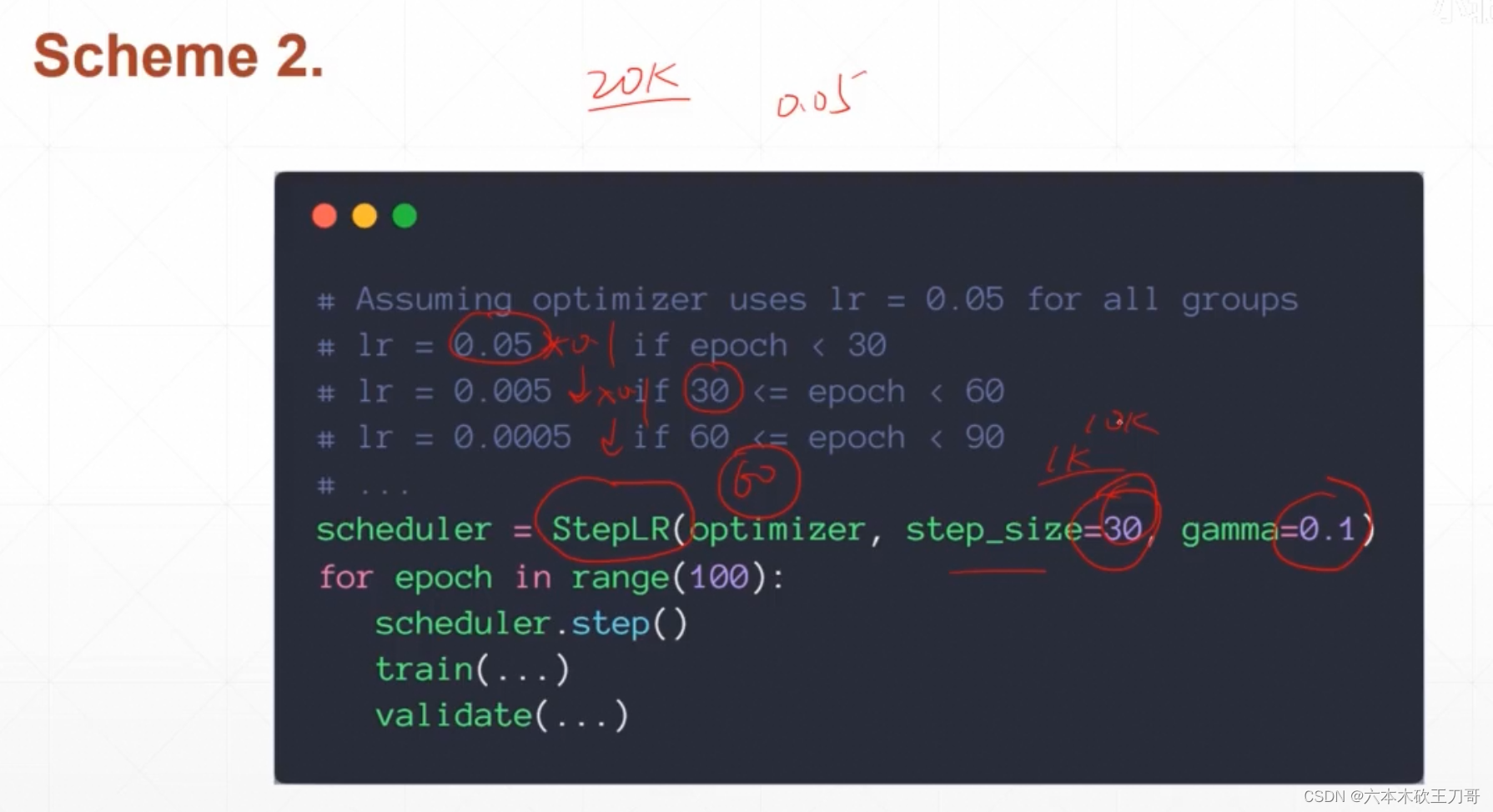
学习率微调，从略大慢慢调小

常见学习率监听方案，就是使用下面这个方法去管理学习率，然后更新学习率

还可以用别的方法自动更新学习率： 

12. Dropout

13. 卷积

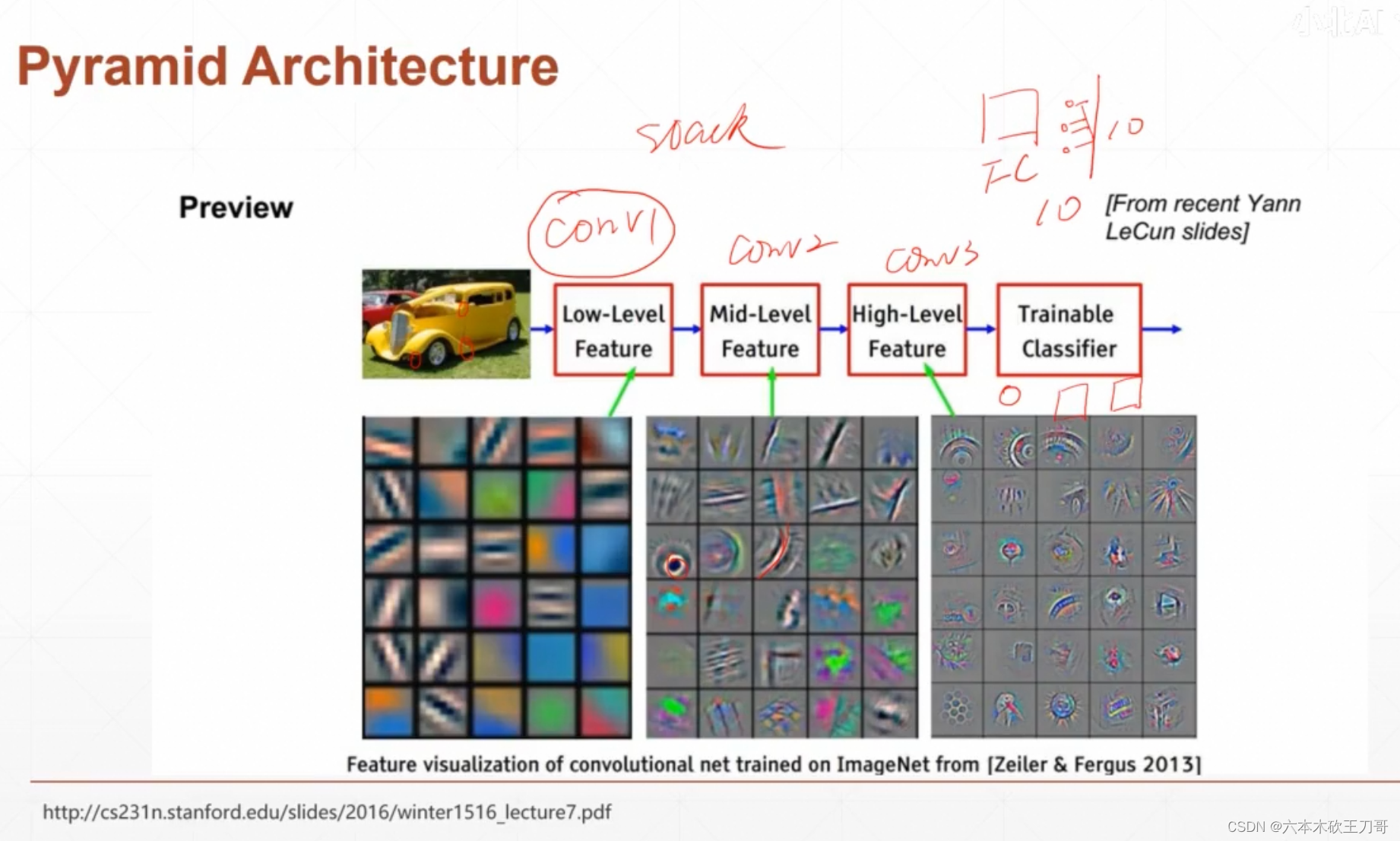
卷积层每层叠加会抽象出每层的特征，第一层是一些轮廓，第二层往后就是一些更具体的组成

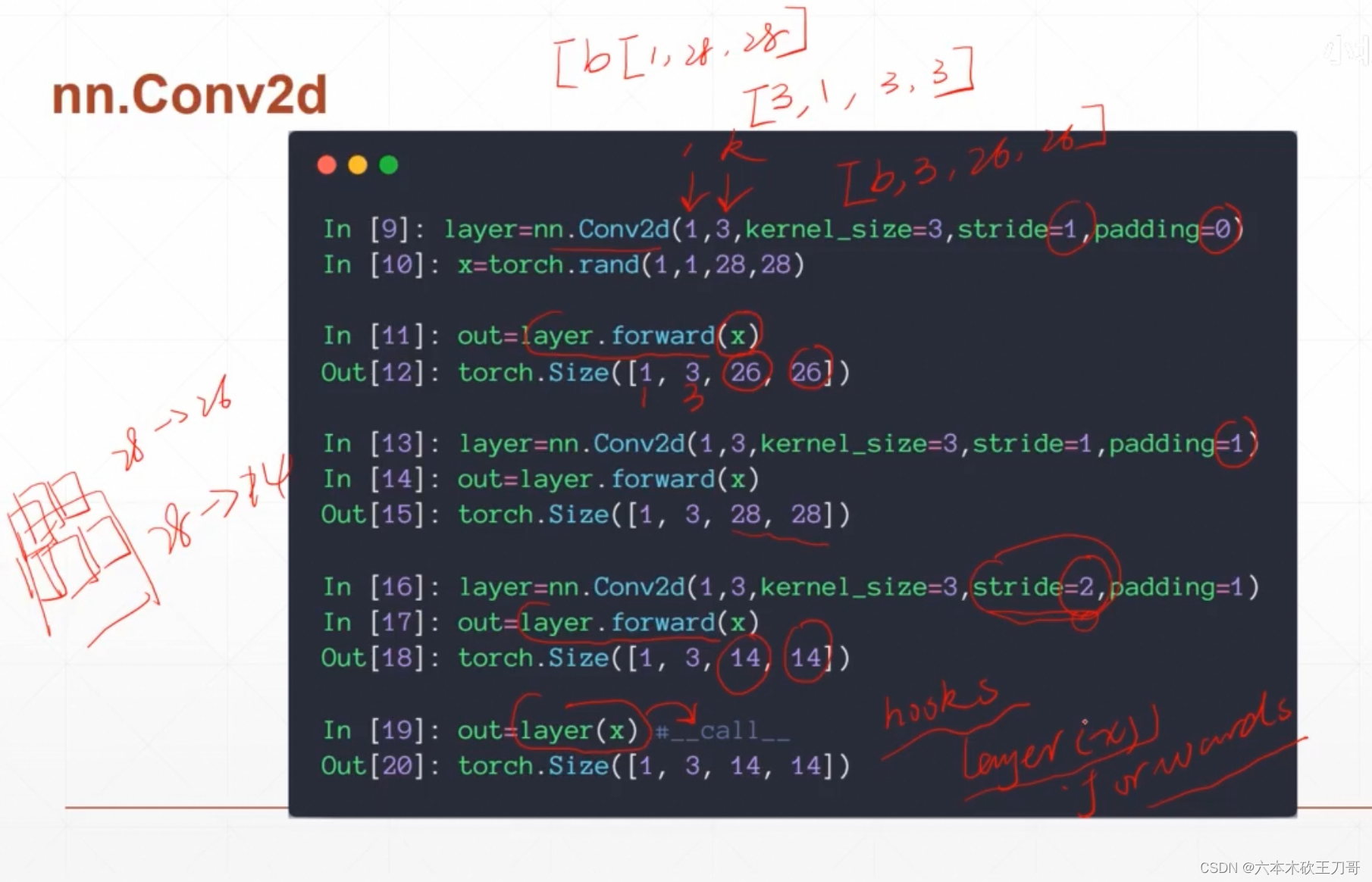
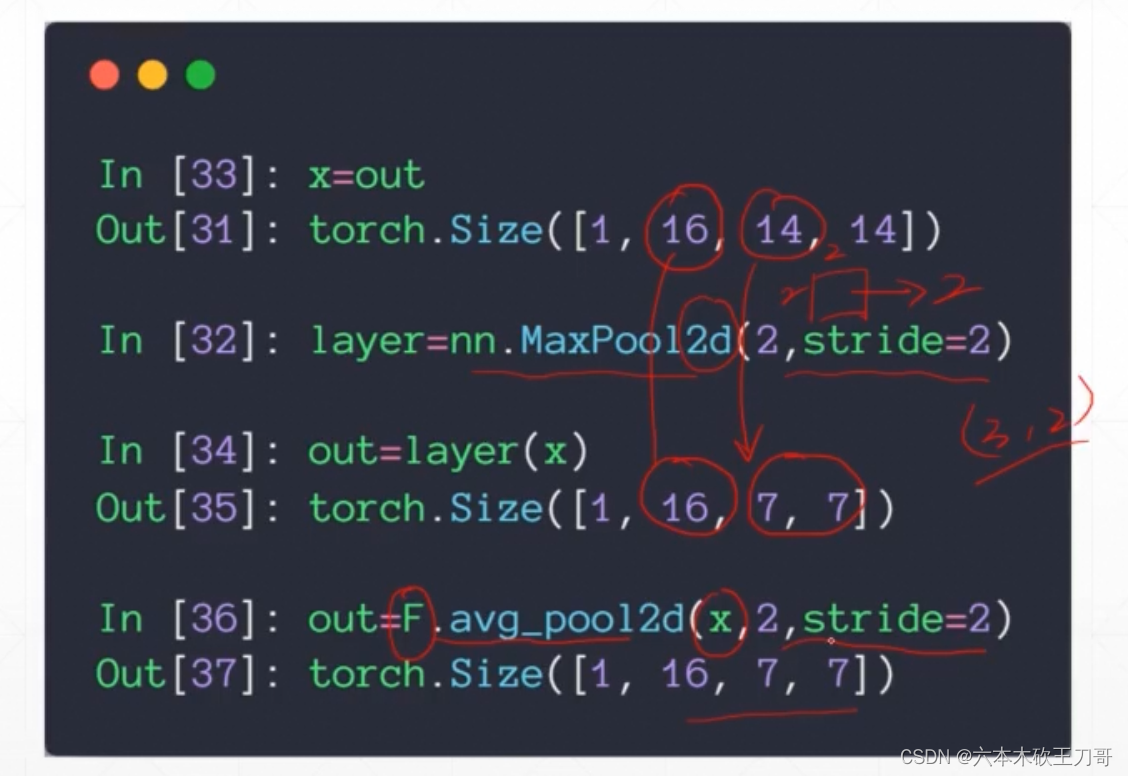
使用PyTorch构建卷积操作，Conv2d的参数第一个是图片数量，第二个是kernel数量，之后是kernel形状，以及stride和padding大小，注意当调用这个层返回的实例时，需要直接用layer+括号的形式，因为pytorch内部是直接调用call魔法函数，其中会自动进行一些hooks操作，而forward函数没法做到，除非明确只用forward函数的时候才可以。

pytorch之torch.nn.Conv2d()函数详解-CSDN博客

打印出layer的权重，可以发现这里的Size是[3, 1, 3, 3]，代表这里是3个kernel，并且每个kernel的channel是1，size是3x3，并且偏移也是3 

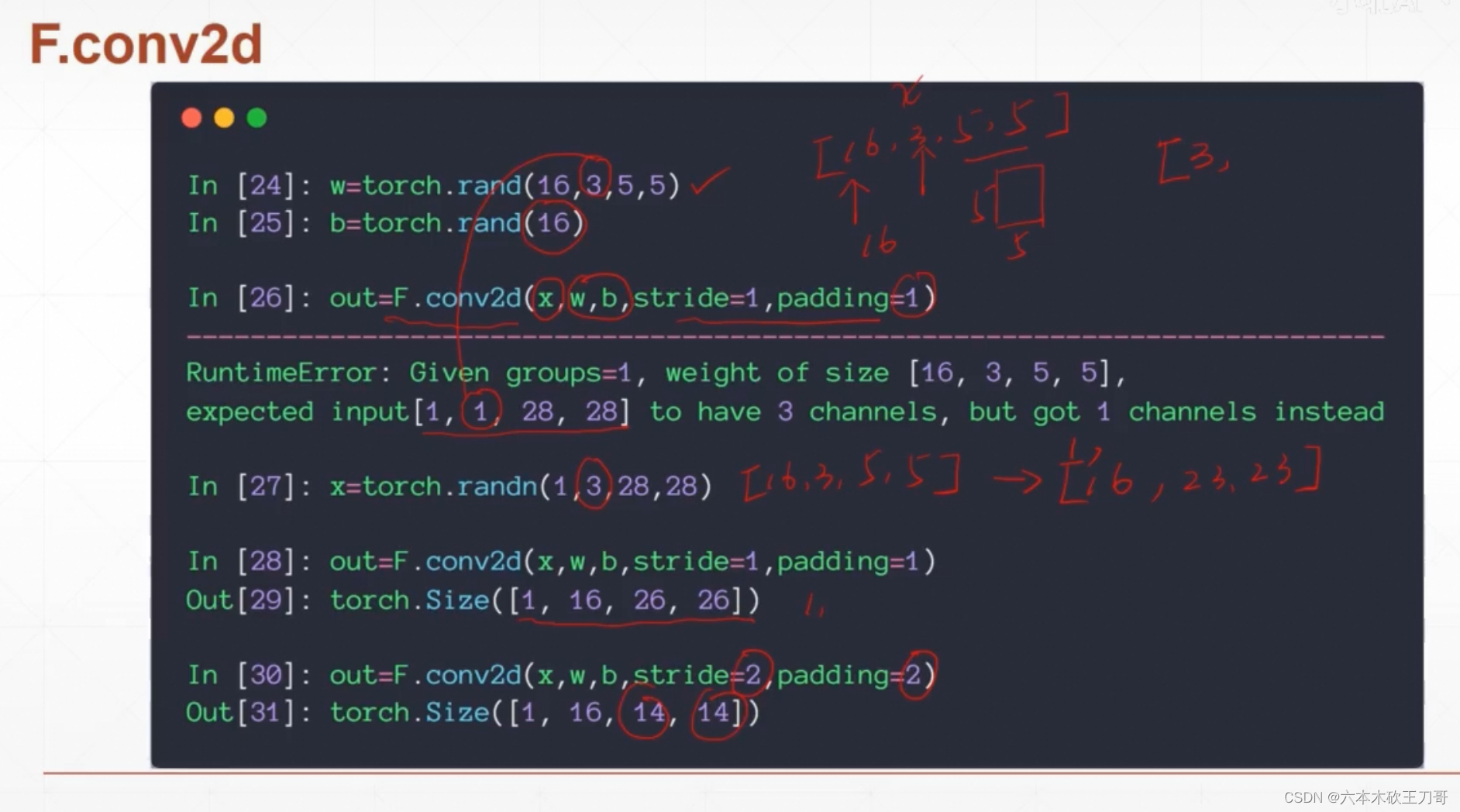
使用更底层的函数，传入的参数是w（kernel的维度），b是偏移，x是输入的图片Size，注意这里图片的channel数量和Kernel的channel数量必须一致

向下采样，降维操作：最大池化和平均池化 

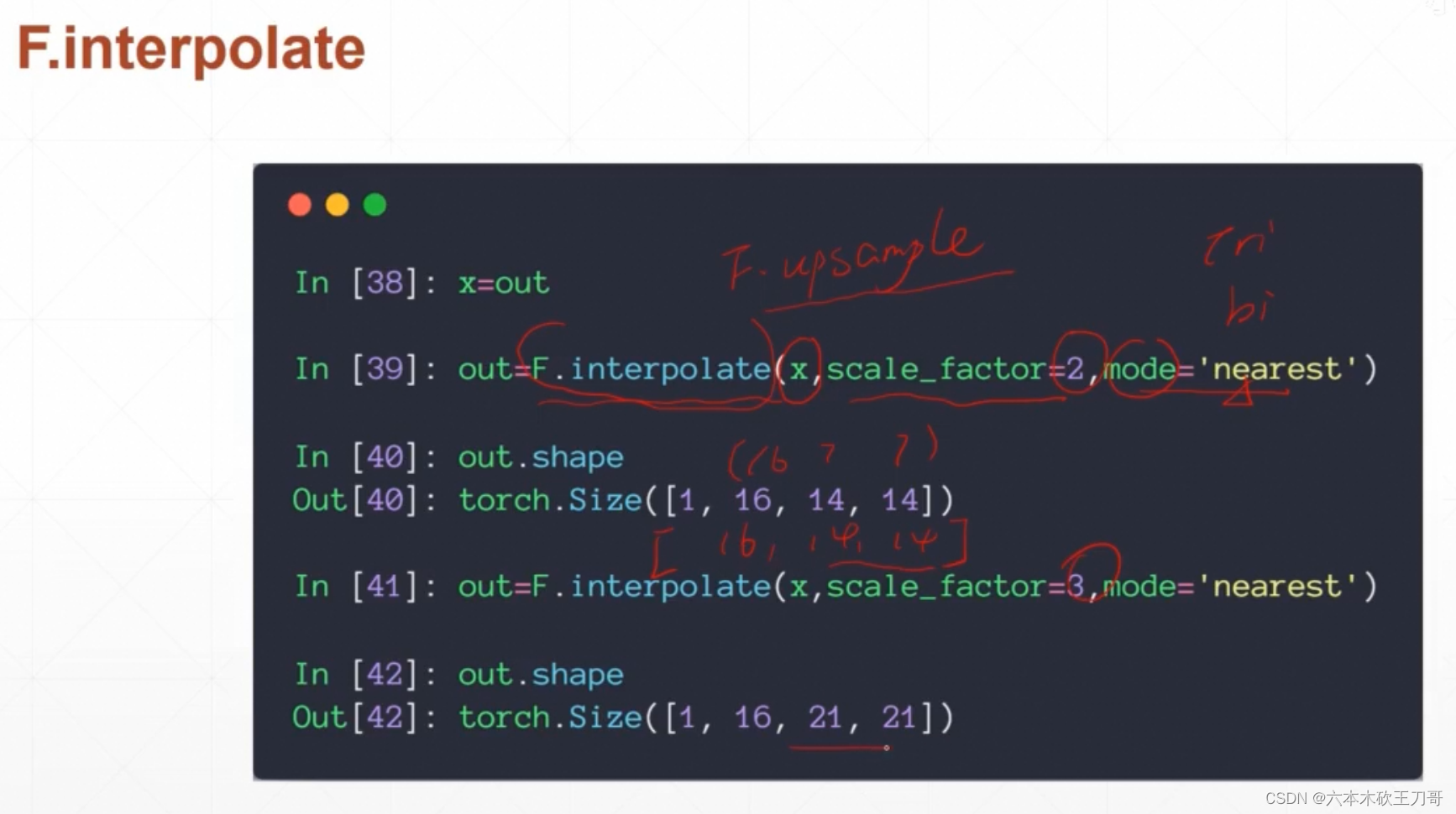
向上采样，放大图片，使用差值函数

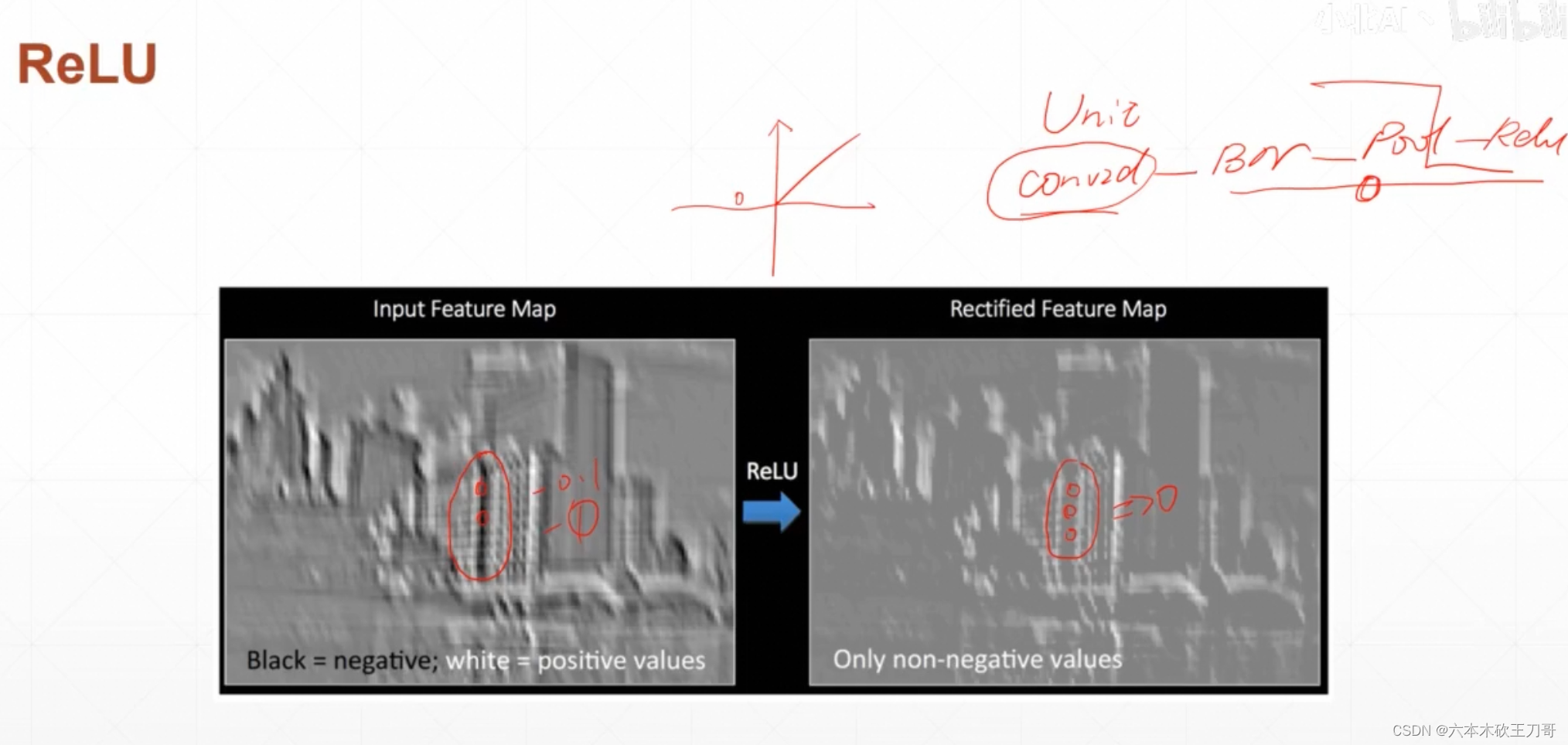
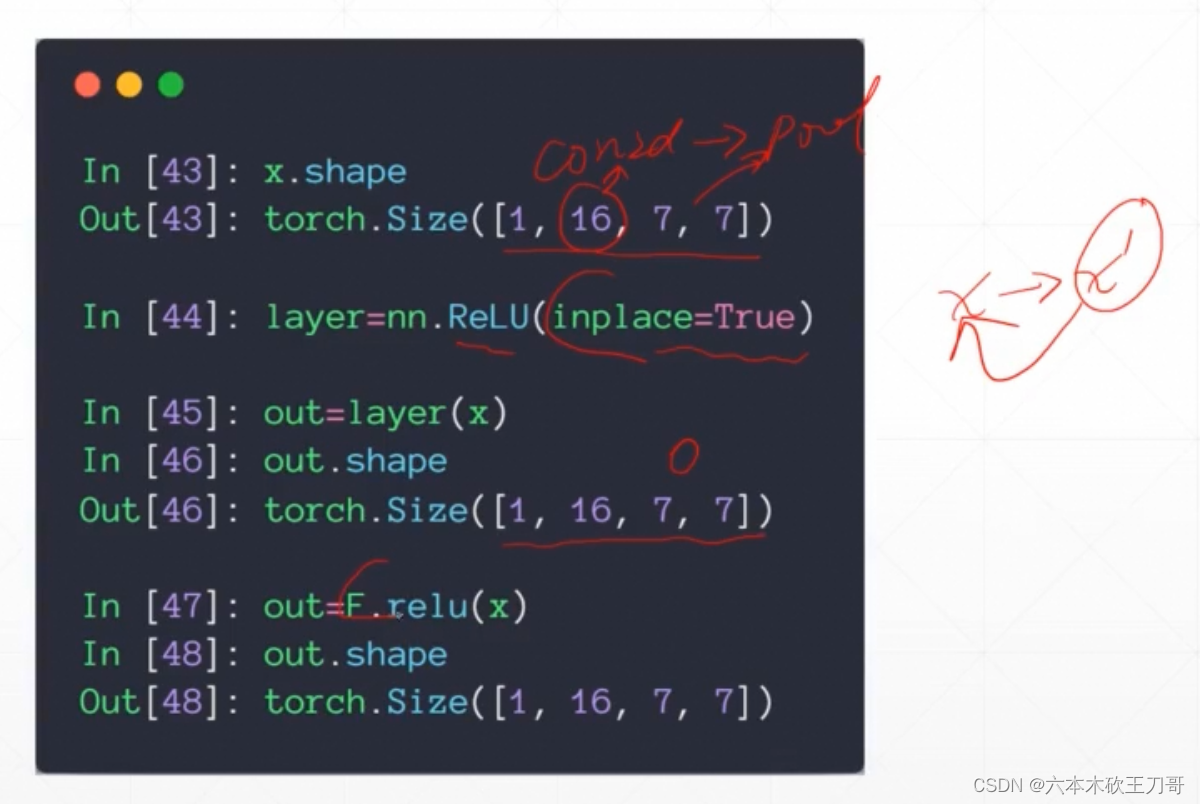
用ReLU函数去去掉一些低的响应，比如说下面黑色部分是负值经过relu会变成0

用Pytorch实现

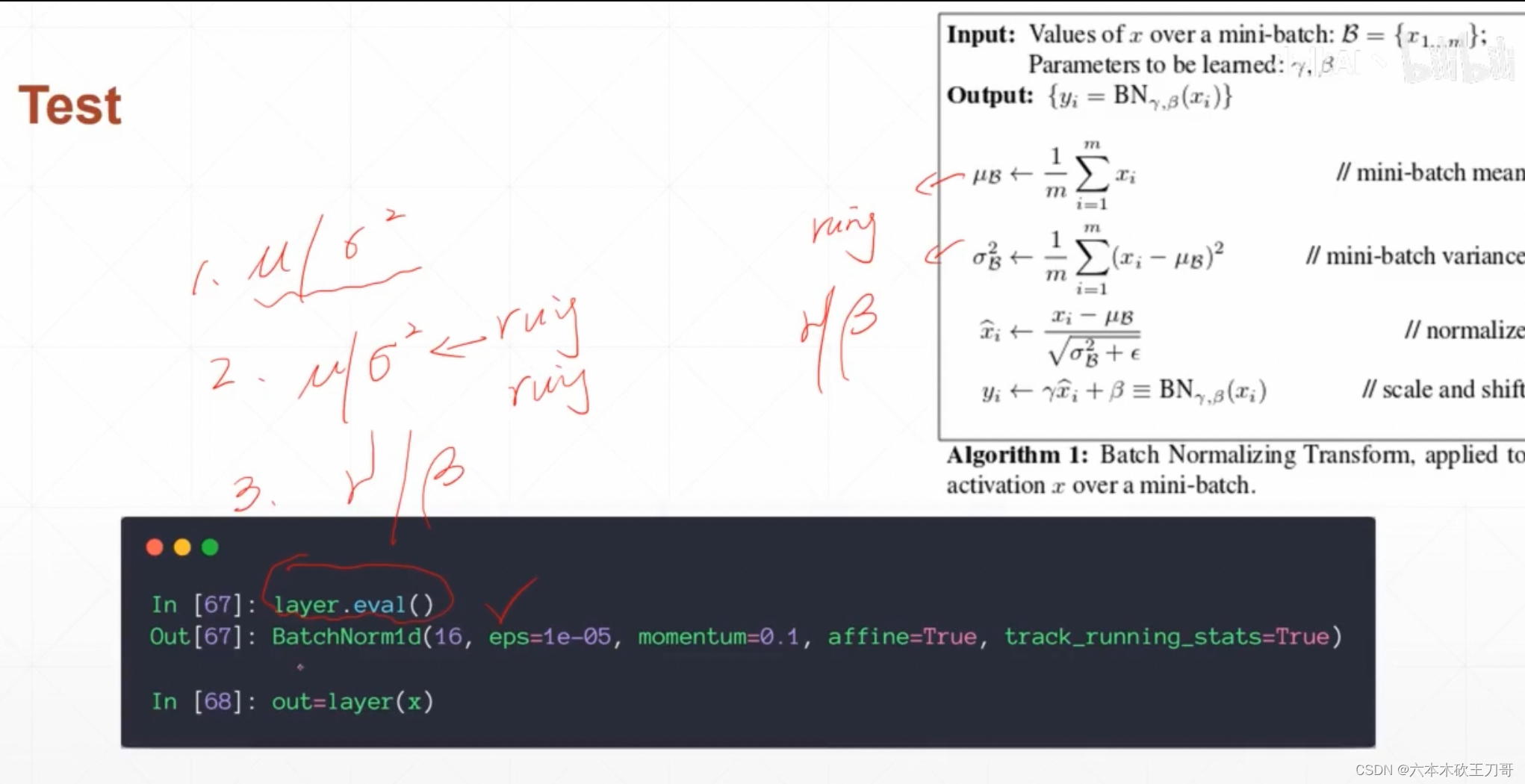
14. BatchNorm

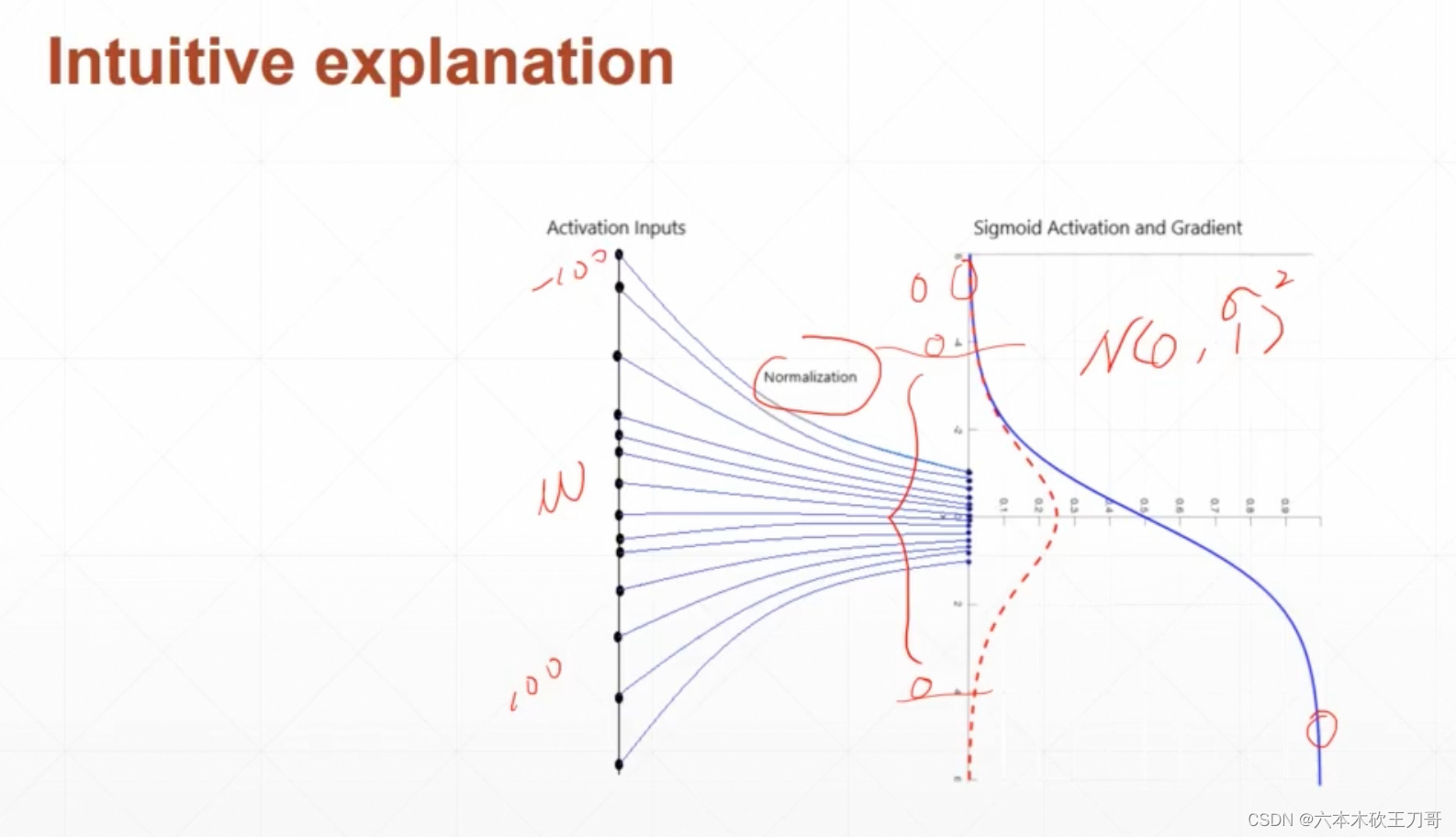
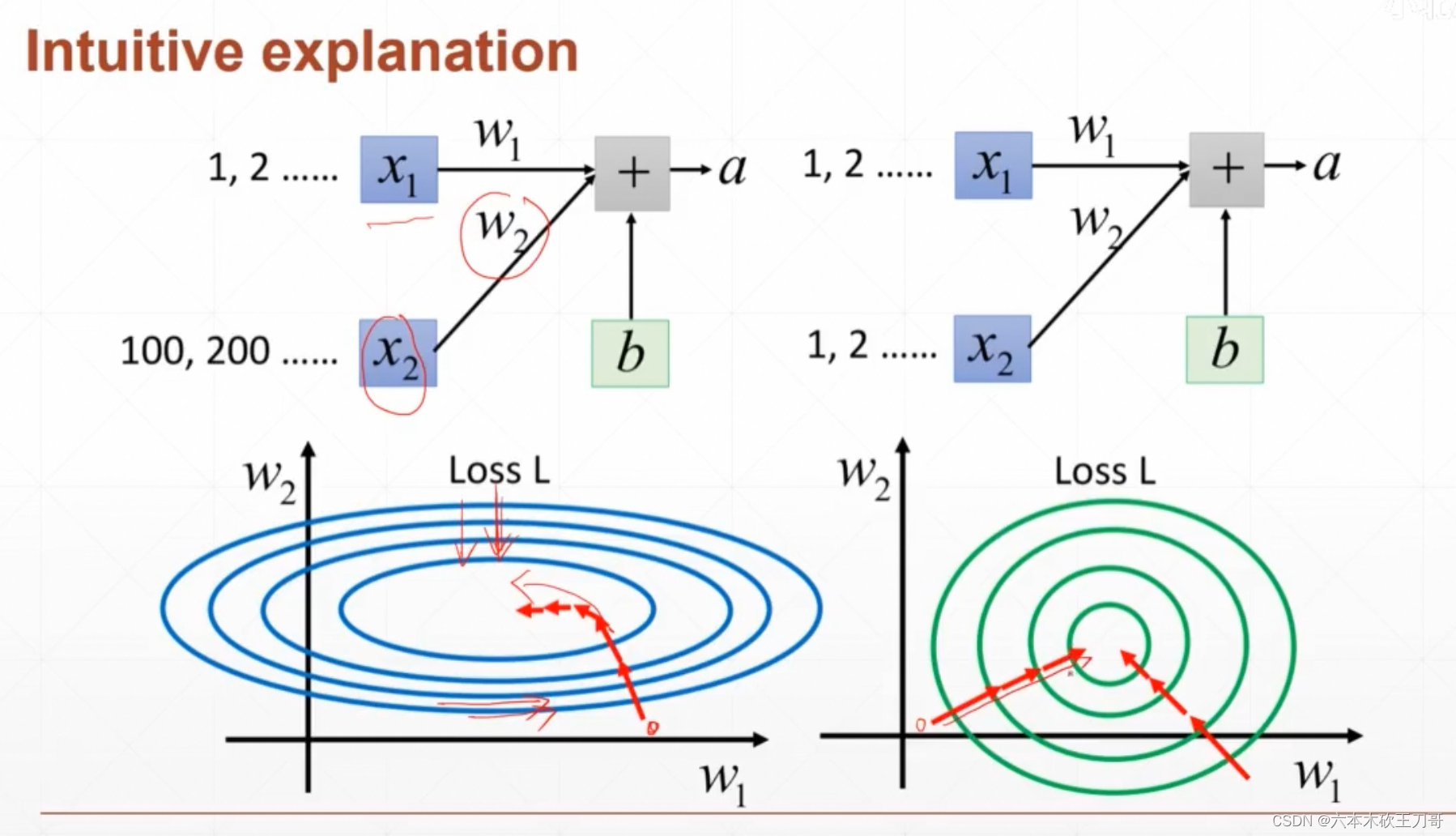
当需要输入数据到Sigmoid激活函数的时候，如果值过大或者过小，会导致出现梯度弥散的现象，所以可以使用Batchnorm来把值集中到某个区间内，比如遵守一个均值为0，方差为1的分布。

用一个直观的理解，比如某个地方输入过大，会导致那个梯度有关的方向会下降的更快，如果值比较平均的话，就不会有这种情况

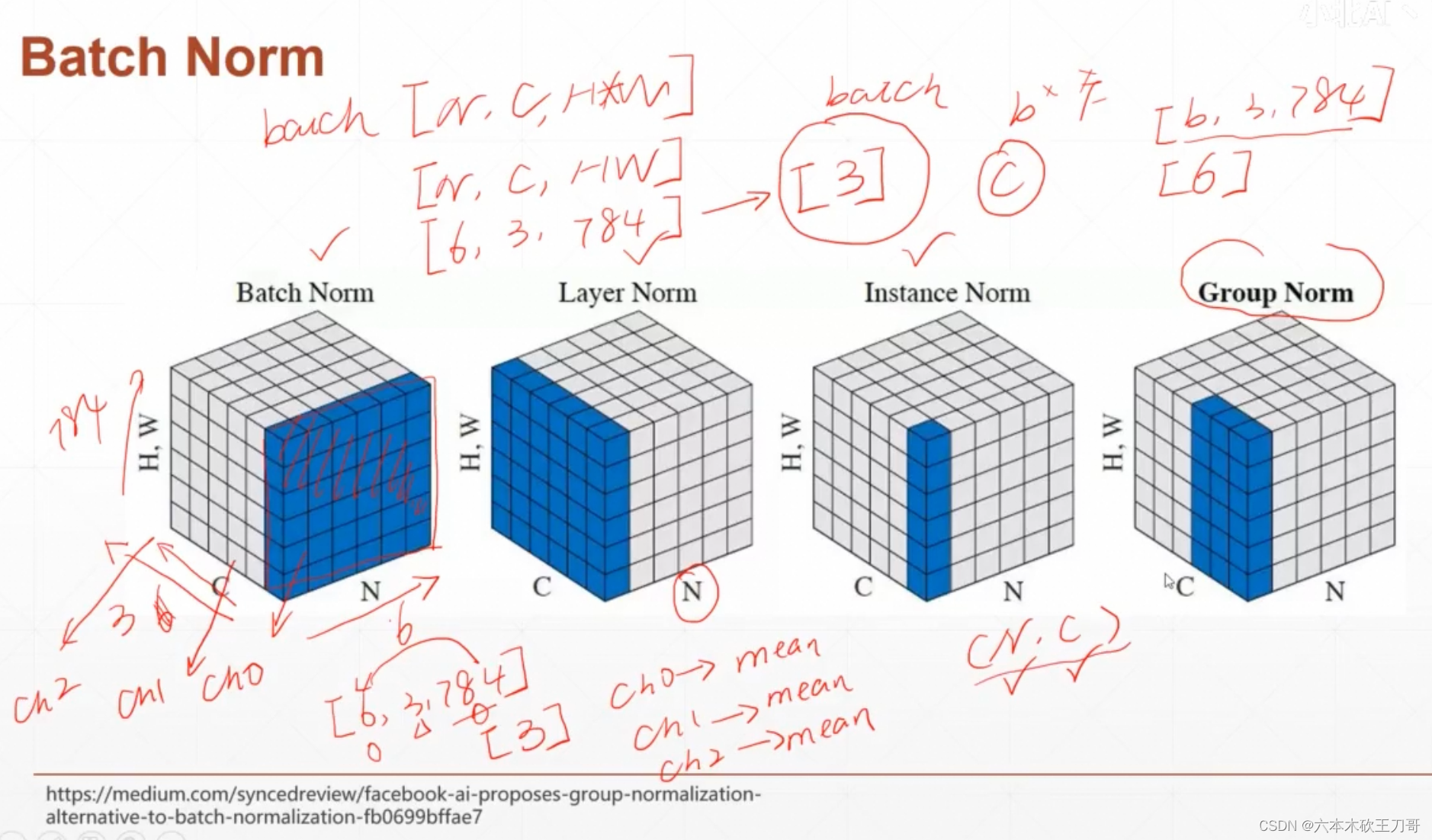
对于图片，比如是[6, 3, 784]，6张3x784的图片，然后BatchNorm是对3个channel求均值得到一个维度为1，Size为3的向量，LayerNorm是对6张图片求均值，得到一个维度为1，Size为6的向量，对于下图中蓝色部分，其实就是对应每个通道维度所有图片之和，求这个维度的均值

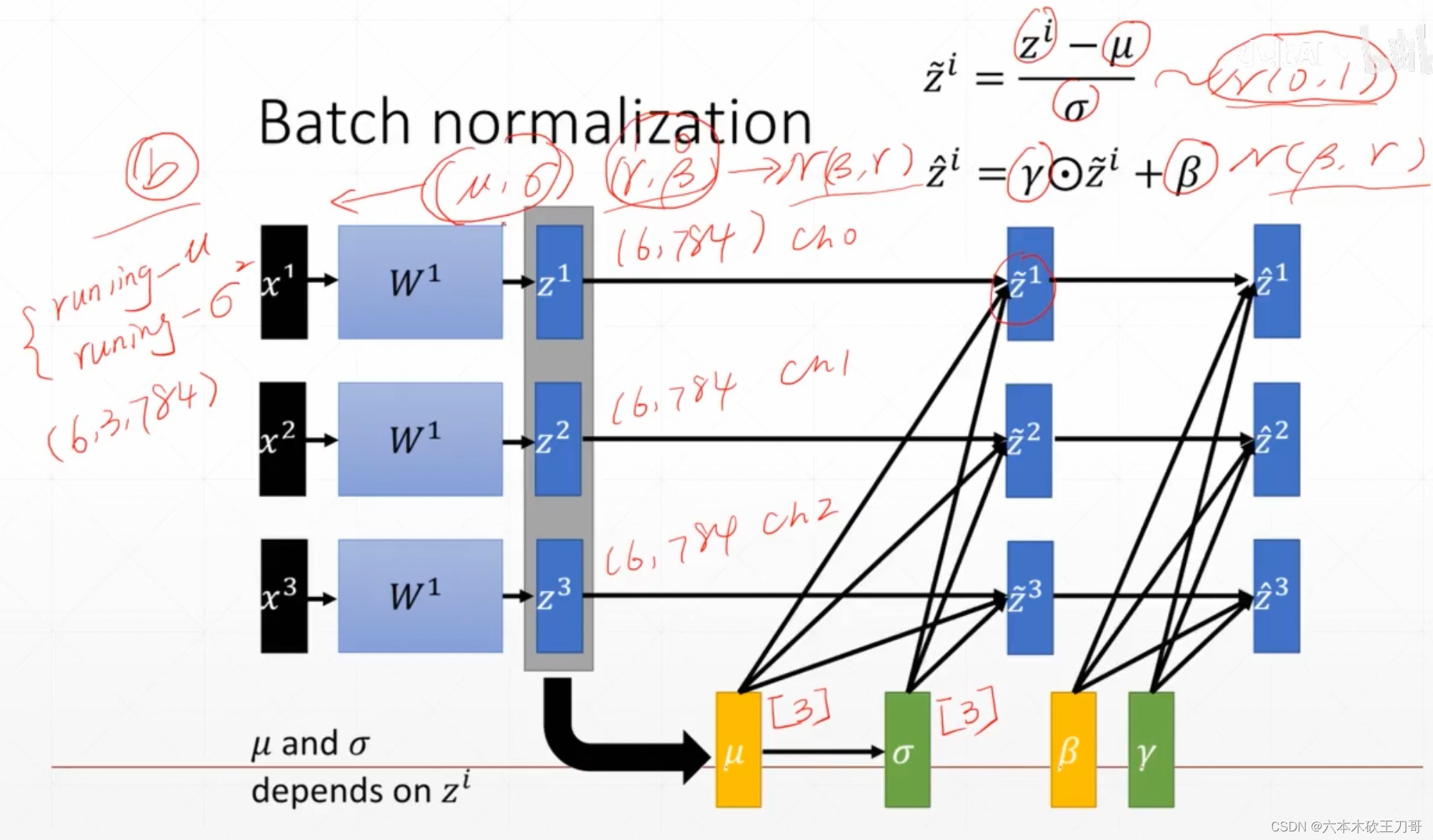
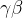
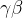
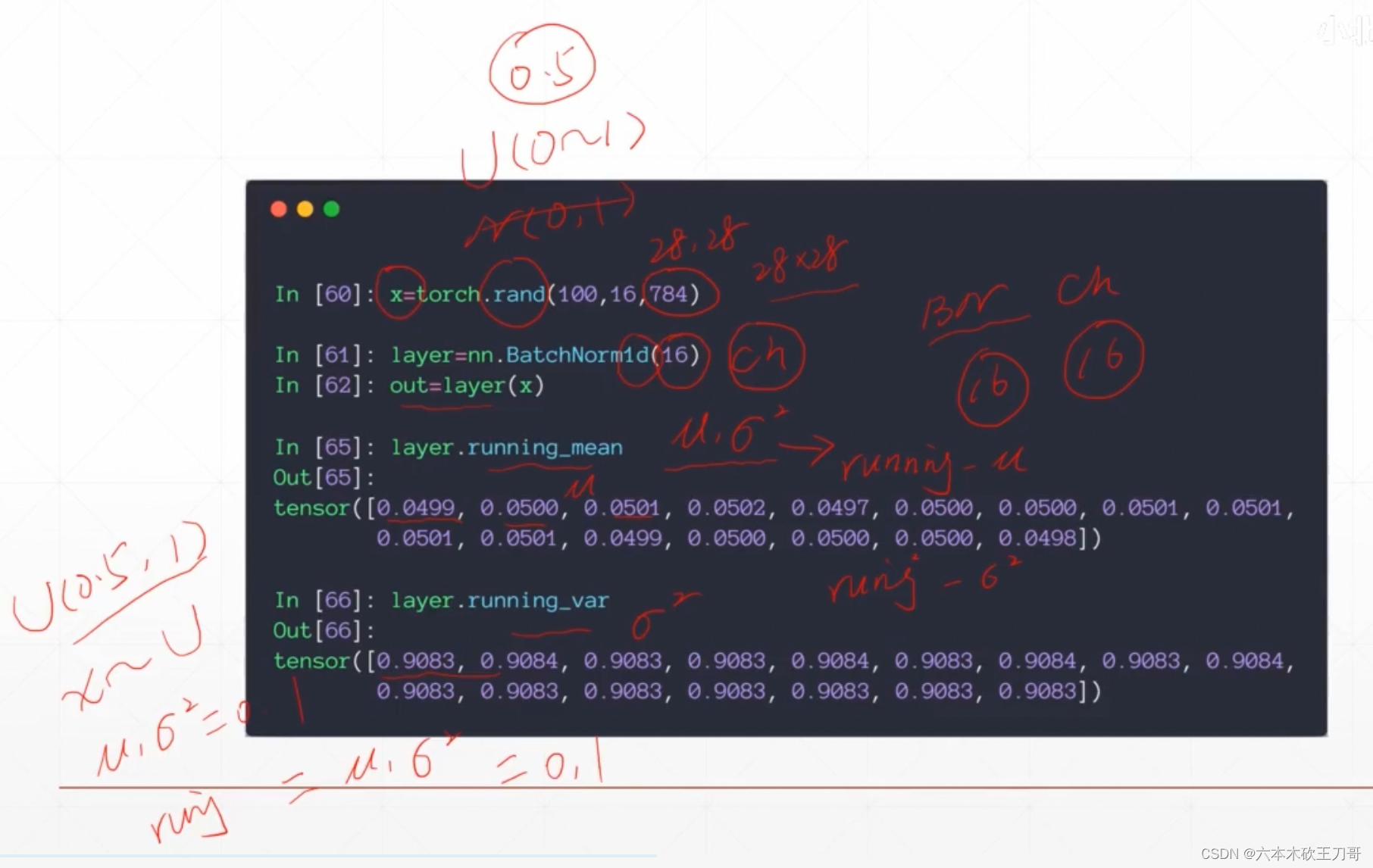
对BatchNorm举个例子，就是下面channel数量为3，共6张图片，那么可以分为3个6x784的格式，需要对其中每个channel都求均值和方差，然后得到两个1x3的向量，然后用这些均值和方差对原来的图片数据处理成一个新的分布，然后再对新的分布进行一次计算，这参数是需要学习的参数，而均值和方差是根据原数据求得的参数

用代码实现，rand是均值为0.5，方差为1的分布，所以求得BN之后得到的值符合这个分布

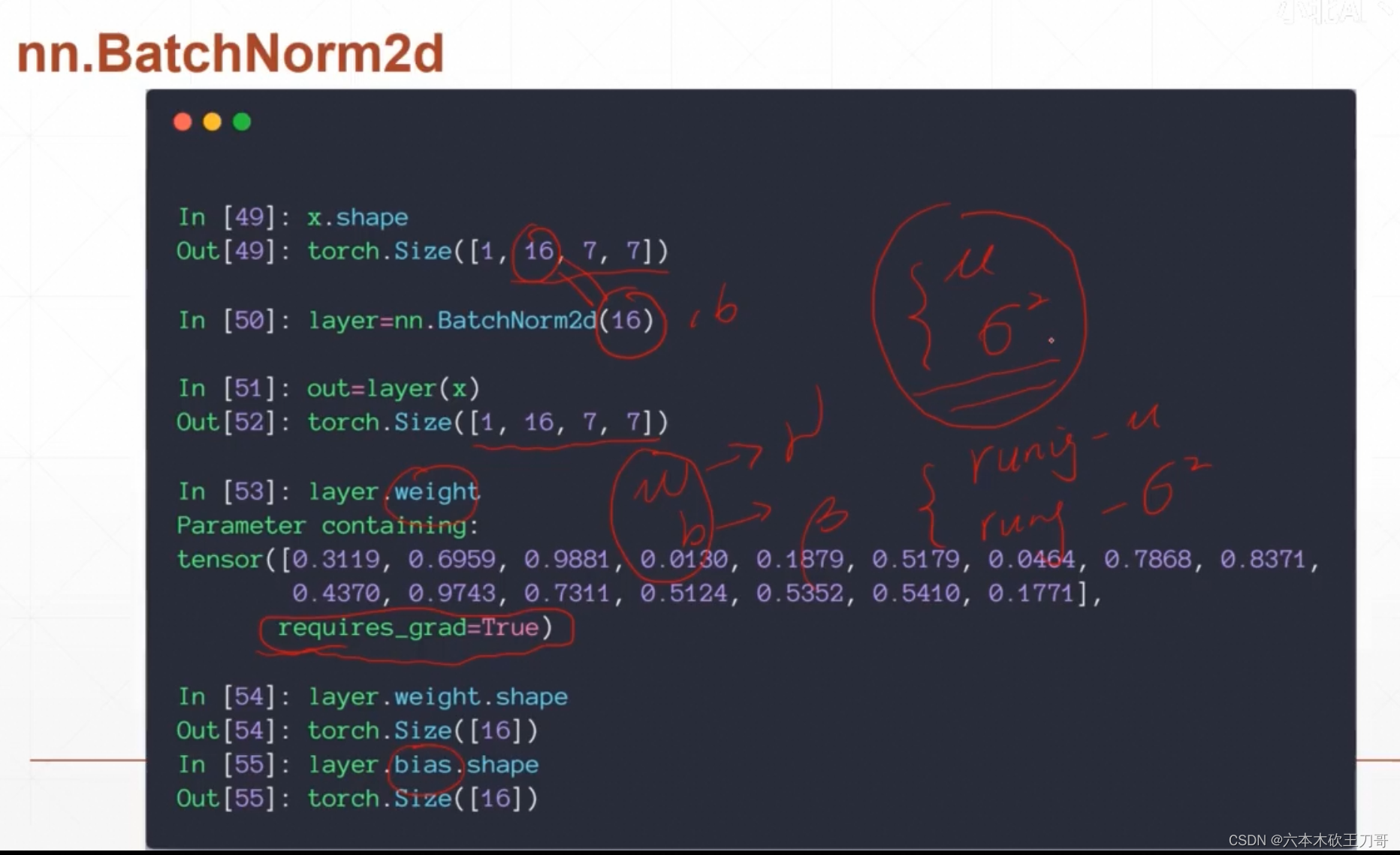
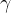
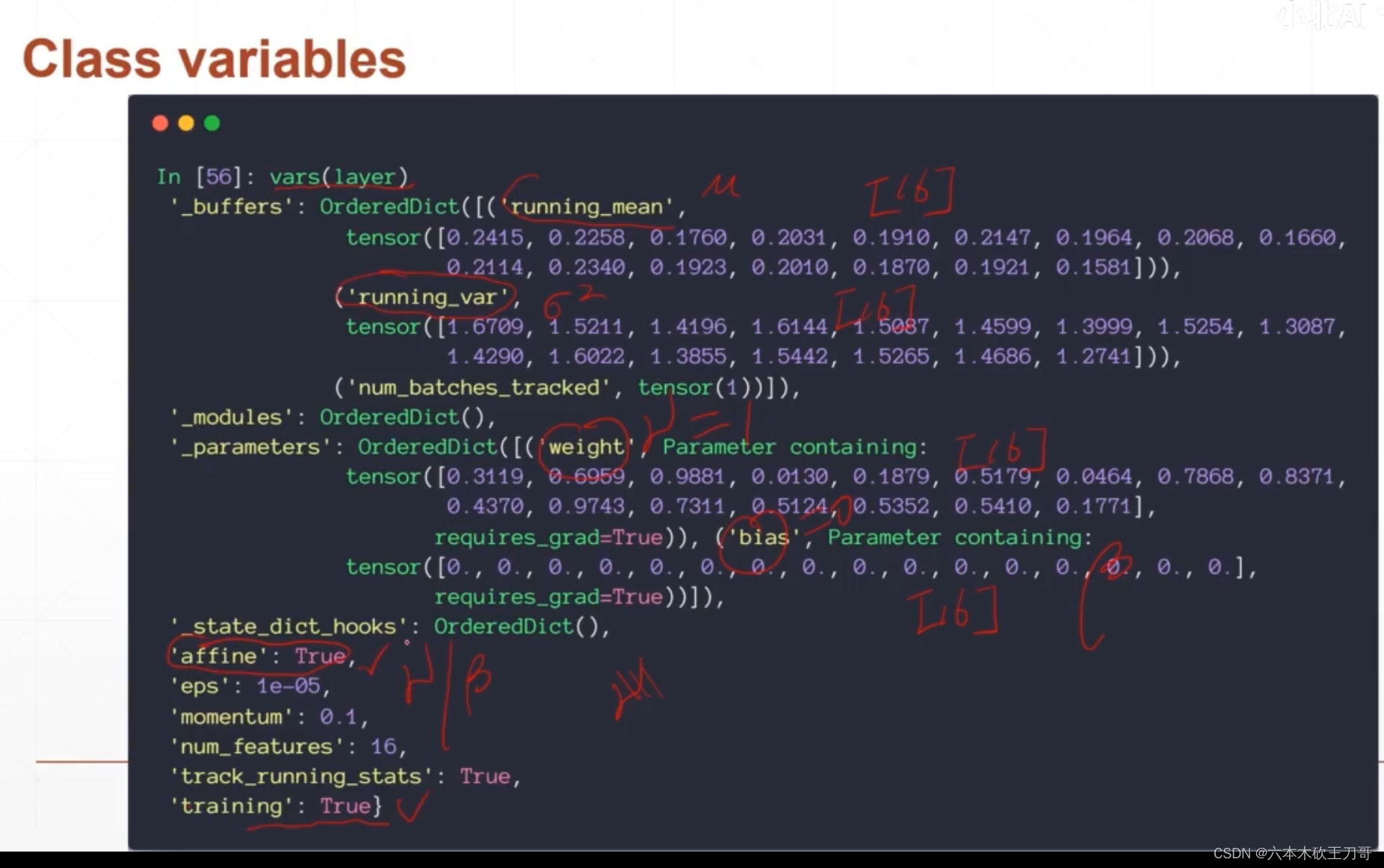
用二维来举例，这里weight是之前的，bias是

显示均值和方差 

 注意在训练和测试的时候是不一样的，这里均值和方差取的是全局的值，因为测试的时候没有很多图片输入，都是一个一个测试，然后也不需要的梯度。

15. 经典卷积神经网络

LeNET-5 手写数字识别

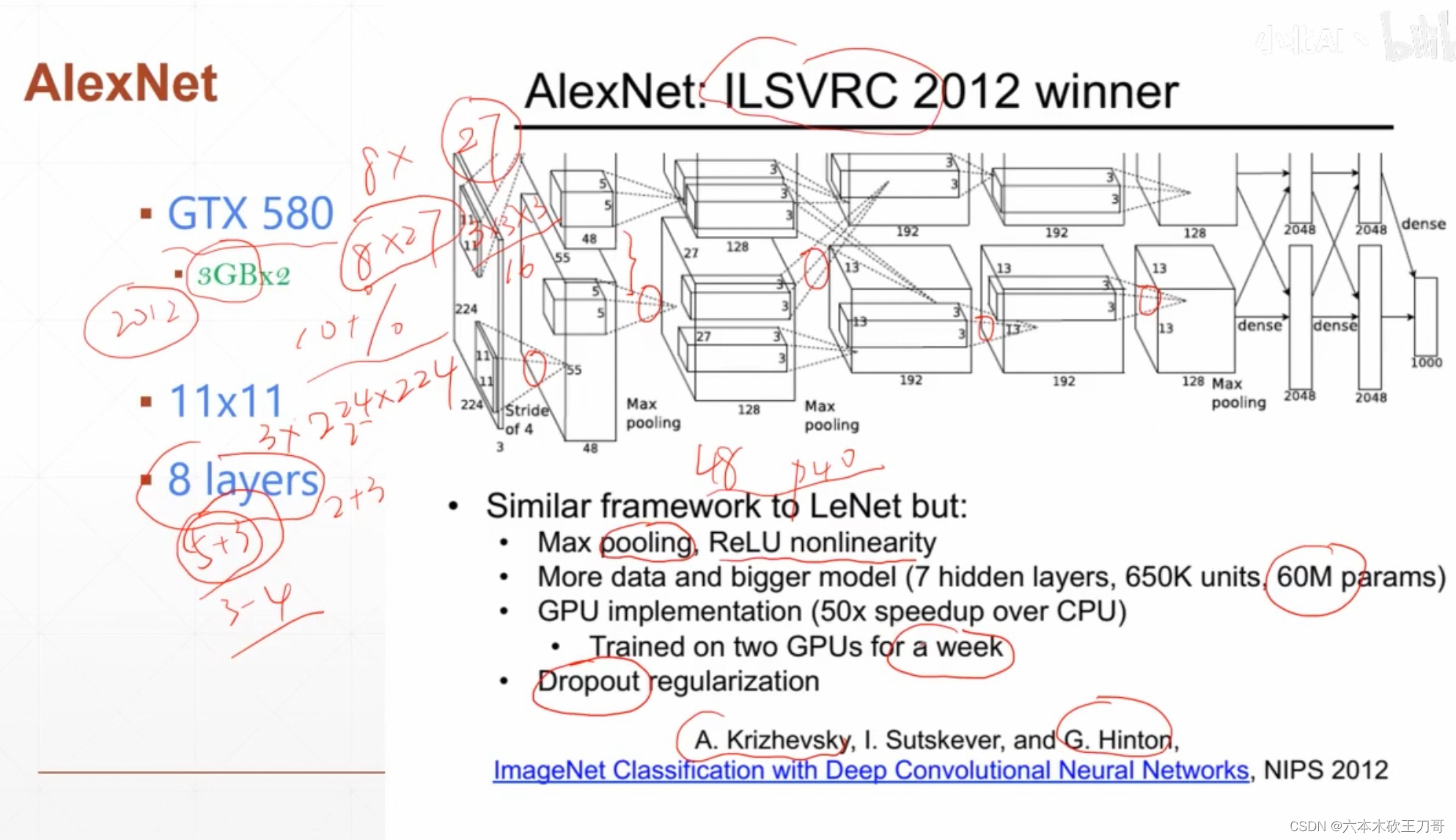
2012 AlexNet，使用了一些新的技术

2014 VGGNet

GoogLeNet -- 22层

堆叠更多层数反而不一定提高准确率

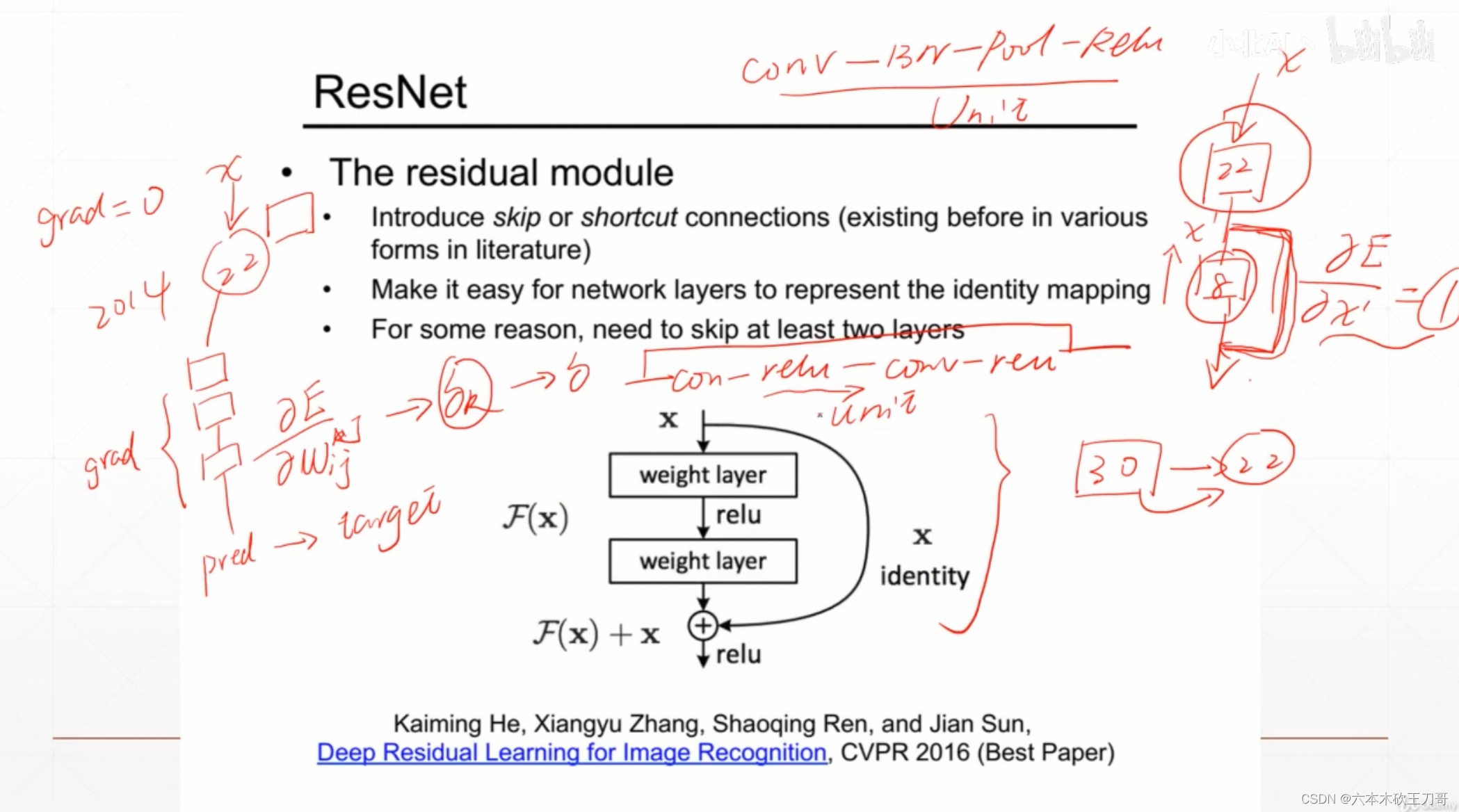
16. ResNet 深度残差网络 2016

17. nn.module类

module类

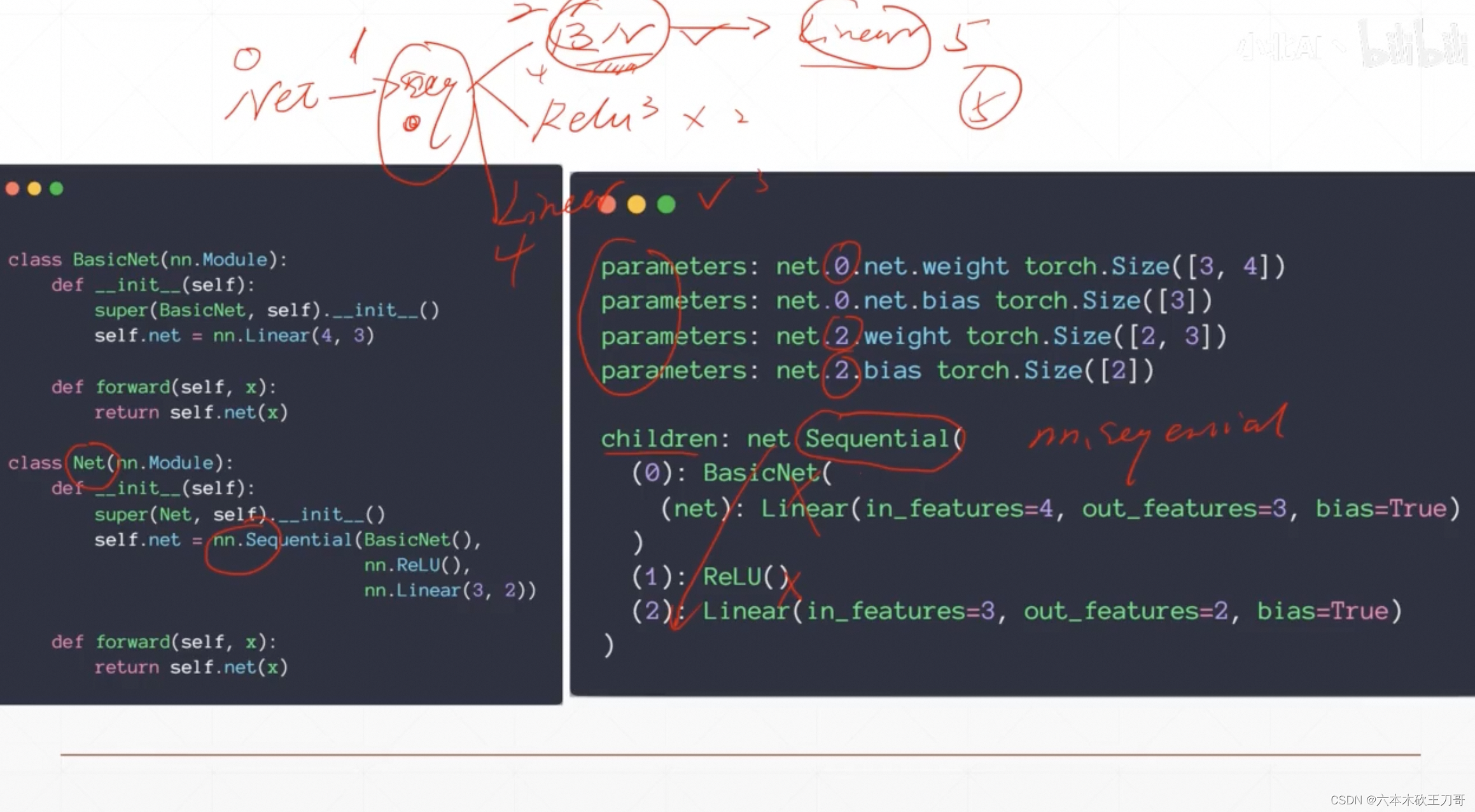
可以用Sequential作为容器

parameters会输出全部参数，例如下面是两个线性层，分别是输入4输出2，输入2输出2，然后每一层根据输出个数分别有Tensor元素个数为2的bias

可以看下面的测试输出 

>>> net=nn.Sequential(nn.Linear(4, 2), nn.Linear(2, 2))
>>> list(net.parameters())
[Parameter containing:
tensor([[ 0.0681, -0.4262,  0.0886,  0.2367],
        [ 0.4514,  0.1070,  0.2241, -0.1913]], requires_grad=True), Parameter containing:
tensor([ 0.4619, -0.2273], requires_grad=True), Parameter containing:
tensor([[0.3442, 0.5122],
        [0.3658, 0.0241]], requires_grad=True), Parameter containing:
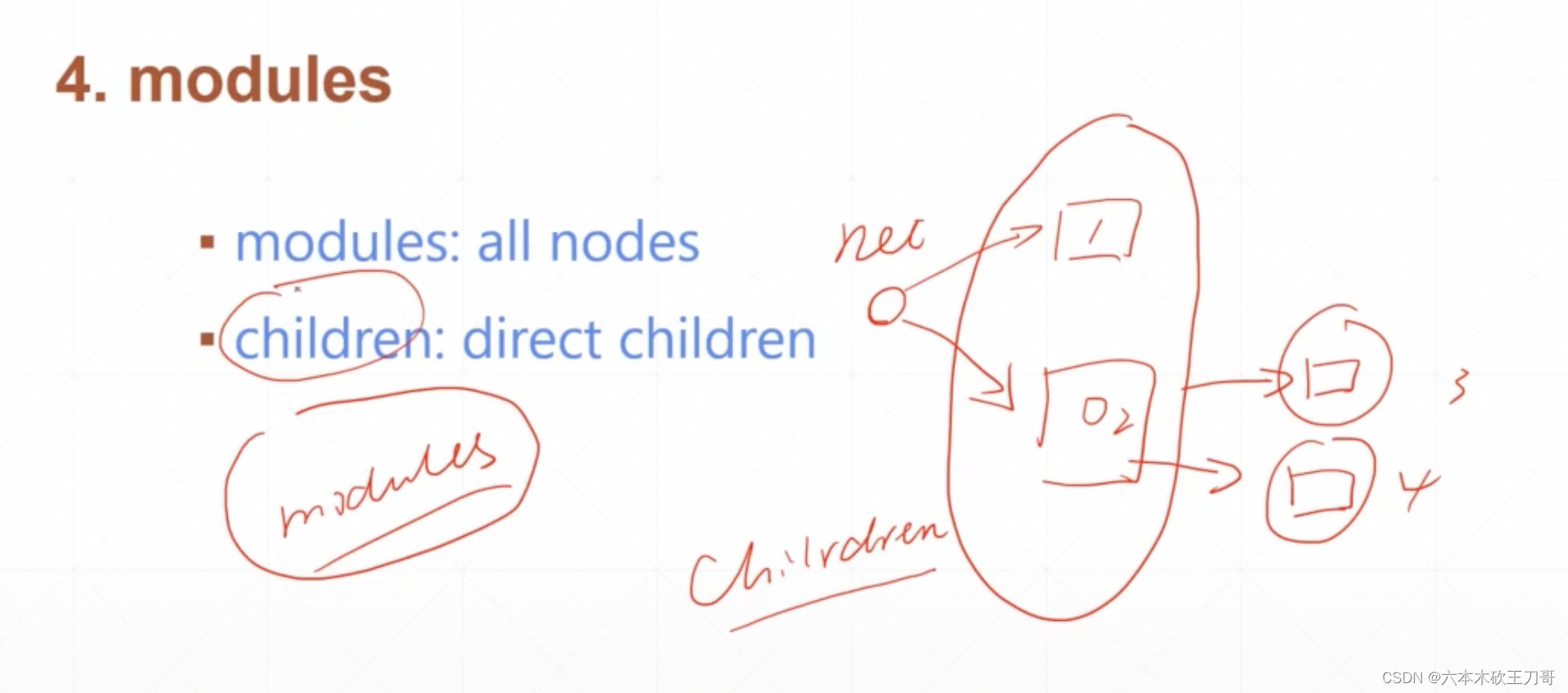
tensor([0.4413, 0.3187], requires_grad=True)]

 modules

打印出下面这个网络类的所有儿子，共有5个节点

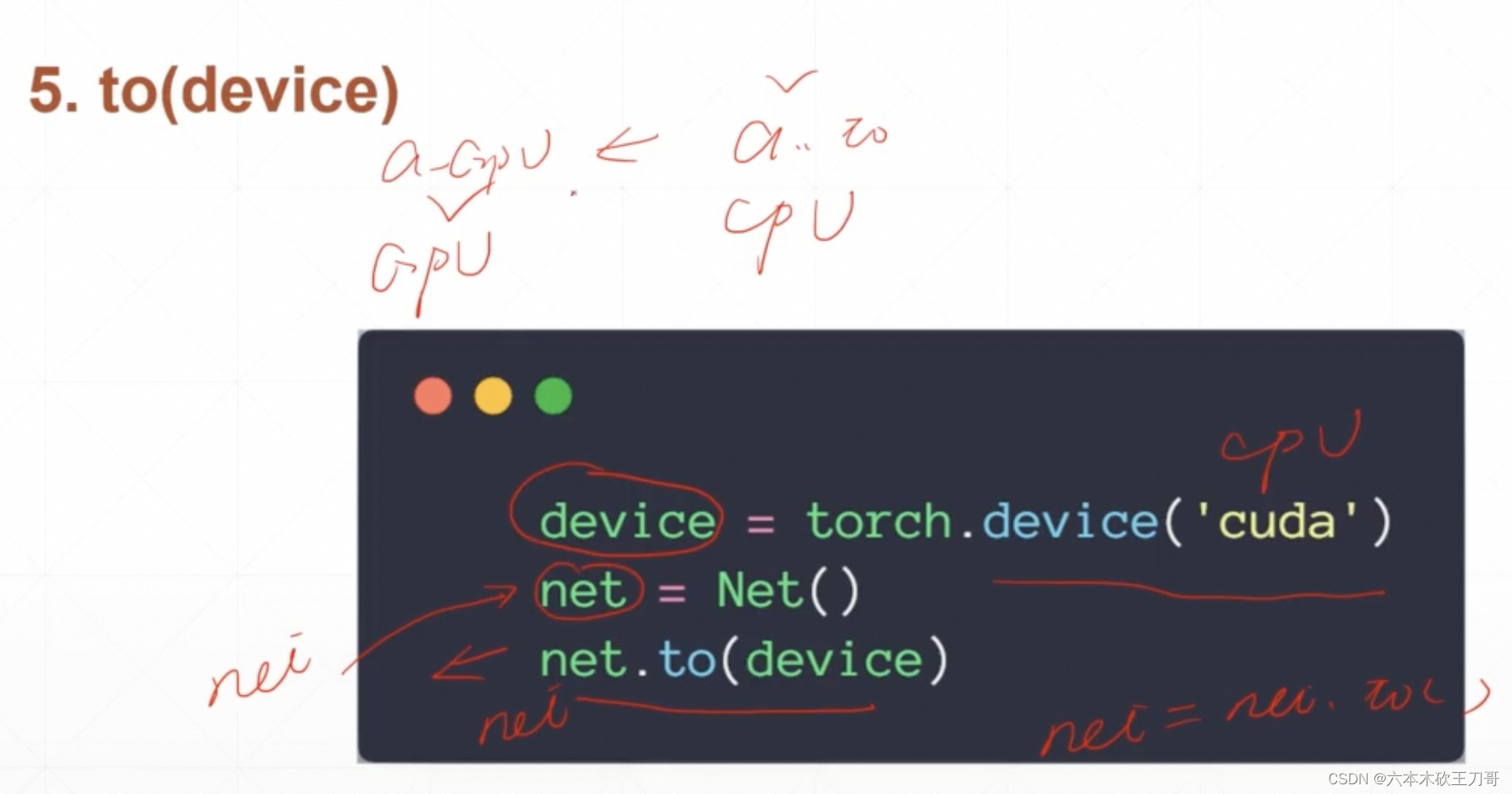
下一个功能是device，对于net来说，todevice的操作返回的都是同一个，但是对于一个tensor来说，todevice之后返回的对象就不一样了，gpu和cpu属性会发生改变

还需要保存和加载训练过程中的参数

训练和测试是不一样的，比如batchNorm，所以提供了训练和测试方法，自动完成这个操作

可以定义自己的类，比如展平一张图片的操作，需要写成类的形式，如果是直接调用view，nn Sequential无法接受函数的形式，并且写成函数前后连接两个Seq很不方便

 实现自己的类，把参数放在Parameter中，就不需要写require grad

18. 神经网络实战

主函数：

import  torch
from    torch.utils.data import DataLoader
from    torchvision import datasets
from    torchvision import transforms
from    torch import nn, optim

from    lenet5 import Lenet5
from    resnet import ResNet18

def main():
    batchsz = 128

    cifar_train = datasets.CIFAR10('cifar', True, transform=transforms.Compose([
        transforms.Resize((32, 32)),
        transforms.ToTensor(),
        transforms.Normalize(mean=[0.485, 0.456, 0.406],
                             std=[0.229, 0.224, 0.225])
    ]), download=True)
    cifar_train = DataLoader(cifar_train, batch_size=batchsz, shuffle=True)

    cifar_test = datasets.CIFAR10('cifar', False, transform=transforms.Compose([
        transforms.Resize((32, 32)),
        transforms.ToTensor(),
        transforms.Normalize(mean=[0.485, 0.456, 0.406],
                             std=[0.229, 0.224, 0.225])
    ]), download=True)
    cifar_test = DataLoader(cifar_test, batch_size=batchsz, shuffle=True)


    x, label = iter(cifar_train).next()
    print('x:', x.shape, 'label:', label.shape)

    device = torch.device('cuda')
    # model = Lenet5().to(device)
    model = ResNet18().to(device)

    criteon = nn.CrossEntropyLoss().to(device)
    optimizer = optim.Adam(model.parameters(), lr=1e-3)
    print(model)

    for epoch in range(1000):

        model.train()
        for batchidx, (x, label) in enumerate(cifar_train):
            # [b, 3, 32, 32]
            # [b]
            x, label = x.to(device), label.to(device)


            logits = model(x)
            # logits: [b, 10]
            # label:  [b]
            # loss: tensor scalar
            loss = criteon(logits, label)

            # backprop
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()


        print(epoch, 'loss:', loss.item())


        model.eval()
        with torch.no_grad():
            # test
            total_correct = 0
            total_num = 0
            for x, label in cifar_test:
                # [b, 3, 32, 32]
                # [b]
                x, label = x.to(device), label.to(device)

                # [b, 10]
                logits = model(x)
                # [b]
                pred = logits.argmax(dim=1)
                # [b] vs [b] => scalar tensor
                correct = torch.eq(pred, label).float().sum().item()
                total_correct += correct
                total_num += x.size(0)
                # print(correct)

            acc = total_correct / total_num
            print(epoch, 'test acc:', acc)



if __name__ == '__main__':
    main()

LeNet5实现

import  torch
from    torch import nn
from    torch.nn import functional as F




class Lenet5(nn.Module):
    """
    for cifar10 dataset.
    """
    def __init__(self):
        super(Lenet5, self).__init__()

        self.conv_unit = nn.Sequential(
            # x: [b, 3, 32, 32] => [b, 16, ]
            nn.Conv2d(3, 16, kernel_size=5, stride=1, padding=0),
            nn.MaxPool2d(kernel_size=2, stride=2, padding=0),
            #
            nn.Conv2d(16, 32, kernel_size=5, stride=1, padding=0),
            nn.MaxPool2d(kernel_size=2, stride=2, padding=0),
            #
        )
        # flatten
        # fc unit
        self.fc_unit = nn.Sequential(
            nn.Linear(32*5*5, 32),
            nn.ReLU(),
            # nn.Linear(120, 84),
            # nn.ReLU(),
            nn.Linear(32, 10)
        )


        # [b, 3, 32, 32]
        tmp = torch.randn(2, 3, 32, 32)
        out = self.conv_unit(tmp)
        # [b, 32, 5, 5]
        print('conv out:', out.shape)

        # # use Cross Entropy Loss
        # self.criteon = nn.CrossEntropyLoss()



    def forward(self, x):
        """

        :param x: [b, 3, 32, 32]
        :return:
        """
        batchsz = x.size(0)
        # [b, 3, 32, 32] => [b, 32, 5, 5]
        x = self.conv_unit(x)
        # [b, 16, 5, 5] => [b, 32*5*5]
        x = x.view(batchsz, 32*5*5)
        # [b, 32*5*5] => [b, 10]
        logits = self.fc_unit(x)

        # # [b, 10]
        # pred = F.softmax(logits, dim=1)
        # loss = self.criteon(logits, y)

        return logits

def main():

    net = Lenet5()

    tmp = torch.randn(2, 3, 32, 32)
    out = net(tmp)
    print('lenet out:', out.shape)




if __name__ == '__main__':
    main()

 ResNet实现

import  torch
from    torch import  nn
from    torch.nn import functional as F



class ResBlk(nn.Module):
    """
    resnet block
    """

    def __init__(self, ch_in, ch_out, stride=1):
        """

        :param ch_in:
        :param ch_out:
        """
        super(ResBlk, self).__init__()

        # we add stride support for resbok, which is distinct from tutorials.
        self.conv1 = nn.Conv2d(ch_in, ch_out, kernel_size=3, stride=stride, padding=1)
        self.bn1 = nn.BatchNorm2d(ch_out)
        self.conv2 = nn.Conv2d(ch_out, ch_out, kernel_size=3, stride=1, padding=1)
        self.bn2 = nn.BatchNorm2d(ch_out)

        self.extra = nn.Sequential()
        if ch_out != ch_in:
            # [b, ch_in, h, w] => [b, ch_out, h, w]
            self.extra = nn.Sequential(
                nn.Conv2d(ch_in, ch_out, kernel_size=1, stride=stride),
                nn.BatchNorm2d(ch_out)
            )


    def forward(self, x):
        """

        :param x: [b, ch, h, w]
        :return:
        """
        out = F.relu(self.bn1(self.conv1(x)))
        out = self.bn2(self.conv2(out))
        # short cut.
        # extra module: [b, ch_in, h, w] => [b, ch_out, h, w]
        # element-wise add:
        out = self.extra(x) + out
        out = F.relu(out)
        
        return out




class ResNet18(nn.Module):

    def __init__(self):
        super(ResNet18, self).__init__()

        self.conv1 = nn.Sequential(
            nn.Conv2d(3, 64, kernel_size=3, stride=3, padding=0),
            nn.BatchNorm2d(64)
        )
        # followed 4 blocks
        # [b, 64, h, w] => [b, 128, h ,w]
        self.blk1 = ResBlk(64, 128, stride=2)
        # [b, 128, h, w] => [b, 256, h, w]
        self.blk2 = ResBlk(128, 256, stride=2)
        # # [b, 256, h, w] => [b, 512, h, w]
        self.blk3 = ResBlk(256, 512, stride=2)
        # # [b, 512, h, w] => [b, 1024, h, w]
        self.blk4 = ResBlk(512, 512, stride=2)

        self.outlayer = nn.Linear(512*1*1, 10)

    def forward(self, x):
        """

        :param x:
        :return:
        """
        x = F.relu(self.conv1(x))

        # [b, 64, h, w] => [b, 1024, h, w]
        x = self.blk1(x)
        x = self.blk2(x)
        x = self.blk3(x)
        x = self.blk4(x)


        # print('after conv:', x.shape) #[b, 512, 2, 2]
        # [b, 512, h, w] => [b, 512, 1, 1]
        x = F.adaptive_avg_pool2d(x, [1, 1])
        # print('after pool:', x.shape)
        x = x.view(x.size(0), -1)
        x = self.outlayer(x)


        return x



def main():

    blk = ResBlk(64, 128, stride=4)
    tmp = torch.randn(2, 64, 32, 32)
    out = blk(tmp)
    print('block:', out.shape)

    x = torch.randn(2, 3, 32, 32)
    model = ResNet18()
    out = model(x)
    print('resnet:', out.shape)




if __name__ == '__main__':
    main()

19. 序列，RNN

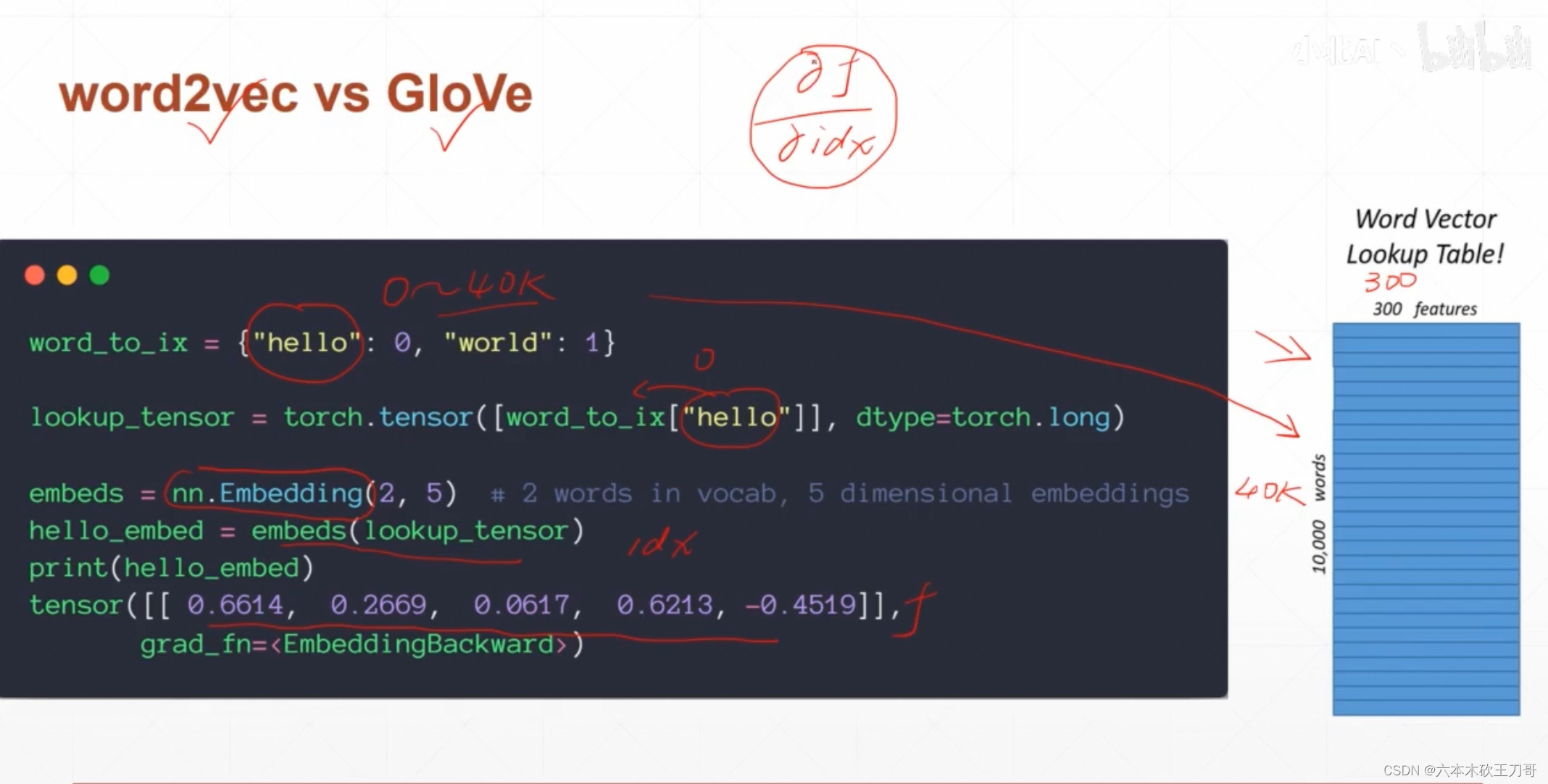
使用Pytorch来生成一个随机的词向量查找表，当然也可以使用已经用w2v生成好的表格但是无法优化

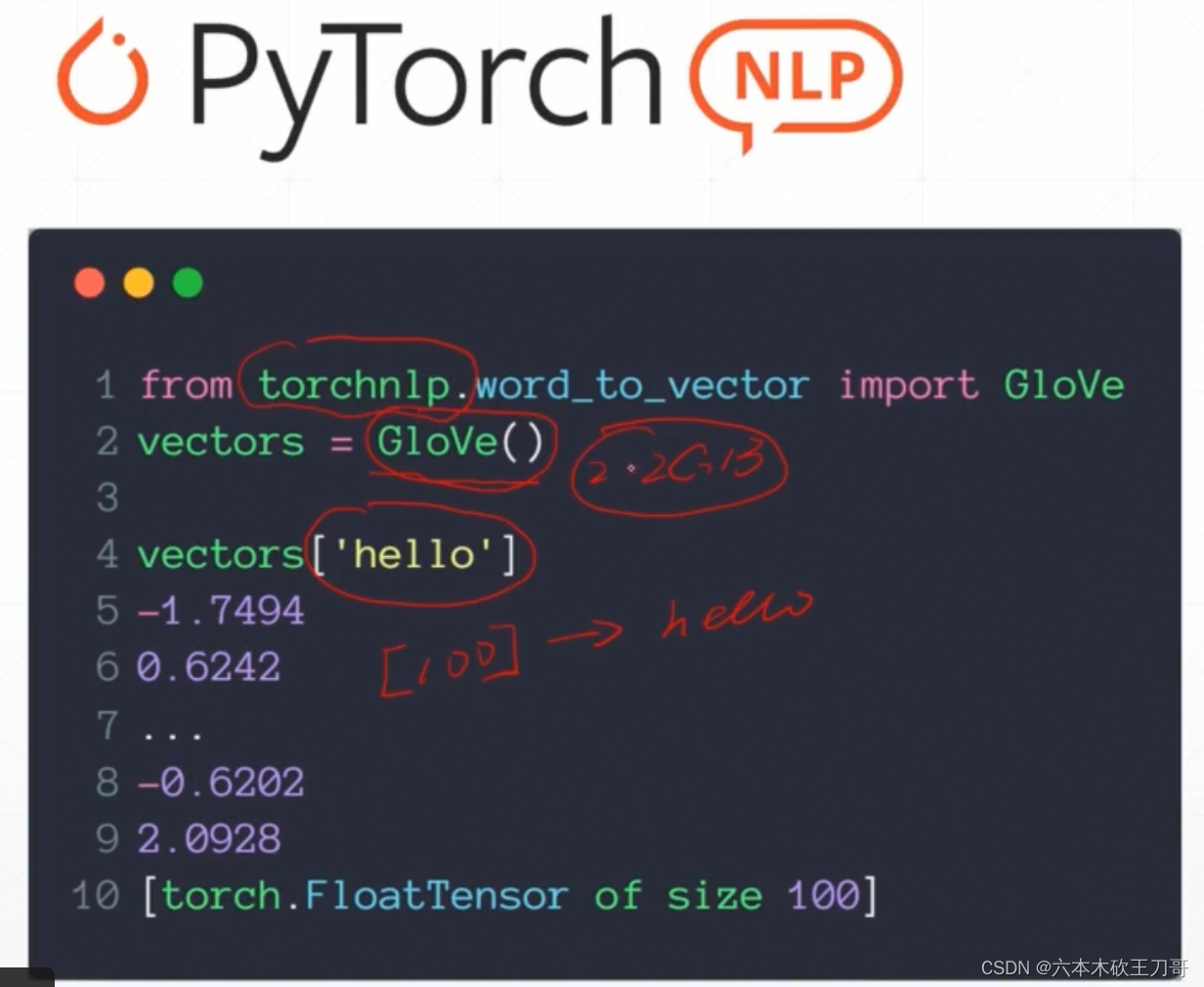
使用Pytorch已经有的Glove库下载查找表，可以查找对应单词的向量表示

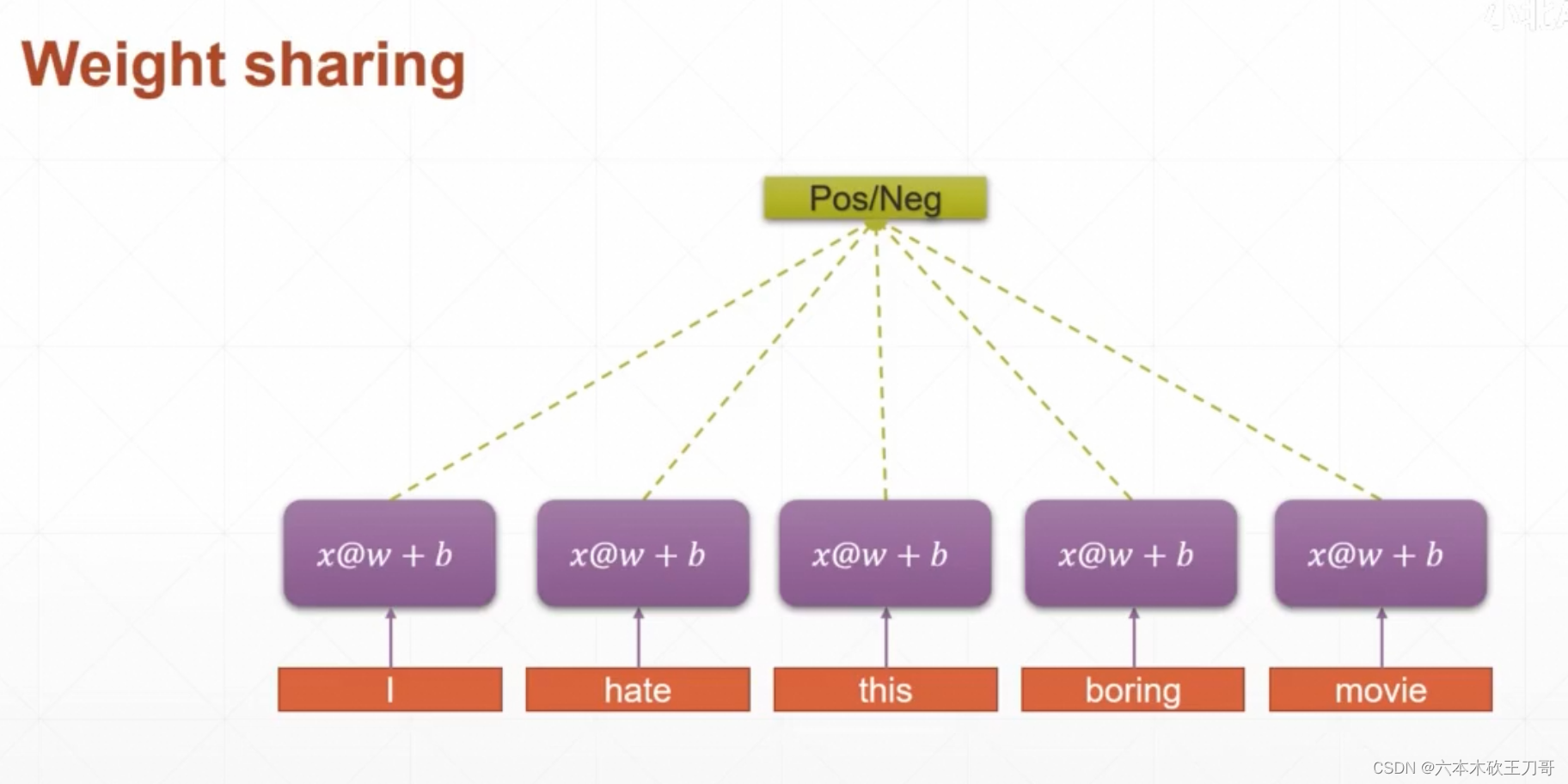
如果使用常规的手段，根据之前的方法得到每个单词的词向量（例如是5个100维数据），然后输入到对应的线性层之后，得到一个假设是2维的输出，最后进行判断

但是这种方法是有问题的，首先就是如果句子过长的话，会带来参数量过多的问题，然后第二点就是无法处理语境，得不到句子内部的相关性信息，一种解决方法就是参数共享，每个单词都经过一样的线性单元

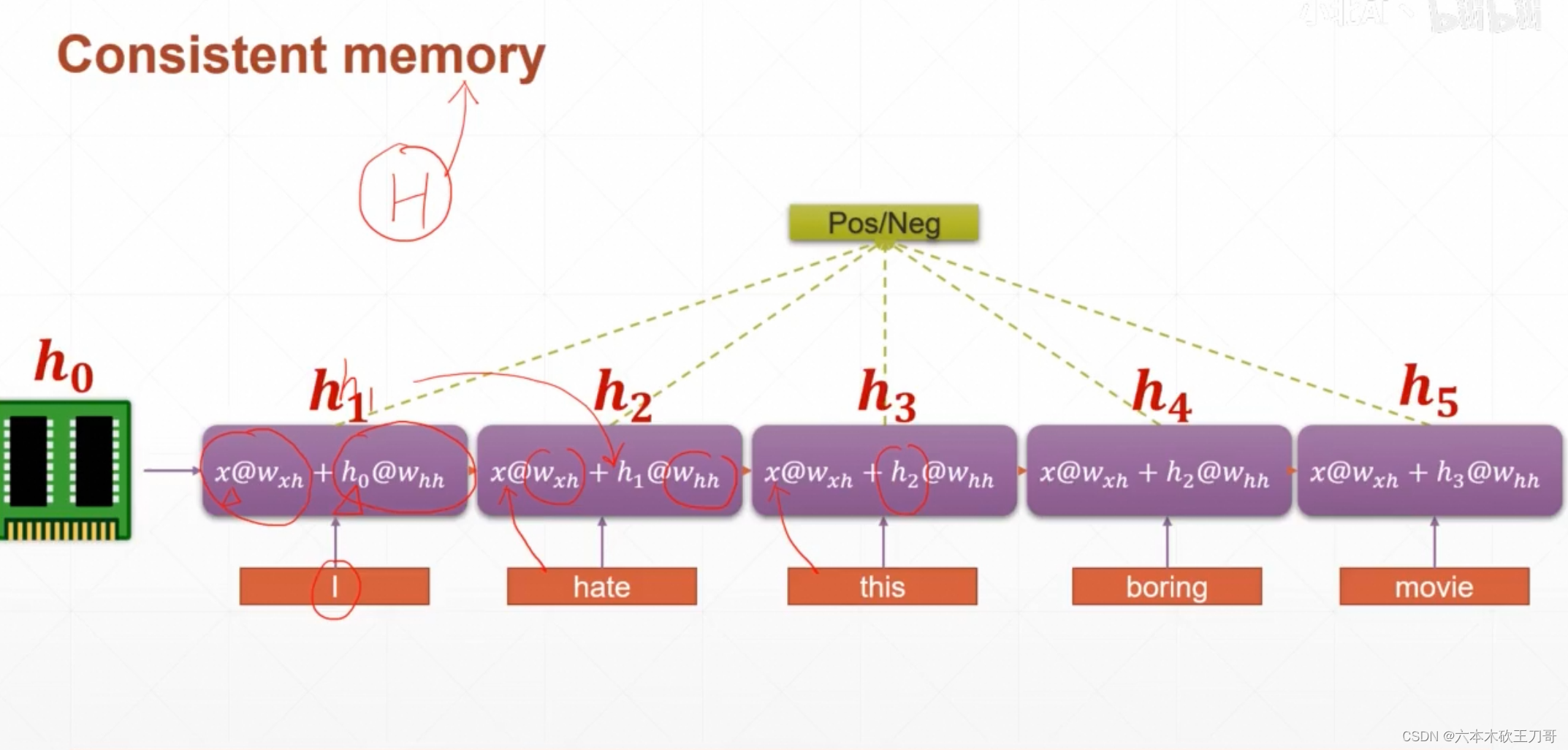
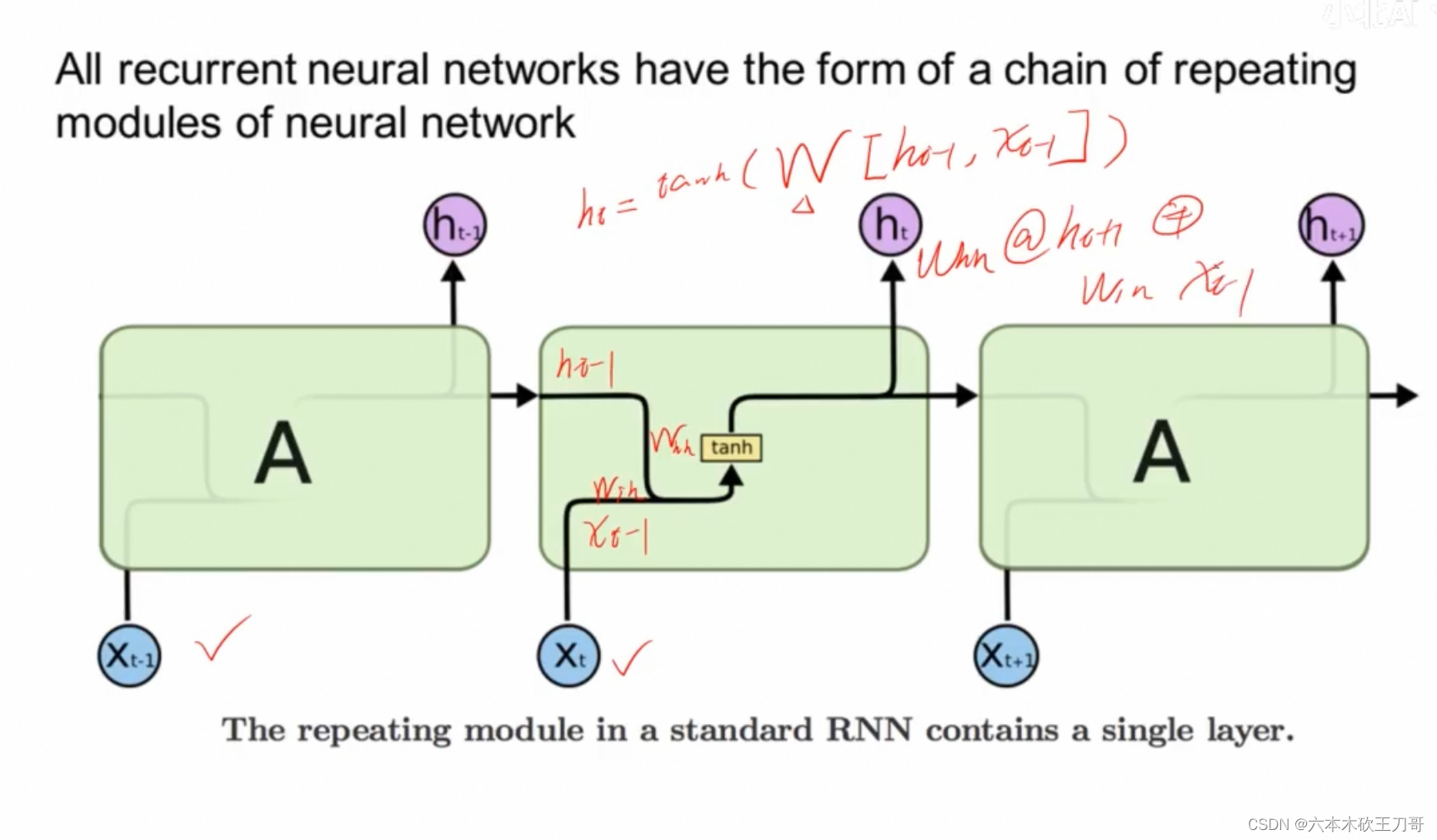
为了得到持续性的信息，需要加入一个记忆的单元h，首先初始化一个h0，然后第一次输入一个单词x的时候，处理完这个x*w，再加上h0乘上对应权重，之后把整个单元变成h1，当下一个输入进来的时候，乘上对应权重再加上这个h1的部分，以此类推。

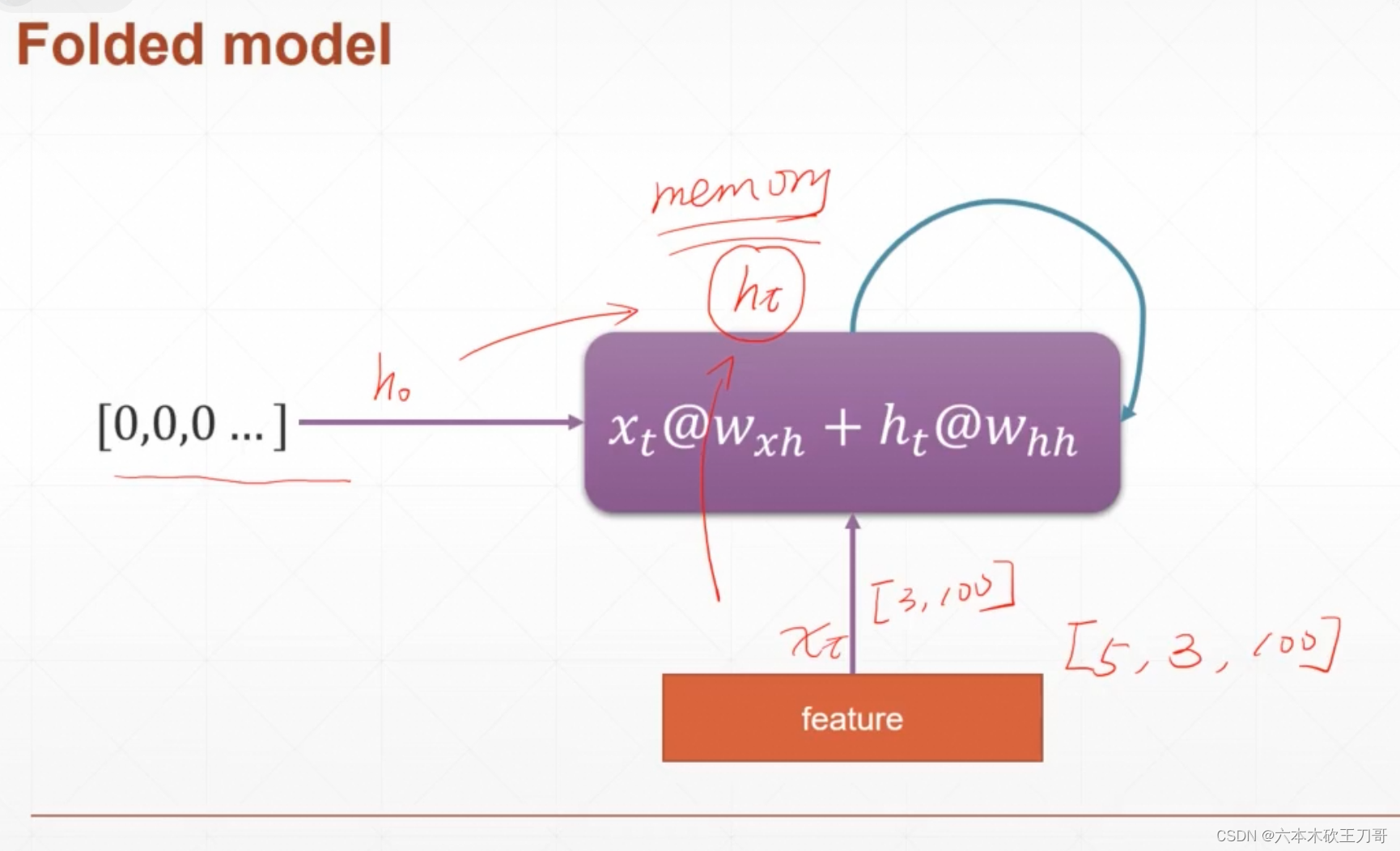
例如输入句子长度是5，batch是3，每个单词的维度是100，所以输入就是[5, 3, 100]，那么对应每次的输入单词x就是[3, 100]，输入到对应单元之后就一直循环滚动，之前的输出作为h，之后的输入作为新x。

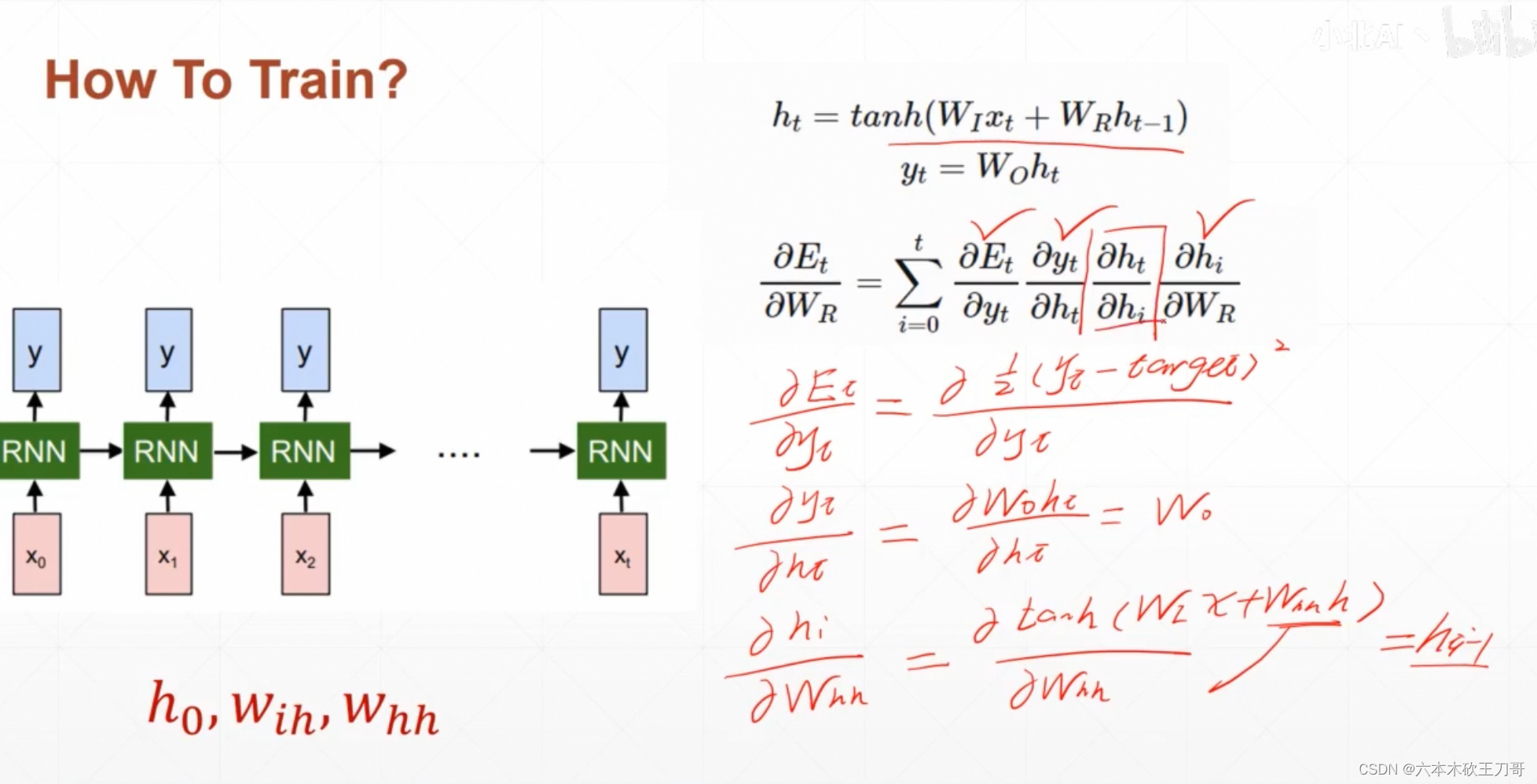
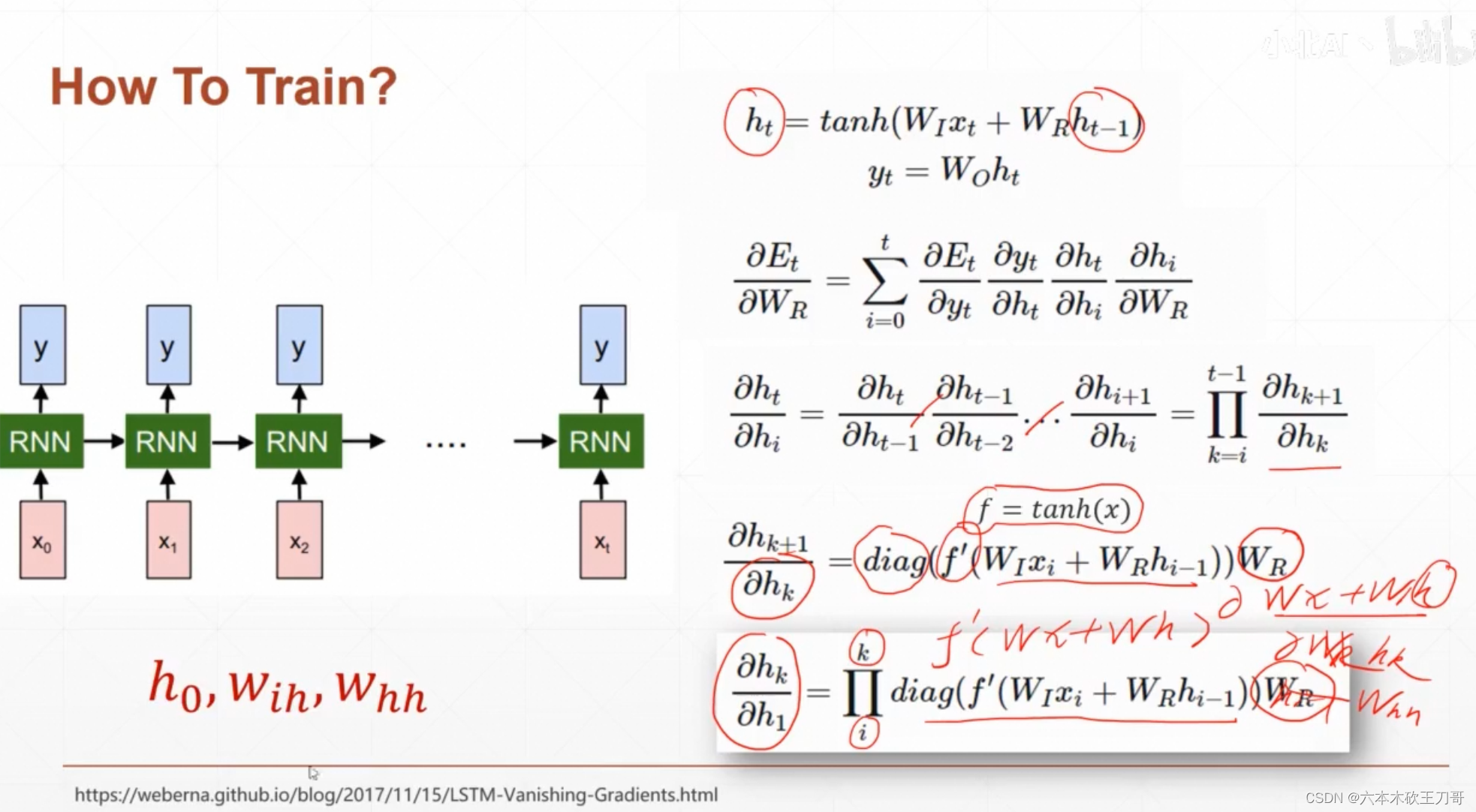
推导一下从ht-1到ht和输出yt的公式，这里yt只不过是一个线性变换

推导RNN的梯度计算，第一步列出ht的前向传播公式，然后参数矩阵Wr（就是之前的Whh）对误差Et求偏导，其实对时刻t的误差Et来说，0到t的Wt参数都对Et有影响，所以需要一个累加。

对于这个公式中的四个导数，其中三个很好求，hi对Wr只要把ht公式中的t换成i就可以。

重点是第三个导数如何求，t时刻的ht对i时刻的hi求导数，可以把整个时间都展开，可以得到一个链式求导公式，然后其中每一项都是前一个时刻对后一个时刻求导，单独对这个hk+1对hk求导，直接就是上面公式求导就可以了（ht对ht-1求导），最后把所有项累乘即可。

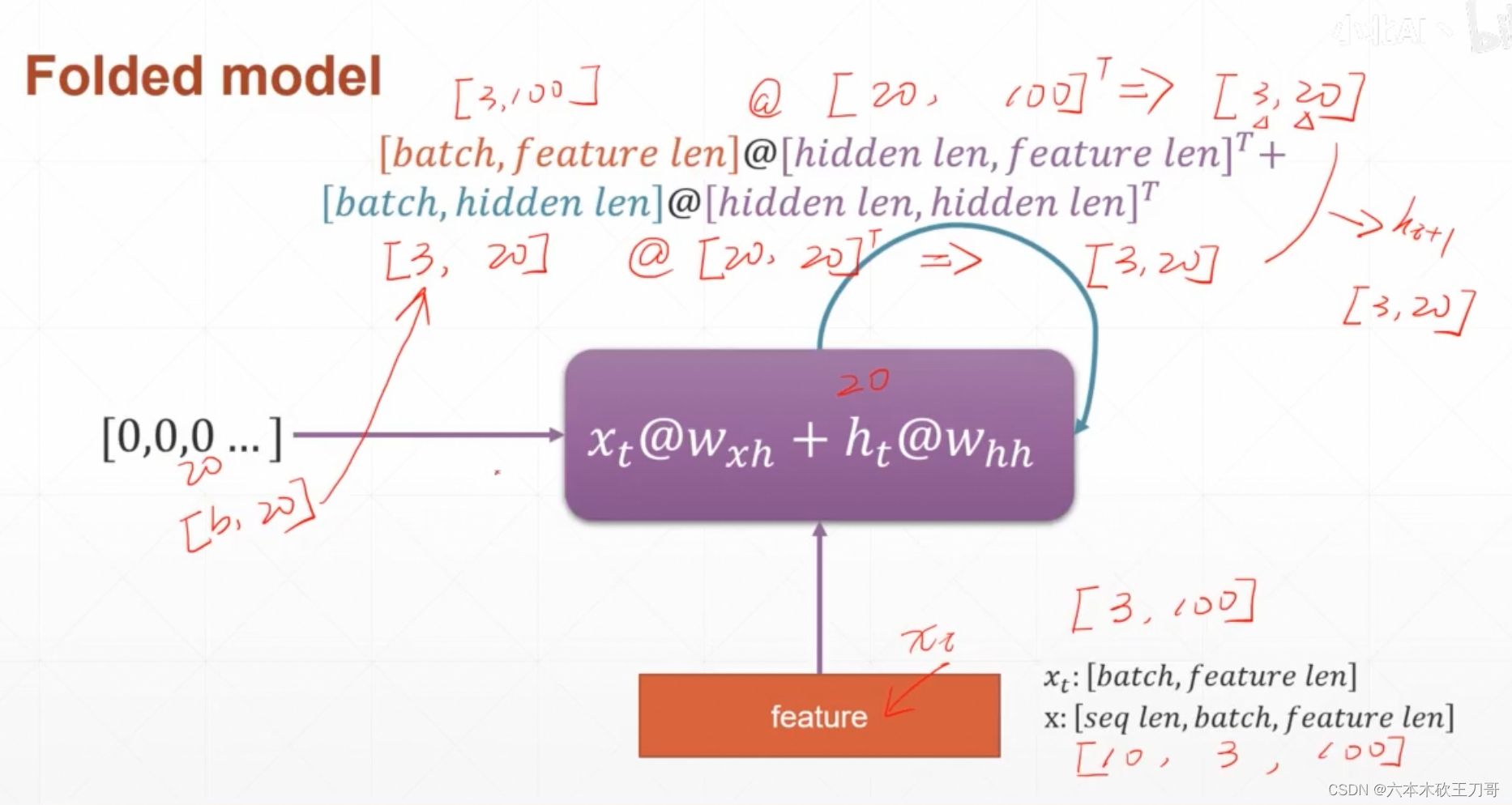
 RNN在pytorch中的表示，首先需要明确输入，假设句子的长度是10，然后batch是3，每个单词的长度是100，所以这个向量表示就是[10, 3, 100]，RNN每层输入就是一个单词，也就是[3, 100]，然后乘上一个参数Wxh，假设hidden len是20，就是[3, 100] * [100, 20] 得到 [3, 20]，这个就是每个ht的维度，这个维度的ht-1乘上Whh累加上即可，最终得到的维度就是[3, 20]。

代码中设置RNN的单词维度是100，memory维度也就是hidden len为10，这样得到Wih和Whh的维度分别是[10, 10]以及[10, 100]，bias就是对应的偏置。

 初始化函数

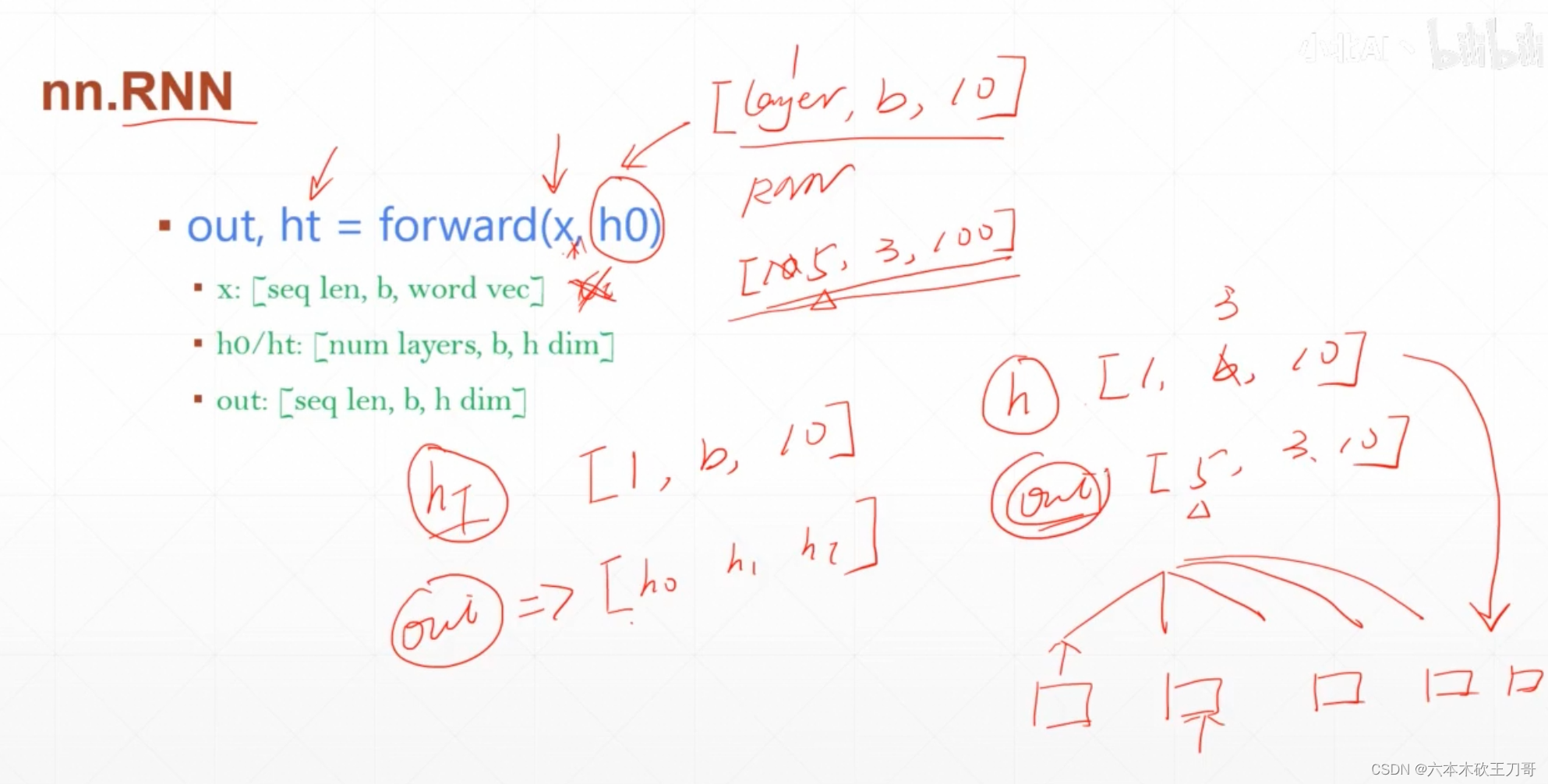
forward函数，其中x就是全部输入，这里不需要管每次的输入[3, 100]，直接把全部输入[5, 3, 100]送入就可以，h0就是初始的输入，维度是[batch, hidden lenth]，在下面代码中的维度是[num layers, batch, hidden lenth]，layers对应单层来说layers就是1，多层就是别的数，（h是RNN每次计算的输出或者中间需要的上一时刻的h），如果不写函数里的h0的话，就是自动设置为全0，注意别把h的维度和W的维度搞混。

ht是最后t时刻的memory，例如维度是[1, 3, 10]，batch是3，memory或者说是hidden len是10。假设句子的长度是5，那么RNN就需要喂入5次数据并计算，out是全部时刻的memory一起输出，最后的结果就是把h0，h1，h2到h4五次计算结果都放在一起，所以维度就是[5, 3, 10]。

 单层RNN示例，输入单词维度是100维，hidden size是20，layer是1层，输入x单词数量是10，batch数量是3，维度是100必须和RNN的参数对上。

接下来就是输入rnn进行计算，x是输入的句子，第二个参数就是全0的h0，注意h和out的维度。

两层RNN举例，h会变但是out不会，因为out是每个时间的最后一个输出，不管有几层，都是结合最后一层的输出，所以只和输入句子的长度有关，比如长度是10，那么就计算10次，所以out就是10维。

验证layer是2的RNN，其中l0是从100维转换为10维，l1还是10维。 

对于一个4层的RNN来说，针对100维单词，memory是20的情况下，输入x是三句长度为10的句子，然后验证h和out的维度，分别是[4, 3, 20]和[10, 3, 20]

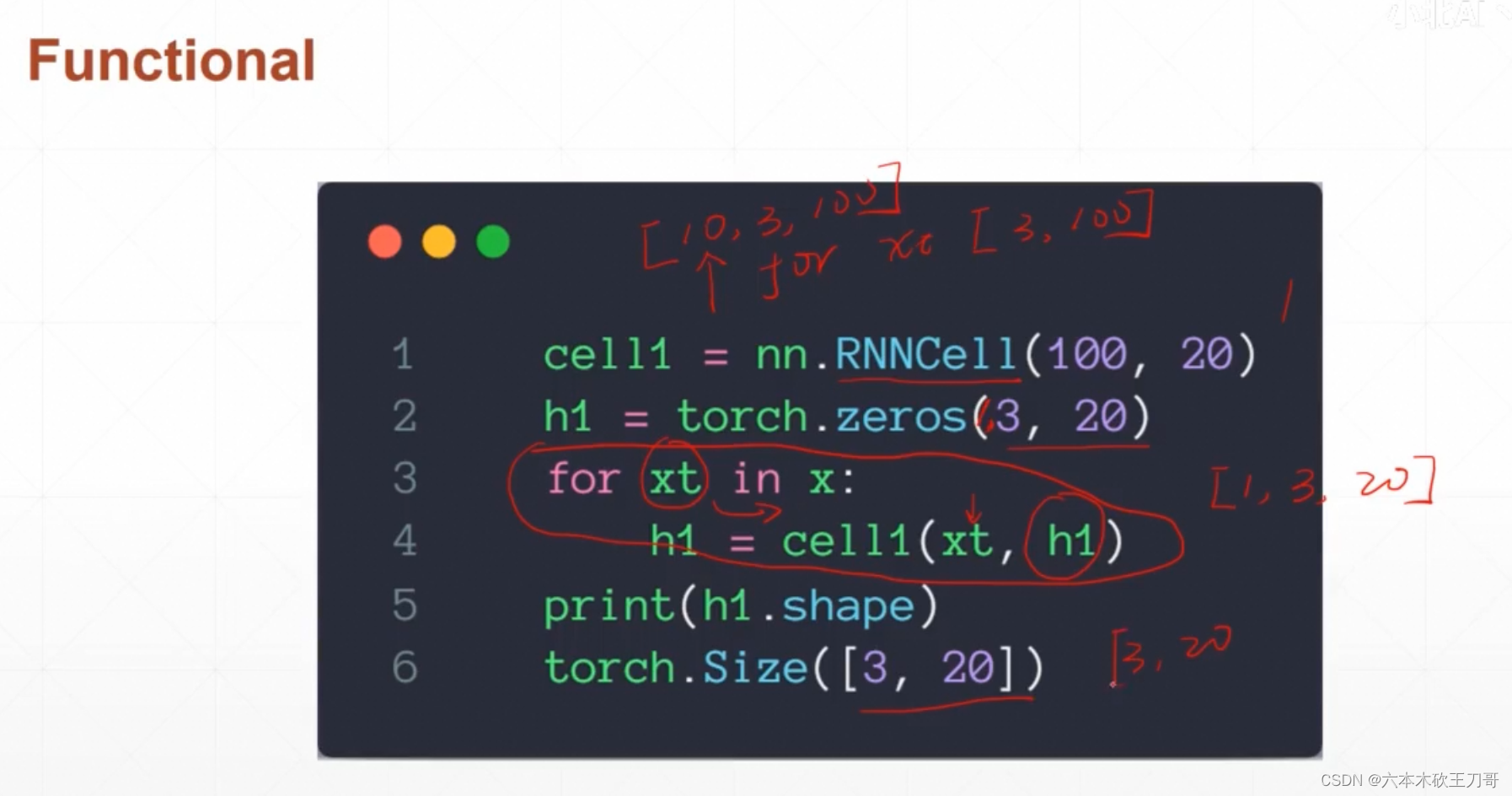
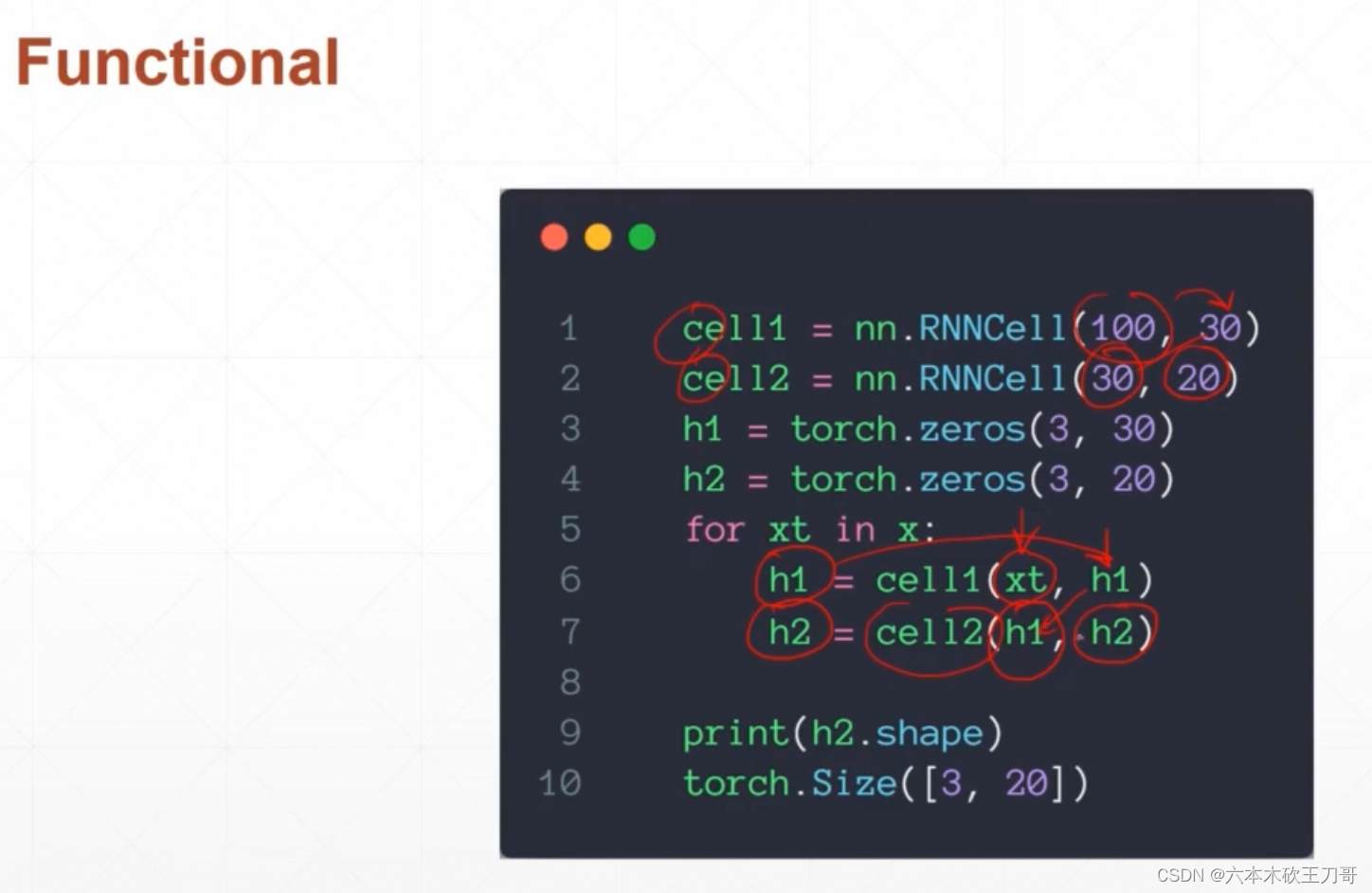
可以手动喂多次，使用RNNCell每次只完成一次计算，和之前的RNN参数是一样的。

但是forward参数是不一样的， 这里x每次只输入一个，例如[3, 100]，h还是[4, 3, 10]这种格式

使用循环来构建单层RNN计算过程，从[10, 3, 100]中每次抽取[3, 100]这种格式，最后输出的h1维度是[3, 20]

构建两层的RNN计算，只不过需要多加一层h的计算

20. 时间序列预测RNN

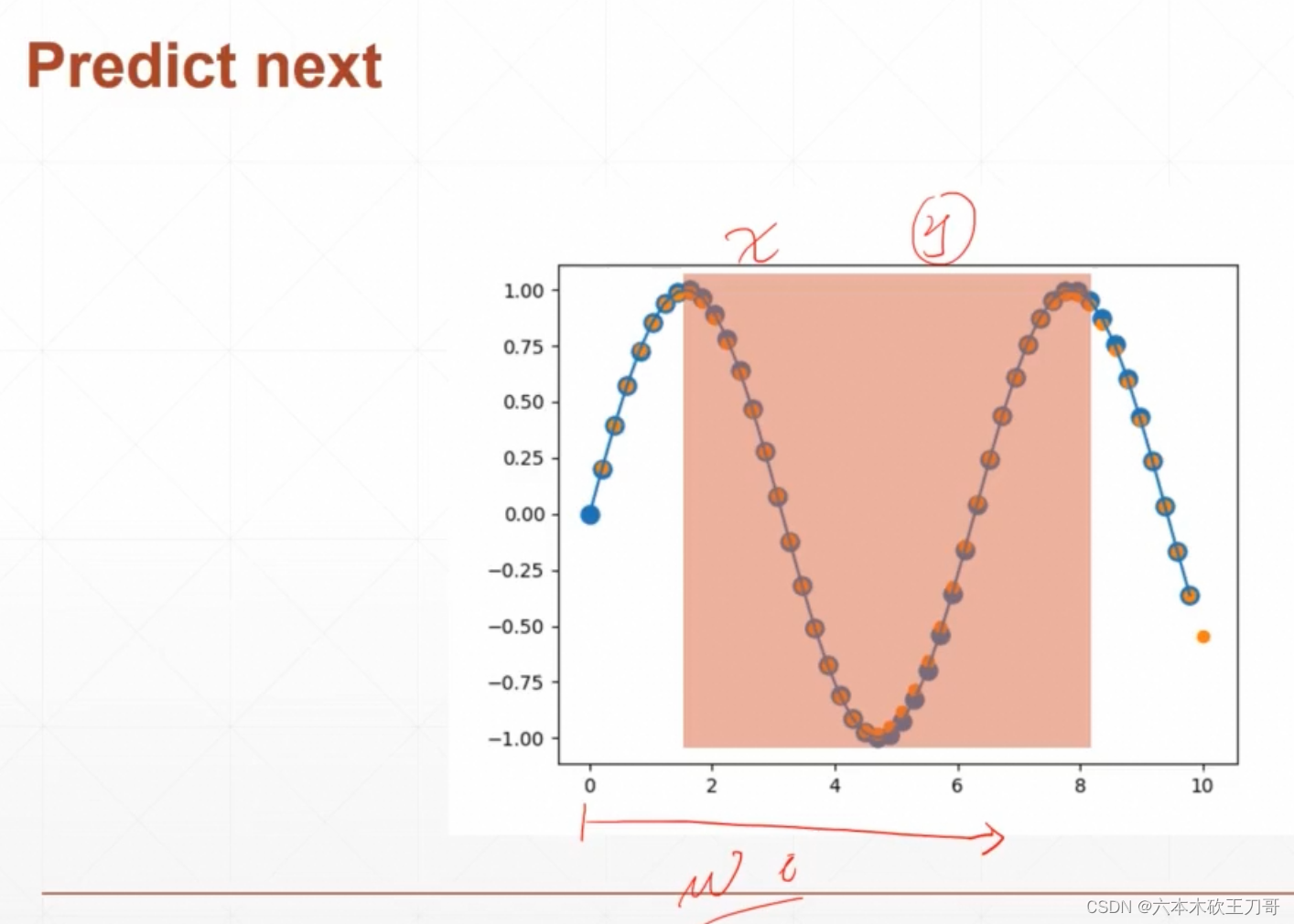
这里送入一条都是数字的曲线，每个数字不需要embedding，因为它只有一个值。换一种表达方式，把batch值放到第一个位置，这时候表示就是[1, 50, 1]，它代表送一条曲线，每条曲线的点数是50，不需要embedding的话只有一个数字而不是向量。在随机生成点的时候是先在0～3中随机一个数字，然后这里没听明白（为了防止网络记住？）。之后的模式就是输入例如0～48位置的数字，然后往后预测一个数字，就是1～49的数字。

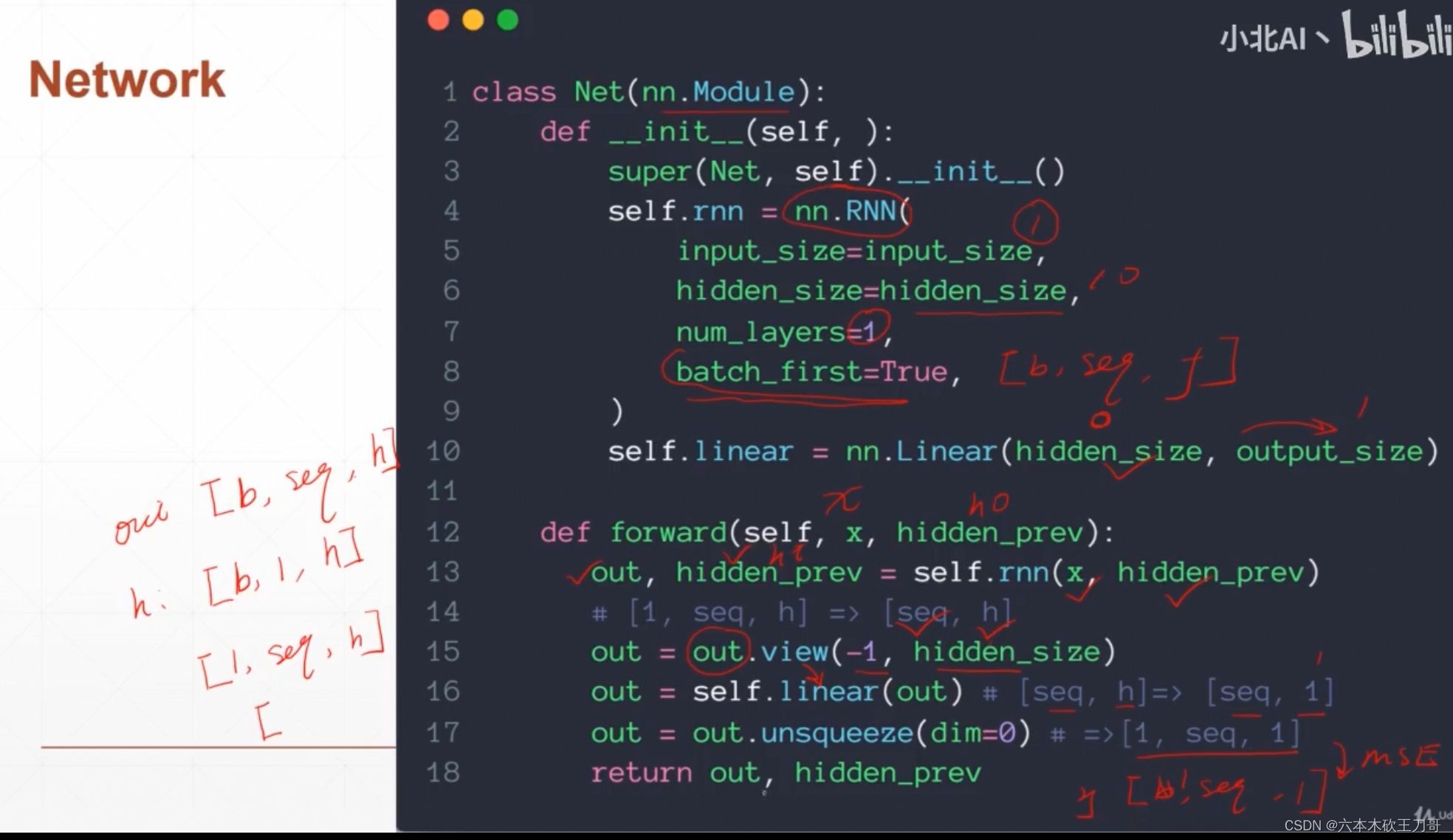
网络定义，input和output size是1。在前向计算的时候需要送入rnn层，rnn的参数是输入x和h0，输出是out和ht，如果batch是1的话，那么out的输出就是[1, seq, hidden len]，然后需要把out展平再输入linear层，最后插入第一个维度1，因为这里需要和正确输出y做比较计算loss。

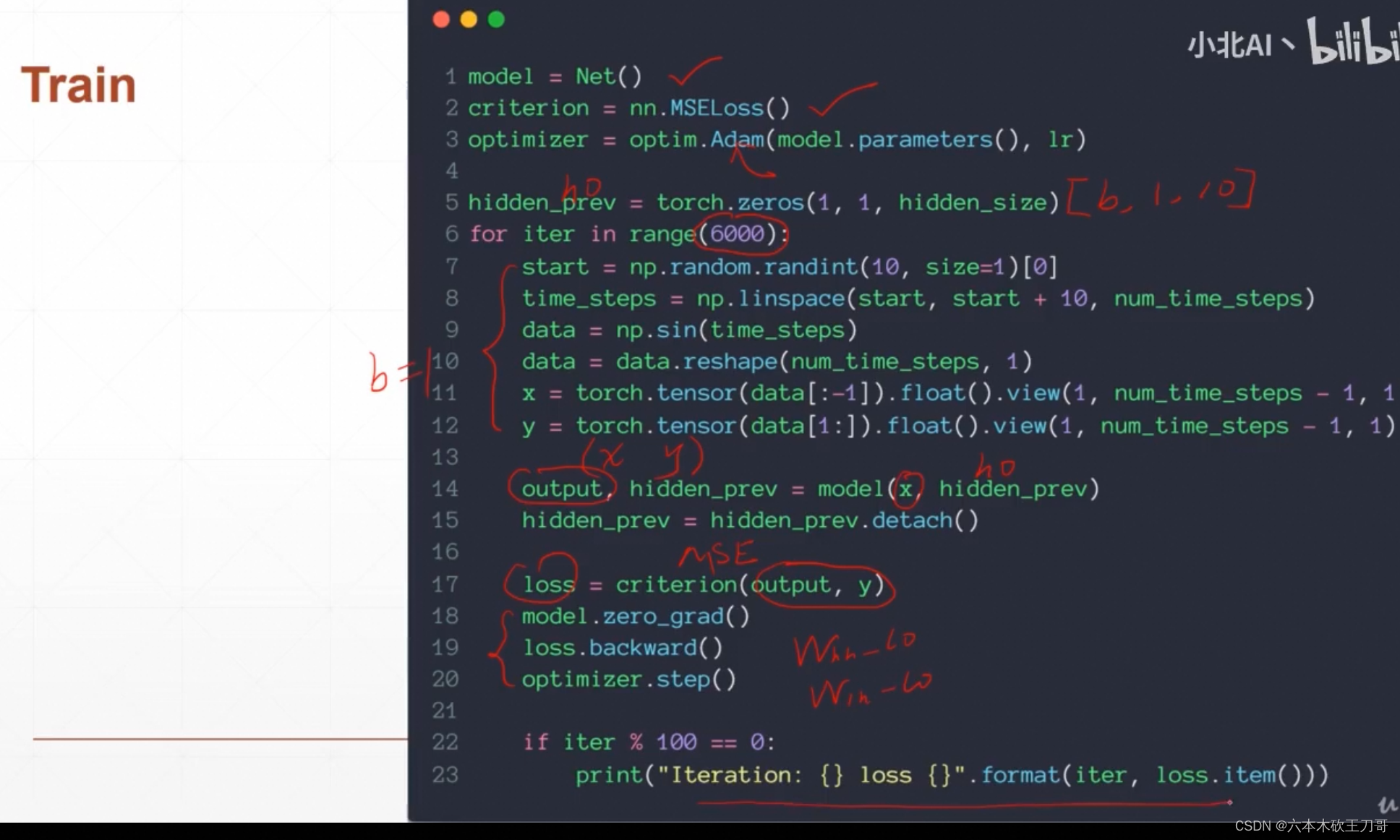
训练过程就是随机生成x和y，来计算loss 

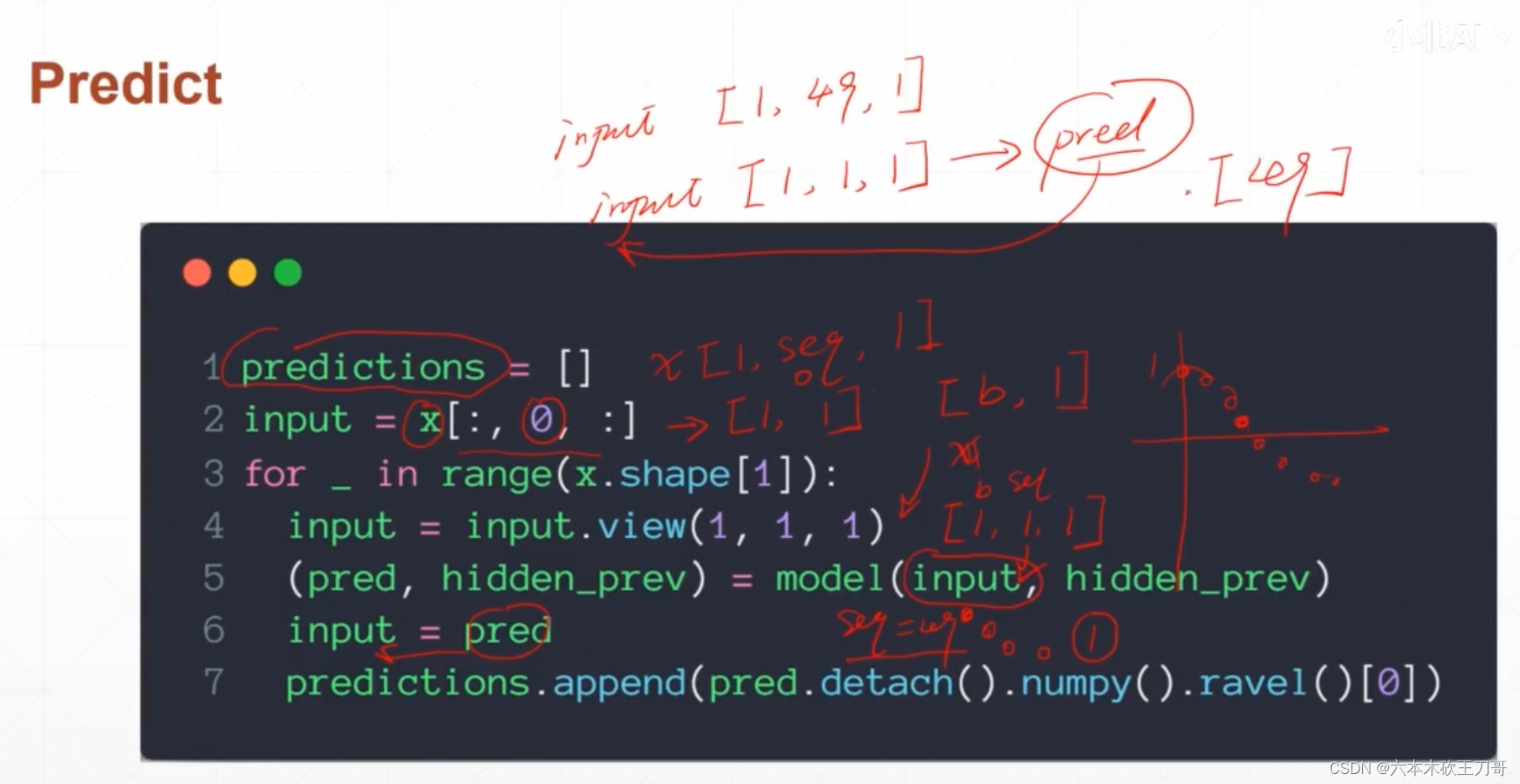
预测过程就是随机生成一个[1, 1, 1]的点，然后通过初试点去更新下一个点，把更新的点作为下一次的input，这样记录下来把图画出来就可以

完整代码如下：

import  numpy as np
import  torch
import  torch.nn as nn
import  torch.optim as optim
from    matplotlib import pyplot as plt


num_time_steps = 50
input_size = 1
hidden_size = 16
output_size = 1
lr=0.01



class Net(nn.Module):

    def __init__(self, ):
        super(Net, self).__init__()

        self.rnn = nn.RNN(
            input_size=input_size,
            hidden_size=hidden_size,
            num_layers=1,
            batch_first=True,
        )
        for p in self.rnn.parameters():
          nn.init.normal_(p, mean=0.0, std=0.001)

        self.linear = nn.Linear(hidden_size, output_size)

    def forward(self, x, hidden_prev):

       out, hidden_prev = self.rnn(x, hidden_prev)
       # [b, seq, h]
       out = out.view(-1, hidden_size)
       out = self.linear(out)
       out = out.unsqueeze(dim=0)
       return out, hidden_prev




model = Net()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr)

hidden_prev = torch.zeros(1, 1, hidden_size)

for iter in range(6000):
    start = np.random.randint(3, size=1)[0]
    time_steps = np.linspace(start, start + 10, num_time_steps)
    data = np.sin(time_steps)
    data = data.reshape(num_time_steps, 1)
    x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
    y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)

    output, hidden_prev = model(x, hidden_prev)
    hidden_prev = hidden_prev.detach()

    loss = criterion(output, y)
    model.zero_grad()
    loss.backward()
    # for p in model.parameters():
    #     print(p.grad.norm())
    # torch.nn.utils.clip_grad_norm_(p, 10)
    optimizer.step()

    if iter % 100 == 0:
        print("Iteration: {} loss {}".format(iter, loss.item()))

start = np.random.randint(3, size=1)[0]
time_steps = np.linspace(start, start + 10, num_time_steps)
data = np.sin(time_steps)
data = data.reshape(num_time_steps, 1)
x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)

predictions = []
input = x[:, 0, :]
for _ in range(x.shape[1]):
  input = input.view(1, 1, 1)
  (pred, hidden_prev) = model(input, hidden_prev)
  input = pred
  predictions.append(pred.detach().numpy().ravel()[0])

x = x.data.numpy().ravel()
y = y.data.numpy()
plt.scatter(time_steps[:-1], x.ravel(), s=90)
plt.plot(time_steps[:-1], x.ravel())

plt.scatter(time_steps[1:], predictions)
plt.show()

21. 梯度弥散和梯度爆炸

在RNN的梯度更新过程中，会有一个Whh的k次方的计算过程，k代表了这个序列的长度，这个如果过大或者过小都会累积到最后导致出现梯度弥散和爆炸的问题

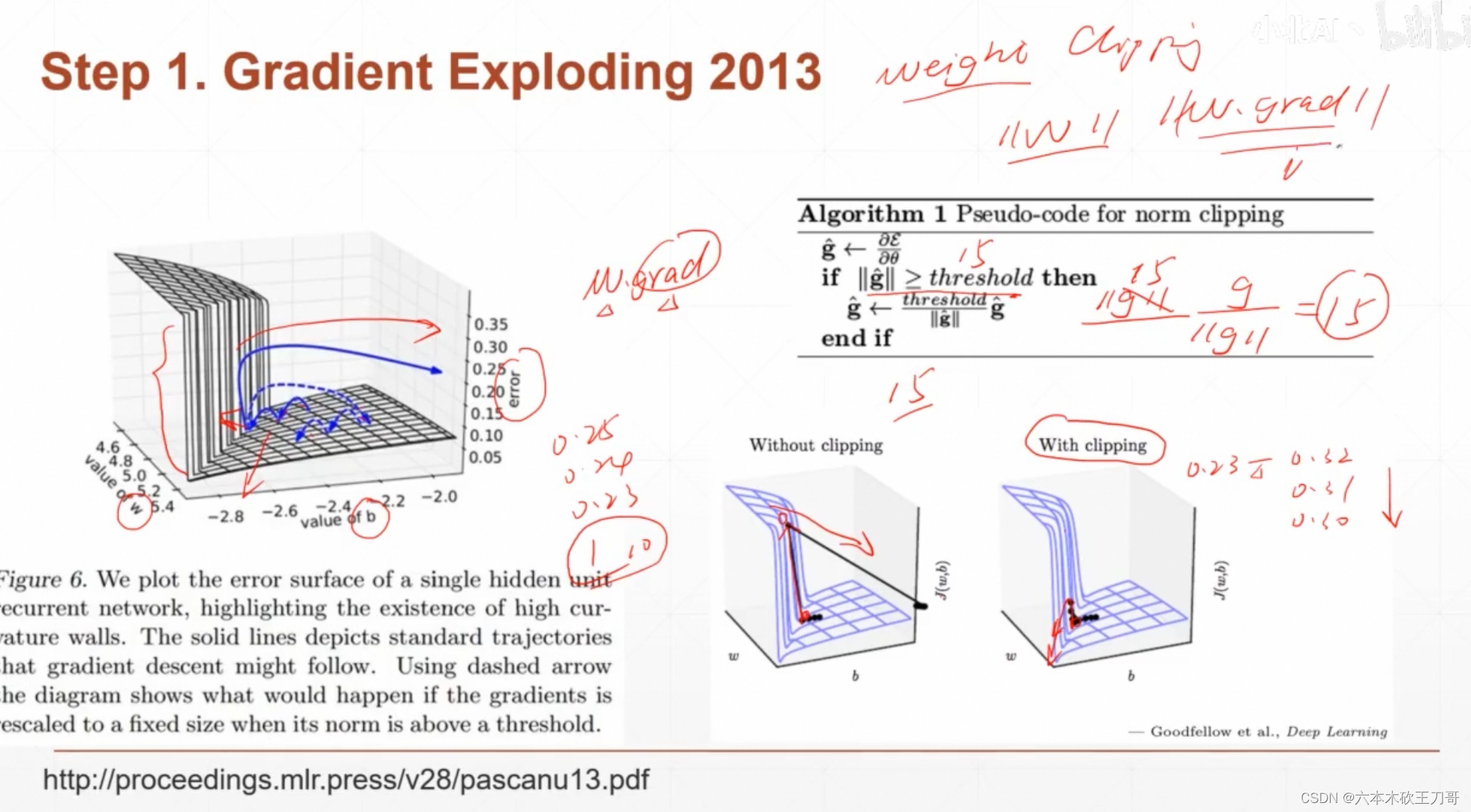
解决梯度爆炸，可以做一个梯度clipping，如果朝某一个方向更新过大的话，会导致权重变化很多，解决的方法就是设定一个threshold，如果超过这个阈值，就让当前这个方向的更新大小变成这个阈值，虽然方向是不变的，但是更新的大小减缓了。

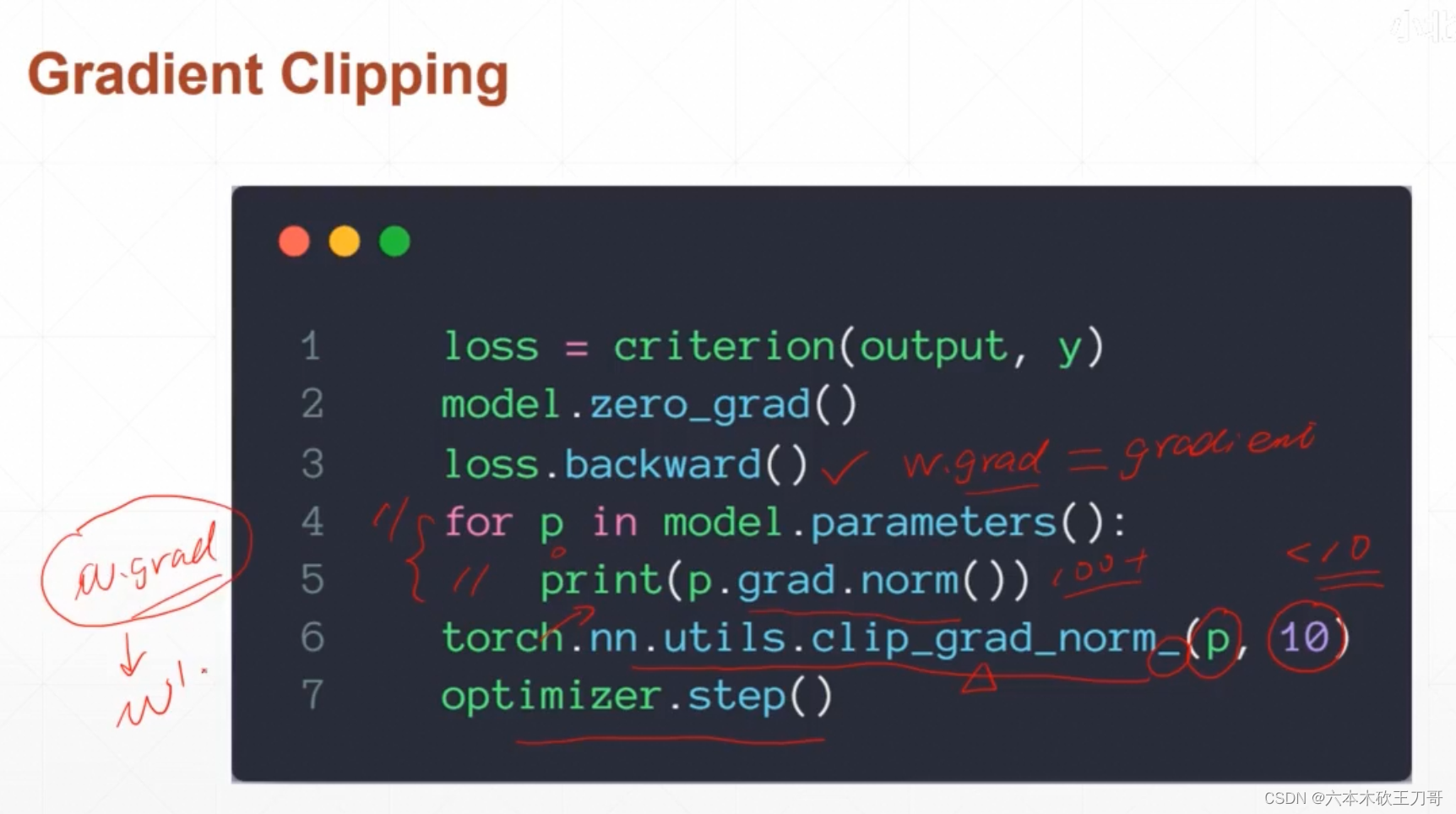
代码中，需要对每一个参数梯度做一个修改，其中第六行是要缩进到for循环内部的，这里的意思就是先对参数的梯度做修改，减小到阈值范围之内，然后才能经过step更新每一个w参数。

22. LSTM原理

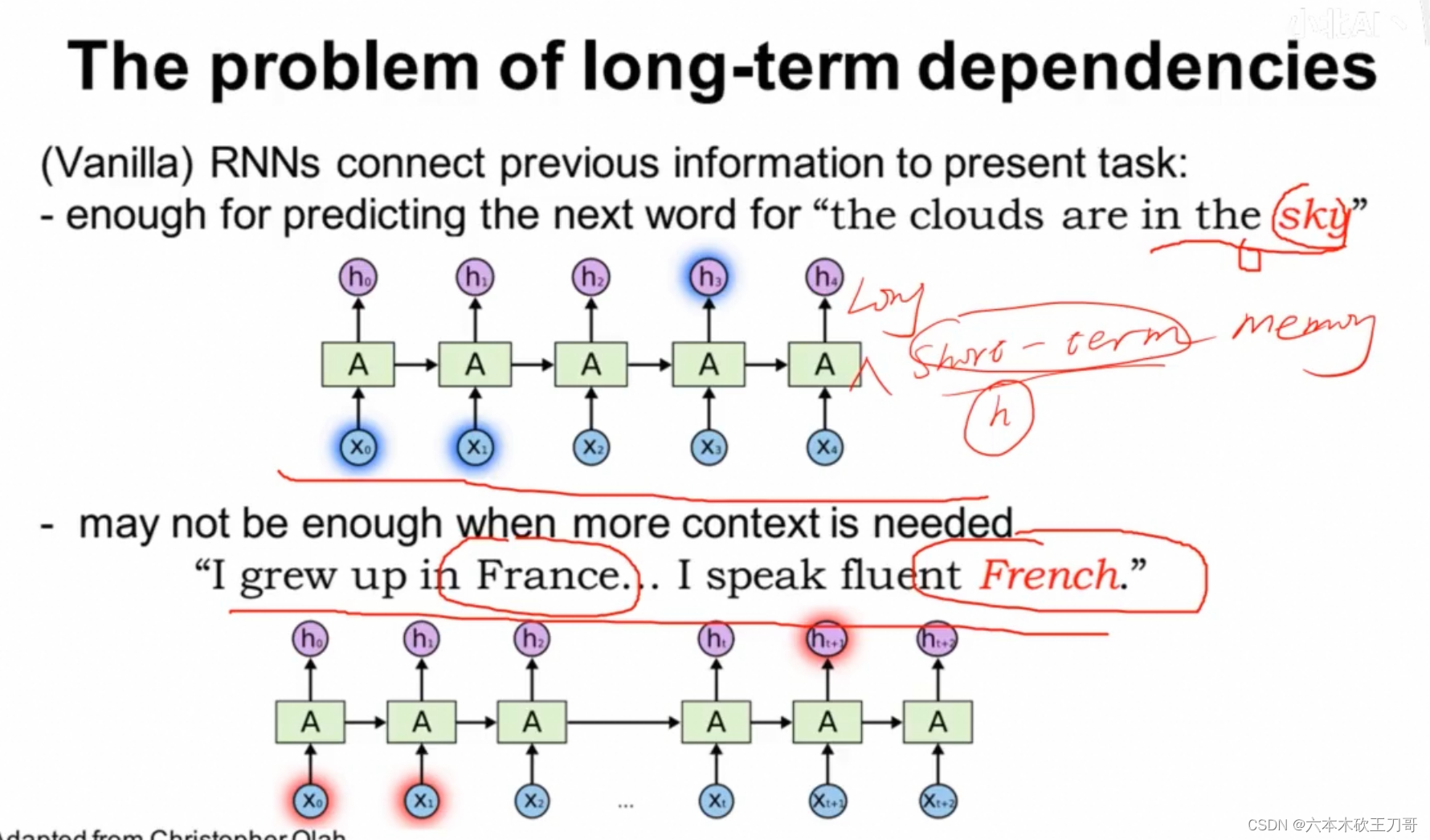
RNN只能处理很短距离的记忆，所以叫short-term，而LSTM可以很好处理长序列Long term

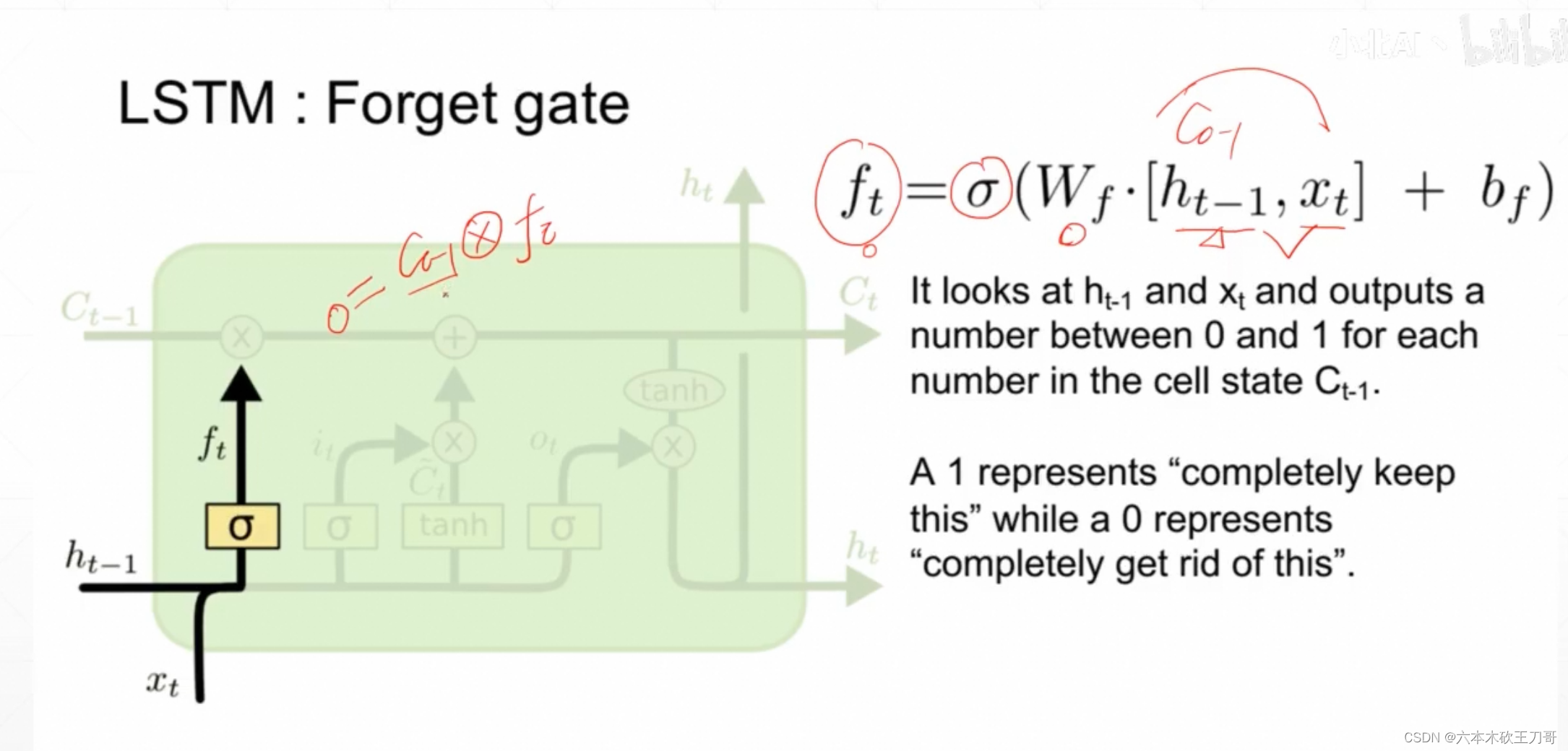
第一个门是遗忘门，输入是ht-1和xt，经过参数相乘和Sigmoid函数之后，会得到一个ft，这个ft乘上Ct-1决定了之前的memory能保留或者遗忘多少，1就是完成保留，0就是完全遗忘

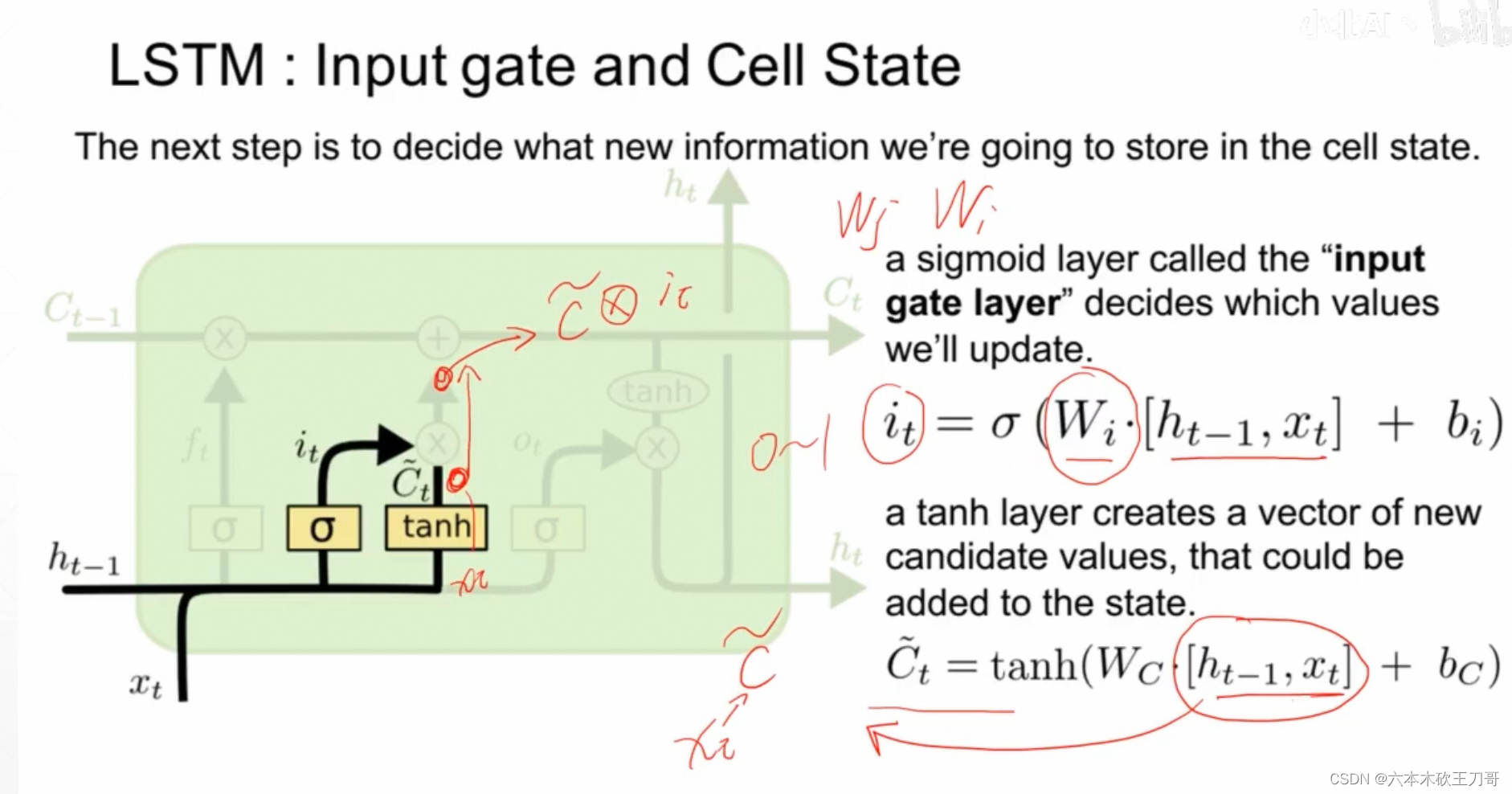
输入门it，其中计算it的Wi矩阵以及上面的W矩阵都是我们要通过反向传播学习的参数，决定这些信息需要保留和输入多少。新的信息Ct乘上开度it就得到了过滤后的新信息。

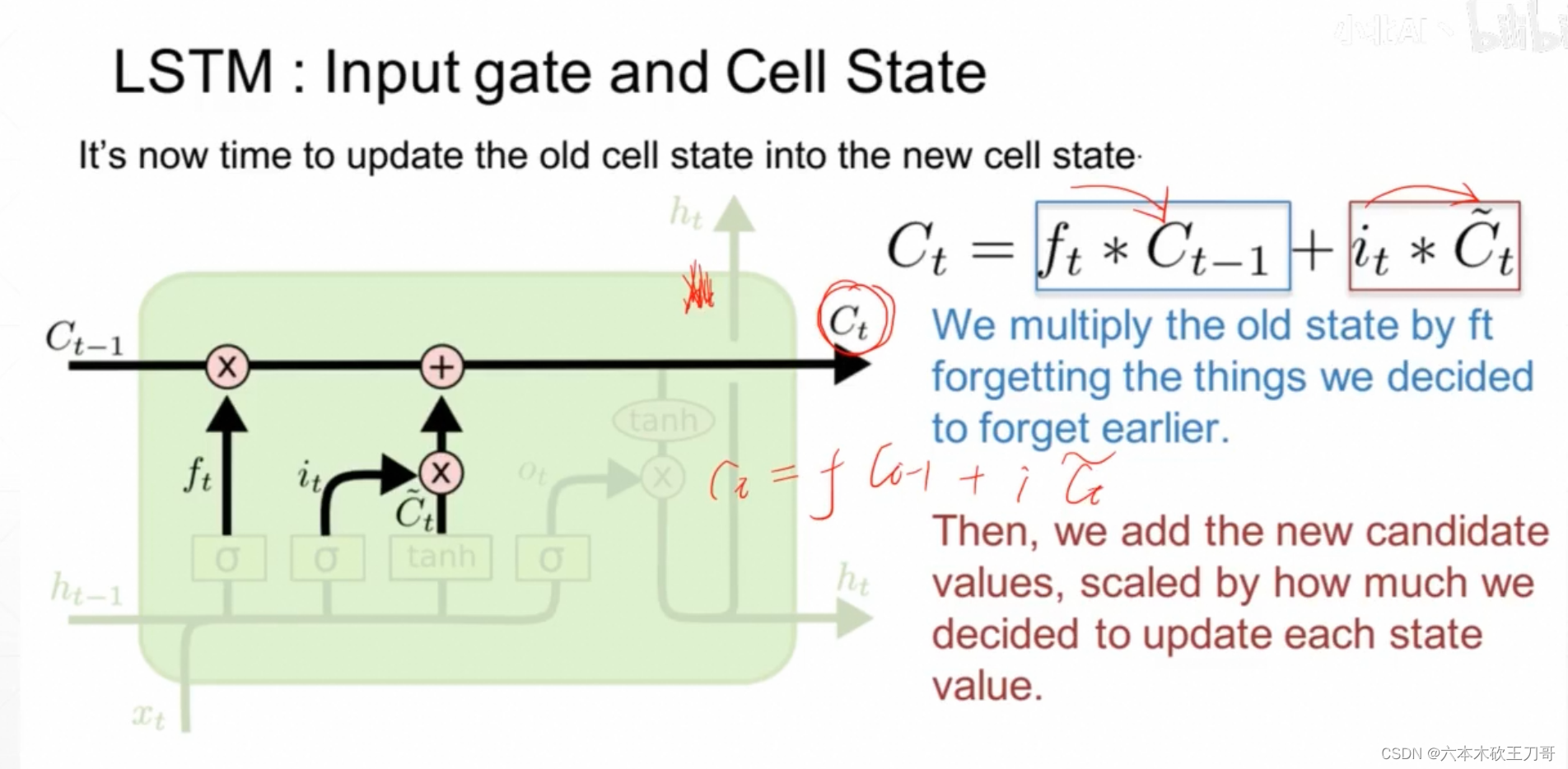
经过遗忘门和输入门，就得到过滤后的历史信息和过滤后的新信息，然后经过简单的相加就可以获得新信息memory Ct

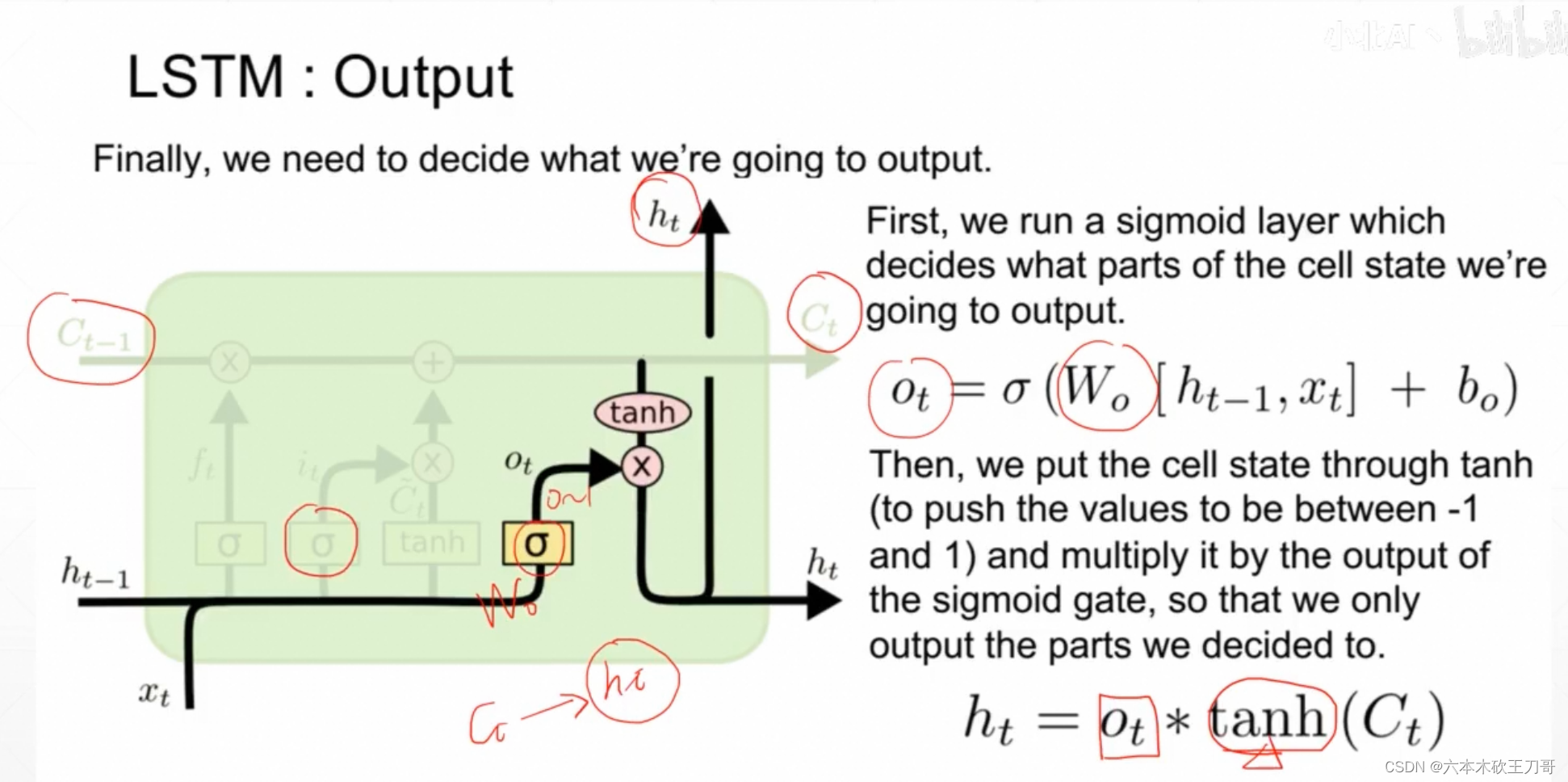
 最后一个门是输出门，需要计算ht，同样是之前的xt和ht-1乘上Wo参数矩阵，再经过Sigmoid函数得到一个出度，然后与Ct经过tanh相乘得到ht，也就是说memory会有选择的输出到ht上

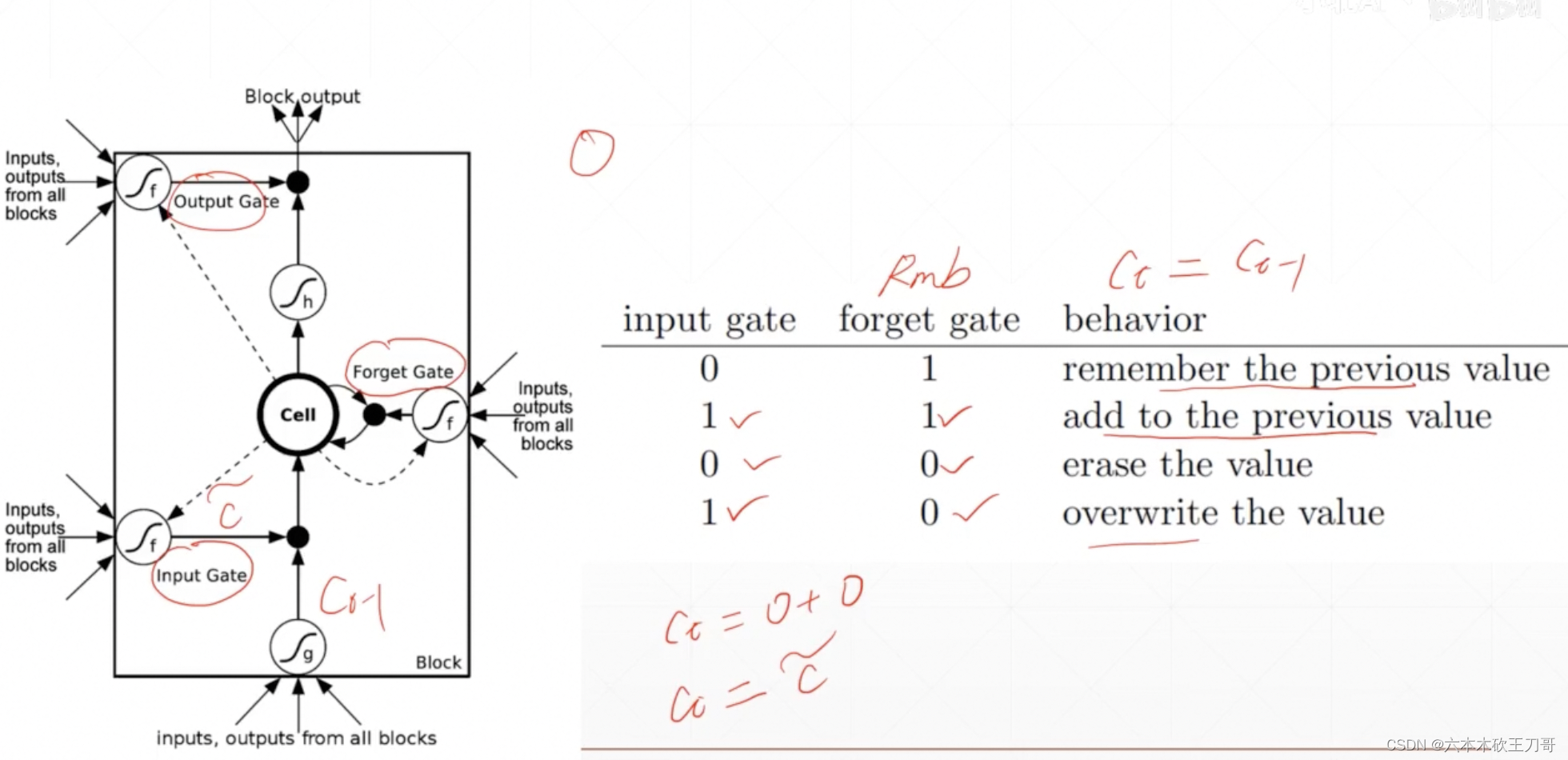
换一种方式去理解LSTM的遗忘门和输入门

为什么能解决梯度弥散问题。因为计算梯度公式的时候，之前的RNN会出现W的k次方这种情况，但是LSTM的梯度公式中会发现都是一些项的累加，累加的结果就不会出现某个项特别大的情况。另外一种理解就是RNN更新的时候都要经过Whh，但是LSTM中间有个类似ResNet的反馈，这样就使得Ct-1对Ct求导接近1（？）

23. LSTM代码

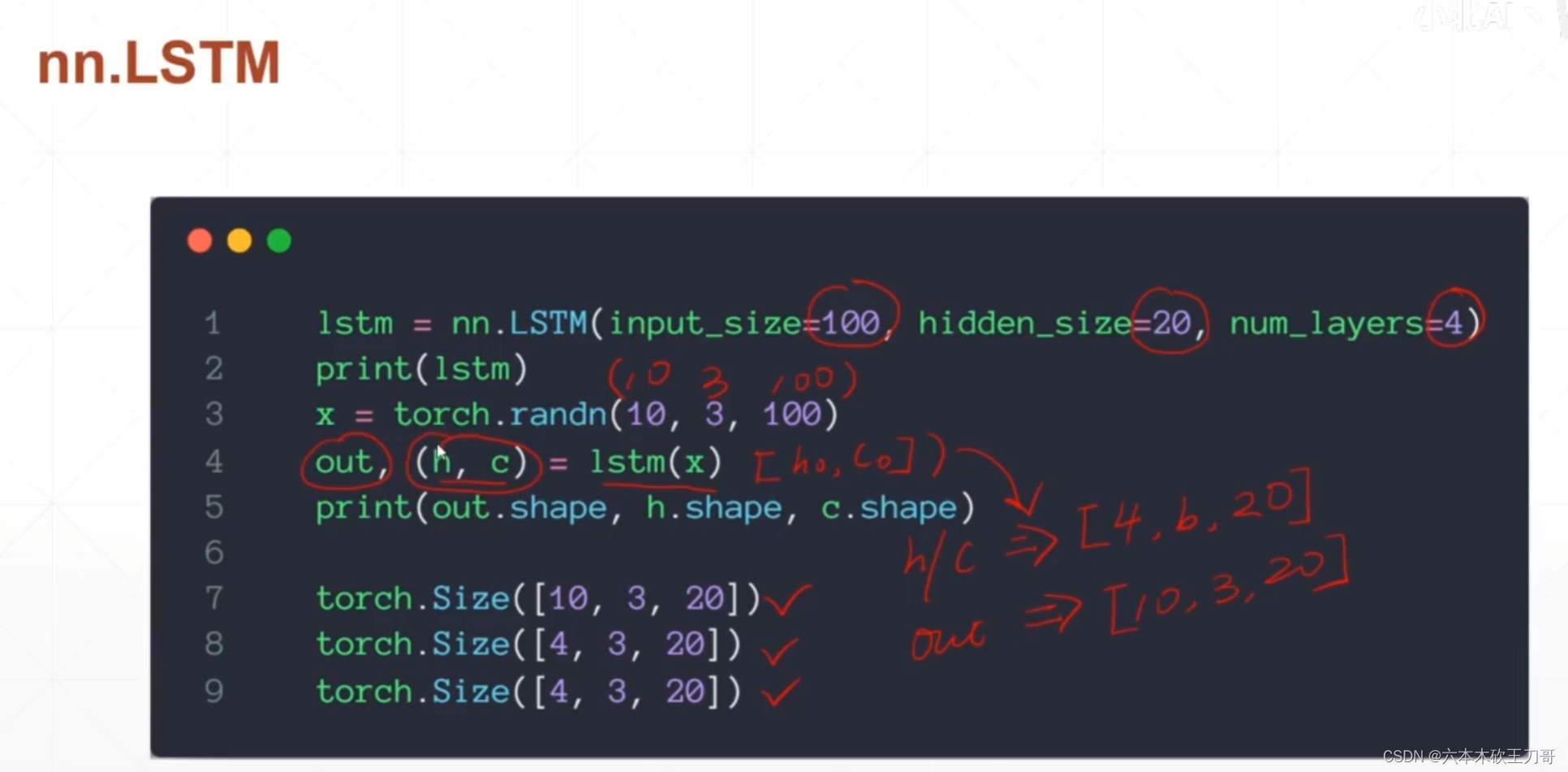
对于LSTM来说，Memory变成了C而不是RNN中的h，所以输入的参数和RNN的参数是一样的，并且C和h的维度是一样的

对于前向计算来说，唯一和RNN不同的就是输入和输出不再只有h，而是有C和h的集合

代码的相关推导，这里省略掉了初始化全为0的h和C

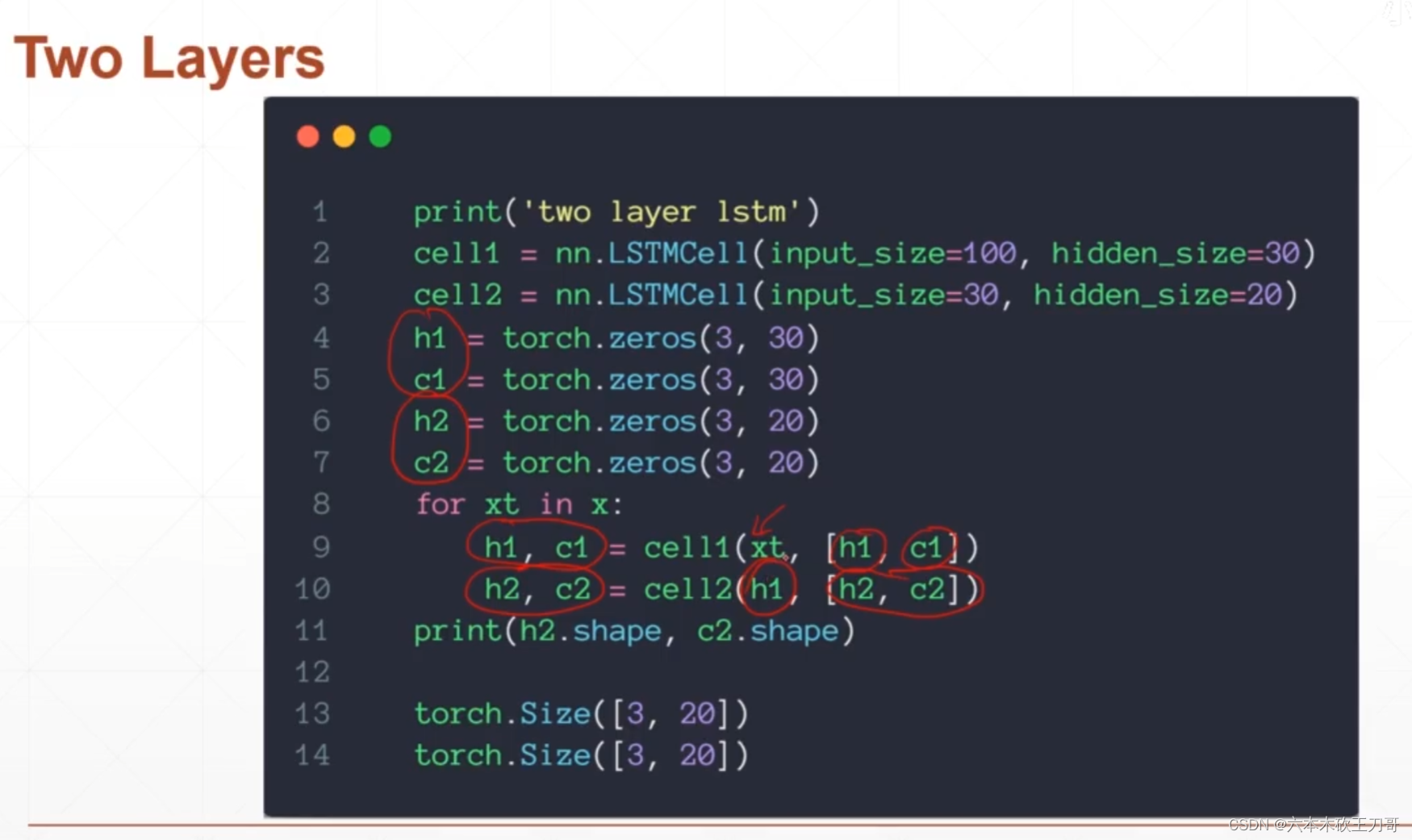
对于双层的LSTM，唯一不同的地方就是第二层单元输入不再是xt，而是ht