背景知识:
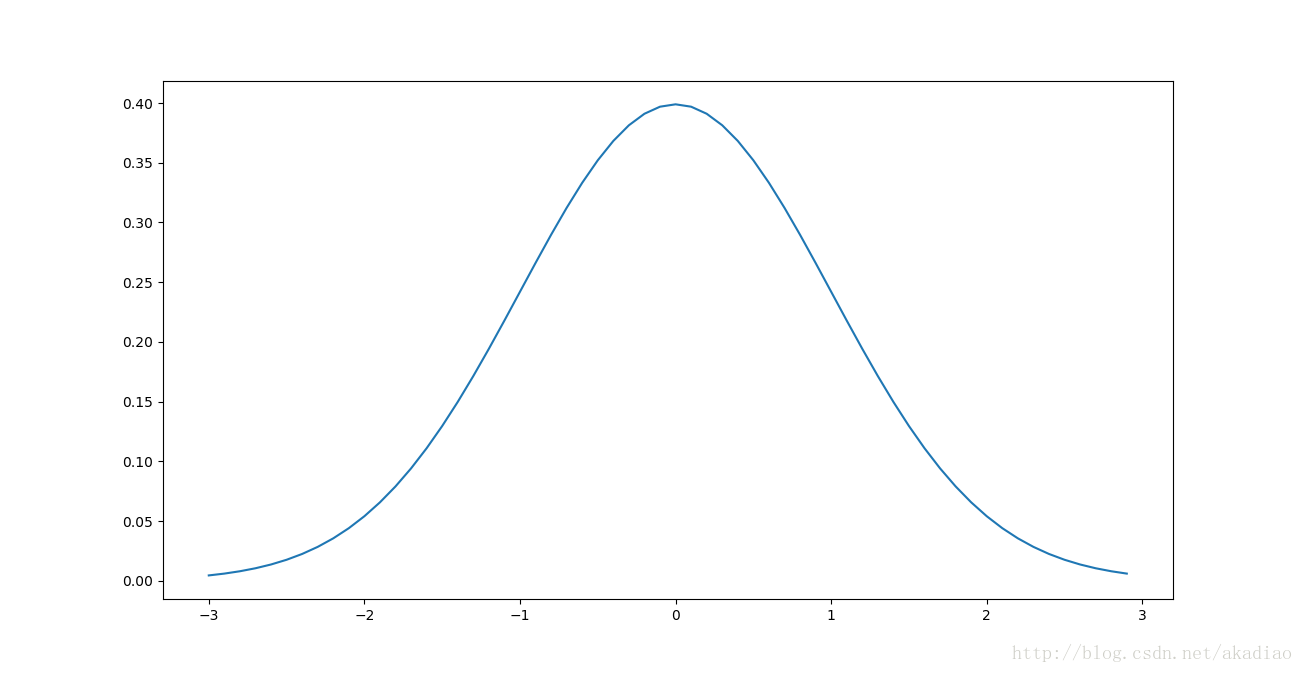
高斯分布:
f(x)=12π√σexp(−(x−μ)22σ2)
使用标准高斯分布对权重和偏向进行初始化
问题:会导致学习速度慢
根据独立标准高斯分布变量来选择权重和偏置,
μ=0
,
σ=1
标准高斯分布概率密度函数曲线:
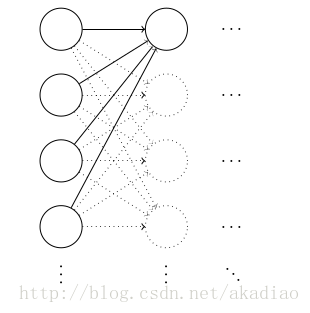
假设神经网络有1000个输入,并使用标准高斯分布初始化了连接第一个隐藏层的权重,现在只看该层的连接权重:
该层神经元的输入
z=∑jwjxj+b0
假设使用的输入x,一半的输入神经元值为1,其余为0,则
∑jwjxj
就是500个标准高斯分布的随机变量的和.所以:
E(∑jwjxj)=0
D(∑jwjxj)=500×1=500
可得:
μ=E(z)=E(∑jwjxj+b0)=0
σ2=D(z)=D(∑jwjxj+b0)=500×1+1=501
则该层神经元的输入z的概率密度函数为:
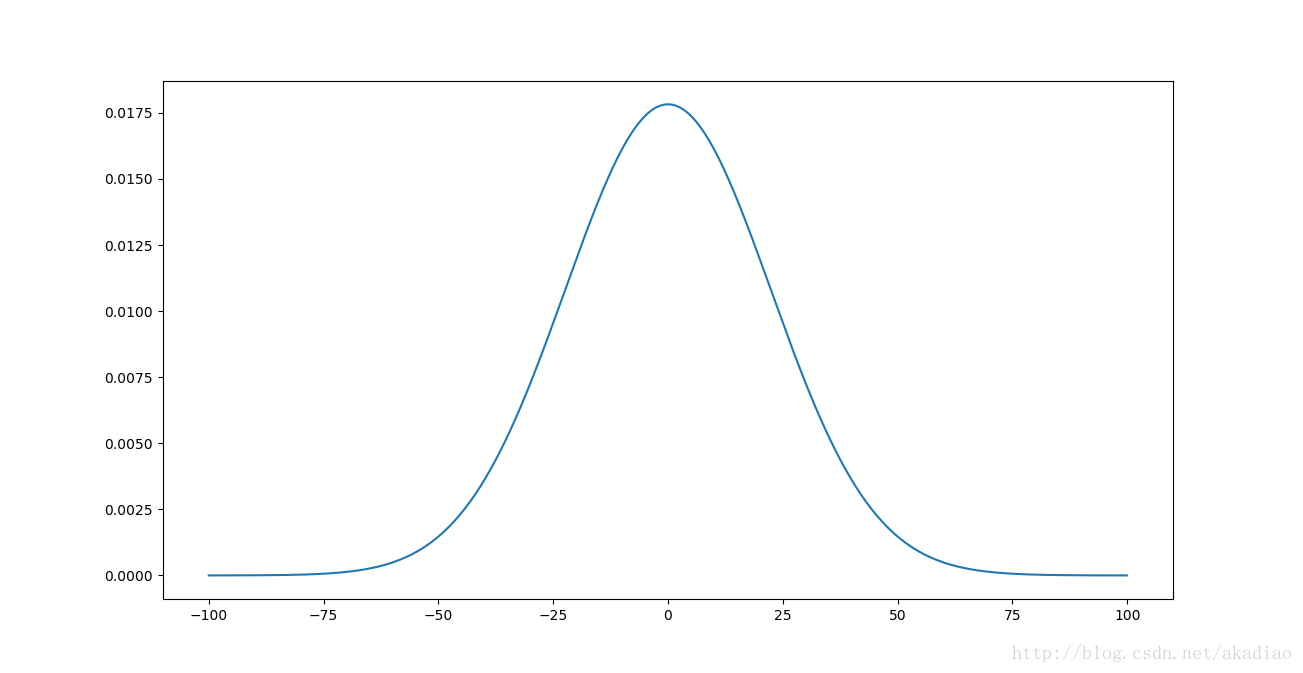
f(x)=12π×501√exp(−x22×501)
概率密度函数曲线:
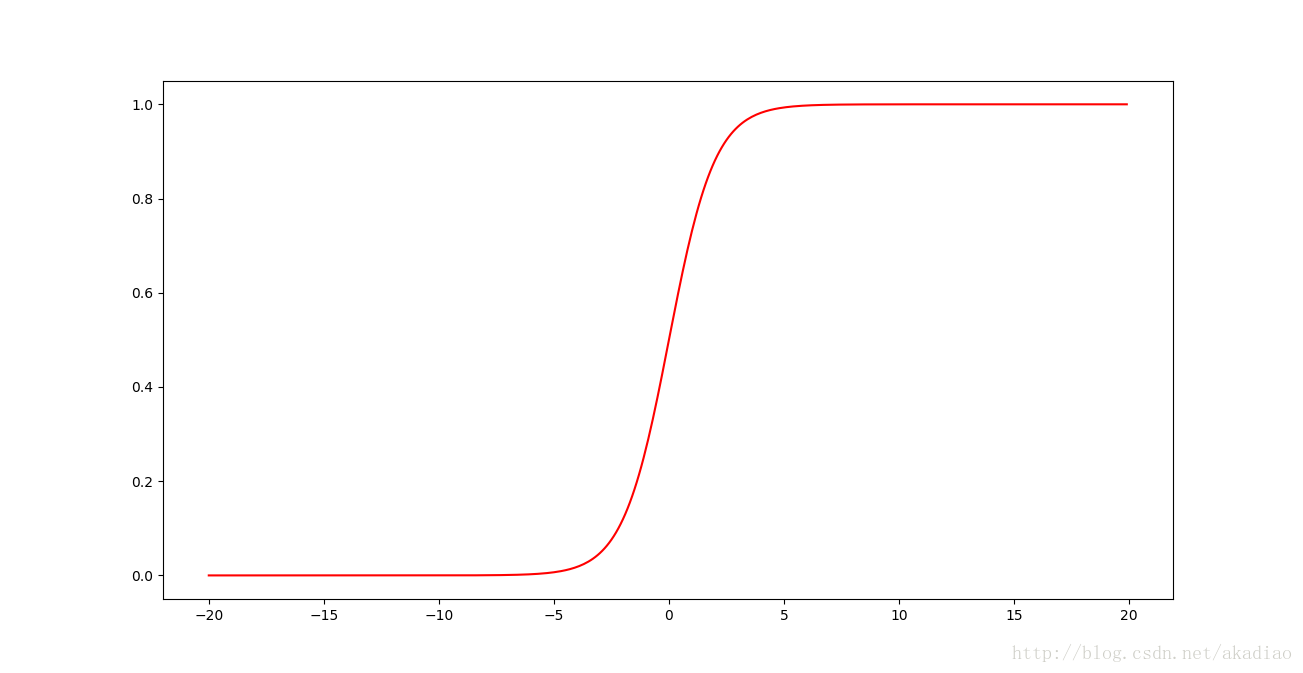
可以看到z有一个非常宽的高斯分布,z有很大的比例会分布在|z|>>1的区域,即z>>1或z<<-1.此时由激活函数 σ() (采用sigmoid函数)的图像可以看出:
隐藏神经元的输出 σ(z) 就会接近0或1,使隐藏层神经元达到饱和.此时对神经元权重进行微小调整只能给神经元的激活值带来非常微弱的变化.结果,在进行梯度下降算法时会导致神经网络学习缓慢.
code2中使用标准高斯分布对权重和偏向进行初始化:
# 使用均值=0 标准差=1的高斯分布,对权重和偏向进行初始化
def large_weight_initializer(self):
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])]
改进方法
使用 μ=0 σ=1nin√ 高斯分布的随机值,对权重和偏向进行初始化
此时
nin=1000
即
σ=11000√
仍假设输入为500个1和500个0,该层神经元的输入
z=∑jwjxj+b0
所以:
E(∑jwjxj)=0
D(∑jwjxj)=500×11000=0.5
可得:
μ=E(z)=E(∑jwjxj+b0)=0
σ2=D(z)=D(∑jwjxj+b0)=500×11000+1=1.5
则该层神经元的输入z的概率密度函数为:
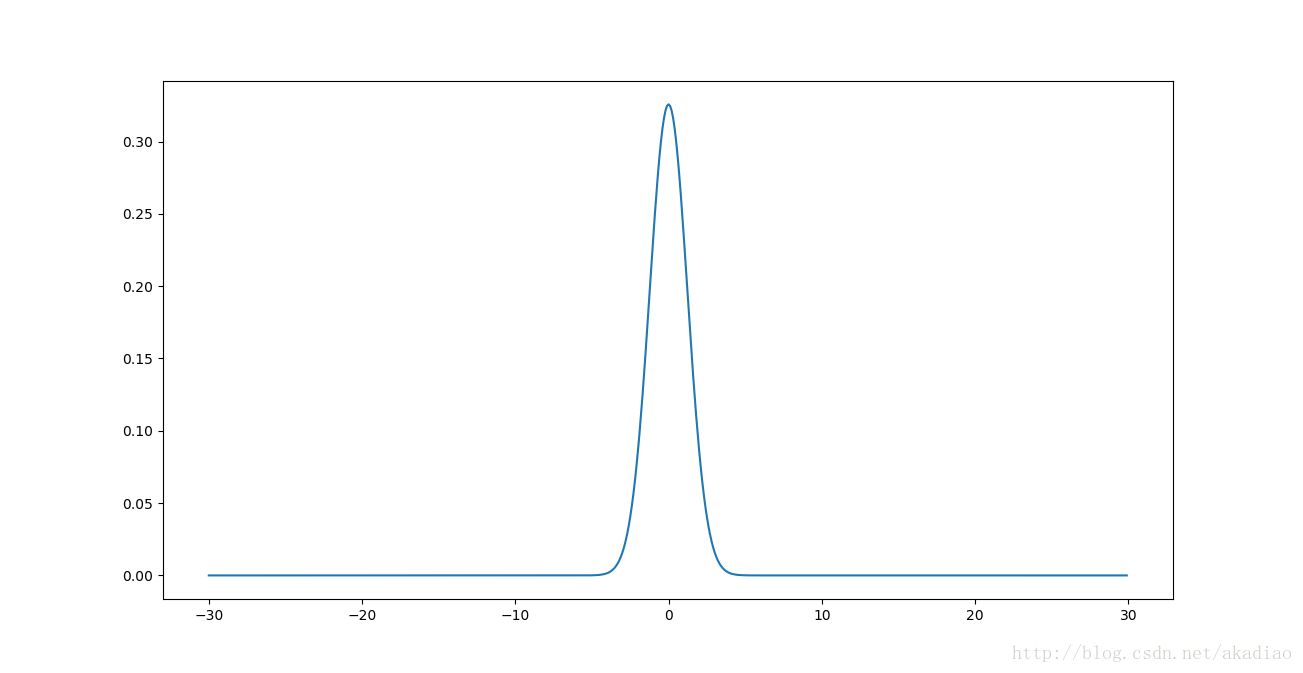
f(x)=12π×1.5√exp(−x22×1.5)
概率密度函数曲线:
可以看到z有一个非常窄的高斯分布.
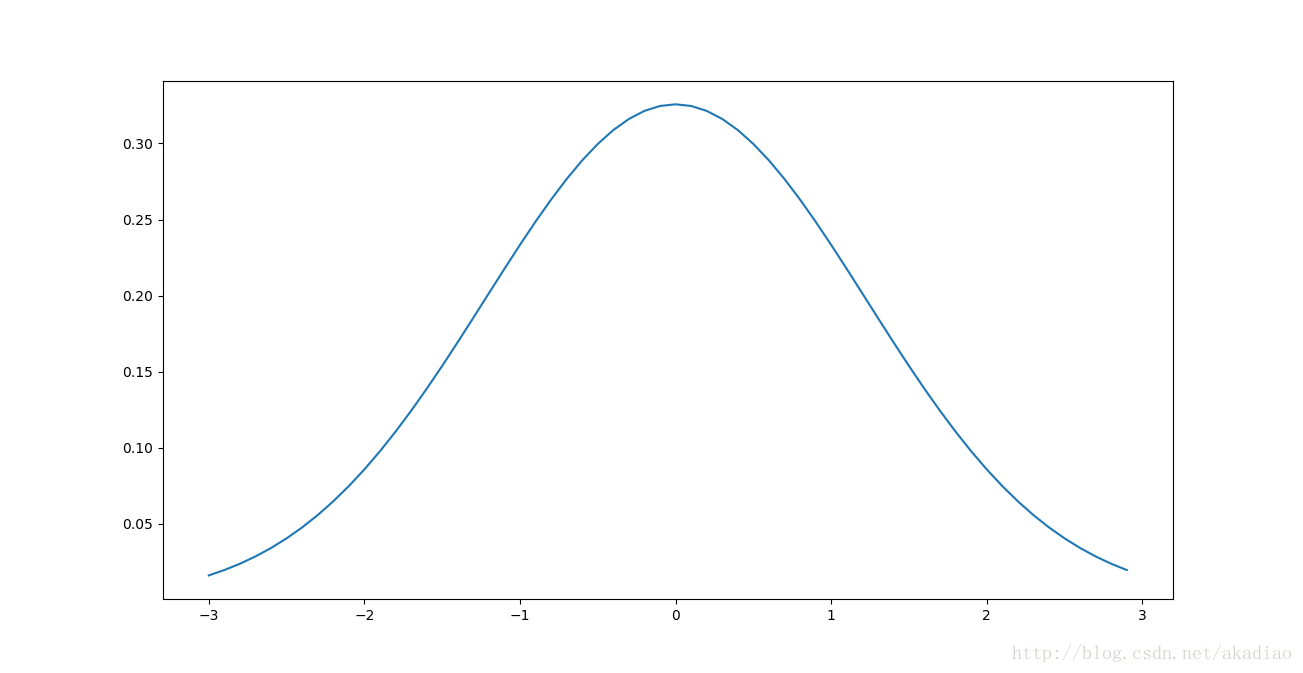
将横坐标拉伸可以看到:
大部分z的分布集中在-1到1之间,避免了使隐藏层神经元达到饱和,由激活函数图像可以看到:
在-1到1区间上 σ(z) 的斜率非常大,对神经元权重进行微小调整能给神经元的激活值带来非常明显的变化,解决了神经网络学习缓慢的问题.
code2中使用 μ=0 σ=1nin√ 高斯分布的随机值,对权重和偏向进行初始化
# 从正太分布(均值=0,标准差=1/sqrt(n_in))随机赋值,对权重和偏向进行初始化
def default_weight_initializer(self):
# 第一层为输入层不设置偏差,从第二行开始
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
# 在同一个神经元的权值的平方根的平方根上用高斯分布平均0和标准偏差1初始化每个权值
self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])]