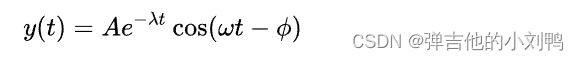动画系统里的临界阻尼与MotionModel

参考：spring-roll-cal
参考：Motion Matching 中的代码驱动移动和动画驱动移动
参考：游戏开发中的阻尼器和阻尼弹簧
参考：Damping
参考：The Art of Damping
参考：UE4中的阻尼弹簧平滑

介绍

此篇文章旨在处理游戏运行时，该如何把玩家的输入转换成平滑的曲线，介绍此篇文章之前抛出几个问题：

玩家的输入，怎么转换成人物模型的速度、转向速度、加速度等参数
怎么理解Damping这个变量
什么是阻尼、临界阻尼与过阻尼，什么是阻尼系数
什么是惯性化插值
如何根据带阻尼的弹簧运动模型，转换成对应的用于插值的Damper代码？
如何理解Motion Matching代码里面Daniel Holden写的Damper函数

关于Damping与Damper

damping, in physics, restraining of vibratory motion, such as mechanical oscillations, noise, and alternating electric currents, by dissipation of energy. Unless a child keeps pumping a swing, its motion dies down because of damping. Shock absorbers in automobiles and carpet pads are examples of damping devices.

Damping在物理学的解释是对vibratory motion(振动运动)的限制，Damper可以翻译为阻尼器，阻尼器（英语：shock absorber 或 damper）是一种利用阻尼特性来吸收或抑制冲量，藉以减缓力学振动及消耗动能的机械或液压装置。大部分的阻尼器都是以黏壶（dashpot）的形式，透过黏滞流体的阻尼来吸收或抑制冲量。shock absorber的翻译会比阻尼器更好理解，其实就是利用弹簧实现的减震器，如下图所示：
在这里插入图片描述

Damper的机制就是使物体位移曲线变得平滑，比如上图的摩托，没有减震器，车座位的抖动幅度就会很快，而且抖动速度也会从静止状态下的0迅速变大，而Damper就能减慢这个抖动的过程。在游戏里，Damper的作用是类似的，它可以在动画、物理等领域减少位移的突变，实现更自然的效果，其实就是起到渐变插值的作用

使用弹簧的阻尼平滑系统

先通过上面这篇文章，了解以下几点：

Damper在物理意义上是怎样的
什么是阻尼、临界阻尼与过阻尼，什么是阻尼系数

没有阻力的弹簧运动
理想情况下，没有任何阻力的弹簧运动是一个标准的简谐运动(就是类似sin或cos的三角函数)，运算逻辑为，基于dx/dt = v，dv/dt = a，再加上弹簧的胡克定律，力总与运动相反，可以得到弹簧的运动公式：
在这里插入图片描述

带阻力的弹簧运动
Dampe的在物理意义上就是给弹簧添加一个与弹簧速度方向相反的力，其大小与弹簧速率成正比，（可以想象是总有一个力在反方向阻碍自己的运动，而且运动速度越快，阻碍的力越大），然后弹簧本身会受到一个与当前位移反向的力-kx，，其运动模型会下面是后续的方程：
在这里插入图片描述
解释一下这里的参数，A是常数，代表弹簧的振幅，t表示时间，最后面的符号应该也是角度常量，剩下的数据有：

它是弹簧的劲度系数与弹簧质量的比的平方根，还有：

这玩意儿就叫阻尼比，它的值从大到小排列，可以分为四种情况：

无阻尼(undamped)：阻尼比为0，相当于没有能量减弱，弹簧可以一直做简谐运动
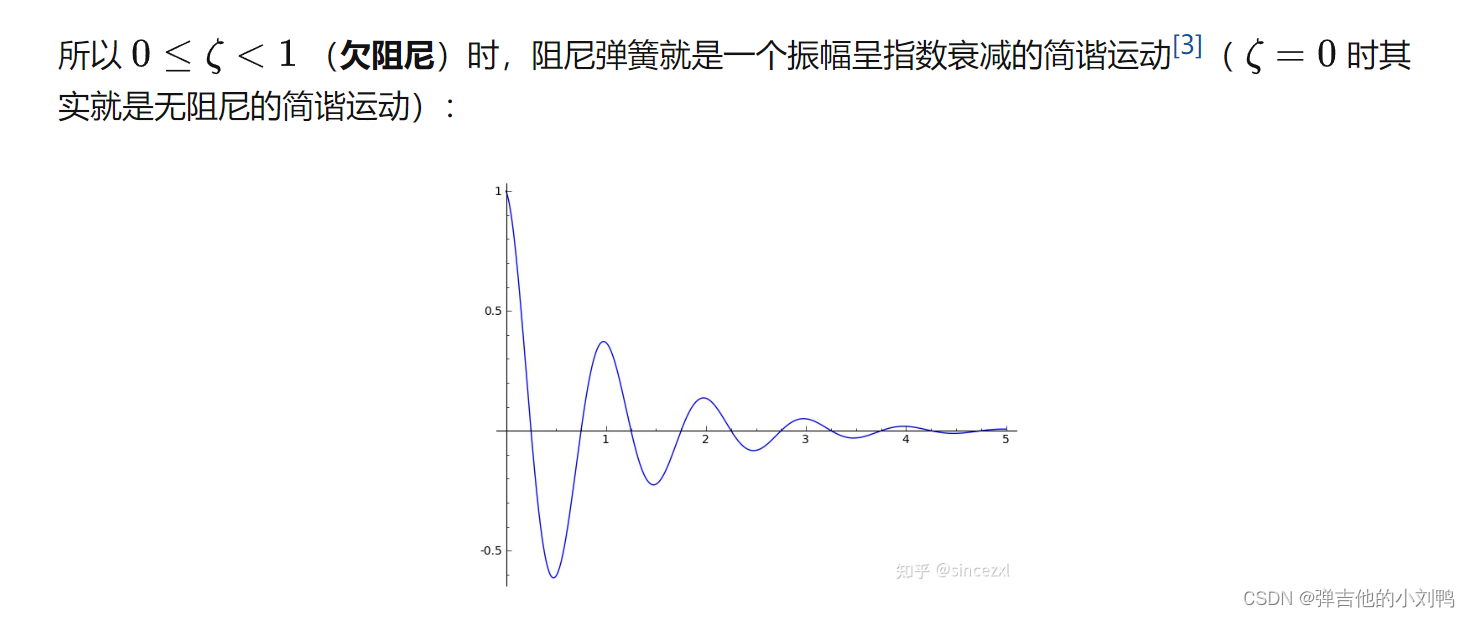
欠阻尼(underdamped)：阻尼比为(0,1)，(欠阻尼其实也算包括无阻尼)，振幅呈指数衰减的简谐运动
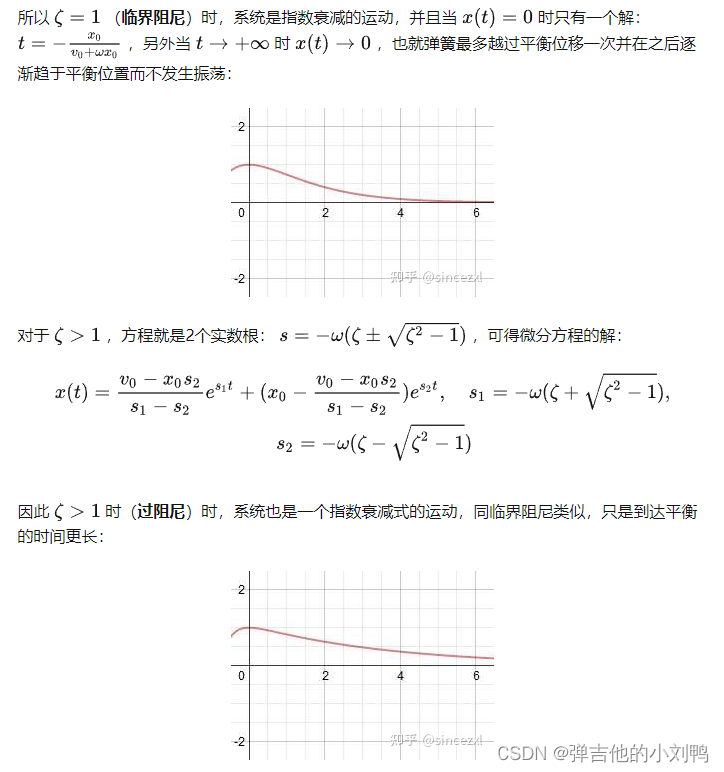
临界阻尼(critical damping)：阻尼比为1，振幅呈指数衰减，但不是简谐运动，不会越过平衡位
过阻尼(overdamped)：阻尼比大于1，系统也是一个指数衰减式的运动，同临界阻尼类似，只是到达平衡的时间更长：

关于Halflife

In the context of a spring-mass system, critical damping is a type of damping that results in the fastest possible decay of oscillations without overshooting the equilibrium position.
The half-life in critical damping is the time it takes for the amplitude of the oscillation to decrease to half of its initial value. It is determined by the equation:
t_half = ln(2)*m/b
where t_half is the half-life, m is the mass of the object attached to the spring, and b is the damping coefficient.
Note that this formula applies to the general case of critical damping and is not specific to any particular function.

也就是从当前距离，缩短到当前距离的一半需要的时间，也是一个物理波上的概念，如下所示，带阻尼的弹簧的运动公式为：
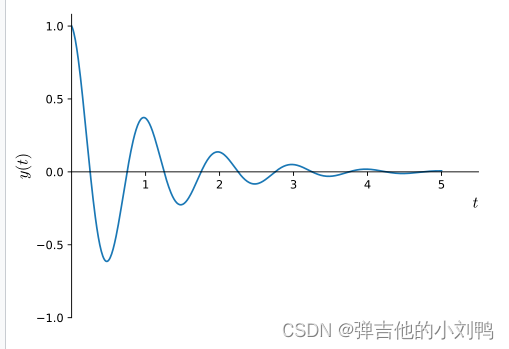
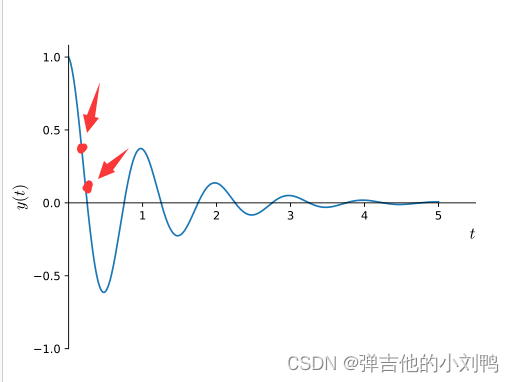
在这里插入图片描述
这是个周期为2PI/w的运动，表现为振幅不断减少的cos余弦运动，大致如下图所示：

在这里插入图片描述
额外解释一下，在临界阻尼和过阻尼情况下，可能只有一个周期(可能不到一个周期)的余弦波函数

那么什么是halflife呢，它指的是弹簧的振幅从开始的A，变成A/2所用的实际，这里令函数的振幅部分为A/2，则有：

e ^ (- λ * t) = 0.5
=> t = ln(2) / λ

可以看出，当时间t为ln(2)/ λ，运动的振幅减少到原本的一半，此时的t称作半衰期，英语叫halflife

转化阻尼弹簧模型到插值Damper函数

这个阻尼弹簧的运动公式求解其实挺简单明了的，重难点在于如何根据这个阻尼弹簧的运动公式，写出实际插值的Damper函数，更准确的是，如何理解别人写的Damper函数，这里的难点如下：

如果想让插值在固定时间内完成，应该怎么设计函数？
弹簧公式里的未知参数有：ω、λ和φ，这种参数怎么让调用者理解？
上面求出的公式是X(t)和t，变量是t，结果是位移，它的求解环境很理想化，实际的函数调用没有这么理想化

关于最后一点，额外解释一下，为什么上面的函数很理想化。因为这里需要一个起始插值的环境，记录下起始的时间T0，和其实目标点和当前点的距离作为振幅A，然后根据之后帧的时间Tx，算出t = Tx - T0，然后带入公式算出此时的X值，有点类似于线性插值的这种：

currentX = lerp(0, 1, accumulatedTime / TotalTime);

但是实际插值的时候应该是没有t这个持续改变的变量，每次函数调用都是一次单独的插值。那么有人可能会觉得，每次函数插值都当单独的一次插值一样不行吗，这样是不行的，因为这样，就不再满足原本的调用条件了，因为相当于每次调用的初始振幅都是新的值，这个运动波形也不再是余弦波。

其实此时的数学问题变成了：已知弹簧运动的一些参数，以及当前点的坐标和速度，预测deltaTime之后的点的坐标和速度，如下图所示，需要根据左边点的信息，预测deltaTime之后右边点的信息：
在这里插入图片描述

先来归纳一下游戏里的一般插值函数，也是最简单的插值函数，函数如下：

lerp(float begin, float end, float alpha);

虽然这是个线性插值函数，但是它用作插值，是一个指数衰减的曲线，如下图所示，这里的初始y值是目标点到起始点之间的距离：

如果是这么调用，那么是线性的：

currentX = lerp(0, 1, accumulatedTime / TotalTime);

如果是这么调用，那么不是线性的，只是一种插值手段

currentX = lerp(currentX, 1, alpha);//currenX起始为0

至于Critical Damping的函数代码，可以先参考下别人的写法：比如：

Unity里的SmoothDamp函数
UE里的SpringDamper函数
Daniel Holden里的Damper函数

比如Unity里的SmoothDamp函数：

// Unity的Damp函数
public static Vector3 SmoothDamp(Vector3 current, Vector3 target, ref Vector3 currentVelocity, float smoothTime, float maxSpeed = Mathf.Infinity, float deltaTime = Time.deltaTime);

Damper代码的设计

比如下面这种常见的Damper，代码如下所示：

float damper(float x, float y, float a)
{
	// x + a(y - x) 这么写看得更清楚
    return (1.0f - a) * x + a * y;
}

注意一下，虽然这个函数跟Lerp函数是一样的，但是它并不是线性插值，因为它调用的方法不同：

// 线性插值每次是这么调用的
lerp(x, y, accumulatedTime/TotalTime);

// 而damper是这么调用的, a是定值
lerp(x, y, a);

举个例子，输入的a代表插值程度，比如说我要从0到1，a为0.1，那么每次调用为：

x = 0, y = 1, a = 0.1 输出0.1
x = 0.1, y = 1, a = 0.1 输出0.1 + 0.09 = 0.19
x = 0.19, y = 1, a = 0.1 输出0.19 + 0.081 = 0.271

所以明显这个不是线性的，这个damper过程并不是线性衰弱的

但是这种Damper有一个缺点，当前的帧率会影响它衰减过程的用时，这里考虑再加一个dt的参数，表示deltaTime，此时的Damper函数改成了：

//  a代表插值进度, dt代表deltaTime
float damper_bad(float x, float t, float a, float dt)
{
    return lerp(x, t, a * dt);
}

// lerp函数抽了出来
float lerp(float x, float y, float a)
{
    return (1.0f - a) * x + a * y;
}

但这样也不好，因为dt是随帧率大幅度变化的，这里的damping值很难人为的去判断它应该是多少，a * dt很容易超过1，超过1意味着没有了任何Damper的效果，这意味着不同帧率的机器的a值还要设成不同的值

还有个更严重的问题，理论上，两个单独的dt时间变化后，和一次性2 * dt的时间变化和，Damper的改变量应该是相同的，这里可以看一下，假设x = 0, y = 1，dt为1，a为0.1。

对于两个单独的dt时间，那么：

第一次dt为1，a为0.1，输出0.1
第二次dt为1，a为0.1，输出0.1 + 0.09 = 0.19

如果dt为2，那么：

输出lerp(0, 1, 0.2) = 0.2

可以看到，同样的时间，多次调用Damper函数会表现出不同的结果，所以这里的Damper函数肯定是不被允许的。

现阶段的情况就是，我们试图找到一个合适的Damper函数，Damper函数的时间为t，值为X，相当于X(t)曲线，它需要满足以下条件：

函数与帧率相关，不同的帧率下，经过相同的时间，调用它得到的结果是相同的
函数的参数个数要尽可能少，参数更容易让人理解
函数要平滑，不仅是函数代表的位移要平滑，函数的导数代表的速度曲线也要平滑，甚至二阶导数代表的加速度曲线也要平滑，数学意义上讲，X(t)应该是一个可以无限微分的函数

这里直接给一个改进后的函数，具体的推导过程详见Spring-It-On: The Game Developer’s Spring-Roll-Call：

float damper_exponential(float x,  float goal, float damping,  float dt, float ft = 1.0f / 60.0f)
{
    return lerp(x, goal, 1.0f - powf(1.0 / (1.0 - ft * damping), -dt / ft));
}

这里的1 - ft * damping就是衰减速率，它表示经过时间后移向目标位置的距离比例。此时的平滑函数有两个值，一个是ft，一个是damping(类似于前面的t)。

此时的exponent_damper仍然有缺点:

不稳定的damper进化成了一个快速稳定
有俩变量，参数不够明了清晰

后面提出一种更好的办法，叫damper_implicit，我们将衰减速率设置为0.5，通过控制一个叫half-life的变量，这个变量大致表示移动到目标点一半距离消耗的时间，那么函数变为了：

float damper_implicit(float x,  float goal, float damping,  float dt, float ft = 1.0f / 60.0f)
{
    return lerp(x, g, 1.0f - powf(2, -dt / halflife));
}

通过改变衰减速率达成的效果完全可以通过改变halflife实现，但implicit damper虽然能够处理一些需求但它存在一个很严重的问题，那就是当目标位置快速发生变化时会产生运动的不连续，通过上面的视频可以看到当物体正向某一个方向移动时目标位置切到了反方向这时候就会发生运动突变

问题主要原因在于速度的不连续，无论之前的帧发生了什么damper始终是直接向目标位置移动的，我们看下应该如何修复这个问题.

Spring Damper

Spring Damper是文章里给出的最平滑的damper，基于上面的原理，添加两个参数：

stiffness: 趋势我们移向目标位置的速度
goal velocity：保证最后能够趋向于这个速度值，当该值很小时我们可以把它看成摩擦项负责减速

假设每帧的deltaTime为定值dt，那么第一次调用时，结果为

output = lerp(x, y, a * dt) =  (1.0f -  a * dt) * x + a * dt * y;

第二次调用时，结果为：

output = lerp((1.0f -  a * dt) * x + a * dt * y, y, a * dt) =  ((1.0f -  a * dt) * x + a * dt * y) * x + a * dt * y;

为了简化公式，设1.0f - a * dt为q，那么有：

// 第一次结果为
q * x + a * dt * y
// 第二次结果为
(q * x + a * dt * y)x + a * dt * y => q * x^2 + a * dt * xy + a * dt * y

关于Strafing

strafe在英语里有俩意思：

verb (used with object), strafed, straf·ing.
to attack (ground troops or installations) by airplanes with machine-gun fire.
Slang. to reprimand viciously.
verb (used without object) strafed, straf·ing.
(of a player character in a video game) to move sideways while keeping a target in view, rather than turning the body to face the character’s destination in a regular forward movement.

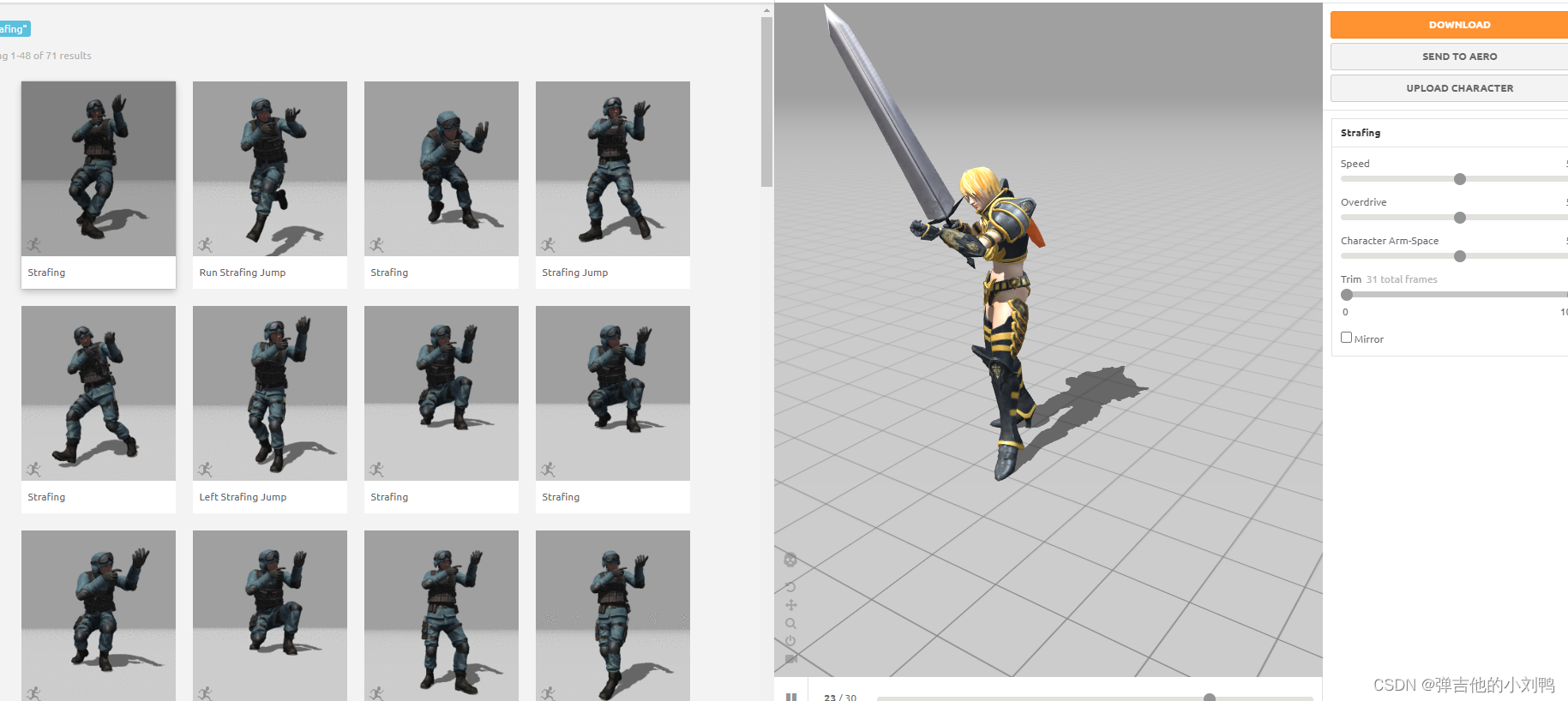
其实就是侧身看的意思，比如游戏里的strafing attack，如下图所示，就是侧身的动作，这些动作里，人物的朝向和Forward方向是不一致的：
在这里插入图片描述
不过我看了下，貌似还有一种说法，游戏里面的运动一般有两种：

人物的Forward始终跟移动的方向(相当于手柄的左摇杆方向)一致，这种貌似叫non-strafing动画，此时不需要后退动画、左右移动画等
人物的Forward始终跟视角方向(相当于手柄的右摇杆方向)一致，这种貌似叫strafing动画，此时会有后退动画，之狼、老头环这种游戏应该都用的此种模式