8.4 深度优先搜索(Depth First Search)算法
深度优先搜索(Depth First Search,DFS)是一种用于遍历或搜索树或图的算法,它从起始节点开始沿着一条路径一直向前直到达到末端,然后回溯到上一个节点,继续沿着另一条路径探索,直到所有节点都被访问过为止。DFS 使用栈(Stack)来存储待访问的节点。
8.4.1 深度优先搜索算法介绍
深度优先搜索(Depth First Search,DFS)是一种经典的图遍历算法,用于在图中搜索或遍历节点。DFS属于一种盲目搜索算法,没有启发式信息的辅助,而是通过深度优先的方式探索图中的节点。
1. 基本思想
- 从起始节点开始,访问一个节点后立即探索它的邻居节点,深入到最深的节点,直到到达最末端。
- 当无法再继续深入时(即当前节点没有未访问的邻居节点),回溯到上一个节点,继续深度优先搜索其他分支。
- 重复这个过程,直到遍历到所有节点或者达到搜索终止条件。
2. 实现方式
- 递归实现:DFS可以使用递归来实现,利用递归函数不断调用自身来实现深度优先搜索。
- 栈实现:DFS可以使用栈来实现,利用栈数据结构来模拟递归过程,手动维护遍历的状态信息。
下面是一个简单的深度优先搜索算法的伪代码实现:
procedure DFS(G, v):
stack S := empty stack
S.push(v)
while S is not empty:
current := S.pop()
if current is not visited:
visit(current)
mark current as visited
for each neighbor w of current in G:
if w is not visited:
S.push(w)在上述伪代码中,G 表示图,v 表示起始节点。在 DFS 过程中,首先创建一个空栈 S,然后将起始节点 v 入栈。然后,循环直到栈为空,从栈中弹出一个节点 current。如果 current 节点尚未被访问过,则对其进行访问并标记为已访问。然后,遍历 current 节点的所有未访问的相邻节点,并将它们入栈。最终,重复这个过程直到栈为空,所有节点都被访问过。
深度优先搜索算法的时间复杂度是 O(V + E),其中 V 是节点的数量,E 是边的数量。
8.4.2 寻找猫咪的最短路径
下面是一个使用深度优先搜索算法为猫咪寻找最短路径的例子,在这个例子中,使用一个二维列表来表示迷宫,其中0表示可通行的空格,1表示障碍物。假设在一个迷宫中,有一只可爱的猫咪迷失了方向,它想要从起始点(左上角)尽快找到出口(右下角),你能帮助它找到最短路径吗?
迷宫是一个由0和1组成的矩阵,其中0表示可通行的空格,1表示墙壁阻挡。猫咪只能水平或垂直移动,不能斜向移动,并且它不能穿过墙壁。请使用深度优先搜索算法来帮助猫咪找到最短路径,并将路径在迷宫中以红色线条标识出来。下面是迷宫示例(0表示可通行,1表示墙壁):
maze = [
[0, 1, 0, 0, 0],
[0, 0, 0, 1, 0],
[1, 1, 0, 1, 0],
[1, 1, 0, 0, 0],
[1, 1, 1, 1, 0]
]实例8-5:使用深度优先搜索算法为猫咪寻找最短路径(codes/8/ddfs.py)
实例文件ddfs.py的具体实现代码如下所示。
import matplotlib.pyplot as plt
def is_valid_move(maze, row, col, visited):
rows = len(maze)
cols = len(maze[0])
return row >= 0 and row < rows and col >= 0 and col < cols and maze[row][col] == 0 and not visited[row][col]
def dfs_shortest_path(maze, row, col, destination, visited, path, shortest_path):
if row == destination[0] and col == destination[1]:
shortest_path[:] = path
return True
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)] # 右、下、左、上
for dr, dc in directions:
new_row = row + dr
new_col = col + dc
if is_valid_move(maze, new_row, new_col, visited):
visited[new_row][new_col] = True
path.append((new_row, new_col))
if dfs_shortest_path(maze, new_row, new_col, destination, visited, path, shortest_path):
return True
visited[new_row][new_col] = False
path.pop()
return False
def find_shortest_path(maze):
rows = len(maze)
cols = len(maze[0])
start = (0, 0)
destination = (rows - 1, cols - 1)
visited = [[False for _ in range(cols)] for _ in range(rows)]
visited[0][0] = True
shortest_path = []
dfs_shortest_path(maze, 0, 0, destination, visited, [(0, 0)], shortest_path)
return shortest_path
def plot_maze_with_path(maze, shortest_path):
rows = len(maze)
cols = len(maze[0])
plt.figure(figsize=(cols, rows))
plt.imshow(maze, cmap='binary')
for i in range(len(shortest_path) - 1):
current_row, current_col = shortest_path[i]
next_row, next_col = shortest_path[i+1]
plt.plot([current_col, next_col], [current_row, next_row], color='red', linewidth=2)
plt.xticks(range(cols))
plt.yticks(range(rows))
plt.gca().invert_yaxis() # 反转y轴,使得坐标原点在左上角
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.title('Maze with Shortest Path')
plt.show()
# 示例迷宫
maze = [
[0, 1, 0, 0, 0],
[0, 0, 0, 1, 0],
[1, 1, 0, 1, 0],
[1, 1, 0, 0, 0],
[1, 1, 1, 1, 0]
]
shortest_path = find_shortest_path(maze)
if shortest_path:
print("Shortest path found:")
for row, col in shortest_path:
print(f"({row}, {col}) -> ", end="")
print("Destination")
plot_maze_with_path(maze, shortest_path)
else:
print("No path found!")上述代码的实现流程如下所示:
(1)首先,定义了一个迷宫,迷宫是一个二维列表,其中0表示可通行的空格,1表示墙壁阻挡。这个迷宫是一个5x5的矩阵,代表了猫咪可能迷失的区域。
(2)然后,使用深度优先搜索算法来帮助猫咪找到从起始点(左下角)到出口(右上角)的最短路径。首先定义了函数 is_valid_move 来检查机器人是否可以朝某个方向移动,然后使用深度优先搜索来找到最短路径。
(3)接着,定义函数plot_maze_with_path,用于在找到的最短路径上绘制了红色线条,以便清晰地看到猫咪应该走的路径。通过使用 matplotlib 库来绘制迷宫和最短路径,将最短路径以红色线条标识出来。
(4)最后,在主程序中调用相应的函数,传入迷宫信息,找到最短路径并将其绘制出来。这样,就完成了寻找猫咪最短路径的任务。
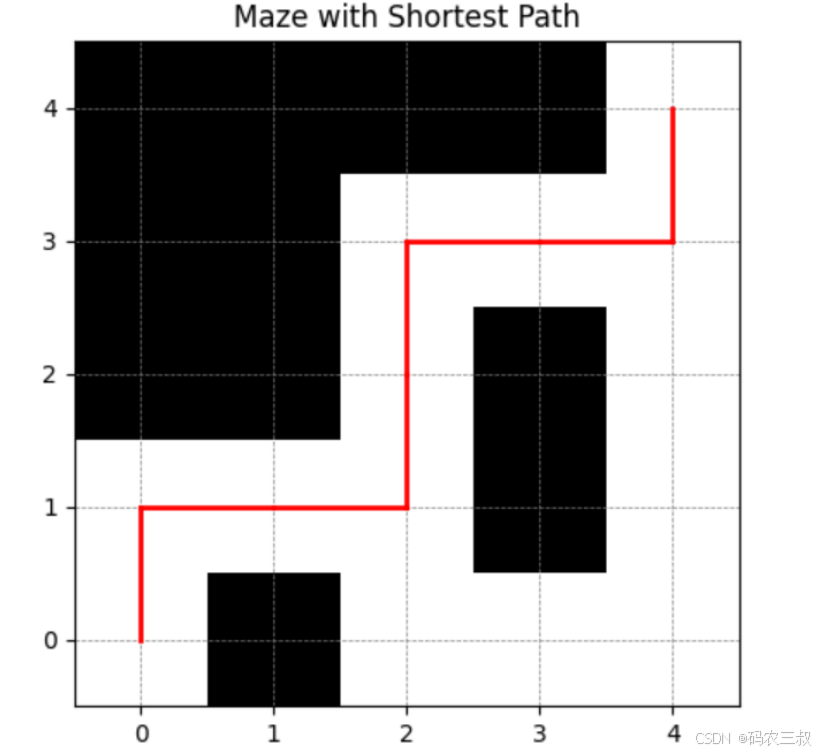
执行后会打印输出如下所示的路径信息,并绘制如图8-4所示的路径可视化图。
Shortest path found:
(0, 0) -> (1, 0) -> (1, 1) -> (1, 2) -> (2, 2) -> (3, 2) -> (3, 3) -> (3, 4) -> (4, 4) -> Destination图8-4 路径可视化图