图的邻接矩阵和邻接表表示

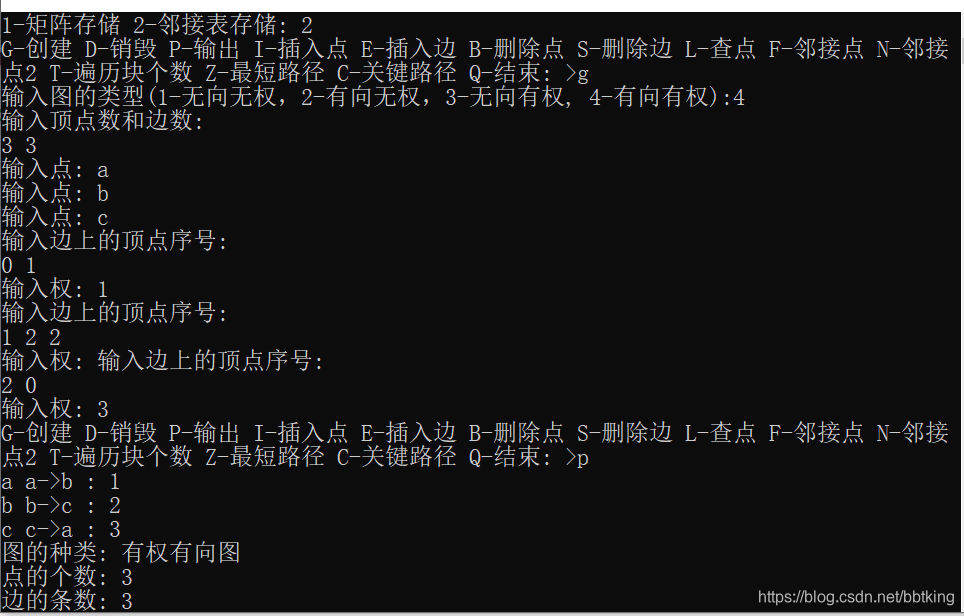
该图扩展到网络的功能，有最短路径和拓扑排序，关键路径功能，其中图分四种类型，存储方式为两种。
以下为运行结果
在这里插入图片描述
基类：
头文件Graph.h

#ifndef _Graph_h_
#define _Graph_h_




class GRAPH
{
	public:
		GRAPH();//构造 
		~GRAPH();//析构 
		
		int ReturnVert();//返回点的个数 
		int ReturnEdge();//返回边的条数 
		
		virtual void CreateMGraph()=0;//创建 
		virtual void DestoryGraph()=0;//销毁 
		virtual void PutoutGraph() const =0;//输出 
		
		virtual int LocateVertex( char v)=0;//返回顶点的下标 
		virtual char GetVertex( int i)=0;//返回下标为i的点的值 
		virtual string FirstAdjVertex( char v)=0;//v的第一个邻接点 
		virtual string NextAdjVertex( char v, char w)=0;//v的w后面的邻接点 
		virtual void InsertVertex( char v)=0;//插入点 
		virtual void DeleteVertex( char v)=0;//删除点以及相关边 
		virtual void DeleteEdges( char v, char w)=0;//删除边 
		virtual void InsertVertex( char v, char w)=0;//插入两点间的边 
		
		virtual void DFS( int i,bool vis[])=0;//从第i个点遍历,vis[]为标记数组 
		virtual int DFSTrave()=0;//遍历块的个数	
		
		virtual void Floyd(int t, int t1)=0;//两点最短路径 
		virtual void FloydPrintPath(int u,int v,int **path)=0;//输出路径过程 
		
		virtual int TopologicalSort()=0;//拓扑排序 
		virtual void CriticalPath()=0;//关键路径 
	
	protected:
		int numNodes,numEdges;//图的点，边 
		int kind;//种类 
};
#endif

Graph.cpp

#include <iostream>
using namespace std;
#include"Graph.h"

GRAPH::GRAPH(): kind(0),numNodes(0),numEdges(0)
{
}
GRAPH::~GRAPH()
{
}
int GRAPH::ReturnVert()
{
	return numNodes;
}
int GRAPH::ReturnEdge()
{
	return numEdges;
}

子类矩阵存储：
头文件MGraph.h

#ifndef _MGraph_h_
#define _MGraph_h_
#include "Graph.h"




class MGRAPH: virtual public GRAPH
{
	public:
		 MGRAPH();//构造 
		 ~MGRAPH();//析构
		 
		void CreateMGraph();//创建 
		void DestoryGraph();//销毁 
		void PutoutGraph() const;//输出 
		
		
		int LocateVertex( char v);//返回点的下标 
		char GetVertex( int i);//返回下标为i的点的值 
		string FirstAdjVertex( char v);//v的第一个邻接点 
		string NextAdjVertex( char v, char w);//v的w后面的邻接点 
		void InsertVertex( char v);//插入点 
		void DeleteVertex( char v);//删除点以及相关边 
		void DeleteEdges( char v, char w);//删除边 
		void InsertVertex( char v, char w);//插入两点间的边 
		
		void DFS( int i,bool vis[]);//从第i个点遍历 
		int DFSTrave();//遍历块的个数	
		
		void Floyd(int t, int t1);//两点最短路径 
		void FloydPrintPath(int u,int v,int **path);//输出路径过程 
		
		int TopologicalSort();//拓扑排序 
		void CriticalPath();//关键路径 
		
	protected:
		char *vexs; //存顶点的值 
		int **arc;//邻接矩阵
		int *in; //每个顶点入度的值 
};
#endif

MGraph.cpp

#include <iostream>
#include <cstring>
#include <stdlib.h>
#include <string>
using namespace std;
#include "MGraph.h"

MGRAPH::MGRAPH()
{
	int i,j;
	for(i=0;i<numNodes;++i)
	{
		vexs = new  char[numNodes];
		vexs[i]='a'+i;
		for(j=0;j<numNodes;++j)
		{
			arc[i][j]=0;
		}
	}
}
MGRAPH::~MGRAPH()
{
	delete vexs;
	for(int i=0;i<numNodes;++i)
	{
		delete arc[i];
	}
}
void MGRAPH::CreateMGraph()
{
	int i,j,k,w,numnode;
	char e;
	cout <<"输入图的种类(1-无向无权，2-有向无权，3-无向有权, 4-有向有权): ";
	cin >>kind;
	cout<<"输入顶点数: ";
	cin>>numNodes;
	numnode=numNodes+11;
	cout<<"输入边数: ";
	cin >>numEdges;//算边可能点不在范围内及自己连自己？
	vexs = new  char[numnode];
	in = new int[numnode];
	 arc = new int*[numnode];
	for(i = 0;i <numnode;i++)
	{
		arc[i]=new int[numnode];
	}
	for(i = 0;i <numnode;i++)//用此
		for(j = 0;j <numnode;j++)
		{ 
			arc[i][j]=0;	// 邻接矩阵初始化
			in[i]=0; 
		} 
	for(i = 0;i <numNodes;i++) // 读入顶点信息,建立顶点表 
	{
		cout<<"输入顶点：(点的下标为"<<i<<")\n";
		cin >> vexs[i];
	}
	for(k = 0;k <numEdges;k++) // 读入numEdges条边 
	{
		if(kind==1||kind==2)
		{
			cout<<"输入边的两点下标(如果有向注意顺序): ";
			scanf("%d %d",&i,&j);
			arc[i][j]=1;
			in[j]++;
			if(kind==1)
			{ 
				arc[j][i]=1;
				in[i]++;
			} 
	}
		else
		{
			cout<<"输入边的两点下标(如果有向注意顺序)及权: ";
			cin >> i >> j >> w;
			arc[i][j]=w;
			in[j]++;
			if(kind==3)
			{
				arc[j][i]=w;
				in[i]++;
			}
		}
	}
}
void MGRAPH::PutoutGraph() const
{
	int i,j;
	cout<<"  ";
	for(i=0;i<numNodes;++i)
	{
		cout<<vexs[i]<<' ';
	}
	cout<<endl;
	for(i=0;i<numNodes;++i)
	{
		cout<<vexs[i]<<' ';
		for(j=0;j<numNodes;++j)
		{
			cout<<arc[i][j]<<' ';
		}
		cout<<'\n';
	}
//	for(int i=0;i<numNodes;++i)
//	{
//		cout<<vexs[i]<<"的度: "<<in[i]<<endl; 
//	} 
	cout<<"图的种类: ";
	if(kind==1)
	{
		cout<<"无权无向图\n";
	}
	else if(kind==2)
	{
		cout<<"无权有向图\n";
	}
	else if(kind==3)
	{
		cout<<"有权无向图\n";
	}
	else
	{
		cout<<"有权有向图\n";
	}
	cout<<"边的条数: "<<numEdges<<endl;
	cout<<"点的个数: "<<numNodes<<endl;

}
void MGRAPH::DestoryGraph()
{
	int i,j;
	for(i = 0;i <numNodes+11;i++)
			delete	arc[i];
	delete vexs;
	delete in;
	numEdges=0;
	numNodes=0;
} 
int MGRAPH::LocateVertex( char v)
{
	int i=-1,k,ok=1;
	for(k=0;k<numNodes&&ok;++k)
	{
		if(vexs[k]==v)
		{
			i=k;
			ok=0;
		}
	}
	return i;
}
char MGRAPH::GetVertex( int i)
{
	return i > numNodes ? 0 :vexs[i-1];
}
string MGRAPH::FirstAdjVertex( char v)
{
	int i=LocateVertex(v),ok=1;
	string c;
	for(int j=0;j<numNodes&&ok;++j)
	{
		if(arc[i][j]!=0)
		{
			c=vexs[j];
			ok=0;
		}
	}
	return ok==0 ? c : "该点无邻接点";
}
string MGRAPH::NextAdjVertex(char v, char w)
{
	int i=LocateVertex(v),ok=1,okk=0;
	string c;
	for(int j=0;j<numNodes&&ok;++j)
	{
		if(okk&&arc[i][j]!=0)
		{
			c=vexs[j];
			ok=0;
		}
		if(!okk&&arc[i][j]!=0&&vexs[j]==w)
		{
			okk=1;
		}
	}
	return ok==0 ? c : "该点无邻接点";
}
void MGRAPH::InsertVertex( char v)
{
	vexs[numNodes]=v;
	numNodes++;
}
void MGRAPH::DeleteVertex( char v)
{
	int i, j=LocateVertex(v),k;
	for(i=0;i<numNodes;++i)
	{
		if(arc[j][i]!=0)
		{
			numEdges--;
		}
		if(kind==2||kind==4)
		{
			if(arc[i][j]!=0)//有向图要减两次
			{
				numEdges--;
			}
		}
		arc[j][i]=0;
		if(kind==1||kind==3)
		arc[i][j]=0;
	}
	for(k=j;k<numNodes;++k)//边也要重新，每层更新干净
	{
		for(i=0;i<numNodes;++i)
		{
			arc[k][i]=arc[k+1][i];
		}
	}
	for(k=j;k<numNodes;++k)
	{
		for(i=0;i<numNodes-1;++i)
		{
			arc[i][k]=arc[i][k+1];
		}
	}
	for(i=j;i<numNodes-1;++i)
	{
		vexs[i]=vexs[i+1];
	}
	numNodes--;
}
void MGRAPH::DeleteEdges(char v, char w)
{
	int i=LocateVertex(v),j=LocateVertex(w);
	if( i < 0 || j < 0 || i == j )//i,j不符时
		return;
	arc[i][j]=0;
	if(kind==1||kind==3)
	arc[j][i]=0;
	numEdges--;
}
void MGRAPH::InsertVertex( char v, char w)
{
	int a;
    int i=LocateVertex(v),j=LocateVertex(w);
    if(i==j)
    return ;
    if(arc[i][j]!=0)
    {
    	numEdges--;
	}
    if(kind==3||kind==4)
    {
    	cout<<"输入该边的权: ";
    	cin >> a;
    	arc[i][j]=a;
    	if(kind==3)
    	{
    		arc[j][i]=a;
		}
	}
	else
	{
	    arc[i][j]=1;
	    if(kind==1)
	    arc[j][i]=1;
	}
    numEdges++;
}

void MGRAPH::DFS(int i,bool vis[])
{
	int j;
	vis[i]=true;
	cout<<vexs[i]<< " ";
	for(j=0;j<numNodes;++j)
	{
		if(arc[i][j]!=0&&!vis[j])
		{
			DFS(j,vis);
		}
	}
}
int MGRAPH::DFSTrave()
{
	int i,s=0;
	bool vis[numNodes];
	memset(vis,false,sizeof(vis));
	for(i=0;i<numNodes;++i)
	{
		if(!vis[i])
		{
			DFS(i,vis);
			++s;//块的个数
		}
	}
	return s;
}
void MGRAPH::Floyd(int t, int t1)//t到t1的最短路径
{
	int i,j,u;
	int a[100][100];
	int **path;
	path = new int*[numNodes];
	for(i=0;i<numNodes;++i)
	{
		path[i] = new int[numNodes];
	} 
	for(i=0;i<numNodes;++i)
	{
		for(j=0;j<numNodes;++j)
		{
			if(arc[i][j]==0)
			arc[i][j]=999999;//此999999设为max 
		}
	}
	for(i=0;i<numNodes;++i)
	{
		for(j=0;j<numNodes;++j)
		{
			a[i][j]=arc[i][j];
			path[i][j]=-1;
		}
	}
	for(u=0;u<numNodes;++u)
	{
		for(i=0;i<numNodes;++i)
		{
			for(j=0;j<numNodes;++j)
			{
				if(a[i][j]>a[i][u]+a[u][j])
				{
					a[i][j]=a[i][u]+a[u][j];
					path[i][j]=u;
				}
			}
		}
	}
	if(a[t][t1]==999999)
	{
		cout<<"无路径"; 
	}
	else
	cout<<"最短路径: "<< a[t][t1]<<endl;
	FloydPrintPath(t,t1,path);
	for(i=0;i<numNodes;++i)
	{
		delete path[i];
	} 
}
void MGRAPH::FloydPrintPath(int u,int v,int **path)//输出u到v最短路径路线 
{
	if(path[u][v]==-1)
	{
		cout<<vexs[u]<<"->"<<vexs[v]<<' ';
	}
	else
	{
		int mid  = path[u][v];
		FloydPrintPath(u,mid,path);
		FloydPrintPath(mid,v,path);
	}
}
int MGRAPH::TopologicalSort()//拓扑排序 
{
	int i, k, count = 0,gettop,top = 0,top2;
	int stack[numNodes]; // 用于存储入度为0的顶点
	int etv[numNodes],stack2[numNodes]; 
	for( i=0; i < numNodes; i++ )
	{
		if( 0 == in[i] )
		{
			stack[++top] = i; // 将度为0的顶点下标入栈
		}
	}
	top2 = 0;
	for( i=0; i < numNodes; i++ )
	{
		etv[i] = 0;
	}
	
	while( 0 != top )
	{
		gettop = stack[top--]; // 出栈
		stack2[++top2] = gettop; // 保存拓扑序列顺序
		count++;
		
		for(int j=0;j<numNodes;++j)
		{
			if(arc[gettop][j]!=0)
			{
			    if( !(--in[j]) )
			    {
					stack[++top] = j;
			    }
			
			  	if( (etv[gettop]+arc[gettop][j]) > etv[j] )
			  	{
			    	etv[j] = etv[gettop] +arc[gettop][j];
			  	}
			}
		}
	}
	if( count < numNodes ) //存在环
	{
		return -1;
	}
	else
	{
		return 0;
	}
	
} 
void MGRAPH::CriticalPath()//关键路径 
{
	int i, gettop, k, j,m=0,ete, lte;
	int etv[numNodes],stack2[numNodes],top2,ltv[numNodes]; 
	int  count = 0,top = 0;
	int stack[numNodes]; // 用于存储入度为0的顶点
	
	for( i=0; i < numNodes; i++ )
	{
		if( 0 == in[i] )
		{
			stack[++top] = i; // 将度为0的顶点下标入栈
		}
	}
	top2 = 0;

	for( i=0; i < numNodes; i++ )
	{
		etv[i] = 0;
	}
	
	while( 0 != top )
	{
		gettop = stack[top--]; // 出栈
		stack2[++top2] = gettop; // 保存拓扑序列顺序
		count++;
		
		for(int j=0;j<numNodes;++j)
		{
			if(arc[gettop][j]!=0)
			{
			    if( !(--in[j]) )
			    {
					stack[++top] = j;
			    }
			
			  	if( (etv[gettop]+arc[gettop][j]) > etv[j] )
			  	{
			    	etv[j] = etv[gettop] +arc[gettop][j];
			  	}
			}
		}
	}
	if( count < numNodes ) //存在环或无向图 
	{
		cout<<"无关键路径\n";
	}
	else
	{
		for( i=0; i < numNodes; i++ )
		{
			ltv[i] =etv[numNodes-1];
		}
		while( 0 != top2 )
		{
			gettop = stack2[top2--];
			for(int j=0;j<numNodes;++j) 
			{
				if(arc[gettop][j]!=0)
				{
					if( (ltv[j] - arc[gettop][j]) < ltv[gettop] )
					{
						ltv[gettop] = ltv[j] - arc[gettop][j];
					}
				}
			}
		}
		
		for( j=0; j < numNodes; j++ )
		{
			for(int k=0; k < numNodes;++k)
			{
				if(arc[j][k]!=0)
				{
					ete = etv[j];
					lte = ltv[k] - arc[j][k];
					if( ete == lte )
					{
						cout<<vexs[j]<<"->"<<vexs[k]<<" length: "<< arc[j][k]<<" "<<endl;
						m++;
					}
				}
			}
		}
		if(!m)
		{
			cout<<"无关键路径\n";
		}

	}
	
	
	
}

子类邻接表存储
AGraph.h

#ifndef _AGraph_h_
#define _AGraph_h_
#include "Graph.h"

struct EdgeNode //* 边表结点
{ 
	int adjvex;    //* 邻接点域,存储该顶点对应的下标
	int info;		//* 用于存储权值,对于非网图可以不需要
	struct EdgeNode *next; //* 链域,指向下一个邻接点
};

 struct VertexNode //* 顶点表结点
{
	int in;//点的入度 
	char data; //* 顶点域,存储顶点信息
	EdgeNode *firstedge;//* 边表头指针
};
class AGRAPH: virtual public GRAPH
{
	public:
		AGRAPH();//构造 
		~AGRAPH();//析构
		 
		void CreateMGraph();//创建 
		void DestoryGraph();//销毁 
		void PutoutGraph() const;//输出 
		
		
		int LocateVertex( char v);//返回点的下标 
		char GetVertex( int i);//返回下标为i的点的值 
		string FirstAdjVertex( char v);//v的第一个邻接点 
		string NextAdjVertex( char v, char w);//v的w后面的邻接点 
		void InsertVertex( char v);//插入点 
		void DeleteVertex( char v);//删除点以及相关边 
		void DeleteEdges( char v, char w);//删除边 
		void InsertVertex( char v, char w);//插入两点间的边 
		
		void DFS( int i,bool vis[]);//从第i个点遍历 
		int DFSTrave();//遍历块的个数	
		
		void Floyd(int t, int t1);//两点最短路径 
		void FloydPrintPath(int u,int v,int **path);//输出路径过程 
		
		int TopologicalSort();//拓扑排序 
		void CriticalPath();//关键路径 
		 
	protected:
		VertexNode *vexs;
};
#endif

AGraph.cpp

#include <iostream>
#include <cstring>
#include <string>
#include <stdlib.h>
using namespace std;
#include "AGraph.h"

AGRAPH::AGRAPH()
{
	vexs = new VertexNode[numNodes];
	for (int i = 0; i <numNodes; i++)
    {
        vexs[i].data = 'a'+i;
        vexs[i].firstedge = NULL;
    }
}
AGRAPH:: ~AGRAPH()
{
	delete vexs;
}
void AGRAPH::CreateMGraph()
{
	int i,j,k,w;
	EdgeNode *e;
	cout<<"输入图的类型(1-无向无权，2-有向无权，3-无向有权, 4-有向有权):";
	cin>>kind;
	printf("输入顶点数和边数:\n");
	scanf("%d %d",&numNodes,&numEdges); // 输入顶点数和边数
	vexs = new VertexNode[numNodes+11];
	for(i = 0;i < numNodes;i++) //读入顶点
	{
		cout<<"输入点: ";
	 	cin>>vexs[i].data;// 输入顶点信息
		vexs[i].firstedge=NULL; 	//将边表置为空表
		vexs[i].in=0;
	}
	for(k = 0;k < numEdges;k++)// 建立边表
	{
		printf("输入边上的顶点序号:\n");
		scanf("%d %d",&i,&j); // 输入边(vi,vj)上的顶点序号 
		e = new EdgeNode; // 向内存申请空间,生成边表结点
		if(kind>2)
		{
			cout<<"输入权: ";
			cin>>w;
			e->info=w;
		}
		else
		{
			e->info=0;
		}
		e->adjvex=j;
		vexs[j].in++;
		e->next=vexs[i].firstedge;	// 将e的指针指向当前顶点上指向的结点
		vexs[i].firstedge=e;// 将当前顶点的指针指向e
		
		
		if(kind==1||kind==3)
		{
			e=new EdgeNode; //向内存申请空间,生成边表结点
			if(kind>2)
			{
				e->info=w;
			}
			else
			{
				e->info=0;
			}
			e->adjvex=i;					
			vexs[i].in++;
			e->next=vexs[j].firstedge;	
			vexs[j].firstedge=e;
		}
	}
}
void AGRAPH::PutoutGraph() const
{
	int i,j;
	EdgeNode *p;
	for(i=0;i<numNodes;++i)
	{
		j=0;
		p=vexs[i].firstedge;
		cout<<vexs[i].data<<' ';
		while(p!=NULL)
		{
			{
				cout<<vexs[i].data<<"->"<<vexs[p->adjvex].data<<" "; 
				if(kind>2)
				cout<<": "<<p->info<<' ';
			}
			p=p->next;
		}
		cout<<'\n';
	}
//	for(int i=0;i<numNodes;++i)
//	{
//		cout<<vexs[i].data<<"的度: "<<vexs[i].in<<endl; 
//	} 
	cout<<"图的种类: ";
	if(kind==1)
	{
		cout<<"无权无向图\n";
	}
	else if(kind==2)
	{
		cout<<"无权有向图\n";
	}
	else if(kind==3)
	{
		cout<<"有权无向图\n";
	}
	else
	{
		cout<<"有权有向图\n";
	}
	cout<<"点的个数: "<<numNodes<<endl;
	cout<<"边的条数: "<<numEdges<<endl;
}
void AGRAPH::DestoryGraph()
{
	int i;
	EdgeNode *p, *q;
	for(i = 0;i <numNodes;i++)
	{
		p = vexs[i].firstedge;
		while(p)
		{
			q=p->next;
			if(kind==3||kind==4)
			{
				p->info=0;
			}
			delete p;
			p=q;
		}
	}
	numEdges=0;
	numNodes=0;
}
int AGRAPH::LocateVertex(char v)
{
	int i=-1,k,ok=1;
	for(k=0;k<numNodes&&ok;++k)
	{
		if(vexs[k].data==v)
		{
			i=k;
			ok=0;
		}
	}
	return i;
}
char AGRAPH::GetVertex(int i)
{
	return i > numNodes || i<=0 ? 0 : vexs[i-1].data;
}
string AGRAPH::FirstAdjVertex(char v)
{
	EdgeNode *p;
	string c;
	int i=LocateVertex(v);
	p = vexs[i].firstedge;
	if(p)
	{
		c= vexs[p->adjvex].data;
	}
	else
	{
		c= "该点无邻接点";
	}
	return c;
}
string AGRAPH::NextAdjVertex( char v, char w)
{
	EdgeNode *p;
	string c;
	int i=LocateVertex(v),j=LocateVertex(w);
	p = vexs[i].firstedge;
	while(p && p->adjvex != j)
	{
		p=p->next;
	}
	if(!p || !p->next)
	{
		c= "该点无邻接点";
	}
	else
	{
		p=p->next;
		c= vexs[p->adjvex].data;
	}
	return c;
}
void AGRAPH::InsertVertex(char v)
{
	vexs[numNodes].data=v;
	vexs[numNodes].firstedge=NULL;
	numNodes++;
}
void AGRAPH::DeleteVertex( char v)
{
	int i, j=LocateVertex(v),k;
	EdgeNode *p, *q;//q记录新的 
	p=vexs[j].firstedge;
	cout<<"ss\n";
	while(p)
	{
		//q=p;
//		if(kind>2)
//		{
//			p->info=0;
//		} 
		delete p;
		p=p->next;
//		numEdges--;
	}
	for(i=j;i<numNodes-1;++i)
	{
		vexs[i] =vexs[i+1];
	}
	for(i=0;i<numNodes-1;++i)
	{
		p=vexs[i].firstedge;
		while(p)
		{
			if(p->adjvex == j)
			{
				if(p==vexs[i].firstedge)//如果要删除的是第一个结点 
				{
					vexs[i].firstedge=p->next;
					if(kind>2)
					{
						p->info=0;	
					}
					delete p;
					p=vexs[i].firstedge;
				} 
				else
				{
					q->next=p->next;
					if(kind>2)
					{
						p->info=0;	
					}
					delete p;
					p=p->next;
				}
				if(kind==2||kind==4)
				numEdges--; 
			}
			else
			{
				if(p->adjvex>j)
				{
					p->adjvex--;
				}
				q=p;
				p=p->next;
			}
		}
	}
	numNodes--;
}
void AGRAPH::DeleteEdges(char v, char w)
{
	EdgeNode *p,*q;
	int i=LocateVertex(v),j=LocateVertex(w);
	if( i < 0 || j < 0 || i == j )//i,j不符时
		return;
	p = vexs[i].firstedge;//p指向v的第一条弧尾
	while(p && p->adjvex!=j)
	{
		q=p;
		p=p->next;
	}
	if(p && p->adjvex == j)
	{
		if( p == vexs[i].firstedge )  
			vexs[i].firstedge = p->next;  
		else
			q->next = p->next;  
		if( kind > 2 )
			p->info=0;     
		delete p;                 
	}
	if(kind==1||kind==3)
	{
		p = vexs[j].firstedge;//p指向v的第一条弧尾
		while(p && p->adjvex!=i)
		{
			q=p;
			p=p->next;
		}
		if(p && p->adjvex == i)
		{
			if( p == vexs[j].firstedge ) 
				vexs[j].firstedge = p->next;  
			else
				q->next = p->next; 
			if( kind > 2 )
				p->info=0;      
			delete p;                   
		}
	}
	numEdges--;
}
void AGRAPH::InsertVertex( char v, char w)
{
	int a;
	EdgeNode *p;
    int i=LocateVertex(v),j=LocateVertex(w);
    if( i < 0 || j < 0 ||i==j )
   		return;
    p = new EdgeNode;
    if(kind==3||kind==4)
    {
    	cout<<"输入该边的权: ";
    	cin >> a;
    	p->info = a;
    }
    p->adjvex = j;
	p->next = vexs[i].firstedge;
	vexs[i].firstedge = p;
	if(kind==3||kind==1)
	{
		p = new EdgeNode;
		p->adjvex = i;
	    if(kind==3)
	    {
	    	p->info=a;
		}
		p->next = vexs[j].firstedge;
		vexs[j].firstedge = p;
	}
    numEdges++;
}
void AGRAPH::DFS( int i,bool vis[])
{
	EdgeNode *p;
	p=vexs[i].firstedge;
	vis[i]=true;
	cout<<vexs[i].data<< " ";
	while(p)
	{
		
		if(!vis[p->adjvex])
		{
			DFS(p->adjvex,vis);
		}
		p=p->next;
	}
}
int AGRAPH::DFSTrave()
{
	int i,s=0;
	bool vis[numNodes]; 
	memset(vis,false,sizeof(vis));
	for(i=0;i<numNodes;++i)
	{
		if(!vis[i])
		{
			DFS(i,vis);
			++s;//块的个数
		}
	}
	return s;
}
void AGRAPH::Floyd(int t, int t1)
{
	int i,j,u;
	int dis[100][100];
	int **path;
	path = new int*[numNodes];
	for(i=0;i<numNodes;++i)
	{
		path[i] = new int[numNodes];
	} 
	for(i=0;i<numNodes;++i)
	{
		for(j=0;j<numNodes;++j)
		{
			if(i==j) dis[i][j]=0;
			else dis[i][j]=999999;
		}
	}
	for(i=0;i<numNodes;++i)
	{
		for(j=0;j<numNodes;++j)
		{
			path[i][j]=-1;
		}
	}
	EdgeNode *p;
	for(i=0;i<numNodes;++i)
	{
		p=vexs[i].firstedge;
		while(p)
		{
			dis[i][p->adjvex]=p->info;
			p=p->next;
		}
	}
	for(u=0;u<numNodes;++u)
	{
		for(i=0;i<numNodes;++i)
		{
			for(j=0;j<numNodes;++j)
			{
				if(dis[i][j]>dis[i][u]+dis[u][j])
				{
					dis[i][j]=dis[i][u]+dis[u][j];
					path[i][j]=u;
				}
			}
		}
	}
	if(dis[t][t1]==999999)
	{
		cout<<"无路径"; 
	}
	else
	cout<<"最短路径: "<< dis[t][t1]<<endl;
	FloydPrintPath(t,t1,path);
	for(i=0;i<numNodes;++i)
	{
		delete path[i];
	} 
}
 void AGRAPH::FloydPrintPath(int u,int v, int **path)
 {
 	if(path[u][v]==-1)
	{
		cout<<vexs[u].data<<"->"<<vexs[v].data<<' ';
	}
	else
	{
		int mid  = path[u][v];
		FloydPrintPath(u,mid,path);
		FloydPrintPath(mid,v,path);
	}
 }
int AGRAPH::TopologicalSort()//拓扑排序 
{
	EdgeNode *e;
	int i, k, gettop;
	int top = 0; // 用于栈指针下标索引
	int count = 0; // 用于统计输出顶点的个数
	int stack[numNodes],etv[numNodes],stack2[numNodes]; // 用于存储入度为0的顶点

	
	for( i=0; i < numNodes; i++ )
	{
		if( 0 == vexs[i].in )
		{
			stack[++top] = i; // 将度为0的顶点下标入栈
		}
	}
	
	int top2 = 0;

	for( i=0; i < numNodes; i++ )
	{
		etv[i] = 0;
	}
	
	while( 0 != top )
	{
		gettop = stack[top--]; // 出栈
		stack2[++top2] = gettop;
		count++;
		
		for( e=vexs[gettop].firstedge; e; e=e->next )
		{
			k = e->adjvex;
			if( !(--vexs[k].in) )
			{
				stack[++top] = k;
			}
	
			if( (etv[gettop]+e->info) > etv[k] )
			{
				etv[k] = etv[gettop] + e->info;
			}
		}
	}
	
	if( count < numNodes ) //存在环
	{
		return -1;
	}
	else
	{
		return 0;
	}
} 

void AGRAPH::CriticalPath()//关键路径 
{
	EdgeNode *e;
	int i, gettop, k, j,top=0,count=0,ete,lte,m=0;
	int etv[numNodes], stack2[numNodes],top2,ltv[numNodes]; 
	int stack[numNodes]; // 用于存储入度为0的顶点
	
	for( i=0; i < numNodes; i++ )
	{
		if( 0 == vexs[i].in )
		{
			stack[++top] = i; // 将度为0的顶点下标入栈
		}
	}
	
	top2 = 0;

	for( i=0; i < numNodes; i++ )
	{
		etv[i] = 0;
	}
	
	while( 0 != top )
	{
		gettop = stack[top--]; // 出栈
		stack2[++top2] = gettop;
		count++;
		
		for( e=vexs[gettop].firstedge; e; e=e->next )
		{
			k = e->adjvex;
			if( !(--vexs[k].in) )
			{
				stack[++top] = k;
			}
	
			if( (etv[gettop]+e->info) > etv[k] )
			{
				etv[k] = etv[gettop] + e->info;
			}
		}
	}
	
	if( count < numNodes ) //存在环或无向图 
	{
		cout<<"无关键路径\n";
	}
	else
	{
		for( i=0; i < numNodes; i++ )
		{
			ltv[i] = etv[numNodes-1];
		}
		while( 0 != top2 )
		{
			gettop = stack2[top2--];
			for( e=vexs[gettop].firstedge; e; e=e->next )
			{
				k = e->adjvex;
				if( (ltv[k] - e->info) < ltv[gettop] )
				{
					ltv[gettop] = ltv[k] - e->info;
				}
			}
		}
		
		for( j=0; j < numNodes; j++ )
		{
			for( e=vexs[j].firstedge; e; e=e->next )
			{
				k = e->adjvex;
				ete = etv[j];
				lte = ltv[k] - e->info;
				
				if( ete == lte )
				{
					cout<<vexs[j].data<<"->"<<vexs[k].data<<" length: "<< e->info<<" "<<endl;
					m++;
				}
			}
		}
		
		if(!m)
		{
			cout<<"无关键路径\n";
		}
	}
}

main.cpp

#include <iostream>
#include <cstring>
#include <string>
using namespace std;
#include "Graph.h"
#include "MGraph.h"
#include "AGraph.h"

int main()
{ 
	int i,j,ok=1,okk=0,n,a,b;
	char c, v, w,t,t1;
	GRAPH *G;
	cout <<"1-矩阵存储 2-邻接表存储: ";
	cin >> n;
	if(n==1)
	{
		G = new MGRAPH;//矩阵 
	}
	else
	{
		G = new AGRAPH;//邻接表 
	}
	do
	{
		cout<<"G-创建 D-销毁 P-输出 I-插入点 E-插入边 B-删除点 S-删除边 L-查点 F-邻接点 N-邻接点2 T-遍历块个数 Z-最短路径 C-关键路径 Q-结束: >";
		cin >> c;
		c=toupper(c);
		if(c=='G')
		{
			G->CreateMGraph();
			okk=1;
		}
		else if(c=='D'&&okk)
		{
			G->DestoryGraph();
			okk=0;
		}
		else if(c=='P'&&okk)
		{
			G->PutoutGraph();
		}
		else if(c=='I'&&okk)
		{
			cout<<"输入要插入点的值: ";
			cin >> v;
			G->InsertVertex(v);
		}
		else if(c=='E'&&okk)
		{
			cout<<"输入要插入弧的边上的两点值: ";
			cin>>v>>w;
			a=G->LocateVertex(v);
			b=G->LocateVertex(w);
			if(a>=0&&a<G->ReturnVert()&&b>=0&&b<G->ReturnVert())
			G->InsertVertex( v, w);
			else
			cout<<"错误\n";
		}
		else if(c=='B'&&okk)
		{
			cout<<"输入要删除点的值: ";
			cin>>v;
			a=G->LocateVertex(v);
			if(a>=0&&a<G->ReturnVert())
			G->DeleteVertex( v);
			else
			cout<<"错误\n";
		}
		else if(c=='S'&&okk)
		{
			cout<<"输入要删除弧的边上的两点值: ";
			cin>>v>>w;
			a=G->LocateVertex(v);
			b=G->LocateVertex(w);
			if(a>=0&&a<G->ReturnVert()&&b>=0&&b<G->ReturnVert())
			G->DeleteEdges(v, w);
			else
			cout<<"错误\n";
		}
		else if(c=='L'&&okk)
		{
			cout<<"要查找的点:";
			cin >>v;
			a=G->LocateVertex(v);
			if(a==-1)
			{
				cout<<"查无此点";
			}
			else
			{
				cout<<a;
			}
			cout<<endl;
		}
		else if(c=='F'&&okk)
		{
			cout<<"要查找的点:";
			cin >>v;
			a=G->LocateVertex(v);
			if(a>=0&&a<G->ReturnVert())
			cout<<G->FirstAdjVertex(v)<<endl;
			else
			cout<<"查询错误\n";
		}
		else if(c=='N'&&okk)
		{
			cout<<"要查找的两点:";
			cin >>v>>w;
			a=G->LocateVertex(v);
			b=G->LocateVertex(w);
			if(a>=0&&a<G->ReturnVert()&&b>=0&&b<G->ReturnVert())
			cout<<G->NextAdjVertex(v,w)<<endl;
			else
			cout<<"查询错误\n";
		}
		else if(c=='T'&&okk)
		{
			cout<<"块的个数:" << G->DFSTrave()<<"\n";
		}
		else if(c=='Z'&&okk)
		{
			cout<<"输入查询点到哪点:";
			cin >>t>>t1; 
			a=G->LocateVertex(t);
			b=G->LocateVertex(t1);
			if(a>=0&&a<G->ReturnVert()&&b>=0&&b<G->ReturnVert())
			{
				G->Floyd(a,b);
			}
			else
			{
				cout<<"错误"; 
			}
			cout<<endl;
		} 
		else if(c=='C'&&okk)
		{
			G->CriticalPath();
		}
		else if(c=='Q')
		{
			ok=0;
		}
		else
		{
			if(!okk)
			cout<<"请先创建图: \n";
			else
			cout << "输入错误，请再输入:\n";
		}
	}
	while(ok);
	return 0;
}

图的邻接矩阵和邻接表表示

悦读